Что такое индуктивность и как она измеряется. Формулы для расчета индуктивности катушек и проводников. Как индуктивность влияет на работу электрических цепей. Области применения индуктивных элементов.

Что такое индуктивность

Индуктивность — это физическая величина, характеризующая способность проводника создавать магнитное поле при протекании через него электрического тока. Индуктивность обозначается буквой L и измеряется в генри (Гн).

Основная формула, связывающая индуктивность, магнитный поток и силу тока:

Ф = L * I

где:
Ф — магнитный поток, Вб
L — индуктивность, Гн
I — сила тока, А

Чем больше индуктивность проводника, тем большее магнитное поле он создает при протекании через него тока. Индуктивность зависит от геометрических размеров, формы и материала проводника.

Единицы измерения индуктивности

Основной единицей измерения индуктивности в системе СИ является генри (Гн). Одна генри — это индуктивность замкнутого контура, в котором при изменении силы тока на 1 ампер в секунду возникает ЭДС самоиндукции в 1 вольт.

Часто используются кратные и дольные единицы:

• миллигенри (мГн) = 10^-3 Гн
• микрогенри (мкГн) = 10^-6 Гн
• наногенри (нГн) = 10^-9 Гн
• килогенри (кГн) = 10^3 Гн

Формулы для расчета индуктивности

Индуктивность длинного соленоида

L = μ * μ0 * N^2 * S / l

где:
μ — магнитная проницаемость сердечника
μ0 — магнитная постоянная, 4π * 10^-7 Гн/м
N — число витков
S — площадь поперечного сечения
l — длина соленоида

Индуктивность тороидальной катушки

L = μ * μ0 * N^2 * h * ln(R2/R1) / 2π

где:
h — высота тороида
R1 — внутренний радиус
R2 — внешний радиус

Индуктивность прямого проводника

L = 0.002 * l * (ln(4l/d) — 1)

где:
l — длина проводника
d — диаметр проводника

Как индуктивность влияет на работу электрических цепей

Индуктивность оказывает существенное влияние на работу электрических цепей, особенно при протекании переменного тока:

• Создает индуктивное сопротивление, препятствующее изменению тока
• Вызывает сдвиг фаз между током и напряжением
• Накапливает энергию в магнитном поле
• Создает ЭДС самоиндукции при изменении тока

Индуктивное сопротивление катушки зависит от частоты переменного тока:

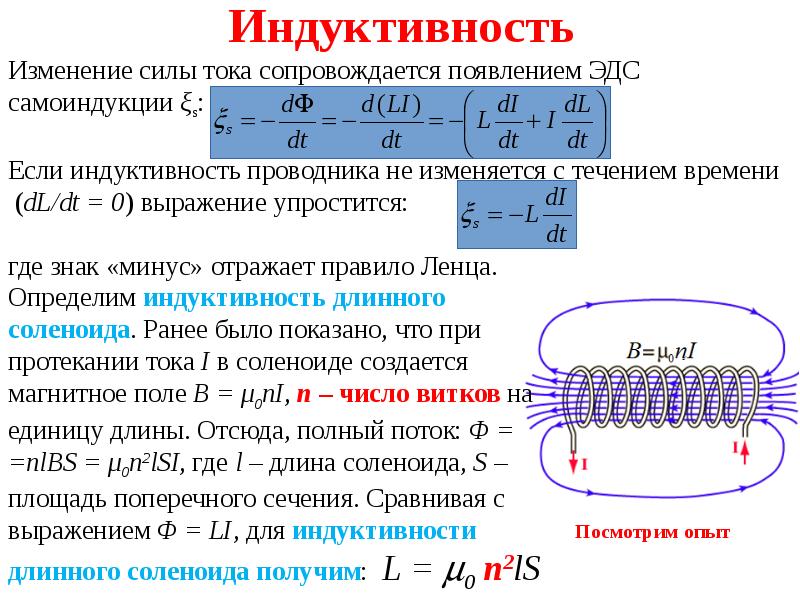
X_L = 2π * f * L

где:
X_L — индуктивное сопротивление
f — частота тока
L — индуктивность

Области применения индуктивных элементов

Индуктивные элементы широко применяются в различных областях электротехники и электроники:

• Дроссели в блоках питания для сглаживания пульсаций
• Катушки индуктивности в колебательных контурах
• Трансформаторы для преобразования напряжения
• Электромагнитные реле
• Индуктивные датчики
• Индукционные нагреватели
• Фильтры высоких и низких частот

Как измерить индуктивность

Для измерения индуктивности катушек и других элементов используются специальные приборы — измерители индуктивности (LCR-метры). Они позволяют с высокой точностью определить индуктивность в широком диапазоне значений.

Основные методы измерения индуктивности:

• Мостовой метод
• Резонансный метод
• Метод вольтметра-амперметра
• Метод сравнения

При отсутствии специальных приборов можно приближенно оценить индуктивность по геометрическим размерам катушки с помощью расчетных формул.

Маркировка индуктивных элементов

На корпусах катушек индуктивности часто наносится цветовая или цифровая маркировка, позволяющая определить номинальное значение индуктивности:

• Цветовая маркировка аналогична маркировке резисторов
• Цифровая маркировка: первые две цифры — значащие, третья — множитель
• Буквенное обозначение единиц: uH — микрогенри, mH — миллигенри

Пример маркировки: 102K — индуктивность 1000 мкГн с допуском ±10%

Последовательное и параллельное соединение индуктивностей

Последовательное соединение

При последовательном соединении катушек их общая индуктивность равна сумме индуктивностей отдельных катушек:

L = L1 + L2 + L3 + …

Параллельное соединение

При параллельном соединении катушек обратная величина общей индуктивности равна сумме обратных величин индуктивностей отдельных катушек:

1/L = 1/L1 + 1/L2 + 1/L3 + …

Как индуктивность влияет на переходные процессы в цепях

Наличие индуктивности в электрической цепи приводит к возникновению переходных процессов при коммутации:

• При включении тока в цепи с индуктивностью ток нарастает не мгновенно, а постепенно
• При отключении тока возникает ЭДС самоиндукции, стремящаяся поддержать ток
• Длительность переходного процесса зависит от величины индуктивности и активного сопротивления цепи

Постоянная времени цепи с индуктивностью:

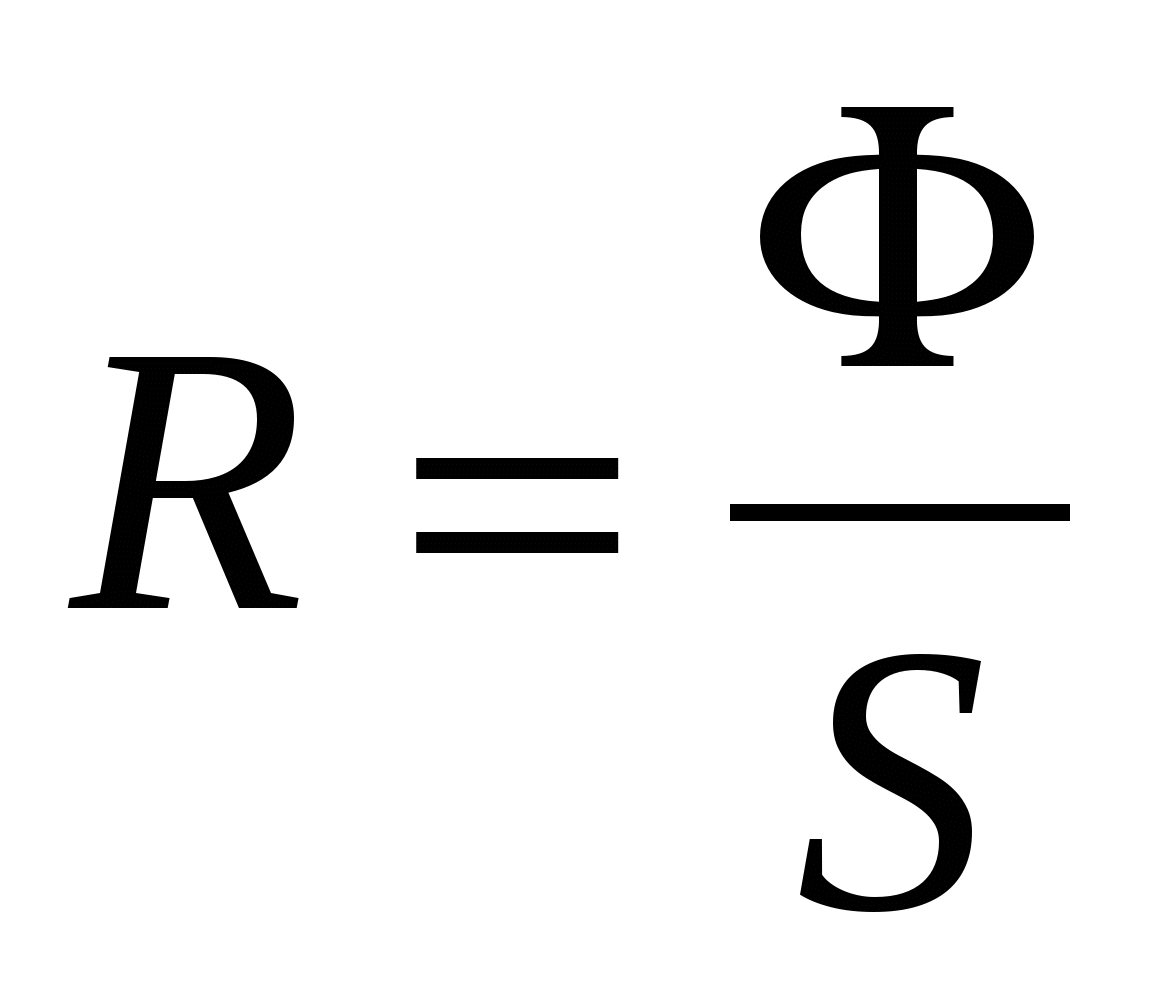
τ = L / R

где:
τ — постоянная времени
L — индуктивность
R — активное сопротивление

Заключение

Индуктивность играет важную роль в работе многих электротехнических устройств. Понимание свойств и особенностей индуктивных элементов позволяет эффективно проектировать и анализировать электрические цепи. При расчетах следует учитывать влияние индуктивности на переходные процессы и частотные характеристики цепей.

Катушка индуктивности | Виды катушек, практические опыты

Что такое катушка индуктивности

Что вы себе представляете под словом “катушка” ? Ну… это, наверное, какая-нибудь “фиговинка”, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.

Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!

Индуктивность

Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC – метра.

Что такое индуктивность?  Если через  провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:

где

В – магнитное поле, Вб

I – сила тока, А

А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение

И у нас получится вот такая картина с магнитными силовыми линиями:

Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с  Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:

С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

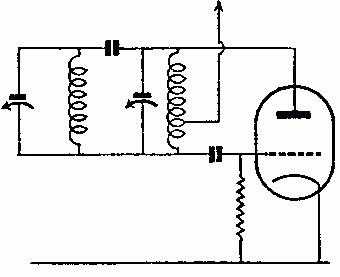
где

I – сила тока в катушке , А 

U – напряжение в катушке, В 

 R – сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Типы катушек индуктивности

Катушки индуктивности делятся в основном на два класса: с магнитным и  немагнитным сердечником. Снизу  на фото катушка с немагнитным сердечником.

Но где у нее сердечник? Воздух – это немагнитный сердечник :-).  Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным  сердечником используется, когда индуктивность не превышает 5 миллигенри.

А вот катушки индуктивности с сердечником:

В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.

Для катушек средней индуктивности используются ферритовые сердечники:

Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.

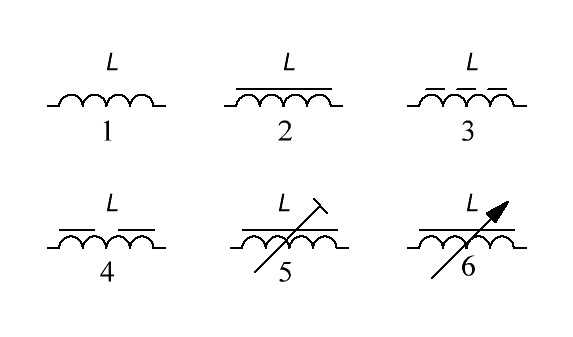
Дроссели

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Опыты с катушкой

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов.  Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр  показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине.  Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности  в переменных катушках индуктивности:

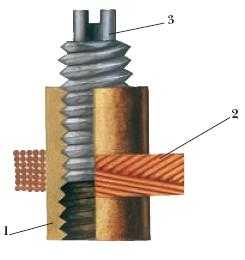
где

1 – это каркас катушки

2 – это витки катушки

3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз.  Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка  не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков  в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Обозначение на схемах

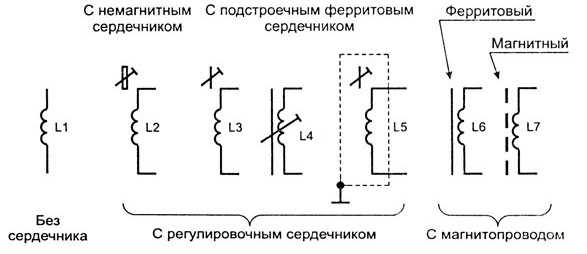
Последовательное и параллельное соединение катушек

При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.

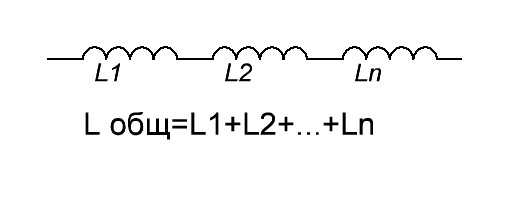
А при параллельном соединении получаем вот так:

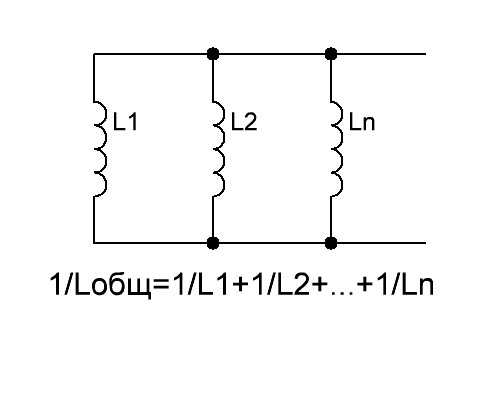
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек.  Это может привести к неправильным показаниям общей индуктивности.

Резюме

Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.

Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:

www.ruselectronic.com

Цветовая и кодовая маркировка индуктивностей

Цветовая и кодовая маркировка индуктивностей

   В соответствии с Публикацией IEC 62 для индуктивностей кодируется номинальное значение индуктивности и допуск, т.е. допускаемое отклонение от указанного номинала. Наиболее часто применяется кодировка 4 или 3 цветными кольцами или точками. Первые две метки указывают на значение номинальной индуктивности в микрогенри (мкГн), третья метка — множитель, четвертая — допуск. В случае кодирования 3 метками подразумевается допуск 20%. Цветное кольцо, обозначающее первую цифру номинала, может быть шире, чем все остальные.

Рис. 2

Таблица 1

Серебряный			0,01	10%
Золотой			0,1	5%
Черный		0	1	20%
Коричневый	1	1	10	Допуск
Красный	2	2	100
Оранжевый	3		1000
Желтый	4	4	Множитель
Зеленый	5	5
Голубой
Фиолетовый	7	7
Серый	8	8
Белый	9	9

Рис. 2

Кодовая маркировка

   Обычно для индуктивностей кодируется номинальное значение индуктивности и допуск, т.е. допускаемое отклонение от указанного номинала. Номинальное значение кодируется цифрами, а допуск — буквами. Применяется два вида кодирования.

А. Кодированная маркировка

   Первые две цифры указывают значение в микрогенри (мкГн), последняя — количество нулей. Следующая за цифрами буква указывает на допуск. Например, код 101J обозначает 100 мкГн ±5%. Если последняя буква не указывается —допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.

Допуск:

   D=±0,3 нГн; J=±5%; К=±10%; M=±20%

Примеры обозначений:

Таблица 2

Код	Обозначение
22N	22 нГн ±20%
R10M	0,10 мкГн±20%
R15M	0,15 мкГн±20%
R22M	0,22 мкГн ±20%
R33M	0,33мкГн+20%
R47M	0,47мкГн±20%
R68M	0,68 мкГн +20%
1R0M	1,2мкГн ±20%

Таблица 3

Код	Обозначение
2R2K	2,2 мкГн±10%
3R3K	3,3 мкГн ±10%
4R7K	4,7 мкГн±10%
6R8K	6,8 мкГн±10%
100К	10 мкГн±10%
150К	15 мкГн±10%
220К	22 мкГн±10%
33ОК	33 мкГн±10%

Таблица 4

Код	Обозначение
680К	68 мкГн ± 10%
101К	100мкГн±10%
151К	150 мкГн ± 10%
221K	220 мкГн ±10%
331К	33ОмкГн ±10%
471J	470 мкГн ±5%
681J	680 мкГн ±5%
102	1000 мкГн±20%

Рис. 3

В. Непосредственная маркировка

   Индуктивности маркируются непосредственно в микрогенри (мкГн). В таких случаях маркировка 680К будет означать не 68 мкГн ±10%, как в случае А, а 680 мкГн ±10%.

cxem.net

Индуктивность

Радиодеталь под названием индуктивность представляет собой простой провод, скрученный в виде спирали или мотка. Поэтому ее часто называют катушкой индуктивности или просто катушкой. Катушки обычно многослойные (то есть провод уложен в несколько слоев), и намотаны на специальный сердечник, который усиливает ее индуктивные свойства.

Рисунок 32. Внешний вид катушек индуктивности

 

Для постоянного тока катушка является обычным проводником, обладающим только сопротивлением. Однако, совсем по другому через катушку будет проходить ток переменный. Катушка, образно говоря, препятствует любому изменению тока: если ток нарастает, индуктивность будет мешать увеличению тока, а если ток уменьшается — будет стремиться ток сохранить. Понять как работает индуктивность можно на простом примере инерции. Пробуем толкнуть не заведенный автомобиль — это потребует приложения некоторых усилий, так как автомобиль обладает большой массой. Однако, для того, чтобы остановить уже разогнавшийся автомобиль потребуется приложение немалых усилий.

 

Катушка индуктивности обладает двумя параметрами, на которые следует обратить внимание — это собственно индуктивность, которая измеряется в Генри, и допустимый ток.

12. Единицы индуктивности

• 1 мГн (один миллигенри) = 0,001 Гн (одна тысячная генри)
• 1 мкГн (один микрогенри) = 0,000 001 Гн (одна миллионная генри)

От величины индуктивности зависит то, насколько сильно катушка будет сопротивляться изменению тока: чем этот параметр больше, тем сложнее переменному току «преодолеть» катушку, а потом сложнее «остановиться».

 

На этот параметр оказывают влияние многие факторы: это и количество витков в катушке, и ее диаметр, и размеры, и материал сердечника. На некоторых катушках индуктивности предусмотрена возможность регулировки, для чего сердечник может перемещаться вдоль ее оси.

 

Рисунок 33. Катушка индуктивности с подстройкой

 

Величина индуктивности, как правило, наносится на корпус катушки либо в виде цифробуквенной маркировки, либо в виде цветных полос или точек.

 

Первые две цифры указывают значение в микрогенри (мкГн, рН), последняя — количество нулей. Следующая за цифрами буква указывает на допуск (насколько реальная индуктивность может отличаться от указанной в маркировке цифры). Например, код 101J обозначает 100 мкГн с допуском ±5%. Если последняя буква не указывается — допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.

 

Допуск может обозначаться также другими буквами: D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%. Иногда катушки индуктивности маркируются непосредственно в микрогенри.

 

Цветовая маркировка катушек индуктивностей аналогична маркировке «полосатых» резисторов:

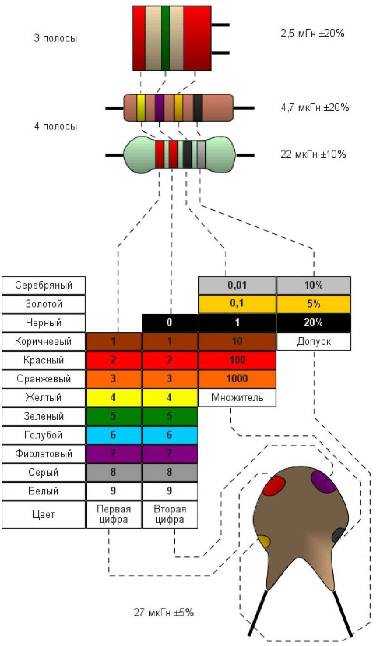
Рисунок 34. Расшифровка обозначения катушек индуктивностей

 

Допустимый ток катушки определяется в основном диаметром провода, из которого она изготовлена.

Рисунок 35. Условное изображение катушки индуктивности

 

Для переменного тока полное сопротивление катушки индуктивности зависит и от его частоты. Чем выше частота, тем меньше остается времени на преодоление током индуктивного препятствия. Значит, тем меньше тока катушка пропустит Это свойство часто используется в так называемых фильтрах — элементах, отделяющих переменный ток одной частоты от переменного же тока, но другой частоты или диапазона частот

 

Рисунок 36. Отсечение частот индуктивным фильтром

 

Аналогичным образом катушка индуктивности ведет себя не только при переменном токе, но и в момент включения или выключения постоянного. В эти моменты ток постепенно увеличивается с нуля до максимального значения (или уменьшается от максимального значения до нуля), этим он похож на переменный ток. Поэтому зачастую мощные катушки индуктивности (их иногда называют дроссели) устанавливаются на входах питания каких-либо устройств для сглаживания возможных пульсаций тока и защиты оборудования.

 

В автомобильном электрооборудовании катушки применяются очень широко, например, в катушках зажигания, акустических динамиках, электродвигателях и других устройствах.

instalator.ru

Индуктивность — это… Что такое Индуктивность?

        физическая величина, характеризующая магнитные свойства электрической цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пространстве магнитное поле, причём Магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо пропорционален силе тока I :                  Коэффициент пропорциональности L называется И. или коэффициентом самоиндукции контура. И. зависит от размеров и формы контура, а также от магнитной проницаемости (См. Магнитная проницаемость) окружающей среды. В Международной системе единиц (См. Международная система единиц) (СИ) И. измеряется в Генри, в СГС системе единиц (См. СГС система единиц) (Гаусса) И. имеет размерность длины и поэтому единица И. называется сантиметром (1 гн = 10⁹ см).          Через И. выражается эдс самоиндукции (См. Самоиндукция) в контуре, возникающая при изменении в нём тока:         

        (ΔI — изменение тока за время Δt). При заданной силе тока И. определяет энергию W магнитного поля тока:

        

        Чем больше И., тем больше магнитная энергия, накапливаемая в пространстве вокруг контура с током. Если провести аналогию между электрическими и механическими явлениями, то магнитную энергию следует сопоставить с кинетической энергией тела Т = mv²/2 (где m — масса тела, v — скорость его движения), при этом И. будет играть роль массы, а ток — роль скорости. Таким образом, И. определяет инерционные свойства тока.

         Практически участки цепи со значительной И. выполняют в виде индуктивности катушек (См. Индуктивности катушка). Для увеличения L применяют катушки с железными сердечниками, но в этом случае, в силу зависимости магнитной проницаемости μ ферромагнетиков (См. Ферромагнетики) от напряжённости поля, а следовательно, и от силы тока, И. становится зависящей от I. И. длинного соленоида из N витков, имеющего площадь поперечного сечения S и длину l, в среде с магнитной проницаемостью μ равна (в единицах СИ): L = μμ₀N ²S/l, где μ₀ — Магнитная постоянная, или магнитная проницаемость вакуума.

         Лит.: Калашников С. Г., Электричество, М., 1970 (Общий курс физики, т. 2), гл. 9.

         Г. Я. Мякишев.

dic.academic.ru

Индуктивность контура, соленоида. Катушка. Параллельное и последовательное подключение

Индуктивность контура — это коэффициент пропорциональности между постоянным током, текущим в заданном замкнутом контуре, и потоком вектора магнитной индукции, создаваемым этим током через поверхность, окружённой этим контуром. Обозначение —

, размерность — Гн (генри). Формульно:

Ф

(1)

• где
  • Ф — поток вектора магнитной индукции,
  • — индуктивность контура,
  • — сила тока в контуре.

Рис. 1. Соленоид

В большинстве задач данный параметр задан в условии, однако есть одна система, в которой данный параметр является расчётным. Это соленоид (рис. 1). Соленоидом называется провод, согнутый в виде спирали (он же, в принципе, катушка индуктивности). Формульно:

(1)

Немного о

— относительной магнитной проницаемости среды. Чаще всего в школьных задачах соленоид пустотелый, т.е. внутри него (витков) воздух, тогда . Иногда в него помещают сердечник, т.е. болванку формой повторяющую внутреннюю геометрию соленоида, тогда  и по веществу, из которого состоит сердечник, можно в таблицах найти значение магнитной проницаемости.

Для ряда задач существует всё тот же вопрос о параллельном и последовательном соединении индуктивностей. Будем считать, что взаимной индукции нет (т.е. один контур экранирован от второго). Тогда:

• при параллельном подключении:

(2)

• где
  • — общая индуктивность системы контуров,
  • — сумма обратных индуктивностей, входящих в цепь.

В случае двух элементов, соединённых параллельно:

(3)

• при последовательном подключении:

(4)

• где
  • — общая индуктивность системы контуров,
  • — сумма индуктивностей, входящих в цепь.

Поделиться ссылкой:

www.abitur.by

Генри (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Генри.

Ге́нри (русское обозначение: Гн; международное: H) — единица индуктивности в Международной системе единиц (СИ). Цепь имеет индуктивность 1 Гн, если изменение тока со скоростью один ампер в секунду создаёт ЭДС индукции, равную одному вольту.

Через другие единицы измерения СИ генри выражается следующим образом:

Гн = В·с·А⁻¹= кг·м²·с⁻²·А⁻²

Единица названа в честь американского учёного Джозефа Генри. В Международную систему единиц (СИ) генри введён решением XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием системы СИ в целом^[1]. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы генри пишется со строчной буквы, а её обозначение «Гн» — с заглавной.

Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 Гн	декагенри	даГн	daH	10−1 Гн	децигенри	дГн	dH
102 Гн	гектогенри	гГн	hH	10−2 Гн	сантигенри	сГн	cH
103 Гн	килогенри	кГн	kH	10−3 Гн	миллигенри	мГн	mH
106 Гн	мегагенри	МГн	MH	10−6 Гн	микрогенри	мкГн	µH
109 Гн	гигагенри	ГГн	GH	10−9 Гн	наногенри	нГн	nH
1012 Гн	терагенри	ТГн	TH	10−12 Гн	пикогенри	пГн	pH
1015 Гн	петагенри	ПГн	PH	10−15 Гн	фемтогенри	фГн	fH
1018 Гн	эксагенри	ЭГн	EH	10−18 Гн	аттогенри	аГн	aH
1021 Гн	зеттагенри	ЗГн	ZH	10−21 Гн	зептогенри	зГн	zH
1024 Гн	иоттагенри	ИГн	YH	10−24 Гн	иоктогенри	иГн	yH
применять не рекомендуется

ru.wikipedia.org

что такое в Физической энциклопедии

в электродинамике (коэффициент самоиндукции) (от лат. inductio — наведение, побуждение) — параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин «И.» употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним — катушка самоиндукции).И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновениювихревого электрич. поля E(r, t )с отличной от нуля циркуляцией

по замкнутым контурам l_i;пронизываемым магн. потоком Ф _i. Внутри проводника вихревое поле Е взаимодействует с порождающим его током и оказывает противодействие изменению магн. потока (Ленца правило). Циркуляция E_i и магн. поток Ф _i существенно зависят от выбора контура l_i внутри проводника конечной толщины. Однако при медленных движениях и квазистацнонарных процессах, когда полный ток

(j — плотностьтока) одинаков для всех нормальных сечений провода S _пр, допустим переход к усреднённым характеристикам: эдс самоиндукции E _си=<E_i> )и сцепленному с проводящим контуром магн. потоку Ф=_i>_. В предположении о том, что линии тока замыкаются сами на себя при одном обходе по контуру,

где r_^ , — радиус-векторы точек нормального сечения провода, Ф _j(r_^) — магн. поток через поверхность, ограниченную линией тока, проходящей через точку r_^, E_j(r_^) — циркуляция вектора E вдоль этой линии тока, j_n — нормальная к S_np составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должнаудовлетворять энергетич. соотношению: =E _сиI ( Р— суммарная мощность взаимодействия поля с током).Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:

Ф=L.I (в СИ), Ф=¹/_c(LI)(в системе СГС). (1)

Коэф. L и Lназ. И. Величина L измеряется в генри, L — в см.

E _си=-d/dt(LI) (в СИ), E_cи⁼-(1/с ²)(d/dt)(LI)(2) (в системе СГС).

Производная по времени от И. определяет ту часть E _си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.

W^m=¹/₂LI² (в СИ), W^m=¹/₂c²LI² (в системе СГС). (3)

Соотношение (3) позволяет различать И. внутреннюю L_i, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю L_e, связанную с внеш. магн. полем (L=L_i+L_e, L=L_i+L_e). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусамиих изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения L_i=(m₀/8p)m_il (l — длина провода, m_i — магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l₁) совпадает с осевой линией проводника, а другая (l₂) совмещена с его поверхностью:

где r₁, r₂ — радиус-векторы точек на контурах l_l,<sub>l2,m е — магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L «(m0/4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:

где l и а — длина и радиус провода. Это выражение обладает логарифмич. точностью — его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.

Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m0R(ln(8R/r)-2+¹/4mi), Гн, r<</sub>

Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой — соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеальногосоленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j _пов=Ik (I — ток в соленоиде, k — число витков на единице длины).

Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл.-магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока I_w и эдс самоиндукции E_w связаны соотношением:

И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление R_L(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса — Кронига соотношением:

где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением R_L(w) можно пренебречь, тогда E_w и I_w сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду:

где W^m_w— усреднённая по периоду колебаний энергия ближних (квазистационарных) магн. полей (полная магн. энергия поля не определена из-за линейно растущей во времени энергии поля излучения).Если в цепи действует гармонич. сторонняя эдс , то во втором законе Кирхгофа величина E_w может быть перенесена (со сменой знака) в правую часть равенства:

где С —ёмкость, включённая в цепь. Соотношение (9) позволяет трактовать величину Z_L=iwLкак индуктивную часть импеданса цепи (при атом Z_C=-i/w С —ёмкостная, a Z_R=R— активная части полного импеданса Z=Z_L+Z_C+Z_R). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении , а при параллельном При описании сильноточных цепей часто требуется обобщение понятия И. на случай нелинейных систем. Если неподвижный проводящий контур помещён всреду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна:

Величина L _Д(I)=d Ф /dIназ. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид:

B линейном приближении (при I «0) L _Д «L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е., Основы теории электричества9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.Главный редактор А. М. Прохоров.1988.

rus-physical-enc.slovaronline.com