Как правильно подключить ваттметр в цепь постоянного и переменного тока. Какие существуют схемы включения ваттметра. Как измерить мощность при токе нагрузки больше допустимого для прибора. На что обратить внимание при подключении ваттметра.
Принцип работы и устройство ваттметра
Ваттметр — это электроизмерительный прибор для измерения активной мощности в цепях постоянного и переменного тока. Принцип его работы основан на взаимодействии магнитных полей двух катушек:
- Токовой катушки, включаемой последовательно в измеряемую цепь
- Катушки напряжения, подключаемой параллельно нагрузке
Вращающий момент, действующий на подвижную часть прибора, пропорционален произведению тока и напряжения, то есть активной мощности. Шкала ваттметра проградуирована непосредственно в ваттах.
Схемы включения ваттметра в цепь постоянного тока
При измерении мощности в цепи постоянного тока возможны две схемы включения ваттметра:
1. Токовая обмотка до катушки напряжения
В этой схеме токовая обмотка ваттметра включается до параллельной цепи:
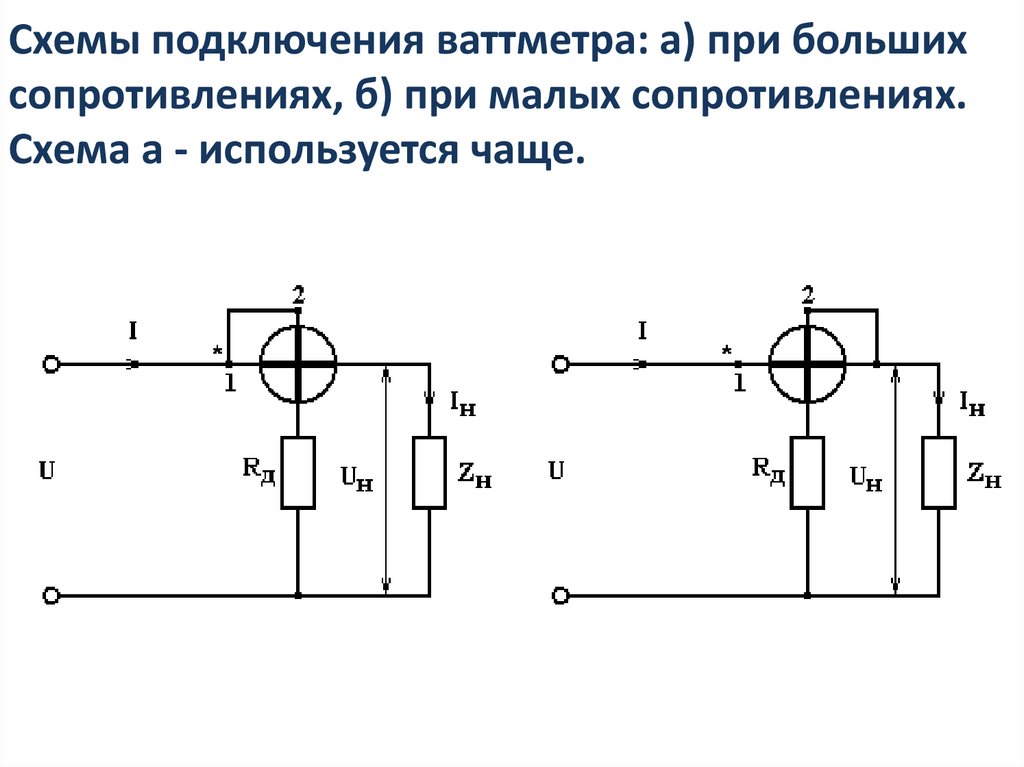
- Достоинство: меньшая погрешность из-за меньшей мощности, потребляемой параллельной цепью ваттметра
- Недостаток: завышенные показания на величину мощности, потребляемой параллельной цепью
2. Токовая обмотка после катушки напряжения
Токовая обмотка включается после параллельной цепи:
- Достоинство: измеряется только мощность нагрузки
- Недостаток: бóльшая погрешность из-за протекания дополнительного тока через токовую обмотку
При точных измерениях необходимо учитывать поправку на мощность, потребляемую параллельной цепью ваттметра.
Особенности включения ваттметра в цепь переменного тока
При измерении мощности в цепи переменного тока необходимо учитывать следующие особенности:
- Ваттметр измеряет только активную мощность
- Показания не зависят от частоты тока (в пределах рабочего диапазона прибора)
- Необходимо соблюдать правильность подключения генераторных зажимов
- В трехфазных цепях используются специальные схемы включения
Генераторные зажимы ваттметра (обозначаются *) должны быть подключены к источнику питания. При неправильном подключении стрелка прибора будет отклоняться в обратную сторону.
Измерение мощности при больших токах нагрузки
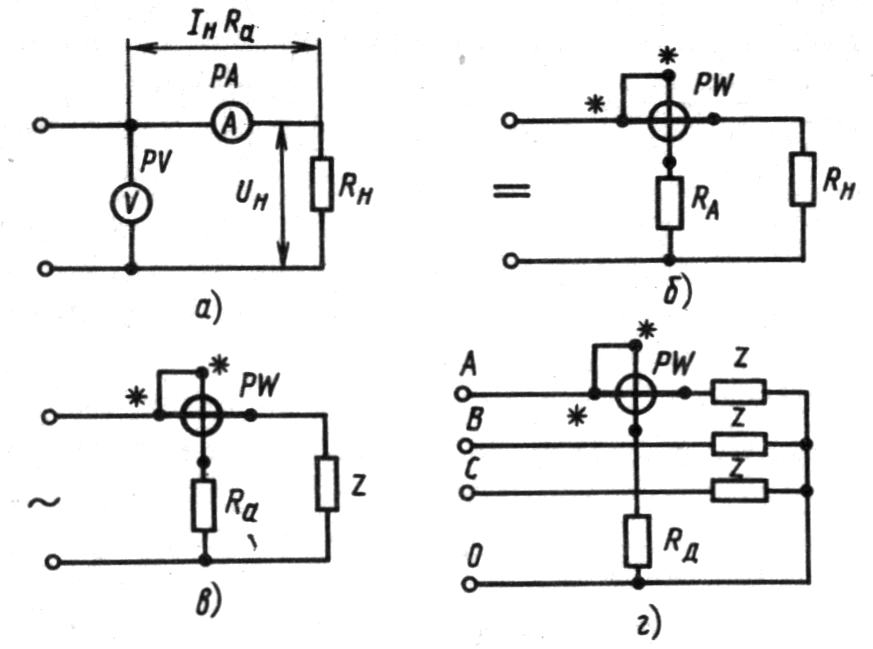
Если ток в измеряемой цепи превышает предельно допустимый ток токовой обмотки ваттметра, применяют следующие способы:
1. Использование измерительных трансформаторов тока
Схема подключения:
- Первичная обмотка трансформатора тока включается последовательно в измеряемую цепь
- Токовая обмотка ваттметра подключается ко вторичной обмотке трансформатора
- Катушка напряжения подключается через трансформатор напряжения
Показания ваттметра умножаются на коэффициенты трансформации трансформаторов тока и напряжения.
2. Применение шунтов
Параллельно токовой обмотке ваттметра подключается шунт, рассчитанный на нужный ток. Показания умножаются на коэффициент шунтирования.
Основные правила подключения ваттметра
При включении ваттметра в измеряемую цепь необходимо соблюдать следующие правила:
- Строго соблюдать полярность подключения (генераторные зажимы к источнику)
- Не превышать допустимых значений тока и напряжения для обмоток прибора
- При больших токах использовать трансформаторы тока или шунты
- В цепях переменного тока учитывать cos φ нагрузки
- При точных измерениях вносить поправку на мощность, потребляемую прибором
Правильное подключение ваттметра позволяет получить достоверные результаты измерения мощности в электрических цепях.
Измерение мощности в трехфазных цепях
Для измерения мощности в трехфазных цепях применяют следующие методы:
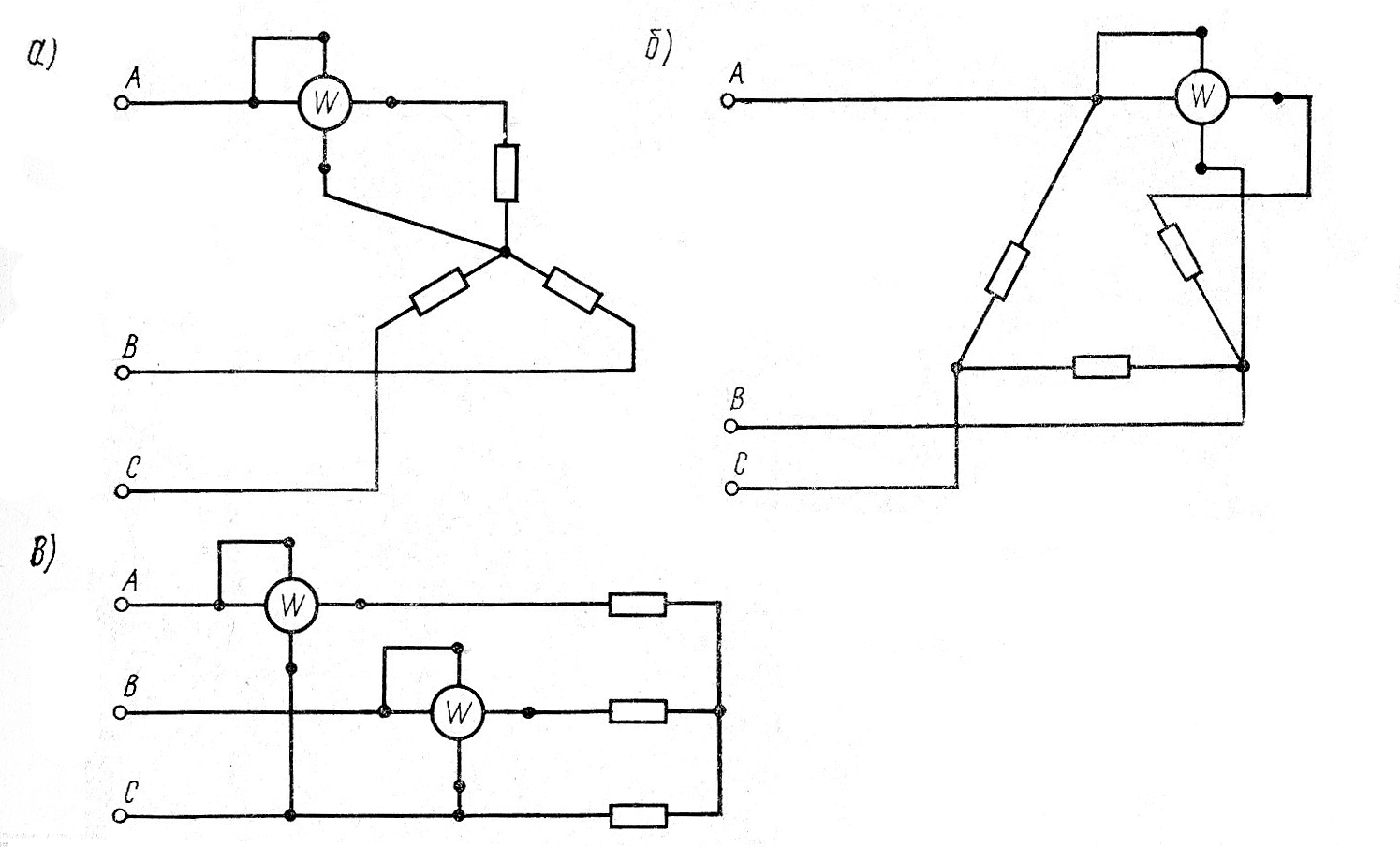
1. Метод одного ваттметра
Применяется в симметричных трехфазных цепях. Ваттметр включают в одну фазу, а общую мощность определяют умножением показаний на 3.
2. Метод двух ваттметров
Позволяет измерить мощность в трехпроводных трехфазных цепях при любой нагрузке. Токовые обмотки ваттметров включают в две фазы, а обмотки напряжения — на линейные напряжения.
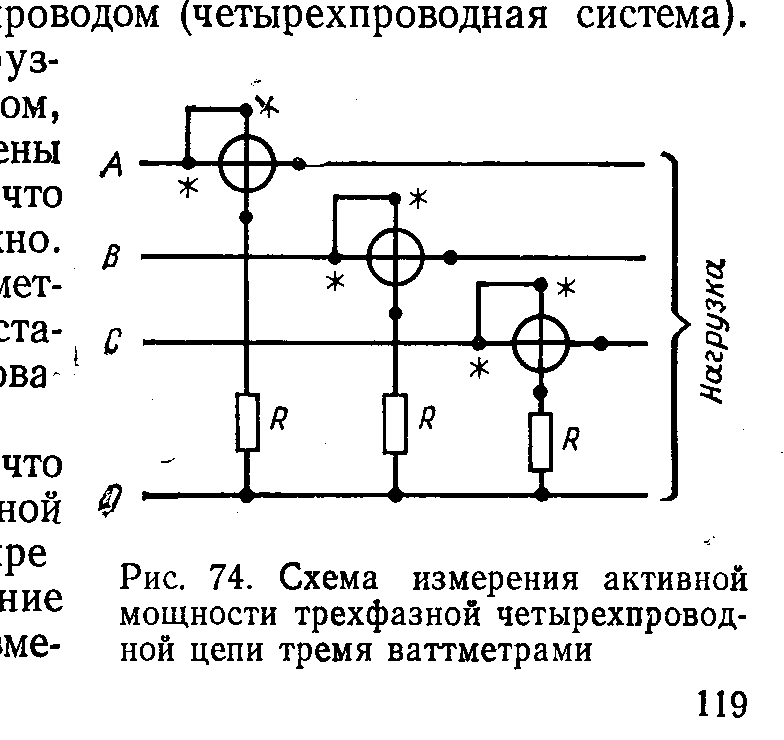
3. Метод трех ваттметров
Применяется в четырехпроводных трехфазных цепях. Каждый ваттметр измеряет мощность своей фазы. Общая мощность равна сумме показаний трех приборов.
Выбор конкретной схемы включения ваттметров зависит от схемы трехфазной цепи, характера нагрузки и требуемой точности измерений.
Цифровые ваттметры: особенности подключения
Современные цифровые ваттметры имеют ряд преимуществ по сравнению с аналоговыми приборами:
- Высокая точность измерений
- Широкий диапазон измеряемых величин
- Возможность измерения дополнительных параметров (cos φ, частота и др.)
- Автоматический выбор пределов измерения
- Возможность подключения к компьютеру для регистрации данных
При подключении цифровых ваттметров следует учитывать:
- Необходимость внешнего питания прибора
- Возможность гальванической развязки измерительных цепей
- Наличие специальных входов для подключения трансформаторов тока и напряжения
- Возможность удаленного считывания показаний
Цифровые ваттметры значительно расширяют возможности измерения мощности в современных электроустановках.
Схема — включение — ваттметр
Схема — включение — ваттметр
Cтраница 4
Отклонения стрелок ваттметра пропорциональны косинусам углов а и р, не равных углу ф, что вытекает из схемы включения ваттметров. Действительно, токовая катушка первого ваттметра включена в провод фазы А, и через нее проходит ток / д, а катушка напряжения включена на напряжение UAB. То же самое относится и ко второму ваттметру. [46]
В этом случае количество реактивной энергии подсчитывается по показаниям счетчиков по формулам, приведенным для вычисления реактивной мощности и соответствующих схемам включения ваттметров. [48]
Стрелка первого ваттметра должна отклониться в обратную сторону — не по шкале Чтобы измерить мощность, отдаваемую первой катушкой, надо изменить схему включения ваттметра Wj. Можно, например, изменить у него подключение цепи напряжения, присоединив зажим со звездочкой к нижнему проводу, а зажим без звездочки к верхнему проводу, так как это показано на рис. 6 — 17, б Тогда он будет измерять мощность, отдаваемую катушкой. [49]
Наиболее простым и точным способом измерения угла сдвига фаз между током и напряжением в однофазном токе является измерение при помощи фазометра, схема включения которого вполне аналогична со
Так как счетчик по своему устройству отличается от ваттметра только механической схемой, а вращающий момент в обоих приборах должен быть пропорционален мощности, то схема включения счетчика ничем не отличается от схемы включения ваттметра. [51]
Как видно из схемы, последовательные обмотки ваттметров включены на линейные токи, а параллельные обмо тки — на линейные напряжения. Схема включения ваттметров остается такой же и при соединении нагрузки треугольником. [52]
Более просто мощность в цепях постоянного тока измеряется с помощью электродинамического ваттметра. Схема включения ваттметра в цепь показана на рис. 6.3. Как следует из § 3.3, электродинамический стрелочный механизм имеет две обмотки. Показание ваттметра ( положительное или отрицательное) зависит от направления тока в обмотках катушек. Выводы, обозначенные этим знаком, называются генераторными выводами или генераторными зажимами. [53]
Метод трех приборов применяется для измерения активной мощности в трехфазной четырехпро-водной цепи. Схема включения ваттметров показана на рис. 5.14. По этой же схеме производится включение трехэлементных трехфазных ваттметров. [55]
Схема включения двух ваттметров в трехфазную цепь приведена на рис. 7.20. В данном случае фазы нагрузки соединены звездой. Схема включения ваттметров остается такой же и при включении нагрузки треугольником. В обоих случаях через последовательные обмотки ваттметров протекают линейные токи, а параллельные обмотки включены на линейные напряжения. Свободной фазой может быть любая из трех. [56]
Другие концы катушек напряжения присоединяют к той фазе, в которую не включены токовые катушки. При такой схеме включения ваттметра мощность, потребляемая установкой, будет равна алгебраической сумме показаний двух ваттметров. [57]
На рис. 12 14, а показано ( сплошными линиями) включение трех ваттметров PW1 — PW3 для измерения реактивной мощности в трехфазной четырехпроводной цепи. Для удобства анализа схемы включения ваттметров для измерения реактивной мощности на этом же рисунке показано включение трех ваттметров ( штриховые линии) для измерения активной мощности. [59]
Страницы: 1 2 3 4
Схема включения ваттметра
Для непосредственного измерения мощности цепи постоянного тока применяется ваттметр. Неподвижная последовательная катушка или катушка тока ваттметра соединяется последовательно с приемниками электрической энергии. Подвижная параллельная катушка или катушка напряжения, соединенная последовательно с добавочным сопротивлением, образует параллельную цепь ваттметра, которая присоединяется параллельно приемникам энергии. Так как в результате применения добавочного сопротивления параллельная цепь ваттметра имеет …
Для непосредственного измерения мощности цепи постоянного тока применяется ваттметр. Неподвижная последовательная катушка или катушка тока ваттметра соединяется последовательно с приемниками электрической энергии. Подвижная параллельная катушка или катушка напряжения, соединенная последовательно с добавочным сопротивлением, образует параллельную цепь ваттметра, которая присоединяется параллельно приемникам энергии.
Угол поворота подвижной части ваттметра:
= k2IIu = k2U/Ru
где I — ток последовательной катушки; Iи — ток параллельной катушки ваттметра.
Рис. 1. Схема устройства и соединений ваттметра
Так как в результате применения добавочного сопротивления параллельная цепь ваттметра имеет практически постоянное сопротивление ru, то = (k2/Ru)IU = k2IU = k3P
Таким образом, по углу поворота подвижной части ваттметра можно судить о мощности цепи.
Шкала ваттметраравномерна. При работе с ваттметром необходимо иметь в виду, что изменение направления тока в одной из катушек вызывает изменение направления вращающего момента и направления поворота подвижной катушки, а так как обычно шкала ваттметра делаетсяодносторонней, т. е. деления шкалы расположены от нуля вправо, то при неправильном направлении тока в одной из катушек определение измеряемой величины по ваттметру будет невозможно.
По указанным причинам следует всегда различать зажимы ваттметра. Зажим последовательной обмотки, соединяемый с источником питания, называется генераторным и отмечается на приборах и схемах звездочкой. Зажим параллельной цепи, присоединяемый к проводу, соединенному с последовательной катушкой, также называется генераторным и отмечается звездочкой.
Таким образом, при правильной схеме включения ваттметра токи в катушках ваттметра направлены от генераторных зажимов к негенераторным. Могут иметь место две схемы включения ваттметра (см. рис. 2 и рис. 3).
Рис. 2. Правильная схема включения ваттметра
Рис. 3. Правильная схема включения ваттметра
В схеме, данной на рис. 2, ток последовательной обмотки ваттметра равен току приемников энергии, мощность которых измеряется, а параллельная цепь ваттметра находится под напряжением U‘ большим, чем напряжение приемников, на величину падения напряжения в последовательной катушке. Следовательно, Рв = IU’ = I(U+U1) = IU = IU1, т. е. мощность, измеряемая ваттметром, равна мощности приемников энергии, подлежащей измерению, и мощности последовательной обмотки ваттметра.
В схеме, данной на рис. 3, напряжение на параллельной цепи ваттметра равно напряжению на приемниках, а ток в последовательной обмотке больше тока, потребляемого приемником, на величину тока параллельной цепи ваттметра. Следовательно, Pв = U(I+Iu) = UI+ UIu, т. е. мощность, измеряемая ваттметром, равна мощности приемников энергии, подлежащей измерению, и мощности параллельной цепи ваттметра.
При измерениях, в которых мощностью обмоток ваттметра можно пренебречь, предпочтительнее пользоваться схемой, показанной на рис. 2, так как обычно мощность последовательной обмотки меньше, чем параллельной, а следовательно, показания ваттметра будут более точными.
При точных измерениях необходимо вводить поправки в показания ваттметра, обусловленные мощностью его обмотки, и в таких случаях можно рекомендовать схему на рис.3, так как поправка легко вычисляется по формуле U2/Ru, где Ru обычно известно, а поправка остается неизменной при различных значениях тока, если U постоянно.
10.12.2016 Без рубрики
§102. Измерение мощности и электрической энергии
Измерение мощности. В цепях постоянного тока мощность измеряют электро- или ферродинамическим ваттметром. Мощность может быть также подсчитана перемножением значений тока и напряжения, измеренных амперметром и вольтметром.
В цепях однофазного тока измерение мощности может быть осуществлено электродинамическим, ферродинамическим или индукционным ваттметром. Ваттметр 4 (рис. 336) имеет две катушки: токовую 2, которая включается в цепь последовательно, и напряжения 3, которая включается в цепь параллельно.
Ваттметр является прибором, требующим при включении соблюдения правильной полярности, поэтому его генераторные зажимы (зажимы, к которым присоединяют проводники, идущие со стороны источника 1) обозначают звездочками.
Рис. 336. Схема для измерения мощности
Для расширения пределов измерения ваттметров их токовые катушки включают в цепь при помощи шунтов или измерительных трансформаторов тока, а катушки напряжения — через добавочные резисторы или измерительные трансформаторы напряжения.
Измерение электрической энергии. Способ измерения. Для учета электрической энергии, получаемой потребителями или отдаваемой источниками тока, применяют счетчики электрической энергии. Счетчик электрической энергии по принципу своего действия аналогичен ваттметру. Однако в отличие от ваттметров вместо спиральной пружины, создающей противодействующий момент, в счетчиках предусматривают устройство, подобное электромагнитному демпферу, создающее тормозящее усилие, пропорциональное частоте вращения подвижной системы. Поэтому при включении прибора в электрическую цепь возникающий вращающий момент будет вызывать не отклонение подвижной системы на некоторый угол, а вращение ее с определенной частотой.
Число оборотов подвижной части прибора будет пропорционально произведению мощности электрического тока на время, в течение которого он действует, т. е. количеству электрической энергии, проходящей через прибор. Число оборотов счетчика фиксируется счетным механизмом. Передаточное число этого механизма выбирают так, чтобы по показаниям счетчика можно было отсчитывать не обороты, а непосредственно электрическую энергию в киловатт-часах.
Наибольшее распространение получили ферродинамические и индукционные счетчики; первые применяют в цепях постоянного тока, вторые — в цепях переменного тока. Счетчики электрической энергии включают в электрические цепи постоянного и переменного тока так же, как и ваттметры.
Ферродинамический счетчик (рис. 337) устанавливают на э. п. с. постоянного тока. Он имеет две катушки: неподвижную 4 и подвижную 6. Неподвижная токовая катушка 4 разделена на две части, которые охватывают ферромагнитный сердечник 5 (обычно из пермаллоя). Последний позволяет создать в приборе сильное магнитное поле и значительный вращающий момент, обеспечивающий нормальную работу счетчика в условиях тряски и вибраций. Применение пермаллоя способствует уменьшению погрешности счетного механизма 2 от гистерезиса магнитной системы (он имеет весьма узкую петлю гистерезиса).
Чтобы уменьшить влияние внешних магнитных полей на показания счетчика, магнитные потоки отдельных частей токовой катушки имеют взаимно противоположное направление (астатическая система). При этом внешнее поле, ослабляя поток одной части, соответственно усиливает поток другой части и оказывает в целом небольшое влияние на результирующий вращающий момент, создаваемый прибором. Подвижная катушка 6 счетчика (катушка напряжения) расположена на якоре, выполненном в виде диска из изоляционного материала или в виде алюминиевой чаши. Катушка состоит из отдельных секций, соединенных с пластинами коллектора 7 (эти соединения на рис. 337 не показаны), по которому скользят щетки из тонких серебряных пластин.
Ферродинамический счетчик работает принципиально как двигатель постоянного тока, обмотка якоря которого подключена параллельно, а обмотка возбуждения — последовательно с потребителем электроэнергии. Якорь вращается в воздушном зазоре между полюсами сердечника. Тормозной момент создается в результате взаимодействия потока постоянного магнита 1 с вихревыми токами, возникающими в алюминиевом диске 3 при его вращении.
Для компенсации влияния момента трения и уменьшения благодаря этому погрешности прибора в ферродинамических счетчиках устанавливают компенсационную катушку или в магнитном поле неподвижной (токовой) катушки помещают лепесток из пермаллоя, который имеет высокую магнитную проницаемость при малой напряженности поля. При небольших нагрузках этот лепесток усиливает магнитный поток токовой катушки, что приводит к увеличению вращающего момента и компенсации трения. При увеличении нагрузки индукция магнитного поля катушки увеличивается, лепесток насыщается и его компенсирующее действие перестает возрастать.
При работе счетчика на э. п. с. возможны сильные толчки и удары, при которых щетки могут отскакивать от коллекторных пластин. При этом под щетками будет возникать искрение. Для его предотвращения между щетками включают конденсатор С и резистор R1. Компенсация температурной погрешности осуществляется с помощью термистора Rт (полупроводникового прибора, сопротивление которого зависит от температуры). Он включается совместно с добавочным резистором R2 параллельно подвижной катушке. Чтобы уменьшить влияние тряски и вибраций на работу счетчиков, их устанавливают на э. п. с. на резинометаллических амортизаторах.
Индукционный счетчик имеет два электромагнита (рис. 338,а), между которыми расположен алюминиевый диск 7. Вращающий момент в приборе создается в результате взаимодействия переменных магнитных потоков Ф1 и Ф2, созданных катушками электромагнитов, с вихревыми токами Iв1 и Iв2, индуцируемыми ими в алюминиевом диске (так же, как и в обычном индукционном измерительном механизме, см. § 99).
В индукционном счетчике вращающий момент М должен быть пропорционален мощности P=UIcos?. Для этого катушку 6 одного из электромагнитов (токовую) включают последовательно с нагрузкой 5, а катушку 2 другого (катушку напряжения) — параллельно нагрузке. В этом случае магнитный поток Ф1 будет пропорционален току I в цепи нагрузки, а поток Ф2 — напряжению U, приложенному к нагрузке. Для обеспечения требуемого угла сдвига фаз ? между потоками Ф1 и Ф2 (чтобы sin? = cos?) в электромагните катушки напряжения предусмотрен магнитный шунт 3, через который часть потока Ф2 замыкается
Рис. 337. Ферродинамический счетчик электрической энергии
Рис. 338. Индукционный счетчик электрической энергии
помимо диска 7. Угол сдвига фаз между потоками Ф1 и Ф2 точно регулируется изменением положения металлического экрана 1, расположенного на пути потока, ответвляющегося через магнитный шунт 3.
Тормозной момент создается так же, как в ферродинамическом счетчике. Компенсация момента трения осуществляется путем создания небольшой несимметрии в магнитной цепи одного из электромагнитов с помощью стального винта.
Для предотвращения вращения якоря при отсутствии нагрузки под действием усилия, созданного устройством, компенсирующим трение, на оси счетчика укрепляется стальной тормозной крючок. Этот крючок притягивается к тормозному магниту 4, благодаря чему предотвращается возможность вращения подвижной системы без нагрузки.
При работе же счетчика под нагрузкой тормозной крючок практически не влияет на его показания.
Чтобы диск счетчика вращался в требуемом направлении, необходимо соблюдать определенный порядок подключения проводов к его зажимам. Нагрузочные зажимы прибора, к которым подключают провода, идущие от потребителя, обозначают буквами Я (рис. 338,б), генераторные зажимы, к которым подключают провода от источника тока или от сети переменного тока,— буквами Г.
Подключение ваттметра. Включение ваттметра в измеряемую цепь. Включение ваттметра в цепь переменного тока, при токе нагрузки больше допустимого
Сегодня нами будет рассмотрена катушка индуктивности в цепи переменного тока, узнаем, в чем бы была разница, если бы цепь питалась от постоянного тока, а также много интересных особенностей этого простого, но очень важного радиоэлемента.
Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.
Что такое катушка индуктивности
Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:
- Сглаживание биений;
- Подавление помех;
- Ограничение переменного тока;
- Накопление энергии и прочее.
Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.
- Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
- Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.
- Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.
Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.
- Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
- Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.
- Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.
Конструкционные особенности
Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.
Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.
Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.
Применение
Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.
Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.
Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.
Для справки! Трансформаторы способны функционировать только с переменным током.
Основные характеристики катушек индуктивности
Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.
- Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока. Измеряется этот параметр в Генри (Гн).
- Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
- Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.
Il = U / XL и IC = U / XC
Резонанс токов
Следовательно:
fрез = 1 / 2π√LC
Lрез = 1 / ω 2 С
Срез = 1 / ω 2 L
Резонанс напряжений
Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой последовательно, то резонанс в такой цепи называется последовательным резонансом или резонансом напряжений. Характерная черта резонанса напряжений — значительные напряжения на емкости и на индуктивности, по сравнению с ЭДС источника.
Причина появления такой картины очевидна. На активном сопротивлении по закону Ома будет напряжение Ur, на емкости Uc, на индуктивности Ul, и составив отношение Uc к Ur можно найти величину добротности Q. Напряжение на емкости будет в Q раз больше ЭДС источника, такое же напряжение окажется приложенным к индуктивности.
То есть резонанс напряжений приводит к возрастанию напряжения на реактивных элементах в Q раз, а резонансный ток будет ограничен ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, сопротивление последовательного контура на резонансной частоте минимально.
Резонанс токов
Когда источник ЭДС, емкость, индуктивность и сопротивление включены между собой параллельно, то резонанс в такой цепи называется параллельным резонансом или резонансом токов. Характерная черта резонанса токов — значительные токи через емкость и индуктивность, по сравнению с током источника.
Причина появления такой картины очевидна. Ток через активное сопротивление по закону Ома будет равен U/R, через емкость U/XC, через индуктивность U/XL, и составив отношение IL к I можно найти величину добротности Q. Ток через индуктивность будет в Q раз больше тока источника, такой же ток будет течь каждые пол периода в конденсатор и из него.
То есть резонанс токов приводит к возрастанию тока через реактивные элементы в Q раз, а резонансная ЭДС будет ограничена ЭДС источника, его внутренним сопротивлением и активным сопротивлением цепи R. Таким образом, на резонансной частоте сопротивление параллельного колебательного контура максимально.
Применение резонанса токов
Аналогично резонансу напряжений, резонанс токов применяется в различных фильтрах. Но включенный в цепь, параллельный контур действует наоборот, чем в случае с последовательным: установленный параллельно нагрузке, параллельный колебательный контур позволит току резонансной частоты контура пройти в нагрузку, поскольку сопротивление самого контура на собственной резонансной частоте максимально.
Установленный последовательно с нагрузкой, параллельный колебательный контур не пропустит сигнал резонансной частоты, поскольку все напряжение упадет на контуре, а на нагрузку придется мизерная доля сигнала резонансной частоты.
Так, основное применение резонанса токов в радиотехнике — создание большого сопротивления для тока определенной частоты в ламповых генераторах и усилителях высокой частоты.
В электротехнике резонанс токов используется с целью достижения высокого коэффициента мощности нагрузок, обладающих значительными индуктивными и емкостными составляющими.
Например, установки компенсации реактивной мощности (КРМ) представляют собой конденсаторы, подключаемые параллельно обмоткам асинхронных двигателей и трансформаторов, работающих под нагрузкой ниже номинальной.
К таким решениям прибегают как раз с целью достижения резонанса токов (параллельного резонанса), когда индуктивное сопротивление оборудования делается равным емкостному сопротивлению подключаемых конденсаторов на частоте сети, чтобы реактивная энергия циркулировала между конденсаторами и оборудованием, а не между оборудованием и сетью; чтобы сеть отдавала энергию только тогда, когда оборудование нагружено и потребляет активную мощность.
Когда же оборудование работает в холостую, сеть оказывается подключена параллельно резонансному контуру (внешние конденсаторы и индуктивность оборудования), который представляет для сети очень большое комплексное сопротивление и позволяет снизитьсякоэффициенту мощности.
ЛитератураПравить
§ Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 928.
§ Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.
Параллельное включение конденсатора и катушки индуктивности в цепь переменного тока
Рассмотрим явления в цепи переменного тока, содержащей генератор, конденсатор и катушку индуктивности, соединенные параллельно. Предположим при этом, что активным сопротивлением цепь не обладает.
Очевидно, в такой цепи напряжение как на катушке, так и на конденсаторе в любой момент времени равно напряжению, развиваемому генератором.
Общий же ток в цепи слагается из токов в ее разветвлениях. Ток в индуктивной ветви отстает по фазе от напряжения на четверть периода, а ток в емкостной ветви опережает его на те же четверть периода. Поэтому токи в ветвях в любой момент времени оказываются сдвинутыми по фазе один относительно другого на полупериода, т. е. находятся в противофазе. Таким образом токи в ветвях в любой момент времени направлены навстречу один другому, а общий ток в неразветвленной части цепи равен разности их.
Это дает нам право написать равенство I = IL -IC
где I — действующее значение общего тока в цепи, IL и IC — действующие значения токов в.ветвях.
Пользуясь законом Ома для определения действующих значений тока в ветвях, получим:
Il = U / XL и IC = U / XC
Если в цепи преобладает индуктивное сопротивление, т. е. XL больше XC, ток в катушке меньше тока в конденсаторе; следовательно, ток в неразветвленном участке цепи носит емкостный характер, и цепь в целом для генератора будет емкостной. И, наоборот, при ХC большем XL, ток в конденсаторе меньше тока в катушке; следовательно, ток в неразветвленном участке цепи имеет индуктивный характер, и цепь в целом для генератора будет индуктивной.
При этом не следует забывать, что в том и другом случае нагрузка реактивная, т. е. цепь не потребляет энергии генератора.
Резонанс токов
Рассмотрим теперь случай, когда у параллельно соединенных конденсатора и катушки оказались равными их реактивные сопротивления, т. е. XlL = XC.
Если мы, как и прежде, будем считать, что катушка и конденсатор не обладают активным сопротивлением, то при равенстве их реактивных сопротивлений (YL = YC) общий ток в неразветвленной части цепи окажется равным нулю, тогда как в ветвях будут протекать равные токи наибольшей величины. В цепи в этом случае наступает явление резонанса токов.
При резонансе токов действующие значения токов в каждом разветвлении, определяемые отношениями IL = U / XL и IC= U / XC будут равны между собой, так XL = ХC.
Вывод, к которому мы пришли, может показаться на первый взгляд довольно странным. Действительно, генератор нагружен двумя сопротивлениями, а тока в неразветвленной части цепи нет, тогда как в самих сопротивлениях протекают равные и притом наибольшие по величине токи.
Объясняется это поведением магнитного поля катушки и электрического поля конденсатора. При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, сказывается как бы изолированным. Его можно было бы совсем отключить, и ток в разветвленной части цепи поддерживался бы без генератора энергией, которую в самом начале запасла цепь. Равно и напряжение на зажимах цепи оставалось бы точно таким, какое развивал генератор.
Таким образом, и при параллельном соединении катушки индуктивности и конденсатора мы получили колебательный контур, отличающийся от описанного выше только тем, что генератор, создающий колебания, не включен непосредственно в контур и контур получается замкнутым.
Графики токов, напряжения и мощности в цепи при резонансе токов: а — активное сопротивление равно нулю, цепь мощности не потребляет; б — цепь обладает активным сопротивлением, в неразветвленной части цепи появился ток, цепь потребляет мощность
Значения L, С и f, при которых наступает резонанс токов, определяются, как и при резонансе напряжений (если пренебречь активным сопротивлением контура), из равенства:
Следовательно:
fрез = 1 / 2π√LC
Lрез = 1 / ω 2 С
Срез = 1 / ω 2 L
Изменяя любую из этих трех величин, можно добиться равенства Xl = Xc, т. е. превратить цепь в колебательный контур.
Итак, мы получили замкнутый колебательный контур, в котором можно вызвать электрические колебания, т. е. переменный ток. И если бы не активное сопротивление, которым обладает всякий колебательный контур, в нем непрерывно мог бы существовать переменный ток. Наличие же активного сопротивления приводит к тому, что колебания в контуре постепенно затухают и, чтобы поддержать их, необходим источник энергии — генератор переменного тока.
В цепях несинусоидального тока резонансные режимы возможны для различных гармоничных состовляющих.
Резонанс токов широко используется в практике. Явление резонанса токов используется в полосовых фильтрах как электрическая «пробка», задерживающая определенную частоту. Так как току с частотой f оказывается значительное сопротивление, то и падение напряжения на контуре при частоте f будет максимальным. Это свойство контура получило название избирательность, оно используется в радиоприемниках для выделения сигнала конкретной радиостанции. Колебательный контур, работающий в режиме резонанса токов, является одним из основных узловэлектронных генераторов.
Если в цепь переменного тока включены последовательно катушка индуктивности иконденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением.
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки X L и емкостного сопротивления конденсатора Х С.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
Применив к этой цепи закон Ома, получим:
Формулу эту можно преобразовать следующим образом:
В полученном равенстве IX L -действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а IХ С -действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
где R — общее активное сопротивление цепи, X L -Х С — ее общее реактивное сопротивление. Переходя к формуле закона Ома, мы вправе написать:
Переменный ток
Как известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток.
Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток.
Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника
Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:
u=Um⋅sinωt u=Um⋅sinωt или u=Um⋅cosωt u=Um⋅cosωt ,
где u – мгновенное значение напряжения, U m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω , то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
i=Im⋅sin(ωt+φc) i=Im⋅sin(ωt+φc) ,
где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Резистор в цепи переменного тока
Пусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R , которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением . В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление R называется активным потому, что, только на нем выделяется энергия, т.е.
Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением .
Итак, в цепи имеется резистор, активное сопротивление которого R , а катушка индуктивности и конденсатор отсутствуют (рис. 1).
Пусть напряжение на концах цепи меняется по гармоническому закону
u=Um⋅sinωt u=Um⋅sinωt .
Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:
i=UR=Um⋅sinωtR=Im⋅sinωt i=UR=Um⋅sinωtR=Im⋅sinωt .
Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление:
При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока.
Применение: Постоянный ток широко используется в технике: подавляющее большинство электронных схем в качестве питания используют постоянный ток. Переменный ток используется преимущественно для более удобной передачи от генератора до потребителя. Иногда в некоторых устройствах постоянный ток преобразуют в переменный ток преобразователями (инверторами).
ЗАКОНЫ ПОСТОЯННОГО ТОКА
Всякое движение электрических зарядов называют электрическим током. В металлах могут свободно перемещаться электроны, в проводящих растворах — ионы, в газах могут существовать в подвижном состоянии и электроны, и ионы.
Условно за направление тока считают направление движения положительных частиц, поэтому металлахнаправление тивоположно направлению движения электронов.
Плотность тока — величина заряда, проходящего в единицу времени через единицу поверхности, перпендикулярной к линиям тока. Эта величина обозначается j и рассчитывается следующим образом:
Здесь n — концентация заряженных частиц, e — заряд каждой из частиц, v — их скорость.
Сила тока i — величина заряда, проходящего в единицу времени через полное сечение проводника. Если за время dt через полное сечение проводника прошел заряд dq, то
По другому, сила тока находится интегрированием плотности тока по всей поверхности любого сечения проводника. Единица измерения силы тока — Ампер. Если состояние проводника (его температура и др.) стабильно, то между приложенным к его концам напряжением и возникающим при этом током существует однозначная связь. Она называется Закон Ома и записывается так:
R — электрическое сопротивление проводника, зависящее от рода вещества и от его геометрических размеров. Единичным сопротивлением обладает проводник, в котором возникает ток 1 А при напряжении 1 В. Эта единица сопротивления называется Ом.
Закон Ома в дифференциальной форме:
где j — плотность тока, Е — напряженность поля, — проводимость. В этой записи закон Ома содержит величины, характеризующие состояние поля в одной и той же точке.
Различают последовательное и параллельное соединения проводников.
При последовательном соединении ток, протекающий по всем участкам цепи, одинаков, а напряжение на концах цепи складывается как алгебраическая сумма напряжений на всех участках
При параллельном соединении проводников постоянным остается напряжение, а ток складывается из суммы токов, протекающих по всем ветвям. В этом случае складываются величины, обратные сопротивлению:
Для получения постоянного тока на заряды в электрической цепи должны действовать силы, отличные от сил электростатического поля; их называют сторонними силами.
Если рассматривать полную электрическую цепь, необходимо включить в нее действие этих сторонних сил и внутренне сопротивление источника тока r. В этом случае закон Ома для полной цепи примет вид
Е — электродвижущая сила (ЭДС) источника. Она измеряется в тех же единицах, что и напряжение. Величину (R+r) называют иногда полным сопротивлением цепи.
Сформулируем правила Киркгофа :
Первое правило: алгебраическая сумма сил токов в участках цепи, сходящихся в одной точке разветвления, равна нулю.
Второе правило: для любого замкнутого контура сумма всех падений напряжения равна сумме всех ЭДС в этом контуре.
Мощность тока рассчитывается по формуле
Закон Джоуля-Ленца. Работа электрического тока (тепловое действие тока)
A=Q=UIt=I2Rt=U2t/R.
Электрический ток в металлах есть движение электронов, ионы металла участия в переносе электрического заряда не принимают. Другими словами, в металлах есть электроны, способные перемещаться по металлу. Они получили название электронов проводимости. Положительные заряды в металле представляют собой ионы, образующие кристаллическую решетку. В отсутствии внешнего поля электроны в металле движутся хаотично, претерпевая соударения с ионами решетки. Под воздействием внешнего электрического поля электроны начинают упорядоченное движение, накладывающееся на их прежние хаотические флуктуации. В процессе упорядоченного движения электроны по-прежнему сталкиваются с ионами кристаллической решетки. Именно этим и обусловлено электрическое сопротивление.
В классической электронной теории металлов предполагается, что движение электронов подчиняется законам классической механики. Взаимодействием электронов между собой пренебрегают, взаимодействие электронов с ионами сводят только к соударениям. Можно сказать, что электроны проводимости рассматривают как электронный газ, подобный идеальному атомарному газу в молекулярной физике. Поскольку средняя кинетическая энергия на одну степень свободы для такого газа равна kT/2, а свободный электрон обладает тремя степенями свободы, то
где v2t — среднее значение квадрата скорости теплового движения.
На каждый электрон действует сила, равная еЕ, в результате чего он приобретает ускорение еЕ/m. Скорость к концу свободного пробега равна
где t — среднее время между соударениями.
Поскольку электрон движется равноускоренно, его средняя скорость равна половине максимальной:
Среднее время между соударениями есть отношение длины свободного пробега к средней скорости:
Поскольку обычно скорость упорядоченного движения много меньше тепловой скорости, то скоростью упорядоченного движения пренебрегли.
Окончательно, имеем
Коэффициент пропорциональности между vc и Е называется подвижность электронов.
С помощью классической электронной теории газов могут быть объяснены многие закономерности — закон Ома, закон Джоуля-Ленца и другие явления, однако эта теория не может объяснить, например, явления сверхпроводимости:
При определенной температуре удельное сопротивление для некоторых веществ скачком уменьшается практически до нуля. Это сопротивление настолько мало, что однажды возбужденный в сверхпроводнике электрический ток существует длительное время без источника тока. Несмотря на скачкообразное изменение сопротивления, другие характеристики сверхпроводника (теплопроводность, теплоемкость и др.) не меняются либо меняются мало.
Более точным методом, объясняющим такие явления в металлах, является подход с использованием квантовой статистики.
Электрический ток в газах
В обычном состоянии газы не проводят электричества. Однако под влиянием различных внешних факторов (высокая температура, различные излучения) газы становятся электропроводящими. Это происходит вследствие того, что от нейтральных атомов отделяются электроны и образуются проводящие частицы — положительные ионы и свободные электроны. Часть свободных электронов может быть захвачена нейтральными атомами и образуются отрицательные ионы. Этот процесс называется ионизацией. Ионизация атома (отрыв электрона) требует определенной энергии, величина которой зависит от строения атома и называется энергией ионизации.
Если ионизацию не поддерживать, например, бомбардируя атомы электронами, ускоренными во внешнем электрическом поле, то со временем происходит рекомбинация ионов — положительный и отрицательный ион в результате теплового движения сталкиваются и избыточный электрон переходит к положительному иону. В результате образуется два нейтральных атома. Рассмотрим принципиальную схему, изображенную на рисунке:
Пусть на отрицательный электрод падают ультрафиолетовые лучи, обеспечивающие ионизацию газа. Если увеличивать напряжение между электродами (например, плавно уменьшая сопротивление r) то сила тока будет увеличиваться, пока не достигнет максимума (тока насыщения), при котором все свободные электроны достигают противоположного электрода.
Сила тока насыщения зависит только от интенсивности процесса ионизации (в нашем случае, от интенсивности ультрафиолетовых лучей). Если снять внешнюю ионизацию, разряд между электродами исчезнет. Такие разряды называются несамостоятельными. Если же продолжать уменьшать сопротивление (увеличивая тем самым напряжение) произойдет резкое (в сотни раз) увеличение силы тока, в газе появятся световые и тепловые эффекты. Если прекратить действие ионизатора, то разряд будет продолжаться. Это значит, что новые ионы для поддержания разряда образуются благодаря процессам в самом разряде. Такие разряды называют самостоятельными.
Дело в том, что с увеличением напряжения возрастает скорость и кинетическая энергия электрона, и он при столкновении с атомом сам способен произвести его ионизацию — высвободить еще один электрон. На следующем этапе два электрона образуют уже четыре и т.д. Происходит лавинообразное увеличение количества носителей. Это явление получило название электронной (или ионной) лавины, а напряжение, при котором это происходит — напряжением пробоя газового промежутка (напряжением зажигания газового разряда).
В зависимости от свойств и внешнего вида разрядов различают коронный, искровой, дуговой, тлеющий и другие разряды.
В различных формах газового разряда иногда образуется сильно ионизированный газ, в котором концентрация электронов приблизительно равна концентрации положительных ионов. Такая система получила название ионной плазмы.
Ток в вакууме
Как известно, в металлах имеются электроны проводимости, образующие «электронный газ» и участвующие в тепловом движении. Для того, чтобы свободный электрон мог выйти из металла, должна быть совершена определенная работа, различная для разных металлов и названная работой выхода.
Существование работы выхода показывает, что в поверхностном слое металла существует электрическое поле, значит, электрический потенциал при переходе через этот слой изменяется на некоторую величину, также специфичную для разных металлов. Эта поверхностная разность потенциалов связана с работой выхода соотношением:
Поскольку выйти из металла могут только «самые быстрые» электроны, то можно записать условие выхода так mv 2 /2>ef
В обычных условиях работа выхода в сотни раз больше энергии теплового движения электронов, поэтому подавляющее большинство их остается в металле. Но если сообщить электронам дополнительную энергию, можно наблюдать явление испускания электронов или электронной эмиссии. В зависимости от того, каким образом сообщена дополнительная энергия, различают термоэлектронную эмиссию, фотоэмиссию, вторичную электронную эмиссию и др.
Для наблюдения термоэлектронной эмиссии используется принципиальная схема, содержащая вакуумный диод (см. рис.).
В такой цепи возникнет ток, только если катод раскалить до высокой температуры. Вольт-амперная характеристика диода показывает, что при нулевой разности потенциалов ток очень мал. В дальнейшем, при увеличении потенциала на аноде, увеличивается и ток, пока не достигнет некоторого постоянного значения — тока насыщения Is. Его значение увеличивается с увеличением температуры катода. Также с увеличением температуры растет и напряжение Us, при котором достигается ток насыщения.
По графику наглядно видно, что зависимость между током и напряжением для диода носит нелинейный характер, то есть диод не подчиняется закону Ома. Богуславский и Лэнгмюр независимо друг от друга показали, что зависимость тока диода от потенциала анода имеет вид:
Где С зависит от формы и размеров электродов.
Зависимость плотности тока насыщения от температуры известна под названием формулы Ричардсона:Js=CT 1/2 exp(-ef/kT),
где С — константа, различная для разных металлов. Эта формула выведена на основании классической электронной теории. Квантовая теория металлов дает следующее соотношение:Js=АT 2 exp(-ef/kT)
Заметим, что это различие не существенно, так как зависимость плотности тока от температуры определяется главным образом экспоненциальным множителем exp(-e/kT).
Соединение в звезду
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной.
Все величины, относящиеся к фазам, носят название фазных переменных, к линии — линейных. Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе
.
Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; — фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
; (1)
; (2)
. (3)
Отметим, что всегда — как сумма напряжений по замкнутому контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае
Обычно при расчетах принимается . Тогда для случая прямого чередования фаз , (при обратном чередовании фаз фазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем:
;
.
3. Соединение источника энергии и приемника по схеме треугольник .В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
.
Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
Аналогично можно выразить линейные токи через фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
Помимо рассмотренных соединений «звезда — звезда» и «треугольник — треугольник» на практике также применяются схемы «звезда — треугольник» и «треугольник — звезда».
Явление резонанса
Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.
Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.
Для определения условий возникновения режима резонанса в электрической цепи нужно:
найти ее комплексное сопротивление или проводимость;
выделить мнимую часть и приравнять нулю.
Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.
Уравнение Im[Z]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.
В электрических цепях резонанс может рассматриваться в задачах:
анализа этого явления при вариации параметров цепи;
синтеза цепи с заданными резонансными параметрами.
Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.
Сдвиг фаз между током и напряжением. Понятие двухполюсника
Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром . Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резистивным сопротивлением следует учитывать по крайней мере сопротивления проводников.
Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно
Условием резонанса из выражения (1) будет
Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления R когда индуктивное сопротивление xL = wL равно емкостному xC = 1/(wC) . Как следует из выражения (2), это состояние может быть получено вариацией любого их трех параметров — L, C и w , а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде
Все величины, входящие в выражение (3) положительны, поэтому эти условия выполнимы всегда, т.е. резонанс в последовательном контуре можно создать
изменением индуктивности L при постоянных значениях C и w ;
изменением емкости C при постоянных значениях L и w ;
изменением частоты w при постоянных значениях L и C.
Наибольший интерес для практики представляет вариация частоты. Поэтому рассмотрим процессы в контуре при этом условии.
При изменении частоты резистивная составляющая комплексного сопротивления цепи Z остается постоянной, а реактивная изменяется. Поэтому конец вектора Z на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку R вещественной оси (рис. 1 б)). В режиме резонанса мнимая составляющая Z равна нулю и Z = Z = Zmin = R , j = 0 , т.е. полное сопротивление при резонансе соответствует минимальному значению .
Индуктивное и емкостное сопротивления изменяются в зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к нулю xC®µ , xL® 0 , и j® — 90° (рис. 1 б)). При бесконечном увеличении частоты — xL®µ , xC ® 0 , а j® 90° . Равенство сопротивлений xLи xC наступает в режиме резонанса при частоте w0 .
Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, обладающего свойствами источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в контуре равен i=Imsinwt. Падение напряжения на входе уравновешивается суммой напряжений на элементах
Переходя от амплитудных значений к действующим, из выражения (4) получим напряжения на отдельных элементах контура
а при резонансной частоте
величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура.
Следовательно, при резонансе
напряжение на резисторе равно напряжению на входе контура;
напряжения на реактивных элементах одинаковы и пропорциональны волновому сопротивлению контура;
соотношение напряжения на входе контура (на резисторе) и напряжений на реактивных элементах определяется соотношением резистивного и волнового сопротивлений.
Отношение волнового сопротивления к резистивному r /R = Q, называется добротностью контура , а величина обратная D=1/Q — затуханием . Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений .
Рассмотрим зависимости напряжений и тока в контуре от частоты. Для возможности обобщенного анализа перейдем в выражениях (5) к относительным единицам, разделив их на входное напряжение при резонансе
где i =I/I0, uk=Uk/U, v = w /w0 — соответственно ток, напряжение и частота в относительных единицах, в которых в качестве базовых величин приняты ток I0, напряжение на входе U и частота w0 в режиме резонанса.
Абсолютный и относительный ток в контуре равен
Из выражений (7) и (8) следует, что характер изменения всех величин при изменении частоты зависит только от добротности контура. Графическое представление их при Q=2 приведено на рис. 3 в логарифмическом (а) и линейном (б) масштабах оси абсцисс.
На рис. 3 кривые A(v), B(v) и C(v) соответствуют напряжению на индуктивности, емкости и резисторе или току в контуре. Кривые A(v)=uL(v) и B(v)=uC(v) имеют максимумы, напряжения в которых определяются выражением
, (9)
а относительные частоты максимумов равны
(10)
При увеличении добротности Q ®µAmax = Bmax®Q,
С уменьшением добротности максимумы кривых uL(v) и uС(v) смещаются от резонансной частоты, а при Q2
Напряжение на резисторе и ток в контуре имеют при резонансной частоте максимум равный 1,0. Если на оси ординат отложить абсолютные значения тока или напряжения на резисторе, то для различных значений добротности они будут иметь вид, показанный на рис. 4. В целом они дают представлние о характере изменения величин, но удобнее делать сопоставление в относительных единицах.
На рис. 5 представлены кривые рис. 4 в относительных единицах. Здесь видно, что увеличение добротности влияет на скорость изменения тока при изменении частоты.
Можно показать, что разность относительных частот, соответствующих значениям относительного тока , равна затуханию контура D=1/Q =v2-v1.
Перейдем теперь к анализу зависимости фазового сдвига между током и напряжением на входе контура от частоты. Из выражения (1) угоj j равен
Как и следовало ожидать, значение j определяется добротностью контура. Графически эта зависимость для двух значений добротности показана на рис. 6 .
При уменьшении частоты значение фазового сдвига стремится к значению — 90° , а при увеличении к +90° , проходя через нулевое значение при частоте резонанса. Скорость изменения функции j (v) определяется добротностью контура.
Последовательный резонансный контур может питаться также от источника электрической энергии, обладающего свойствами источника тока, т.е. обеспечивающего постоянный ток в нагрузке. Выражения (5) остаются справедливыми и в этом случае, но ток в них будет константой. Поэтому постоянным будет падение напряжения на резисторе UR = RI = const. Разделив все напряжения на это базовое значение, В выражении (12) добротность также есть отношение волнового сопротивления к резистивному Q=r /R .
Общее относительное падение напряжения на входе контура является гипотенузой прямоугольного еугольника напряжений, поэтому
Функции uL(v) и uС(v) монотонны, а u(v) имеет минимум u =1.0 при резонансной частоте, когда uL(v) -uС(v) = 0. В случае стремления относительной частоты к бесконечности и к нулю, напряжения на одном из реактивных элементов стремится к бесконечности. При резонансной частоте они одинаковы и их отношение ко входному напряжению равно добротности.
Графическое представление функций uL(v)=A(v), uС(v)=B(v) и u(v)=С(v) при добротности Q=2 дано на рис. 7 в логарифмическом (а) и линейном (б) масштабах оси частот.
Для функции u (v)=С(v) можно показать, что разность относительных частот v1 и v2 , соответствующих значениям , равна затуханию контура D=1/Q=v2-v1.
Фазовые характеристики контура при питании от источника тока ничем не отличаются от характеристик режима питания от источника ЭДС (рис. 6).
Сопоставляя частотные характеристики при питании последовательного резонансного контура от источника тока с характеристиками при питании его от источника ЭДС, можно сделать следующие выводы:
частотные характеристики напряжений и тока контура принципиально отличаются друг от друга, т.к. при питании от источника ЭДС сумма напряжений остается постоянной и происходит только их перераспределение между элементами, а при питании от источника тока падения напряжения на каждом элементе формируются независимо;
режимы резонанса для обоих случаев полностью идентичны;
фазовые частотные характеристики для обоих случаев также идентичны.
Режим резонанса можно создать также при параллельном соединении R, L и C (рис. 8а)). Такая цепь называется параллельным резонансным контуром . В этом случае условие резонанса удобнее сформулировать для мнимой части комплексной проводимости в виде
Следовательно, для параллельного контура возможны те же вариации параметров, что и для последовательного и выражения для них будут идентичным
900+
При изменении частоты питания изменяется только мнимая составляющая вектора комплексной проводимости Y , поэтому его конец перемещается на комплексной плоскости по прямой параллельной мнимой оси и проходящей через точку G=1/R , соответствующую вещественной составляющей проводимости (рис. 8 б)). При частоте резонанса модуль вектора минимален, а при стремлении частоты к нулю и бесконечности, его значение стремится к бесконечности. При этом угол сдвига фаз между током и напряжением j на входе контура стремится к 90° при w® 0 и к — 90° при w®µ .
Для параллельного соединения токи в отдельных элементах можно представить через проводимости и общее падение напряжения U в витщ
Пусть в режиме резонанса падение напряжения на входе контура равно U0, тогда токи в отдельных элементах будут
волновая или характеристическая проводимость контура. Как следует из выражений (17), при резонансе токи в реактивных элементах одинаковы, а входной ток равен току в резисторе R. Отношение Q=g /G называется добротностью, а величина обратная D=1/Q — затуханием параллельного резонансного контура. Таким образом, добротность равна отношению токов в реактивных элементах контура к току на входе или в резисторе. В электрических цепях добротность может достигать значений в несколько десятков единиц и во столько же раз токи в индуктивности и емкости будут превышать входной ток. Поэтому резонанс в параллельном контуре называется резонансом токов .
Падение напряжения на входе контура U при питании его от источника, обладающего свойствами источника тока и формирующего ток с действующим значением I, будет равно
Для включения ваттметра его генераторные зажимы (зажимы, обозначенные *I и *V), соединяются накоротко одним проводником. Для правильного показания ваттметра оба генераторных зажима должны быть присоединены к одному проводу со стороны генератора источника тока, а не нагрузки. Затем другим проводом включается последовательно в цепь неподвижная катушка; при этом в зависимости от предела тока этот провод подключается к зажиму 1А – при измеряемом токе не превышающем 1А, или 5А при токе, не превышающем 5А.
Затем включается параллельно цепи рамки; для этого предварительно к зажиму подключается одно из дополнительных сопротивлений (в зависимости от предела напряжения: 30V – до 30В, 150V – до 150В и 300V – 300В).
В передний паз крышки прибора устанавливается рабочая шкала так, чтобы лицевая сторона прибора была обращена к шкале с пределом измерения, равным произведению предела по току на предел по напряжению.
Опыты с ваттметром
Ниже описаны только отдельные опыты, характеризующие возможности демонстрационного ваттметра.
Опыт 1. Измерение мощности в цепи однофазного переменного тока с активной нагрузкой.
Для выполнения этого опыта собирают электрическую цепь по схеме, приведённой на рисунке 3.
При проведении опыта целесообразно иметь возможность плавного изменения напряжения, поэтому следует провода А, Б подключить к зажимам регулируемого напряжения школьного распределительного щита или воспользоваться школьным регулятором напряжения (или иным трансформатором), допускающим плавное или ступенчатое регулирование напряжения.
Рис. 6 Схема электрической цепи в опыте 1.
В качестве нагрузки следует включить ползунковый реостат сопротивлением до 20 Ом (с допустимым током 5А).
Ваттметр включают в цепь через добавочное сопротивление 150V и через зажим 5А (см. схему).
Остановив ползунок реостата так, что в цепь включается все сопротивления реостата, устанавливается напряжение на нагрузку 50В, и наблюдают показания ваттметра, вольтметра и амперметра. Затем повышают напряжение на нагрузку, устанавливая последовательно 60, 80, 100В наблюдая каждый раз показания всех приборов.
Результаты этого опыта подтверждают, что мощность равна произведению напряжения на силу тока.
Опыт 2. Измерение мощности в цепи трёхфазного тока с активной симметричной нагрузкой.
С помощью одного демонстрационного ваттметра можно произвести опыт по измерению активной мощности трёхфазного тока при равномерной нагрузке всех фаз (т.е. когда в каждую фазу включены одинаковые нагрузки).
Для проведения этого опыта собирают электрическую цепь, как показано на рисунке 7.
В каждую фазу в качестве нагрузки включают по одной электрической лампе одинакового сопротивления.
Измерительные приборы используются те же, что и в предыдущем опыте.
Пределы ваттметра (по току и напряжению) устанавливаются в зависимости от напряжения и мощности электрических ламп.
Р
ис.
7 Схема электрической цепи в опыте 2.
По показаниям приборов устанавливают, что мощность одной фазы равна произведению фазного напряжения на ток в фазе.
Учитывая полную симметрию цепи трёхфазного тока, приведённой на рисунке 4, высчитывают мощность всей цепи, умножив показания ваттметра на 3.
Основы > Задачи и ответы
Однофазные цепи переменного тока (страница 2)
12.
Конденсатор емкостью С = 8,36 мкФ включен на синусоидальное напряжение U=380 В частотой
f
=50 Гц.
Определить ток в цепи конденсатора.
Решение:
Емкостное сопротивление
Ток в цепи конденсатора при синусоидальном напряжении 380 В
Для получения ббльших токов требуются при данной частоте большие значения емкости.
13.
При включении конденсатора на синусоидальное напряжение U=220 В частотой
f
=50 Гц в цепи установился ток
I
=0,5 А.
Какую емкость имеет конденсатор?
Решение:
Из формулы емкостного сопротивления емкость
Метод определения емкости конденсатора, рассмотренный в данной задаче, является наименее точным, но он прост и не требует больших затрат для применения на практике.
14.
При включении разомкнутого на конце кабеля на напряжение U=6600 В частотой
f
=50 Гц в цепи установился ток I=2 А.
Пренебрегая электрическим сопротивлением кабеля, определить приближенно емкость кабеля на 1 км его длины, если длина кабеля 10 км.
Решение:
Изолированные друг от друга жилы кабеля представляют собой конденсатор. Если пренебречь сопротивлением жил кабеля, то ток холостой работы кабеля, т. е. ток в кабеле, разомкнутом на конце, можно считать чисто емкостным. В этом случае действительно соотношение
где
— емкостная проводимость.
Отсюда
При частоте f =50 Гц угловая частота , следовательно,
Емкость кабеля на 1 км его длины
Описанный способ определения емкости кабеля на 1 км его длины является очень приближенным (в нем пренебрегают активным сопротивлением жил кабеля и активной проводимостью утечки от жилы к жиле вследствие несовершенства изоляции; допускается равномерное распределение емкости по длине кабеля).
15. Какая емкость батареи конденсаторов требуется для получения реактивной (емкостной) мощности 152 ВАР при напряжении U=127 В и частоте f= 50 Гц.
Решение:
При частоте
f=
50 Гц угловая частота
. Так как ток батареи считается чисто
реактивным (опережающим по фазе напряжение на 1
/
4 периода), то реактивная мощность равна произведению напряжения и тока:
Емкостный ток равен произведению напряжения на емкостную проводимость, поэтому
Емкость батареи конденсаторов
Реактивную (емкостную) мощность можно представить в виде , выразив ток через напряжение и емкостную проводимость; отсюда следует, что при данном напряжении и частоте реактивная (емкостная) мощность пропорциональна емкости. Если изоляция пластин батареи конденсаторов допускает повышение напряжения (например, в раз), то реактивная (емкостная) мощность увеличится пропорционально квадрату напряжения (т. е. в 3 раза). Таким образом, в рассматриваемом случае важное значение имеет отнонение напряжения от номинального.
16.
В катушке (см. задачу 10), включенной на переменное напряжение U=12 В частотой f=50 Гц установился ток 1,2 А.
Определить индуктивность катушки.
Решение:
Отношение переменного напряжения, приложенного к катушке, к току, устанавливающемуся в ней, называется
полным сопротивлением
z катушки;
В задаче 10 было определено, что активное сопротивление катушки r =2,8 Ом. Сопротивление катушки при перееденном токе больше сопротивления г при постоянном токе вследствие наличия э. д. с. самоиндукции, препятствующей изменению переменного тока. Это равносильно появлению в катушке сопротивления, называемого индуктивным:
где L — индуктивность, Гн
f — частота, Гц.
Связь между полным сопротивлением
z
, индуктивным сопротивлением
и активным сопротивлением
r
такая же, как между гипотенузой и катетами в прямоугольном треугольнике:
откуда индуктивное сопротивление
Индуктивность катушки
В рассматриваемой катушке ток отстает по фазе от напряжения, причем тангенс угла сдвига фаз .
17.
В схеме (рис. 23) вольтметр показывает 123 В, амперметр 3 А и ваттметр 81 Вт, частота сети 50 Гц.
Oпределить параметры катушки.
Решение:
Отношение напряжения к току равно полному сопротивлению катушки:
Ваттметр измеряет активную мощность цепи, которая в данной задаче является потерей мощноста в сопротивлении r , поэтому сопротивление катушки
Полное сопротивление
z
, активное сопротивление
r
и индуктивное сопротивление
катушки связаны между собой таким же соотношением, как гипотенуза и катеты в прямоугольном треугольнике.
Следовательно,
При частоте f =50 Гц угловая частота
Индуктивное сопротивление равно произведению угловой частоты w и индуктивности L; следовательно,
Коэффициент мощности катушки
. .
18.
Катушка без стального сердечника включена на постоянное напряжение 2,1 В, ток которой равен 0,3 А. При включении этой же катушки на синусоидальное напряжение частотой 50 Гц с действующим значением 50 В ток имеет действующее значение 2 А.
Определить параметры катушки, активную и полную мощности.
Решение:
Отношение постоянного напряжения к постоянному току в катушке практически равно (если пренебречь увеличением сопротивления из-за вытеснения переменного тока на поверхность провода) активному сопротивлению:
Это один из параметров катушки. Отношение этих же величин при переменном токе в катушке равно полному сопротивлению:
Индуктивное сопротивление:
Индуктивность катушки — второй ее параметр:
Коэффициент мощности катушки:
Из таблиц тригонометрических величин
.
Активная мощность
Полная мощность
Коэффициент мощности
В задачах 17 и 18 рассмотрены два различных способа определения параметров катушки.
19.
Батарея конденсаторов емкостью С=50 мкФ соединена последовательно с реостатом сопротивлением
r=
29,1 Ом.
Определить напряжения на батарее конденсаторов и реостате, а также ток в цепи и мощность, если приложенное напряжение U=210 В и частота сети
f
=50 Гц.
Решение:
Частоте 50 Гц и емкости 50 мкФ соответствует емкостное сопротивление, в 50 раз меньшее, чем емкости в 1 мкФ. Следовательно,
Здесь 3185 Ом — сопротивление конденсатора емкостью 1 мкФ.
По условию, сопротивление реостата
r
=29,1 Ом. Полное сопротивление цепи связано с активным и емкостным сопротивлениями таким же соотношением, как гипотенуза и катет прямоугольного треугольника:
Напряжение на реостате
Напряжение на батарее конденсаторов
В силу последовательного соединения большее напряжение оказалось на элементе цепи, имеющем большее сопротивление.
Коэффициент мощности
Из таблиц тригонометрических величин угол сдвига фаз
.
Активная мощность цепи
Полная мощность цепи равна произведению действующих значений напряжения и тока:
Полная мощность намного больше активной мощности, так как коэффициент мощности мал, т. е. полное сопротивление цепи во много раз превышает активное сопротивление.
20.
Электрическую лампу мощностью Р=60 Вт при напряжении
необходимо подсоединить к сети с переменным напряжением U=220 В и частотой 50 Гц. Для компенсации части этого напряжения последовательно с лампой включается конденсатор.
Какой емкости необходимо взять конденсатор?
Решение:
Напряжение на лампе будет активной составляющей приложенного напряжения сети, а напряжение на конденсаторе — его реактивной (емкостной) составляющей. Эти напряжения связаны соотношением
Напряжение на конденсаторе
Ток в конденсаторе тот же, что и в лампе, т. е.
На основании закона Ома емкостное сопротивление
Так как при частоте f=50 Гц емкости С=1 мкФ соответствует емкостное сопротивление
, то емкость рассматриваемого конденсатора приблизительно равна 8,7 мкФ.
Избыточное напряжение можно было бы скомпенсировать и путем последовательного включения реостата с лампой. Так как реостат, как и электрическая лампа, представляет чисто активное сопротивление, то напряжения на этих элементах цепи совпадают по фазе с общим током, а следовательно, и между собой. В этом случае будет действительно соотношение
где — напряжение на реостате, равное
При токе лампы 0,5 А сопротивление реостата должно составлять
В реостате будет расходоваться энергия, переходящая в тепло, причем потери мощности в реостате
В случае включения емкости «погашение» напряжения происходит без потерь энергии.
21.
В случае электрической сварки дугой тонких листов при переменном токе в ней развивается мощность
при токе
I
=20
A
. Напряжение источника
U
=120 В, частота сети
f
=50 Гц (рис. 24). Чтобы иметь необходимое напряжение на дуге, последовательно с ней включили индуктивную катушку, сопротивление которой
r
=1 Ом.
Определить индуктивность катушки; сопротивление реостата, который можно было бы включить вместо катушки; к.п.д. схемы при наличии в ней катушки и реостата.
Решение:
Полное сопротивление схемы
Полная мощность на входе схемы
Потери мощности в обмотке катушки
Активная мощность схемы
Коэффициент мощности схемы
Из таблиц тригонометрических величин
.
Активное сопротивление схемы
сопротивление дуги
Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:
Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб )
Искомая индуктивность катушки
Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:
Потери мощности в катушке
Потери мощности в реостате
Отсюда ясно, что к. п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки
к. п. д. при наличии реостата
Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере при наличии катушки и при наличии реостата).
22.
Последовательно с катушкой, параметры которой
и L=15,92 мГн, включен реостат сопротивлением,
. Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.
Решение:
Индуктивное сопротивление катушки
Полное сопротивление катушки
Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,
Полное сопротивление цепи
На основании закона Ома ток в цепи
Напряжение на катушке
Напряжение на реостате
Арифметическая сумма много больше приложенного напряжения U=130 В. Коэффициент мощности цепи
Коэффициент мощности катушки
Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки
активная мощность реостата
Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис. 26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора
в сторону опережения вектора тока
I
, под углом
в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке
. Векторы
построены так с целью сложения по правилу многоугольника.
Решение:
Индуктивное сопротивление первой катушки
т. е. оно численно равно активному сопротивлению
, что обусловливает отставание тока по фазе от напряжения на 1
/
8 периода (на 45°).
Действительно, тангенс угла сдвига фаз
Индуктивное сопротивление второй катушки
Так как ее активное сопротивление то тангенс угла сдвига фаз
Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений . Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление , отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление , — в вертикальном направлении под прямым углом к .
Полное сопротивление
первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление
, и под прямым углом к нему вверх — отрезок, изображающий сопротивление
. Гипотенуза
се
прямоугольного треугольника означает полное сопротивление
второй катушки.
Из рис. 27 видно, что отрезок
ае
, изображающий полное сопротивление
z
неразветвленной цепи из двух катушек, не равен сумме отрезков
ас
и
се
, т. е.
. Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (,
отрезок
аf
) и индуктивные (, отрезок
ef
) сопротивления катушек.
Гипотенуза
ае
, означающая полное сопротивление z цепи, определяется по теореме Пифагора:
Ток в цепи определяется по закону Ома:
Напряжение на первой катушке
Напряжение на второй катушке
Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока
; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения
; при этом вектор напряжения
Измерение мощности в 3-ф цепях
Выясним, сколько ваттметров нужно включить для измерения активной мощности в трехфазной цепи при любом несимметричном режиме.
На рис. 32 прямоугольником условно показана сколь угодно сложная цепь, питаемая трехфазной линией с нейтральным проводом. Фазные напряжения на входе линии с нейтральным проводом всегда можно приписать трем источникам напряжения (показаны штриховой линией). Из этого следует, что для измерения активной мощности в трехфазной линии с нейтральным проводом нужно включить три ваттметра, как показано на рис. 32 (ваттметры измеряют активные мощности источников напряжения).
В цепи без нейтрального провода (рис. 33) линейные напряжения на входных выводах всегда можно рассматривать получающимися от двух источников напряжения, например, включенных так, как показано штриховой линией на рис. 33.
Следовательно, активная мощность передачи энергии по линии без нейтрального провода может быть измерена двумя ваттметрами. Следует иметь в виду, что возможны такие режимы работы цепи, при которых стрелка того или иного ваттметра отклоняется в обратную сторону, несмотря на правильное включение ваттметра в цепь. Тогда, чтобы сделать отсчет по шкале, нужно изменить подключение обмотки напряжения или обмотки тока соответствующего ваттметра на противоположное. Измеренную после этого мощность следует считать отрицательной. Пример подобного случая приводится ниже.
Выясним зависимость мощности, измеряемой каждым из ваттметров в схеме рис. 33, от сдвига фаз между напряжениями и токами в частном случае симметричного режима. На рис. 34 показана векторная диаграмма токов и напряжений. Линии, соединяющие центр тяжести треугольника напряжений с его вершинами, можно рассматривать как фазные напряжения эквивалентного приемника, соединенного звездой.
На основании схемы включения одноименных выводов ваттметров и руководствуясь векторной диаграммой, можно записать
Как следует из этих выражений, показания ваттметров одинаковы только при φ=0. При φ=60° получаем P2=0, а при φ= -60° имеем P1 = 0. При φ>60° имеем P2 < 0, а при φ<-60° получаем P1 < 0. При имеем P2=—P1. Таким образом, при |φ|>60° стрелка одного из ваттметров отклоняется в обратную сторону.
Схема измерения активной мощности в четыре. Измерение мощности и энергии
Измерение мощности. В цепях постоянного тока мощность можно измерить косвенным методом с помощью амперметра и вольтметра
Р = UI ,
но более точный результат дает измерение мощности электродинамическим ваттметром, которым измеряется мощность независимо от рода тока. Внешний вид (а) и схема включения ваттметра (б) показаны на рис.16. Ваттметр имеет четыре зажима для подключения подвижной и неподвижной катушек в цепь. Неподвижная катушка включается в цепь последовательно и называется токовой катушкой, а подвижная катушка вместе с добавочным
Рис.16.1. Однофазный ваттметр: а -внешний вид; б -схема включения в электрическую цепь переменного тока.
сопротивлением г д — параллельно нагрузке и называется катушкой напряжения. Начало катушек отмечено звездочкой *I и *U, конец токовой катушки 5 А, а конец обмотки напряжения -150V. Так как направление отклонения указательной стрелки ваттметра зависит от взаимного направления токов в катушках, то выводы *I и *U подключаются к источнику тока, а выводы 5 А и 150V-к нагрузке. Ввиду того что выводы *I и *U подключаются к одному и тому же проводу, их можно соединить между собой проводником, что и делается на практике при измерении мощности в цепи постоянного тока и активной мощности в цепи переменного тока.
Измерение энергии. Различают следующие способы контроля расхода электроэнергии: 1. Косвенный способ. В этом случае измеряют косвенные параметры, а расход электроэнергии определяют расчетом. Так например, расход электроэнергии в цепях постоянного тока определяется по формуле:
W = U I t (16.1),
где U — напряжение на приемнике электроэнергии I — ток в приемнике t — время прохождения тока.
Т.о. для измерения расхода электроэнергии параллельно приемнику нужно включить вольтметр и измерить напряжение U , последовательно приемнику включить амперметр и измерить силу тока I . Время — t измеряется с помощью хронометра. Сняв показания с вольтметра, амперметра и хронометра расход электроэнергии определяют по формуле (16.1). В цепях переменного тока расход электроэнергии определяется по формуле (16.2)
W = U I t cosφ (16.2)
Т.о. для косвенного измерения расхода электроэнергии в данном случае, кроме вольтметра, амперметра и хронометра нужно включить фазометр для измерения коэффициента мощности cosφ.
2. Непосредственный способ. Этот способ используется в цепях переменного тока. В этом случае для измерения расхода электроэнергии используется индукционный счетчик электрической энергии. Счетчик представляет собой суммирующий прибор. Основное отличие его от стрелочного прибора состоит в том, что угол поворота его подвижной части не ограничиваемый пружиной, нарастает и показания счетчика суммируются. Каждому обороту подвижной части счетчика соответствует определенное количество израсходованной энергии. Счетчик включается в Рис. 16.2 электрическую цепь также как ваттметр (рис. 16, 1), т.е. его токовая обмотка (3) включается последовательно с нагрузкой и контролирует силу тока в нагрузке, а обмотка напряжения (2) включается параллельно нагрузке и контролирует напряжение на нагрузке. Время контролируется за счет количества оборотов диска.
Ваттметр состоит из двух катушек: неподвижной 1, состоящей из небольшого числа витков толстой проволоки, и подвижной 2, состоящей из большого числа витков тонкой проволоки. При включении ваттметра ток нагрузки проходит через неподвижную катушку, последовательно включенную в цепь, а подвижная катушка включается параллельно потребителю. Для уменьшения потребляемой мощности в параллельной обмотке н уменьшения веса подвижной катушки последовательно с ней включается добавочное сопротивление 3 из манганина. В результате взаимодействия магнитных полей подвижной и неподвижной катушек возникает момент вращения, пропорциональный токам обеих катушек:
т. е. вращающий момент прибора пропорционален мощности, потребляемой в цепи.
Чтобы стрелка прибора отклонялась от нуля вправо, необходимо ток через катушку пропускать в определенном направлении.
Для этого два зажима, указывающие начала обмоток, обозначаются знаком * и электрически соединяются. На шкале ваттметра указываются номинальный ток и номинальное напряжение прибора. Так, например, если на шкале прибора обозначено 5 А и 150 В, то прибор может измерять мощность до 750 Вт. Шкалы некоторых ваттметров градуированы в делениях. Если, например, ваттметр на 5 А и 150 В имеет 150 делений, то цена деления, или постоянная ваттметра, равна 750: 150 = 5 Вт/дел.
Кроме электродинамических ваттметров, для измерения мощности в цепях постоянного тока употребляются также ваттметры ферродинамической системы.
2. Однофазный переменный ток. При включении электродинамического ваттметра в цепь переменного тока магнитные поля подвижной н неподвижной катушек, взаимодействуя между собой, вызовут поворот подвижной катушки. Мгновенный момент вращения подвижной часги прибора пропорционален произведению мгновенных значений токов в обеих катушках прибора. Но вследствие быстрых изменений токов подвижная система не сможет следовать за этими изменениями и момент вращения прибора будет пропорционален средней или активной мощности Следовательно, по углу поворота подвижной части ваттметра можно судить о величине активной мощности, потребляемой цепью.
Для измерения мощности переменного тока пользуются также ваттметрами индукционной системы. На фиг. 362 показана схема включения индукционного ваттметра с вращающимся маг-нитным полем. Последовательная обмогка 1-1, состоящая из небольшого числа витков толстой проволоки, располагается на двух противоположных полюсных выступах и включена последовательно в цепь. Параллельная обмотка 2-2 ваттметра, состоящая из большого числа витков тонкой проволоки, располагается на двух отдельных полюсных выступах. Последовательно с обмоткой 2-2 включается индуктивное сопротивление 3, служащее для полу-
Чения угла сдвига 90° между ее напряжением и током. Тем самым при чисто активной нагрузке получаем сдвиг на угол 90° между токами в последовательной и параллельной обмотках, что является необходимым условием создания вращающегося магнитного поля. При включении прибора это поле, пересекая алюминиевый цилиндр 4, индуктирует в нем вихревые токи, которые, взаимодействуя с полем, создают вращающий момент, воздействующий на подвижную часть прибора. Угол поворота ее при любой нагрузке будет пропорционален активной мощности, потребляемой цепью:
Принципиальная схема индукционного ваттметра с бегущим полем была дана на фиг. 335.
При измерении ваттметром мощности в сетях низкого напряжения с большими токами применяют трансформаторы тока. Для уменьшения разности потенциалов между обмотками ваттметра первичная и вторичная цепи трансформатора тока имеют общую точку. Вторичная обмотка трансформатора не заземляется, так как это означало бы заземление одного провода сети.
Для определения мощности сети Р 1 в этом случае нужно показание ваттметра P 2 умножить на коэффициент трансформации трансформатора тока :
В сетях высокого напряжения при измерении мощности используются измерительные трансформаторы напряжения н тока (фиг. 363).
Так, например, если к ваттметру установлены трансформатор напряжения 6000/100 В и трансформатор тока 150/5 А, а ваттметр показал 80 Вт, то мощность сети будет:
При включении ваттметров (счетчиков) через измерительные
Трансформаторы нужно присоединять эти приборы так, чтобы по обмоткам их проходили токи в том же направлении, как если бы они были непосредственно включены в сеть.
Кроме ваттметра, мощность однофазного переменного тока можно определить по показаниям трех приборов: амперметра, вольтметра и фазометра согласно формуле:
3. Трехфазный переменный ток. При равномерной нагрузке трехфазной системы для измерения мощности пользуются одним однофазным ваттметром, включенным по схеме, показанной на фиг. 364 (а — для соединения звездой; б — для соединения треугольником). По последовательной обмотке ваттметра в этом случае протекает фазный ток, а параллельная обмотка включена к фазному напряжению. Поэтому ваттметр покажет мощность одной фазы. Для получения мощности трехфазной системы нужно показание однофазного ваттметра умножить на три.
При неравномерной нагрузке в четырехпроводной сети трехфазного тока для измерения мощности применяется схема трех ваттметров (фиг. 365). Каждый однофазный ваттметр измеряет мощность одной фазы. Для получения мощности трехфазной системы необходимо взять сумму показаний трех ваттметров.
При переменной нагрузке трудно получить одновременный отсчет показаний трех ваттметров. Кроме того, три однофазных ваттметра занимают много места. Поэтому часто применяют один трехэлементный трехфазный ваттметр, представляющий собой соединение в одном приборе трех однофазных ваттметров.
У трехэлементного электродинамического ваттметра три подвижные параллельные катушки насажены на одну ось, связанную со стрелкой, и общий момент, полученный в результате сложения механических усилий каждой катушки, будет пропорционален мощности, потребляемой в трехфазной сети. В других конструкциях подвижные катушки, расположенные в разных местах, связаны между собой гибкими лентами и передают суммарное усилие на ось со стрелкой.
Активную мощность трехфазной сети при равномерной нагрузке можно определить
При помощи трех приборов: амперметра, вольтметра и фазометра по формуле:
Мощность трехпроводной трехфазной сети при любой нагрузке (равномерной или неравномерной), независимо от способа соединения потребителя (звездой или треугольником), может быть измерена по схеме двух ваттметров.
По первому закону Кирхгофа сумма мгновенных значений токов всех трех фаз равна нулю:
Полученное уравнение показывает, что один из ваттметров надо включить так, чтобы по его токовой катушке протекал ток первой фазы, а катушка напряжения находилась бы под разностью напряжений первой и второй фаз; другой ваттметр следует включить так, чтобы по его токовой катушке протекал ток третьей фазы, а катушка напряжения находилась бы под разностью напряжений третьей и второй фаз.
Сложив показания обоих ваттметров, получим мощность всех трех фаз.
На фиг. 366 показаны три варианта схемы двух ваттметров.
Из схем на фнг. 366 видно, что последовательные обмотки ваттметров включают в любые два линейных провода сети. Начала параллельных обмоток каждого ваттметра подключаются к тому же проводу, в который включена последовательная обмотка ваттметра. Концы параллельных обмоток подключаются к третьему линейному проводу.
При равномерной активной нагрузке (=1) показания ваттметров равны между собой. При не равном единице, показания ваттметров не будут равны. При равном = 0,5, один из ваттметров покажет нуль. При меньшем 0,5, стрелка этого прибора начнет отклоняться влево. Чтобы получить показание прибора, необходимо переключить концы его последовательной или параллельной обмотки.
Для измерения активной мощности трехфазной системы по показаниям двух ваттметров нужно складывать их показания или вычитать из показания одного ваттметра показание другого ваттметра, которое было отрицательным. Схема измерения мощности двумя ваттметрами с помощью измерительных трансформаторов напряжения и тока дана на фиг. 367.
Удобнее измерять мощность при помощи трехфазного ваттметра, в котором совмещены два прибора, включенные по схеме двух ваттметров и действующие на одну общую ось, с которой связана стрелка.
В сетях высокого напряжения трехфазный ваттметр включается при помощи измерительных трансформаторов напряжения и тока.
Мощность, потребляемая нагрузкой в цепи переменного тока, равна среднему по времени произведению мгновенных значений напряжения и тока нагрузки. Если напряжение и ток изменяются синусоидально, то мощность Р можно представить в виде P = UI cosφ, где U и I – эффективные значения напряжения и тока, а φ – фазовый угол (угол сдвига) синусоид напряжения и тока. Если напряжение выражается в вольтах, а ток в амперах, то мощность будет выражена в ваттах. Множитель cosφ, называемый коэффициентом мощности, характеризует степень синхронности колебаний напряжения и тока.
С экономической точки зрения, самая важная электрическая величина – энергия. Энергия W определяется произведением мощности на время ее потребления. В математической форме это записывается как:
Если время измеряется в секундах, напряжение – в вольтах, а ток – в амперах, то энергия W будет выражена в ватт-секундах, т.е. джоулях. Если же время измеряется в часах, то энергия – в ватт-часах. На практике электроэнергию удобнее выражать в киловатт-часах.
С помощью приборов различных систем производят измерения активной (), реактивной () и полной () мощности в цепях постоянного тока, однофазного и трехфазного переменного тока, мгновенные значения мощности, а также количества электричества в широких пределах. При этом диапазон измеряемых мощностей может составлять от долей мкВт до десятков ГВт.
При косвенных измерениях мощности в цепях постоянного тока используют метод вольтметра и амперметра . В этом случае приборы могут быть включены по двум схемам.
Рис. 9.3 Схемы измерения мощности по показаниям вольтметра и амперметра при малых и больших сопротивлениях нагрузки.
Метод прост, надежен, экономичен, но обладает рядом существенных недостатков:
· необходимость снимать показания по двум приборам;
· необходимостью производить вычисления;
· невысокой точностью за счет суммирования погрешностей приборов.
Компенсационный метод применяется тогда, когда требуется высокая точность измерения мощности. С помощью компенсатора поочередно измеряется ток нагрузки и падение напряжения на нагрузке. Для измерения мощности используют электродинамические приборы.
Рис. 9.4 Схема включения электродинамического ваттметра через измерительные трансформаторы тока и напряжения.
В широком диапазоне частот применяются цифровые ваттметры . Они осуществляют автоматический выбор пределов измерений, самокалибровку, имеют внешний интерфейс.
Для измерения мощности в трехфазных цепях используют методы одного, двух и трех ваттметров .
Первый вариант используют для систем с равномерной нагрузкой фаз, одинаковыми углами сдвига фаз между током и напряжением. При этом нагрузка может быть включена по схеме звезды, треугольника.
При асимметричной нагрузке используют методы двух ваттметров. При этом нужно вычислять суммарную мощность с учетом схемы включения приборов. При использовании схемы с тремя ваттметрами для определения потребляемой мощности производят суммирование показаний.
Для измерения мощности в цепях повышенной частоты применяют как прямые, так и косвенные методы с использованием термоэлектрических преобразователей, датчиков Холла, электронные и цифровые ваттметры. Для измерения энергии используют электромеханические и электронные счетчики.
При измерении мощности, частоты сдвига фаз широко используют измерительные механизмы электродинамической системы, так как эти приборы имеют сложную функциональную зависимость:
(9.4)
Если пропускать ток через последовательно включённые катушки, то можно использовать ток и напряжение при включении в цепь одной из катушек, можно обеспечить дополнительный сдвиг фаз. При этом можно измерить активную и реактивную мощность.
Схема включения ваттметра
Из выражения для мощности на постоянном токе видно, что ее можно измерить с помощью амперметра и вольтметра косвенным методом. Однако в этом случае необходимо производить одновременный отсчет по двум приборам и вычисления, усложняющие измерения и снижающие его точность .
Для измерения мощности в цепях постоянного и однофазного переменного тока применяют приборы, называемые ваттметрами, для которых используют электродинамические и ферродинамические измерительные механизмы .
Электродинамические ваттметры выпускают в виде переносных приборов высоких классов точности (0,1 — 0,5) и используют для точных измерений мощности постоянного и переменного тока на промышленной и повышенной частоте (до 5000 Гц). Ферродинамические ваттметры чаще всего встречаются в виде щитовых приборов относительно низкого класса точности (1,5 — 2,5).
Применяют такие ваттметры главным образом на переменном токе промышленной частоты. На постоянном токе они имеют значительную погрешность , обусловленную гистерезисом сердечников.
Для измерения мощности на высоких частотах применяют термоэлектрические и электронные ваттметры, представляющие собой магнитоэлектрический измерительный механизм, снабженный преобразователем активной мощности в постоянный ток. В преобразователе мощности осуществляется операция умножения и получение сигнала на выходе, зависящего от произведения UI , т. е. от мощности.
Рис. 8.3.
Если не учитывать фазовых сдвигов между токами и напряжениями в катушках и считать нагрузку H чисто активной, погрешности и , обусловленные потреблением мощности катушками ваттметра, для схем (рис. 8.3):
где и – соответственно мощность , потребляемая последовательной и параллельной цепью ваттметра.
Из формул для и видно, что погрешности могут иметь заметные значения лишь при измерениях мощности в маломощных цепях, т. е. когда и соизмеримы с .
Если поменять знак только одного из токов, то изменится направление отклонения подвижной части ваттметра.
У ваттметра имеются две пары зажимов (последовательной и параллельной цепей), и в зависимости от их включения в цепь направление отклонения указателя может быть различным. Для правильного включения ваттметра один из каждой пары зажимов обозначается знаком «*» (звездочка) и называется «генераторным зажимом».
Измерение мощности с использованием эффекта Холла
Перемножение значений силы тока и разности потенциалов при измерении мощности можно получить, используя полупроводниковые преобразователи Холла.
Если специальную полупроводниковую пластину, по которой течет ток I (рис. 8.4), возбуждаемый электрическим полем напряженностью Е, поместить в магнитное поле с напряженностью Н (индукцией В), то между ее точками, лежащими на прямой , перпендикулярной направлениям протекающего тока I и магнитного поля, возникает разность потенциалов (эффект Холла), определяемая как
где k – коэффициент пропорциональности.
Рис. 8.4.
Согласно теореме Умова-Пойнтинга, плотность потока проходящей мощности СВЧ-колебаний в некоторой точке поля определяется векторным произведением электрической и магнитной напряженностей этого поля:
Отсюда, если ток I будет функцией электрической напряженности Е, то с помощью датчика Холла можно получить следующую зависимость напряжения от проходящей мощности:
где g – постоянный коэффициент, характеризующий образец. Для измерения такой мощности пластину полупроводника (пластинку Холла – ПХ) помещают в волновод, как показано (рис. 8.5).
Рис. 8.5.
Рассмотренный измеритель проходящей мощности обладает следующими достоинствами:
- может работать при любой нагрузке, а не только при согласованной;
- высокое быстродействие ваттметра дает возможность применять его при измерении импульсной мощности.
Однако практическая реализация ваттметров на эффекте Холла – достаточно сложная задача в силу многих факторов. Тем не менее, существуют ваттметры, измеряющие проходящую импульсную мощность до 100 кВт с погрешностью не более 10 %.
Методы измерения мощности на высоких и сверхвысоких частотах
Мощность в общем виде есть физическая величина, которая определяется работой, производимой в единицу времени. Единица мощности – ватт (Вт) – соответствует мощности, при которой за одну секунду выполняется работа в один джоуль (Дж).
На постоянном токе и переменном токе низкой частоты непосредственное измерение мощности зачастую заменяется измерением действующего значения электрического напряжения на нагрузке U , действующего значения тока, протекающего через нагрузку I , и угла сдвига фаз между током и напряжением . При этом мощность определяют выражением:
В СВЧ диапазоне измерение напряжения и тока становится затруднительным. Соизмеримость размеров входных цепей измерительных устройств с длиной волны является одной из причин неоднозначности измерения напряжения и тока.
Измерения сопровождаются значительными частотными погрешностями. Следует добавить, что измерение напряжения и тока в волноводных трактах при некоторых типах волн теряет практический смысл, так как продольная составляющая в проводнике отсутствует, а разность потенциалов между концами любого диаметра сечения волновода равна нулю. Поэтому на частотах, начиная с десятков мегагерц, предпочтительным и более точным становится непосредственное измерение мощности, а на частотах свыше 1000 МГц – это единственный вид измерений, однозначно характеризующий интенсивность электромагнитных колебаний.
Для непосредственного измерения мощности СВЧ применяют методы, основанные на фундаментальных физических законах, включающие метод прямого измерения основных величин: массы, длины и времени.
Несмотря на разнообразие методов измерения СВЧ мощности, все они сводятся к преобразованию энергии электромагнитных СВЧ колебаний в другой вид энергии, доступной для измерения: тепловую, механическую и т. д. Среди приборов для измерения СВЧ мощности наибольшее распространение получили ваттметры, основанные на тепловых методах. Используют также ряд других методов – пондеромоторный, зондовый и другие.
Принцип действия подавляющего большинства измерителей мощности СВЧ, называемых ваттметрами, основан на измерении изменений температуры или сопротивления элементов, в которых рассеивается энергия исследуемых электромагнитных колебаний. К приборам, основанным на этом явлении, относятся калориметрические и терморезисторные измерители мощности. Получили распространение ваттметры, использующие пондеромоторные явления (электромеханические силы), и ваттметры, работающие на эффекте Холла. Особенность первых из них – возможность абсолютных измерений мощности, а вторых – измерение мощности независимо от согласования ВЧ-тракта.
По способу включения в передающий тракт различают ваттметры проходящего типа и поглощающего типа. Ваттметр проходящего типа представляет собой четырехполюсник, в котором поглощается лишь небольшая часть общей мощности. Ваттметр поглощающего типа, представляющий собой двухполюсник, подключается на конце передающей линии, и в идеальном случае в нем поглощается вся мощность падающей волны. Ваттметр проходящего типа часто выполняется на основе измерителя поглощающего типа, включенного в тракт через направленный ответвитель.
Калориметрические методы измерения мощности основаны на преобразовании электромагнитной энергии в тепловую в сопротивлении нагрузки, являющейся составной частью измерителя. Количество выделяемого тепла определяется по данным изменения температуры в нагрузке или в среде, куда передано тепло. Различают калориметры статические (адиабатические) и поточные (неадиабатические). В первых мощность СВЧ рассеивается в термоизолированной нагрузке, а во вторых предусмотрено непрерывное протекание калориметрической жидкости. Калориметрические измерители позволяют измерять мощность от единиц милливатт до сотен киловатт. Статические калориметры измеряют малый и средний уровни мощности, а поточные – средние и большие значения мощности
Условие баланса тепла в калориметрической нагрузке имеет вид:
где P – мощность СВЧ, рассеиваемая в нагрузке; T и T 0 – температура нагрузки и окружающей среды соответственно; c , m – удельная теплоемкость и масса калориметрического тела; k – коэффициент теплового рассеяния. Решение уравнения представляется в виде
где – тепловая постоянная времени.
В случае статического калориметра время измерения много меньше постоянной и мощность СВЧ равна:
Основными элементами статических калориметров являются термоизолированная нагрузка и прибор для измерения температуры. Нетрудно рассчитать поглощаемую мощность СВЧ по измеренной скорости повышения температуры и известной теплоемкости нагрузки.
В приборах используются различные высокочастотные оконечные нагрузки из твердого или жидкого диэлектрического материала с потерями, а также в виде пластинки или пленки высокого сопротивления. Для определения изменения температуры применяют термопары и различные термометры.
Рассмотрим статический калориметр, в котором снижены требования к термоизоляции и отпадает необходимость в определении теплоемкости калориметрической насадки (рис. 8.6). В этой схеме используется метод замещения. В ней для калибровки прибора 4, измеряющего повышение температуры при рассеянии измеряемой мощности, подводимой к плечу 1, используется известная мощность постоянного тока или тока низкой частоты, подводимая к плечу 2. Предполагается, что температура насадки 3 изменяется одинаково при рассеянии равных значений мощности СВЧ и постоянного тока. Статические калориметры позволяют измерять мощность несколько милливатт с погрешностью менее .
Измерение мощности производят обычно с помощью ваттметра электродинамической системы, в котором имеются две катушки — неподвижная и подвижная.
Подвижная катушка, выполненная из очень тонкого провода, имеет практически чисто активное сопротивление и называется параллельной обмоткой. Ее включают параллельно участку цепи, подобно вольтметру. Жестко скрепленная со стрелкой (указателем), она может вращаться в магнитном поле, создаваемом непод вижной катушкой.
Неподвижная катушка, выполненная из довольно толстого провода, имеет очень малое активное сопротивление и называется последовательной обмоткой. Ее включают в цепь последовательно, подобно амперметру.
На электрической схеме ваттметр изображают, как показано на рис. 3.22. Одна пара концов (на рисунке обычно расположена горизонтально) принадлежит последовательной обмотке, другая пара концов (на рисунке расположена вертикально) — параллельной. На концах одноименных зажимов обмоток (например, у начала обмоток) принято ставить точки.
Вращающий момент ваттметра, а следовательно, и его показания пропорциональны действительной части произведения комплексного напряжения на параллельной обмотке ваттметра на сопряженный комплекс тока втекающего в конец последовательной (токовой) обмотки ваттметра и снабженной точкой:
Напряжение на параллельной обмотке берут равным разности потенциалов между ее концом, имеющим точку (точка а), и ее концом, не имеющим точки (точка ). Предполагается, что ток втекает в конец последовательной обмотки, у которого поставлена точка.
Цена деления ваттметра определяется как частное от деления произведения номинального напряжения на номинальный ток (указывают на лицевой стороне прибора) на число делений шкалы.
Пример 41. Номинальное напряжение ваттметра 120 В. Номинальный ток 5 А. Шкала имеет 150 делений. Определить цену деления ваттметра.
Решение. Цена деления ваттметра равна
Для непосредственного измерения мощности цепи постоянного тока применяется ваттметр. Неподвижная последовательная катушка или катушка тока ваттметра соединяется последовательно с приемниками электрической энергии. Подвижная параллельная катушка или катушка напряжения, соединенная последовательно с добавочным сопротивлением, образует параллельную цепь ваттметра, которая присоединяется параллельно приемникам энергии.
Угол поворота подвижной части ваттметра:
α = k2IIu = k2U/Ru
где I
— ток последовательной катушки; I
и — ток параллельной катушки ваттметра.
Рис. 1. Схема устройства и соединений ваттметра
Так как в результате применения добавочного сопротивления параллельная цепь ваттметра имеет практически постоянное сопротивление ru , то α = (k2/Ru)IU = k2IU = k3P
Таким образом, по углу поворота подвижной части ваттметра можно судить о мощности цепи.
Шкала ваттметраравномерна. При работе с ваттметром необходимо иметь в виду, что изменение направления тока в одной из катушек вызывает изменение направления вращающего момента и направления поворота подвижной катушки, а так как обычно шкала ваттметра делаетсяодносторонней, т. е. деления шкалы расположены от нуля вправо, то при неправильном направлении тока в одной из катушек определение измеряемой величины по ваттметру будет невозможно.
По указанным причинам следует всегда различать зажимы ваттметра. Зажим последовательной обмотки, соединяемый с источником питания, называется генераторным и отмечается на приборах и схемах звездочкой. Зажим параллельной цепи, присоединяемый к проводу, соединенному с последовательной катушкой, также называется генераторным и отмечается звездочкой.
Таким образом, при правильной схеме включения ваттметра токи в катушках ваттметра направлены от генераторных зажимов к негенераторным. Могут иметь место две схемы включения ваттметра (см. рис. 2 и рис. 3).
Рис. 2. Правильная схема включения ваттметра
Рис. 3. Правильная схема включения ваттметра
В схеме, данной на рис. 2, ток последовательной обмотки ваттметра равен току приемников энергии, мощность которых измеряется, а параллельная цепь ваттметра находится под напряжением U» большим, чем напряжение приемников, на величину падения напряжения в последовательной катушке. Следовательно, Рв = IU» = I(U+U1) = IU = IU1 , т. е. мощность, измеряемая ваттметром, равна мощности приемников энергии, подлежащей измерению, и мощности последовательной обмотки ваттметра.
В схеме, данной на рис. 3, напряжение на параллельной цепи ваттметра равно напряжению на приемниках, а ток в последовательной обмотке больше тока, потребляемого приемником, на величину тока параллельной цепи ваттметра. Следовательно, P в = U(I+Iu) = UI+ UIu , т. е. мощность, измеряемая ваттметром, равна мощности приемников энергии, подлежащей измерению, и мощности параллельной цепи ваттметра.
При измерениях, в которых мощностью обмоток ваттметра можно пренебречь, предпочтительнее пользоваться схемой, показанной на рис. 2, так как обычно мощность последовательной обмотки меньше, чем параллельной, а следовательно, показания ваттметра будут более точными.
При точных измерениях необходимо вводить поправки в показания ваттметра, обусловленные мощностью его обмотки, и в таких случаях можно рекомендовать схему на рис.3, так как поправка легко вычисляется по формуле U 2 /Ru , где Ru обычно известно, а поправка остается неизменной при различных значениях тока, если U постоянно.
При включении ваттметра по схеме на рис. 2 потенциалы концов катушек разнятся только на величину падения напряжения в подвижной катушке, так как генераторные зажимы катушек соединены вместе. Падение напряжения в подвижной катушке незначительно по сравнению с напряжением на параллельной цепи, так как сопротивление этой катушки незначительно по сравнению с сопротивлением параллельной цепи.
Рис. 4. Неправильная схема включения ваттметра
На рис. 4 дана неправильная схема включения параллельной цепи ваттметра. Здесь генераторные зажимы катушек соединены через добавочное сопротивление, вследствие чего разность потенциалов между концами катушек равна напряжению цепи (иногда весьма значительному 240 — 600 В), а так как неподвижная и подвижная катушки находятся в непосредственной близости одна от другой, то создаются условия, благоприятные для пробоя изоляции катушек. Кроме того, между катушками, имеющими весьма различные потенциалы, будет наблюдаться электростатическое взаимодействие, могущее вызвать дополнительную погрешность при измерении мощности в электрической цепи.
В настоящее время необходимо измерять мощность и энергию постоянного тока, активную мощность и энергию переменного однофазного и трехфазного тока, реактивную мощность и энергию трехфазного переменного тока, мгновенное значение мощности, а также количество электричества в очень широких пределах.
Электрическая мощность определяется работой, совершаемой источником электромагнитного поля в единицу времени.
Активная (поглощаемая электрической цепью) мощность
P a =UIcos > = I 2 R=U 2 /R, (1)
где U , I — действующие значения напряжения и тока; — угол сдвига фаз.
Реактивная мощность
Р р = UIsin = I 2 X . (2)
Полная мощность
P n = UI = PZ . Эти три типа мощности связаны выражением
P =(Р а 2 +Р 2 р ) (3)
Так, мощность измеряется в пределах 1 Вт… 10 ГВт (в цепях постоянного и однофазного переменного тока) с погрешностью ±(0,01…0,1) %, а при СВЧ — с погрешностью ±(1…5) %. Реактивная мощность от единиц вар до Мвар измеряется с погрешностью ±(0,1…0,5)%.
Диапазон измерения электрической энергии определяется диапазонами измерения номинальных токов (1 нА…1О кА) и напряжений (1 мкВ…1 MB), погрешность измерения составляет ±(0,1…2,5)%.
Измерение реактивной энергии представляет интерес только для промышленных трехфазных цепей.
Измерение мощности в цепях постоянного тока. При косвенном измерении мощности используют метод амперметра и вольтметра и компенсационный метод.
Метод амперметра и вольтметра. В этом случае приборы включаются по двум схемам (рис.1).
Метод прост, надежен, экономичен, но обладает рядом существенных недостатков: необходимостью снимать показания по двум
Рис. .1. Схемы измерения мощности по показаниям вольтметра и амперметра при малых (а) и больших (б) сопротивлениях нагрузки
приборам; необходимостью производить вычисления; невысокой точностью за счет суммирования погрешности приборов.
Мощность Р х , вычисленная по показаниям приборов (рис. 1а), имеет вид
Она больше действительного значения мощности, расходуемой в нагрузке Р н, на значение мощности потребления вольтметра Р v , т. е. Р н = Р х – Р v .
Погрешность определения мощности в нагрузке тем меньше, чем больше входное сопротивление вольтметра и меньше сопротивление нагрузки.
Мощность Р х , вычисленная по показаниям приборов (рис 1., б), имеем вид
Она больше действительного значения мощности потребления нагрузки на значение мощности потребления амперметром Р А . Методическая погрешность тем меньше, чем меньше входное сопротивление амперметра и больше сопротивление нагрузки.
Компенсационный метод. Этот метод применяется тогда, когда требуется высокая точность измерения мощности. С помощью компенсатора поочередно измеряется ток нагрузки и падение напряжения на нагрузке. Измеряемая мощность определяется по формуле
P = U н I н . (4)
При прямом измерении активная мощность измеряется электромеханическими (электродинамической и ферродинамической систем), цифровыми и электронными ваттметрами.
Электродинамические ваттметры применяются как переносные приборы для точных измерений мощности (класс 0,1… 2,5) в цепях постоянного и переменного тока с частотой до нескольких тысяч герц.
Ферродинамические щитовые вольтметры применяются в цепях переменного тока промышленной частоты (класс 1,5…2,5).
В широком диапазоне частот применяются цифровые ваттметры, основу
составляют различные преобразователи мощности (например, термоэлектрические), УПТ, микропроцессор и ЦОУ. В цифровых ваттметрах осуществляется автоматический выбор пределов измерений, самокалибровка и предусмотрен внешний интерфейс.
Для измерения мощности в высокочастотных цепях также используются специальные и электронные ваттметры.
Для измерения реактивной мощности на низких частотах служат реактивные ваттметры (варметры), в которых путем использования специальных схем отклонение подвижной части электродинамического ИМ пропорционально реактивной мощности.
Включение электромеханических ваттметров непосредственно в электрическую цепь допустимо при токах нагрузки, не превышающих 10… 20 А, и напряжениях до 600 В. Измерение мощности при больших токах нагрузки и в цепях высокого напряжения производится ваттметром с измерительными трансформаторами тока ТА и напряжения TV (рис..2).
Измерение активной мощности в цепях трехфазного тока. Метод одного ваттметра. Этот метод применяется только в симметричной системе с равномерной нагрузкой фаз, одинаковыми углами сдвига по фазе между векторами I и U и с полной симметрией напряжений (рис..3).
Рис..3. Схемы включения ваттметра в трехфазную трехпроводную цепь при полной симметрии присоединения нагрузки:
а — звездой; б — треугольником; в ~- с искусственной нулевой точкой
Рис.4. Схемы включения двух ваттметров в трехфазную цепь: а — в 1-ю и 3-ю; б — в 1-ю и 2-ю; в — в 2-ю и 3-ю
На рис. .3, а нагрузка соединена звездой и нулевая точка доступна. На рис.3, б нагрузка соединена треугольником, ваттметр включен в фазу. На рис. .3, в нагрузка соединена треугольником с искусственной нулевой точкой. Искусственная нулевая точка создается с помощью двух резисторов, каждый из которых равен сопротивлению цепи обмотки напряжения ваттметра (обычно указывается в техническом паспорте на ваттметр).
Показания ваттметра будут соответствовать мощности одной фазы, а мощность всей трехфазной сети во всех трех случаях включения прибора будет равна мощности одной фазы, умноженной на три:
Р = 3 P w
Метод двух ваттметров. Этот метод применяется в трехфазной трехпроводной цепи независимо от схемы соединения и характера нагрузки как при симметрии, так и при асимметрии токов и напряжений. Асимметрия — это система, в которой мощности отдельных фаз различны. Токовые обмотки ваттметров включаются в любые две фазы, а обмотки напряжения включаются на линейные напряжения (рис. 4).
Полная мощность может быть выражена в виде суммы показаний Двух ваттметров. Так, для схемы, представленной на рис..4, а,
где 1 — угол сдвига фаз между током I 1 и линейным напряжением U 12, 2 — угол сдвига фаз между током I 3 и линейным напряжением U 32 . В частном случае при симметричной системе напряжений и одинаковой нагрузке фаз 1 , = 30° — и 2 = 30° — показания ваттметров будут:
При активной нагрузке (= 0) показания ваттметров будут одинаковы, так как P W ] = P W 2 IUcos 30°.
При нагрузке с углом сдвига ср = 60° показания второго ваттметра равны нулю, так как P W 2 = IU cos(30° + ) = IU cos(30° + 60°) = 0, и в этом случае мощность трехфазной цепи измеряется одним ваттметром.
При нагрузке с углом сдвига > 60° мощность, измеряемая вторым ваттметром, будет отрицательной, так как (30° +) больше 90°. В этом случае подвижная часть ваттметров повернется в обратную сторону. Для отсчета необходимо изменить на 180° фазу тока в одной из цепей ваттметра. В этом случае мощность цепи трехфазного тока равна разности показаний ваттметров
Метод трех ваттметров. Для измерения мощности трехфазной цепи при несимметричной нагрузке включаются три ваттметра, и общая мощность при наличии нулевого провода будет равна арифметической сумме показаний трех ваттметров. В этом случае каждый ваттметр измеряет мощность одной фазы, показания ваттметра независимо от характера нагрузки будут положительные (параллельная обмотка включается на фазное напряжение, т. е. между линейным проводом и нулевым). Если нулевая точка недоступна и нулевой провод отсутствует, то параллельные цепи приборов могут образовать искусственную нулевую точку при условии, что сопротивления этих цепей равны между собой.
Измерение реактивной мощности в однофазных и трехфазных цепях. Несмотря на то что реактивная мощность не определяет ни совершаемой работы, ни передаваемой энергии за единицу времени, ее измерение также важно. Наличие реактивной мощности приводит к дополнительным потерям электрической энергии в линиях передачи, трансформаторах и генераторах. Реактивная мощность измеряется в вольт-амперах реактивных (вар) как в однофазных, так и в трехфазных трех- и четырехпроводных цепях переменного тока электродинамическими и ферродинамическими или специально предназначенными для измерения реактивной мощности ваттметрами. Отличие реактивного ваттметра от обычного состоит в том, что он имеет усложненную схему параллельной цепи для получения сдвига по фазе, равного 90°
между векторами тока и напряжения этой цепи. Тогда отклонение подвижной части будет пропорционально реактивной мощности Р р = UIsin . Реактивные ваттметры преимущественно применяются для лабораторных измерений и поверки реактивных счетчиков.
Реактивную мощность в трехфазной симметричной цепи можно измерить и активным ваттметром: для этого –токовая катушка последовательно включается в фазу А, катушка напряжения между фазами В и С.
Измерение мощности в цепях повышенной частоты. С этой целью можно использовать как прямые, так и косвенные измерения и в ряде случаев предпочтительнее могут оказаться косвенные, так как иногда легче измерить ток и напряжение на нагрузке, чем непосредственно мощность. Прямое измерение мощности в цепях повышенных и высоких частот производится термоэлектрическими, электронными ваттметрами, ваттметрами, основанными на эффекте Холла, и цифровыми ваттметрами.
Косвенные измерения осуществляются осциллографическим методом. Он применяется в основном тогда, когда цепь питается напряжением несинусоидальной формы, при высоких частотах, маломощных источниках напряжения и т. д.
Измерение энергии в однофазных и трехфазных цепях. Энергия измеряется электромеханическими и электронными счетчиками электрической энергии. Электронные счетчики электрической энергии обладают лучшими метрологическими характеристиками, большей надежностью и являются перспективными средствами измерений электрической энергии.
4. Измерение фазы и частоты
Фаза характеризует состояние гармонического сигнала в определенный момент времени t . Фазовый угол в начальный момент времени (начало отсчета времени), т.е. при t = 0, называют нуле вым (начальным) фазовым сдвигом. Разность фаз измеряют обычно между током и напряжением либо между двумя напряжениями. В первом случае чаще интересуются не самим углом сдвига фаз, а величиной cos или коэффициентом мощности. Cos- это косинус того угла, на который опережает или отстает ток нагрузки от напряжения, приложенного к этой нагрузке. Фазовым сдвигом двух гармонических сигналов одинаковой частоты называют модуль разности их начальных фаз =| 1 — 2 |. Фазовый сдвиг не зависит от времени, если остаются неизменными начальные фазы 1 , и 2 . Разность фаз выражается в радианах или градусах.
Методы измерения угла сдвига фаз. Эти методы зависят от диапазона частот, уровня и формы сигнала, от требуемой точности и Наличия средств измерений. Различают косвенное и прямое изменения угла сдвига фаз.
Косвенное измерение. Такое измерение угла сдвига фаз Между напряжением U и током I в нагрузке в однофазных цепях
осуществляют с помощью трех приборов — вольтметра, амперметра и ваттметра (рис.5). Угол определяется расчетным путем из найденного значения cos:
Метод используется обычно на промышленной частоте и обеспечивает невысокую точность из-за методической погрешности, вызванной собственным потреблением приборов, достаточно прост, надежен, экономичен.
В трехфазной симметричной цепи величина cos может быть определена следующими измерениями:
мощность, ток и напряжение одной фазы;
измерение активной мощности методом двух ваттметров;
измерение реактивной мощности методом двух ваттметров с искусственной нейтральной точкой.
Среди осциллографических методов измерения фазы наибольшее распространение получили методы линейной развертки и эллипса. Осциллографический метод, позволяющий наблюдать и фиксировать исследуемый сигнал в любой момент времени, используется в широком диапазоне частот в маломощных цепях при грубых измерениях (5… 10 %). Метод линейной развертки предполагает применение двухлучевого осциллографа, на горизонтальные пластины которого подают линейное развертывающее напряжение, а на вертикальные пластины — напряжение, между которыми измеряется фазовый сдвиг. Для синусоидальных кривых на экране получаем изображение двух напряжений (рис.6, а) и по измеренным отрезкам АБ и АС вычисляется угол сдвига между ними
где АБ — отрезок между соответствующими точками кривых при переходе их через нуль по оси X ; АС — отрезок, соответствующий периоду.
Погрешность измерения х зависит от погрешности отсчета и фазовой погрешности осциллографа.
Если вместо линейной развертки использовать синусоидальное развертывающее напряжение, то получаемые на экране фигуры Лиссажу при равных частотах дают на экране осциллографа форму эллипса (Рис. 6б). Угол сдвига x =arcsin(АБ/ВГ).
Этот метод позволяет измерять х в пределах 0 90 о без определения знака фазового угла.
Погрешность измерения х также определяется погрешностью отсчета
Рис..6. Кривые, получаемые на экране двухлучевого осциллографа: при линейной (а) и синусоидальной (б) развертке
и расхождениями в фазовых сдвигах каналов Х и Y осциллографа.
Применение компенсатора переменного тока с калиброванным фазовращателем и электронным осциллографом в качестве индикатора равенства фаз позволяет произвести достаточно точное измерение угла сдвига фаз. Погрешность измерения в этом случае определяется в основном погрешностью используемого фазовращателя.
Прямое измерение. Прямое измерение утла сдвига фаз осуществляют с помощью электродинамических, ферродинамических, электромагнитных, электронных и цифровых фазометров. Наиболее часто из электромеханических фазометров используют электродинамические и электромагнитные логометрические фазометры. Шкала у этих приборов линейная. Используются на диапазоне частот от 50 Гц до 6… 8 кГц. Классы точности — 0,2; 0,5. Для них характерна большая потребляемая мощность 1(5…10 Вт).
В трехфазной симметричной цепи измерение угла сдвига фаз или cos осуществляется однофазным или трехфазным фазометрами.
Цифровые фазометры используются в маломощных цепях в диапазоне частот от единиц Гц до 150 МГц, классы точности — 0,005; 0,01; 0,02; 0,05; 0,1; 0,5; 1,0. В электронно-счетных цифровых фазометрах сдвиг по фазе между двумя напряжениями преобразуется во временной интервал, заполняемый импульсами стабильной частоты с определенным периодом, которые под-считываются электронным счетчиком импульсов. Составляющие погрешности этих приборов: погрешность дискретности, погрешность генератора стабильной частоты, погрешность, зависящая от точности формирования и передачи временного интервала.
Методы измерения частоты. Частота является одной из важнейших характеристик периодического процесса. Определяется числом полных циклов (периодов) изменения сигнала в единицу времени. Диапазон используемых в технике частот очень велик и колеблется от долей герц до десятков. Весь спектр частот подразделяется на два диапазона — низкие и высокие.
Низкие частоты: инфразвуковые — ниже 20 Гц; звуковые — 20…20000 Гц; ультразвуковые — 20…200 кГц.
Высокие частоты: высокие — от 200 кГц до 30 МГц; ультравысокие — 30…300 МГц.
Поэтому выбор метода измерения частоты зависит от диапазона измеряемых частот, необходимой точности измерения, величины и формы напряжения измеряемой частоты, мощности измеряемого сигнала, наличия средств измерений и т.д.
Прямое измерение. Метод основан на применении электромеханических, электронных и цифровых частотомеров.
Электромеханические частотомеры используют измерительный механизм электромагнитной, электродинамической и ферродинамической систем с непосредственным отсчетом частоты по шкале логометрического измерителя. Они просты в устройстве и эксплуатации, надежны, обладают довольно высокой точностью. Их используют в диапазоне частот от 20 до 2500 Гц. Классы точности — 0,2; 0,5; 1,0; 1,5; 2,5.
Электронные частотомеры применяются при измерениях в частотном диапазоне от 10 Гц до нескольких мегагерц, при уровнях входного сигнала 0,5… 200 В. Они имеют большое входное сопротивление, что обеспечивает малое потребление мощности. Классы точности — 0,5; 1,0 и ниже.
Цифровые частотомеры применяются для очень точных измерений в диапазоне 0,01 Гц… 17 ГГц. Источниками погрешности являются погрешность от дискретности и нестабильности кварцевого генератора.
Мостовой метод. Этот метод измерения частоты основан на использовании частотозависимых мостов переменного тока, питаемых напряжением измеряемой частоты. Наиболее распространенной мостовой схемой для измерения частоты является емкостной мост. Мостовой метод измерения частоты применяют для измерения низких частот в пределах 20 Гц… 20 кГц, погрешность измерения составляет 0,5… 1 %.
Косвенное измерение. Метод осуществляется с использованием осциллографов: по интерференционным фигурам (фигурам Лиссажу) и круговой развертки. Методы просты, удобны и достаточно точны. Их применяют в широком диапазоне частот 10 Гц… 20 МГц. Недостатком метода Лиссажу является сложность расшифровки фигур при соотношении фигур более 10 и, следовательно, возрастает погрешность измерения за счет установления истинного отношения частот. При методе круговой развертки погрешность измерения в основном определяется погрешностью квантования основной частоты.
МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ ПАРАМЕТРОВ ИЗМЕРИТЕЛЬНЫХ ЦЕПЕЙ
Что такое ваттметр?
Ваттметр — это прибор, который дает визуальную индикацию количества электроэнергии, подаваемой в цепь. Этот показатель выражается в ваттах, которые являются стандартной единицей измерения подачи или потребления электроэнергии. Обычно используются два типа ваттметров: аналоговые и цифровые. Аналоговые измерители показывают источник питания с помощью стрелки и индикатора шкалы, в то время как цифровые инструменты отображают потребление энергии на жидкокристаллическом дисплее (ЖКД).Ваттметры обычно рассчитаны на заданный диапазон напряжений, но могут включать в себя такие функции, как отводы катушки, которые допускают несколько напряжений.
Все электрическое оборудование потребляет мощность в соответствии с набором известных констант, которые включают номинальное напряжение, потребление тока, выраженное в амперах, и общее потребление энергии, выраженное в ваттах.Некоторые типы электроприборов или установок потребляют гораздо больше энергии, чем другие с аналогичным номинальным напряжением. Ваттметр позволяет контролировать потребление энергии, чтобы установить, правильно ли работают цепи. Эта информация имеет решающее значение в более крупных установках, где используются большие резистивные нагрузки. Ваттметры в таких установках позволяют операторам и техническим специалистам отслеживать состояние отдельных цепей, а также общую балансировку и потребление электроэнергии.
Ваттметры обычно представлены в одном из двух основных форматов.Первый — это традиционный аналоговый ваттметр. Эти электродинамические инструменты состоят из трех внутренних катушек — двух катушек статического тока и подвижной катушки потенциала, к которой прикреплена индикаторная стрелка. Когда электрический ток проходит через две токовые катушки, создается электромагнитное поле. Это поле заставляет катушку потенциала перемещаться и отображать значение на шкале за иглой.
Второй тип ваттметров — это электронный или цифровой измеритель.Эти устройства отличаются от электродинамических счетчиков способом расчета потребляемой мощности. Цифровые измерители используют микропроцессор для оценки значений напряжения и силы тока в цепи с частотой несколько тысяч выборок в секунду. Эти образцы используются для расчета среднего коэффициента мощности или энергопотребления. Затем значение коэффициента мощности отображается в цифровом виде на ЖК-дисплее.
Ваттметр является довольно чувствительным прибором и может выйти из строя из-за чрезмерных значений тока.Как и большинство электрических измерительных приборов, ваттметры обычно рассчитаны на определенный диапазон напряжений. Многие высокопроизводительные счетчики имеют отводы катушек или переключение катушек последовательного / параллельного тока, что позволяет использовать такие устройства для нескольких диапазонов напряжения. Все ваттметры также рассчитаны на безопасные значения максимального тока или силы тока; эти характеристики следует соблюдать во избежание повреждения или разрушения счетчика.
Ваттметр (простой измеритель мощности переменного тока)
Ваттметр (простой измеритель мощности переменного тока)
Введение:
Ваттметр — важный измерительный прибор.Это позволяет измерить истинную электрическую мощность (мощность).
Определить истинную мощность в цепях переменного тока невозможно простым умножением действующего значения напряжения и тока, поскольку
коэффициент мощности часто не равен 1. Вы должны использовать счетчик, который непрерывно измеряет
мгновенный ток и напряжение, умножает их и выдает среднее значение. Это делают аналоговые электромеханические устройства.
с помощью катушки тока (сплошной) и катушки напряжения (подвижной, с прикрепленной к ней иглой). Магнитная сила, действующая между катушками, равна произведению
магнитных полей.Усреднение достигается за счет импульса системы. Традиционные ваттметры с аналоговой шкалой не очень точны и обычно имеют низкий полезный диапазон измерения.
Теория электронного ваттметра:
Я решил сделать это твердотельным способом — построить электронный измеритель мощности с аналоговой обработкой и цифровым считыванием.
Дисплей снабжен цифровым мультиметром, который сейчас можно купить менее чем за 100 крон (примерно 4 доллара США), поэтому нет смысла строить свой собственный.
цифровой вольтметр.Также можно использовать панельный цифровой вольтметр или даже аналоговый измеритель.
Непосредственное напряжение измеряется с помощью делителя напряжения. Ток измеряется шунтом. Затем напряжение и ток умножаются аналоговым умножителем AD633.
Выход обеспечивает напряжение, пропорциональное мгновенной мощности. Для получения средней мощности необходимо отфильтровать сигнал с помощью RC-фильтра.
Самая большая проблема в этой конструкции — создание произведения двух аналоговых напряжений.Это не так просто
может показаться. Есть возможность умножения с использованием операционных усилителей и переходов дискретных диодов или транзисторов, имеющих экспоненциальную характеристику.
Их принцип состоит в том, чтобы логарифмировать оба сигнала, складывать их и, наконец, делать логарифмы. Точность не слишком хорошая, есть проблемы с калибровкой, огромная
температурная зависимость и различия между отдельными частями транзисторов или диодов. Поэтому я отказался от этого варианта. Другой вариант —
с использованием широтно-импульсных умножителей, но это решение тоже весьма своеобразно.Еще больше сложностей возникает, когда надо работать
с обеими полярностями тока и напряжения (4 квадранта). Поэтому я решил использовать специализированную интегральную схему AD633 (AD633JN в классическом корпусе THT DIP8) —
четырехквадрантный аналоговый умножитель с дифференциальными входами и точностью 2%. Для получения дополнительной информации см. Техническое описание AD633.
Обратите внимание, что версия SMD имеет другую распиновку!
Выходное напряжение определяется формулой:
w = (x2-x1) * (y1-y2): 10 В + z
Хотел попробовать микросхему MPY634 с точностью до 0.5%, но найти не удалось.
Максимальный диапазон входного и выходного напряжения, при котором работает схема AD633, составляет +/- 10В. Это должно соответствовать обоим входным напряжениям.
Схема должна быть рассчитана на амплитуду тока и напряжения, а не только на действующее значение. Для сети 230 В надо работать
с пиком 325В, а не только 230В. Соотношение делителей 1:40 кажется лучшим. Это позволяет работать с пиковым напряжением до 400 В.
Напряжение шунта ниже, чем напряжение делителя напряжения, поэтому подключается ко входу Y, который имеет лучшую точность.
Простая схема ваттметра:
Рис. 1 представляет собой простейшую конструкцию измерителя мощности (ваттметра) с AD633 и одного диапазона.
Ток измеряется шунтом. Если нам требуется преобразование выходного сигнала 1 мВ / 1 Вт, значение шунта должно быть
0R4 (0,4 Ом). Максимальный среднеквадратичный ток через измеритель определяется максимально допустимой рассеиваемой мощностью шунта.
Для шунта 0,4 Ом 40 Вт максимальный непрерывный ток составляет 10 А. Максимальная измеренная мощность составляет 2300 Вт для идеальной резистивной нагрузки, для разных нагрузок она должна быть ниже.Еще одно ограничение — максимальное входное напряжение умножителя (10 В),
поэтому максимальный пиковый ток должен быть ниже 25 А.
Калибровка выполняется путем установки P1 в соответствии с известной нагрузкой. Сумма значений P1 и R1 будет около 390k, а коэффициент деления будет 1:40.
Если вы не можете установить правильное значение с помощью P1, измените значение R1. Входы умножителя защищены от перенапряжения стабилитронами 12 В.
Напряжение питания (+/- 15 В) получается с помощью емкостного капельницы и двух стабилитронов на 15 В.В сочетании с мультиметром с разрешением 0,1 мВ вы получите ваттметр с разрешением 0,1 Вт. Мы будем использовать
Диапазоны 200 мВ, 2 В и, возможно, 20 В, где мощность
отображается непосредственно в ваттах (1 мВ = 1 Вт) или киловаттах (1 В = 1 кВт).
Предупреждение! Вся цепь, включая выход для мультиметра (вольтметра), электрически подключена к сетевому напряжению, что смертельно опасно.С этим следует обращаться соответственно. Для снижения риска возгорания следует использовать предохранитель или автоматический выключатель. Вы все делаете на свой страх и риск. Я не несу ответственности за причиненный вам вред.
Рис.1 — Схема простого ваттметра
AD633JN в корпусе DIP8.
Первые эксперименты с ваттметром
Макет ваттметра в макете.
Ваттметр на печатной плате.
Видео — тестирование ваттметра
Добавлен: 7. 3. 2011
дом
Как фактор мощности влияет на показания ваттметра?
Этот вид ваттметра не работает напрямую от коэффициента мощности. Он усредняет мгновенное напряжение, умноженное на ток. Сила на игле пропорциональна напряжению, умноженному на ток, который представляет собой мгновенную мощность. Пружина заставляет иглу линейно отклоняться под действием приложенной силы.Инерция стрелки усредняет мгновенное произведение тока и напряжения, поэтому показывает среднюю реальную мощность.
Если напряжение и ток не совпадают по фазе друг с другом на 90 ° (коэффициент мощности = 0), то мощность будет положительной в течение половины цикла и отрицательной в течение половины цикла. Если измеритель предназначен для нормальных частот линии электропередачи, то механический механизм не будет реагировать на отдельные полупериоды 50 или 60 Гц, но покажет вам отфильтрованную мощность нижних частот со значительно большей постоянной времени, чем отдельные циклы мощности.При коэффициенте мощности 0 это среднее значение будет равно 0, а счетчик покажет 0.
Если вы измеряете отдельно среднеквадратичное значение напряжения и тока, а затем умножаете их, вы получаете значение ВА (величина мощности, включая действительную и мнимую части). Вы можете взять реальную мощность, показанную измерителем, и разделить ее на значение ВА, чтобы получить коэффициент мощности.
Итак, опять же, этот измеритель не имеет прямого отношения к коэффициенту мощности. Он измеряет реальную мощность, возвращаясь к основным принципам, и является ли сигналы напряжения и тока синусами или нет.
Кстати, электросчетчик в вашем доме работает по такому же основному принципу. Вместо того, чтобы отклонять иглу от пружины, сила между катушками напряжения и тока заставляет небольшой двигатель вращаться. Общее количество оборотов — это интеграл от мощности по времени, или от общей переданной энергии. Ряд шестеренок вращает различные маркированные циферблаты, чтобы этот интеграл можно было накапливать и отображать, чтобы счетчик мог считывать итоговую сумму каждый месяц. Более новые счетчики автоматически отправляют накопленные показания в энергокомпанию через различные средства связи.
Быстрый ответ: как работает ваттметр
Ваттметр выполняет сложную работу, измеряя мощность, протекающую через электрическую цепь. Он одновременно измеряет значения напряжения и тока и умножает их, чтобы получить мощность в ваттах. Три основных типа — электродинамический, электронный и цифровой.
Ваттметр измеряет реальную мощность?
Ваттметр измеряет активную мощность. В особом случае реактивная мощность может быть измерена в 3-фазной симметричной схеме с помощью одного ваттметра.
Может ли ваттметр измерять мощность постоянного тока?
Ваттметр, безусловно, можно использовать для измерения мощности в цепи постоянного тока при условии, что он рассчитан на ток и напряжение, а также на постоянный ток (многие ваттметры содержат трансформаторы или асинхронные двигатели и могут работать только с переменным током). Коэффициент мощности не является проблемой в цепях питания постоянного тока.
Какую мощность потребляет ваттметр?
Потребляемая мощность измеряется путем расчета ее во времени с использованием как минимум одного полного цикла.- Как изолировать вашу систему воздуховодов на чердаке, шаг за шагом. Это вольтметр и амперметр. В среднем он потребляет 30 Вт (расчет: 0,6 Вт / 0,02 ч = 30 Вт).
Как измеряется мощность в цепи постоянного тока?
Электрическая мощность определяется как выполненная электрическая работа или рассеянная электрическая энергия в единицу времени. Он измеряется в Джоулях в секунду, то есть в ваттах. В случае цепей постоянного тока электрическая мощность — это произведение напряжения на ток.
Почему мы используем ваттметр?
Ваттметр — это прибор для измерения активной электрической мощности (или средней скорости потока электрической энергии) в ваттах любой данной цепи.Электромагнитные ваттметры используются для измерения полезной частоты и мощности звуковой частоты; другие типы требуются для радиочастотных измерений.
Может ли коэффициент мощности быть больше 1?
Коэффициент мощности, равный 1, означает, что нагрузка является чисто резистивной, а мощность потребляется на 100%. Если имеется реактивная нагрузка (индуктивная или емкостная), коэффициент мощности меньше 1, что означает потери мощности. Вы не можете потреблять больше, чем генерируется, поэтому PF никогда не может быть больше 1.
Что вы подразумеваете под трехфазным ваттметром?
Определение: Трехфазный ваттметр используется для измерения мощности трехфазной цепи. В трехфазном ваттметре два отдельных ваттметра монтируются вместе в одном блоке. Их движущиеся катушки размещены на одном шпинделе. Единственный элемент представляет собой комбинацию катушки давления и катушки тока.
Почему ваттметр LPF используется в тесте без нагрузки?
Ваттметр LPF предназначен для измерения мощности в индуктивных цепях.Индуктивные цепи обладают свойством запаздывания по коэффициенту мощности, поэтому используются эти ваттметры. Таким образом, ваттметр LPF (Low Power Factor) используется в ИСПЫТАНИИ ОТКРЫТОЙ ЦЕПИ трансформатора. При испытании на короткое замыкание закорачивается вторичная обмотка трансформатора.
Коэффициент мощности равен RZ?
Совет: Коэффициент мощности — это соотношение активной и полной мощности. F. — коэффициент мощности, R — реактивное сопротивление, Z — полное сопротивление. ⇒Z = √R2 + (XC − XL), где R — реактивное сопротивление, Z — полное сопротивление, XC — емкостное реактивное сопротивление, а XL — индуктивное реактивное сопротивление.
Какова формула коэффициента мощности?
Находится умножением (kVA = V x A). Результат выражается в единицах кВА. PF выражает отношение истинной мощности, используемой в цепи, к полной мощности, подаваемой в цепь.
Какой коэффициент мощности указан в моем счете за электричество?
Коэффициент мощности показывает, сколько мощности фактически используется нагрузкой для выполнения полезной работы и сколько энергии она «тратит впустую». Как ни банально звучит его название, это один из основных факторов, вызывающих высокие счета за электроэнергию, сбои в подаче электроэнергии, а иногда и дисбаланс в электрических сетях.
Что такое метод одного ваттметра?
Метод одного ваттметра В сбалансированной 3-проводной 3-фазной цепи нагрузки мощность в каждой фазе одинакова, и, следовательно, общая мощность схемы может быть определена путем умножения мощности, измеренной в любой одной фазе.
Почему в ваттметре происходит короткое замыкание МК?
Первоначальный ответ: Почему мы закорачиваем клеммы M & C во время подключения ваттметра? Основная и общая клеммы закорочены, чтобы создать конфигурацию стороны «нагрузка на токовую катушку», или вы можете сказать, чтобы разместить потенциальную катушку перед токовой катушкой.
Какой тип ваттметра нельзя использовать как для переменного, так и для постоянного тока?
Ваттметр какого типа нельзя использовать одновременно для переменного и постоянного тока? Ваттметр индукционного типа используется только для измерения переменного тока, тогда как ваттметр динамометрического типа используется только для измерения постоянного тока. Прибор электростатического типа не относится к категории ваттметров и используется для измерения напряжения.
Какой тип ваттметра широко используется?
Электростатический ваттметр подходит для высоковольтных цепей с низким коэффициентом мощности, таких как измерение диэлектрических потерь в конденсаторах.Они используются при измерениях очень малой мощности. Ваттметры индукционного типа и ваттметры с поворотной катушкой и прямым считыванием очень часто используются для измерения мощности.
Какова формула трехфазного питания?
3-фазные расчеты Для 3-фазных систем мы используем следующее уравнение: кВт = (В × I × PF × 1,732) ÷ 1000. Опять же, принимая единицу коэффициента мощности и решая это уравнение для «I», вы получаете: I = 1000 кВт ÷ 1,732 В.
Что такое CC и ПК в ваттметре?
Ваттметр используется для измерения средней мощности в любой электрической сети.Ваттметр имеет катушку напряжения или потенциала (PC) и катушку тока (CC) с маркировкой полярности, как показано на рисунке. Если одна из катушек перевернута, измеритель выдаст отрицательное значение мощности.
Как 3-ваттметр измеряет мощность?
Определение: Метод 3 ваттметра используется для измерения мощности в 3 фазах с использованием 4-проводной системы, которая основана на теореме Блонделя. Теорема Блонделя утверждает, что мощность, подаваемая системой переменного тока с k-проводом, равна общему ваттметру, который требуется меньше, чем тот, который равен «K-1».
Что определяет, насколько переместится стрелка ваттметра?
Последовательные катушки измеряют ток, протекающий по цепи, параллельная катушка измеряет напряжение. Последовательный резистор ограничивает ток через подвижную катушку. Он расположен между двумя неподвижными катушками и прикреплен к стрелке индикатора. Магнитные поля во всех трех катушках влияют на движение стрелки.
Что такое постоянная ваттметра?
Ваттметр — это электрический прибор, который используется для измерения электрической мощности (в ваттах) любой электрической цепи.Конструкция: он состоит из двух катушек, т.е. катушки давления (параллельной) и катушки тока (последовательной).
Измерение трехфазной мощности: метод трех ваттметров
Измерение мощности в цепи переменного тока измеряется с помощью ваттметра. Ваттметр — это прибор, который состоит из двух катушек, называемых Токовая катушка и Потенциальная катушка.
Токовая катушка с низким сопротивлением подключена последовательно с нагрузкой, так что по ней проходит ток нагрузки.
Катушка потенциала, имеющая сопротивление, подключена к нагрузке и пропускает ток, пропорциональный разности потенциалов.
Для измерения мощности в трехфазной или многофазной системе требуется более одного ваттметра, или один ваттметр снимает более одного показания. Если для измерения подключено более одного ваттметра, процесс становится удобным и простым в работе вместо снятия различных показаний одним ваттметром.
Количество ваттметров, необходимых для измерения мощности в данной многофазной системе, определяется теоремой Блонделя.
Согласно теореме Блонделя — Когда питание подается по системе переменного тока с проводом K, количество ваттметров, необходимых для измерения мощности, на единицу меньше количества проводов, т. Е. (K-I), независимо от того, что нагрузка сбалансирована или несимметрична.
Следовательно, три ваттметра требуются для измерения мощности в трехфазной четырехпроводной системе, тогда как только два ваттметра требуются для измерения мощности в трехфазной трехпроводной системе. В этой статье обсуждается метод измерения мощности с использованием трех ваттметров.
Трехваттметровый метод измерения трехфазной мощности
Метод трех ваттметров используется для измерения мощности в трехфазной четырехпроводной системе. Однако этот метод также можно использовать в трехфазной трехпроводной нагрузке, подключенной по схеме «треугольник», где мощность, потребляемая каждой нагрузкой, должна определяться отдельно.
Подключение нагрузок, подключенных звездой, для измерения мощности методом трех ваттметров показано ниже:
Катушка давления всех трех ваттметров, а именно W 1 , W 2 и W 3 , подключена к общей клемме, известной как нейтральная точка .Произведение фазного тока и линейного напряжения представляет собой фазную мощность и регистрируется отдельным ваттметром.
Полная мощность в методе измерения мощности трех ваттметров определяется как алгебраическая сумма показаний трех ваттметров. т.е.
Где,
W 1 = V 1 I 1
Вт 2 = V 2 I 2
Вт 3 = V 3 I 3
За исключением трехфазной, четырехпроводной несимметричной нагрузки, трехфазную мощность можно измерить только с помощью метода двух ваттметров.
См. Также: Метод измерения мощности с помощью двух ваттметров
Измерение трехфазной мощности
В этой статье объясняется измерение трехфазной мощности в нагрузке, соединенной звездой или треугольником, с использованием методов ваттметра.
Мощность в трехфазной нагрузке можно измерить следующими методами:
- Метод трех ваттметров
- Метод двух ваттметров
- Метод одного ваттметра
Название этих методов указывает количество ваттметров, используемых при измерении трехфазной мощности.
Что такое ваттметр?
Ваттметр — это оборудование, используемое для измерения мощности в цепи. Он состоит из двух типов катушек. Их:
- Токовая катушка с низким сопротивлением .
- Катушка давления или потенциала , обладающая высоким сопротивлением .
Катушка тока подключена последовательно с линией, по которой проходит ток. Катушка давления подключена к двум точкам, разность потенциалов которых должна быть измерена.См. Рисунок для подключения ваттметра.
Подключение ваттметраВаттметр показывает показание, пропорциональное произведению трех значений. Их
- Ток (I) через его токовую катушку.
- Разность потенциалов (В) на его катушке давления.
- Косинус угла между напряжением и током (Cosϕ).
P = VICos (ϕ)
Сравнение методов измерения мощности в трехфазной цепи показано в таблице ниже.
| Метод трех ваттметров | Используется для измерения 3-х фазных 4-х проводных цепей. Как сбалансированные, так и несбалансированные нагрузки. |
| Метод одного ваттметра | Используется в сбалансированной 3-фазной 3-проводной цепи нагрузки. |
| Метод двух ваттметров | Используется как в симметричных, так и в несимметричных 3-фазных, 3-проводных цепях |
Метод трех ваттметров
Теперь мы объясним измерение трехфазной мощности методом трех ваттметров.
Метод трех ваттметров используется для измерения мощности в 3-фазных, 4-проводных цепях. Однако этот метод также можно использовать в трехфазной нагрузке с трехпроводным подключением по схеме «треугольник», где мощность, потребляемая каждой нагрузкой, должна определяться отдельно.
На рисунке ниже показано подключение трех ваттметров к трехфазной четырехпроводной нагрузке, подключенной звездой.
Метод трех ваттметровКак показано на рисунке, три ваттметра подключены в каждой из трех фаз для измерения трехфазного энергопотребления нагрузки, независимо от того, подключены они по схеме звезды или треугольника.
Катушка тока каждого ваттметра пропускает ток только одной фазы, а катушка давления измеряет фазное напряжение фазы. Следовательно, каждый ваттметр измеряет мощность в одной фазе. Полная мощность нагрузки определяется алгебраической суммой показаний трех ваттметров.
P = W1 + W2 + W3
где, W1 = V1 * I1, W2 = V2 * I2, W3 = V3 * I3
Недостатки метода трех ваттметров
При использовании метода трех ваттметров возникает следующая трудность:
- В случае 3-фазной, 3-проводной нагрузки, подключенной звездой, трудно получить нейтральную точку, которая требуется для подключения.В особых случаях, когда необходимо использовать этот метод, можно сформировать «искусственную звезду».
- В случае цепей, соединенных треугольником, сложность использования этого метода связана с тем, что фазовые катушки необходимо разрывать для вставки катушек тока ваттметров.
Для измерения мощности необязательно использовать три ваттметра, для этого можно использовать даже два ваттметра.
За исключением трехфазной, четырехпроводной несимметричной нагрузки, трехфазная мощность измеряется только методом двух ваттметров.
Метод одного ваттметра
Следующий метод, который мы собираемся обсудить, — это метод одного ваттметра.
В этом методе измерения трехфазной мощности катушка тока подключается к любой одной линии, а катушка давления поочередно подключается между этой и двумя другими линиями. Схема подключения представлена на рисунке ниже.
Метод одного ваттметраТаким образом, мы получим два показания для сбалансированной нагрузки. Полученные таким образом два показания соответствуют показаниям, полученным обычным методом двух ваттметров.
Сбалансированная нагрузка — это нагрузка, которая потребляет одинаковый ток из каждой фазы трехфазной системы, в то время как несимметричная нагрузка имеет по крайней мере один из этих токов, отличный от остальных.
В симметричной 3-проводной 3-фазной цепи нагрузки мощность в каждой фазе одинакова. Следовательно, общую мощность схемы можно определить, умножив мощность, измеренную в любой одной фазе, на три.
Общая мощность при сбалансированной нагрузке = 3 x мощность на фазу
= 3 x показание ваттметра
Недостатки метода одного ваттметра
Этот метод не имеет такого универсального применения, как метод двух ваттметров, поскольку он ограничен только справедливой балансировкой нагрузок.Даже небольшая несбалансированность нагрузки приводит к большой погрешности измерения.
Однако его можно удобно применить, например, когда требуется найти мощность, потребляемую заводским двигателем, чтобы проверить нагрузку на двигатель.
Метод двух ваттметров
Как видно из названия, в этом методе для измерения трехфазной мощности используются два ваттметра. Это самый популярный метод из трех.
Этот метод обычно используется для измерения мощности в 3-фазных, 3-проводных цепях нагрузки.Его можно использовать для измерения мощности нагрузки, подключенной по схеме звезда / треугольник, в сбалансированном или несимметричном состоянии.
Помните, что сбалансированная нагрузка — это нагрузка, которая потребляет одинаковый ток из каждой фазы трехфазной системы, в то время как несимметричная нагрузка имеет по крайней мере один из этих токов, отличный от остальных.
В методе двух ваттметров катушки тока двух ваттметров вставляются в любые две линии, а катушки давления каждого ваттметра присоединяются к третьей линии. См. Рисунок ниже для лучшего понимания.
Метод двух ваттметровНа рисунке выше показано соединение двух ваттметров нагрузки, подключенной звездой. Аналогичным образом используются нагрузки, подключенные по схеме треугольник. Метод двух ваттметров может использоваться независимо от сбалансированной или несбалансированной нагрузки.
Алгебраическая сумма двух показаний ваттметра дает общую мощность в трехфазных, трехпроводных цепях нагрузки, соединенных звездой или треугольником, независимо от того, сбалансирована ли нагрузка или нет.
P = W1 + W2
Как работает ваттметр? — Wira Electrical
На этот раз мы попытаемся понять принцип работы ваттметра.
Некоторые ваттметры не имеют катушек; рассматриваемый здесь ваттметр относится к электромагнитному типу.
Обязательно сначала прочтите, что такое цепь переменного тока.
Измерение мощности ваттметром
Средняя мощность, потребляемая нагрузкой, измеряется прибором, называемым ваттметром .
Ваттметр — это прибор, используемый для измерения средней мощности.
На рисунке (1) показан ваттметр, который состоит по существу из двух катушек: токовой катушки и катушки напряжения.
Токовая катушка с очень низким импедансом (в идеале бесконечным) подключается параллельно нагрузке, как показано на рисунке (2), и реагирует на напряжение нагрузки.
| Рис. 1. Ваттметр |
Катушка тока действует как короткое замыкание из-за ее низкого импеданса; катушка напряжения ведет себя как разомкнутая цепь из-за своего высокого импеданса.
В результате наличие ваттметра не нарушает цепь и не влияет на измерение мощности.
| Рисунок 2. Ваттметр, подключенный к нагрузке |
Когда две катушки находятся под напряжением, механическая инерция подвижной системы создает угол отклонения, который пропорционален среднему значению продукт v (t) i (t) .
Если ток и напряжение нагрузки равны v (t) = V m cos (ωt + θ v ) и i (t) = I m cos (ωt + θ i ), их соответствующие среднеквадратичные векторы равны
, а ваттметр измеряет среднюю мощность, определяемую как
, как показано на рисунке.(2) каждая катушка ваттметра имеет две клеммы с маркировкой ±.
Чтобы обеспечить отклонение по шкале, клемма ± токовой катушки направлена к источнику, а клемма ± катушки напряжения подключена к той же линии, что и токовая катушка.

