Калькулятор расчета индуктивности катушки без сердечника. Расчет индуктивности катушки без сердечника: формулы, методы и практические советы

Как рассчитать индуктивность катушки без сердечника. Какие факторы влияют на индуктивность. Какие формулы используются для расчета. Как правильно намотать катушку для получения нужной индуктивности. Какие есть особенности расчета для разных типов катушек.

Что такое индуктивность катушки и от чего она зависит

Индуктивность катушки — это способность катушки накапливать энергию магнитного поля при протекании через нее электрического тока. Индуктивность измеряется в генри (Гн) и обозначается буквой L.

Основные факторы, влияющие на индуктивность катушки без сердечника:

• Геометрические размеры катушки (диаметр, длина)
• Число витков
• Способ намотки (плотность намотки)
• Форма сечения провода

Чем больше диаметр и длина катушки, тем выше ее индуктивность. Также индуктивность прямо пропорциональна квадрату числа витков. Плотная намотка виток к витку дает большую индуктивность по сравнению с намоткой с промежутками между витками.

Формулы для расчета индуктивности однослойных цилиндрических катушек

Для расчета индуктивности однослойных цилиндрических катушек без сердечника чаще всего используются следующие формулы:

Формула Уиллера:

L = (D^2 * N^2) / (18D + 40l)

где:

• L — индуктивность, мкГн
• D — диаметр катушки, см
• N — число витков
• l — длина намотки, см

Формула Нагаока:

L = 0.001 * π * N^2 * D * K / l

где K — поправочный коэффициент Нагаока, зависящий от отношения длины катушки к ее диаметру.

Пошаговый алгоритм расчета индуктивности катушки

Чтобы рассчитать индуктивность катушки, выполните следующие шаги:

1. Определите геометрические размеры катушки — диаметр и длину намотки
2. Задайтесь числом витков
3. Выберите подходящую формулу расчета
4. Подставьте значения в формулу и вычислите индуктивность
5. При необходимости скорректируйте число витков и повторите расчет

Если требуется намотать катушку с заданной индуктивностью, действуйте в обратном порядке — задайтесь индуктивностью и рассчитайте необходимое число витков.

Особенности расчета многослойных катушек

Для многослойных катушек без сердечника расчет индуктивности усложняется. В этом случае используют более сложные формулы, учитывающие:

• Число слоев намотки
• Толщину изоляции между слоями
• Взаимную индуктивность между слоями

Одна из формул для приближенного расчета индуктивности многослойной катушки:

L = 0.315 * (D * N)^2 / (6D + 9l + 10h)

где h — толщина обмотки (разница между внешним и внутренним диаметрами).

Практические рекомендации по намотке катушек индуктивности

При самостоятельном изготовлении катушек индуктивности следуйте этим советам:

• Используйте каркас из диэлектрического материала (пластик, керамика)
• Для плотной намотки применяйте провод с качественной изоляцией
• Закрепляйте концы обмотки для предотвращения разматывания
• При многослойной намотке прокладывайте слои изоляционным материалом
• Покройте готовую катушку лаком для защиты от влаги

Правильная намотка позволит получить катушку с параметрами, близкими к расчетным.

Влияние частоты на индуктивность катушки

Индуктивность катушки без сердечника практически не зависит от частоты в широком диапазоне. Однако на высоких частотах начинают проявляться паразитные эффекты:

• Скин-эффект в проводе обмотки
• Собственная емкость между витками
• Потери в диэлектрике каркаса

Эти факторы приводят к снижению действующей индуктивности катушки на высоких частотах. Для ВЧ и СВЧ катушек требуется учитывать эти эффекты при расчете.

Программы для автоматизированного расчета катушек индуктивности

Для упрощения расчетов катушек индуктивности можно использовать специализированные программы:

• Coil32 — бесплатная программа для Windows с широкими возможностями
• Mini Ring Core Calculator — онлайн-калькулятор для расчета катушек на ферритовых кольцах
• Coil Winding Calculator — мобильное приложение для Android

Такие программы позволяют быстро рассчитать параметры катушек различных конструкций и подобрать оптимальные размеры для заданной индуктивности.

Измерение индуктивности готовой катушки

После изготовления катушки рекомендуется проверить ее реальную индуктивность. Для этого используются:

• LC-метры
• Измерители RLC
• Анализаторы импеданса

Измерение позволяет убедиться в правильности расчетов и намотки. При значительном отклонении от расчетного значения может потребоваться корректировка числа витков.

Заключение

Расчет индуктивности катушки без сердечника — важный этап при проектировании различных радиотехнических устройств. Правильный выбор конструкции и точный расчет позволяют получить катушку с требуемыми параметрами. Использование современных методов расчета и измерений обеспечивает высокую точность изготовления катушек индуктивности.

РАДИОТЕХНИЧЕСКИЕ РАСЧЕТЫ

силовой трансформатор   радиотехнические расчеты   радио калькулятор

                РАДИОТЕХНИЧЕСКИЕ РАСЧЕТЫ

Во время конструирования радиолюбителю приходится производить массу расчетов. Один из самых трудоемких - расчет колебательного контура. Рассмотрим методику такого расчета. 

Как и при любом расчете нам нужны будут исходные данные. Предположим, нам нужно рассчитать частоту колебательного контура для фиксированных значений емкости конденсатора и индуктивности катушки. Допустим, емкость конденсатора равна 10 пикофарадам, индуктивность катушки — 10 микрогенри. По формуле (1 (А)) определяем частоту. Она равна 15900 килогерц (то есть 15,9 Мегагерца). При расчете индуктивности катушки при известных частоте настройки  и емкости контура используем формулу 1(В).

Для расчета емкости конденсатора используется формула 1(С).

Статья из журнала «Радио» для упрощенного расчета колебательного контура лежит здесь. Номограмму по расчету числа витков и размера катушек можно скачать по этой ссылке.  Обе статьи в формате DjVu — программу для их чтения можно скачать здесь.

Емкости конденсаторов и сопротивления резисторов имеют стандартный числовой ряд, но иногда требуются нестандартные значения. Как можно выйти из такого положения? Можно взять несколько, например, резисторов и соединить их так, чтобы получить нужное значение.

Пользуясь формулой (2) можно рассчитать величину, которую мы получим в результате параллельного (а), либо последовательного (b) соединения резисторов. При последовательном соединении резисторов их номиналы складываются между собой. Параллельное соединение позволяет получить результирующее сопротивление всегда меньшее, чем номинал наименьшего из соединяемых резисторов. При любом способе соединения резисторов (из рассмотренных) общая мощность рассеяния их увеличивается. Кроме того, при параллельном соединении через резисторы можно пропустить больший ток без их порчи.

Соединение конденсаторов:

При последовательном соединении конденсаторов (формула 3(b)) результирующая емкость будет всегда меньше емкости наименьшего из соединяемых конденсаторов. При параллельном соединении (3(a)) результирующая емкость будет равна сумме емкостей конденсаторов.

При работе на переменном токе иногда приходится рассчитывать реактивные сопротивления катушек индуктивности и конденсаторов.

Реактивное сопротивление катушки можно определить, пользуясь формулой (4), сопротивление конденсатора на переменном токе можно вычислить при помощи формулы (5):

 

В обоих формулах «Pi» — это всем известная математическая константа «Пи», равная (округленно) 3,14.

В заключении хотелось бы обратить ваше внимание на сноски в формулах. Для того, чтобы получить истинное значение при расчетах не забывайте использовать нужные величины!

В дальнейшем мы с вами рассмотрим формулы расчета катушек индуктивности с сердечником и без сердечника.

Расчет катушки индуктивности на стержневом сердечнике

Маркировка

Различное конструктивное исполнение геометрии проводника, использование разнообразных типов изоляции провода для обмоток трансформаторов, остальные электротехнические свойства в «ПУЭ» привели к созданию регламентированных аббревиатур их маркировки.

Первый буквенный символ в такой аббревиатуре обозначает сам материал проводника: «А» – дает понимание, что провод обмотки алюминиевый. Другой символ обозначает нихром, а его отсутствие принято считать, что проводник медного исполнения.

Второй поясняет о том, что это непосредственно сам провод для обмотки, а последующие дают обозначение к какому типу и материалу диэлектрика относится его изоляция.

В маркировке используются и цифровые символы, после буквенных. Ими принято обозначать сечение проводника, а также максимально допустимое напряжение изоляции, на который рассчитан провод. В других случаях цифры могут относится к количеству слоев изоляции. Примеры обмоточных проводов трансформаторов:

• ПЭМ-1 – медный провод с эмалированной изоляцией в один слой;
• ПКР-1 – медный провод с капроновой изоляцией в одну прядку.

Запомнить все маркировки проводников для обмоток практически невозможно. Главное знать принцип составления этих маркировок и обладать умением пользоваться справочной литературой для его верного подбора.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I — сила тока в катушке , А 

U — напряжение в катушке, В 

 R — сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.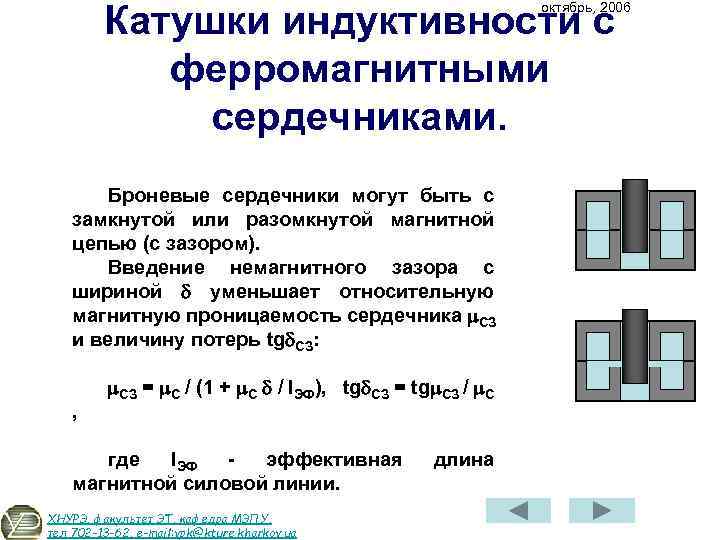

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Расчёт поправки на взаимную индуктивность витков

В общем случае поправка на взаимную индуктивность витков ∆₂L катушки определяется выражением

где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

J – коэффициент, зависящий формы катушки и от числа витков катушки.

1. Для катушки выполненной в один слой по длине катушки (соленоид):

а) при определении расчётной индуктивности L_P толщина намотки t принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит

где ω – количество витков катушки.

2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):

а) при определении расчётной индуктивности L_P длина катушки l принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит

где ω – количество витков катушки.

На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.

ДОМОСТРОЙСантехника и строительство

• Рубрика: Строительство
• Ссылка на пост
• https://firmmy.ru/

Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.

2018-04-07В электрической цепи, схема которой показана на рисунке, все резисторы одинаковые, и сопротивление каждого из них равно $R$.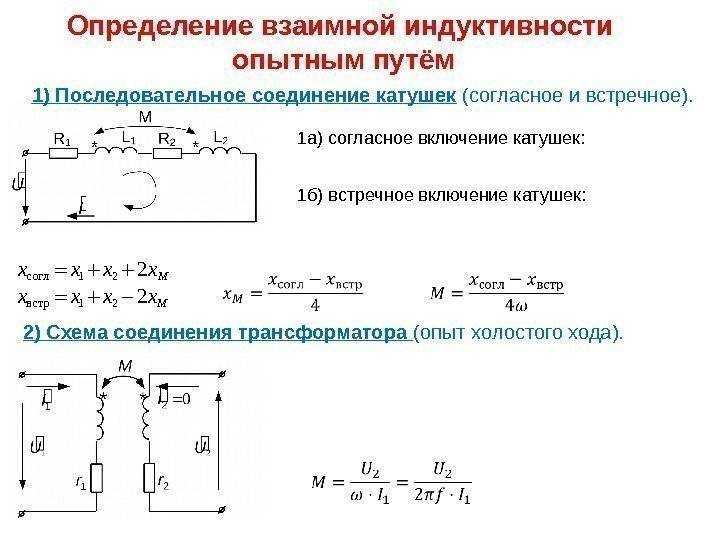 Цепь очень давно подключена к источнику переменного напряжения $U(t) = U_ cos omega t$. ?мкость $C$ конденсатора и индуктивность $L$ катушки подобраны таким образом, что выполняется соотношение: $omega L = 1/( omega C)$. 1) Найдите максимальное напряжение на конденсаторе. 2) Найдите максимальную силу тока, протекающего через катушку. 3) Ключ К замыкают в момент, когда ток через катушку не течёт. Найдите количество теплоты, которое выделится в каждом из резисторов, расположенных на рисунке справа от ключа К, после его замыкания. 4) Как изменятся ответы для количеств теплоты, выделившихся в тех же резисторах, если ключ размыкают в момент, когда ток через катушку максимален? 5) Как изменятся ответы на вопросы 1), 2), 3) и 4), если катушка и конденсатор будут подключены к тем же точкам А и В не параллельно друг другу, а последовательно друг за другом?

Поскольку в условии сказано, что цепь была подключена к источнику переменного напряжения давно, то это означает, что все переходные процессы в такой цепи давно прекратились. )$.

• 10 — 11 классы
• Физика
• 8 баллов

К конденсатору, заряд которого 250 пКл, подключили катушку индуктивности. Определите максимальную силу тока (в мА), протекающего через катушку, если циклическая частота свободных колебаний в контуре 8·107 рад/с.

Источник

Какие параметры есть у катушки

От того, где будет применяться индуктивный элемент и на какой частоте работать, зависит его исполнение. Имеются общие параметры:

• L – индуктивность;
• R пот – сопротивление потерь;
• Q – добротность;
• свой резонанс и паразитарная ёмкость;
• коэффициенты ТКИ и ТКД.

Индуктивность (коэффициент самоиндукции) L – это главная электрическая характеристика элемента, которая показывает количество накапливаемой дросселем энергии при передвижении тока. Величина энергии в катушки тем выше, чем больше её индуктивность. Единица измерений L – 1 Гн.

При взаимодействии тока и магнитного поля в обмотке возникают вредные явления.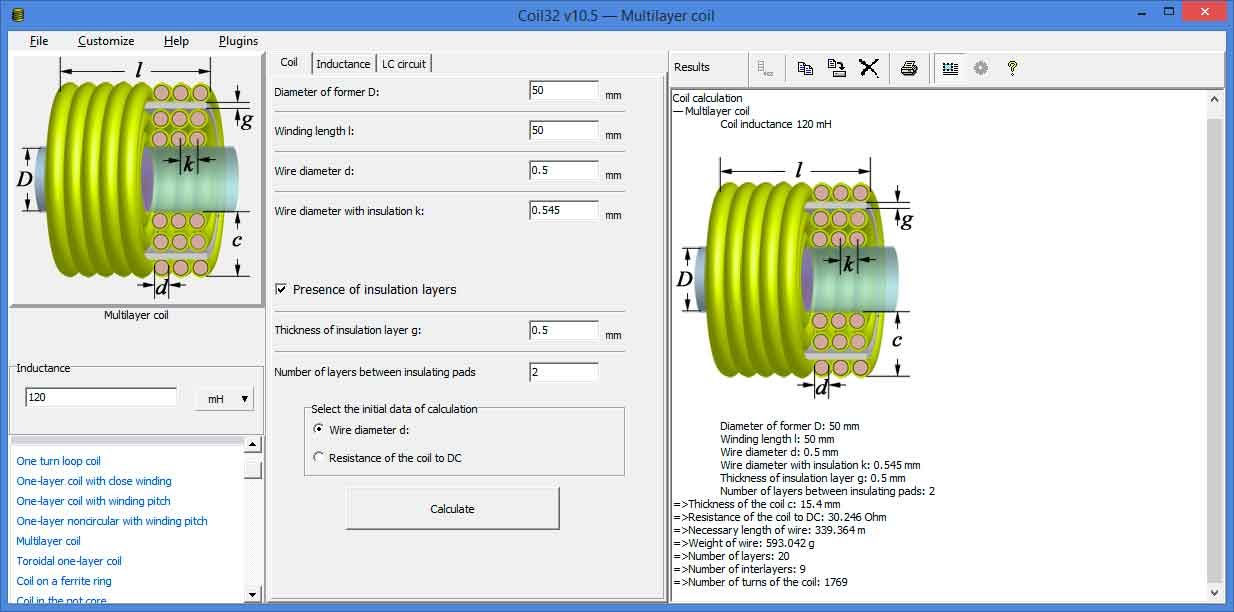 Они способствуют возникновению потерь, которые обозначают R пот. Формула потерь имеет вид:

R пот = rω + rd + rs + re.

Слагаемые формулы – это потери:

• rω – в проводах;
• rd – в диэлектрике;
• rs – в сердечнике;
• re – на вихревые токи.

В результате таких потерь импеданс индуктивного двухполюсника нельзя назвать целиком реактивным.

Добротность двухполюсника определяется по формуле:

Q = ω*L/R пот,

где ω*L = 2π*L – реактивное сопротивление.

При наматывании витков элемента между ними возникает ненужная ёмкость. Из-за этого дроссель превращается в колебательный контур с собственным резонансом.

ТКИ – показатель, описывающий зависимость L от Т0С.

ТКД – показатель, описывающий зависимость добротности от Т0С.

Информация. Изменение основных параметров индуктивного двухполюсника зависит от коэффициентов ТКИ, ТКД, а также от времени и влажности.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I – сила тока в катушке , А 

U – напряжение в катушке, В 

 R – сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.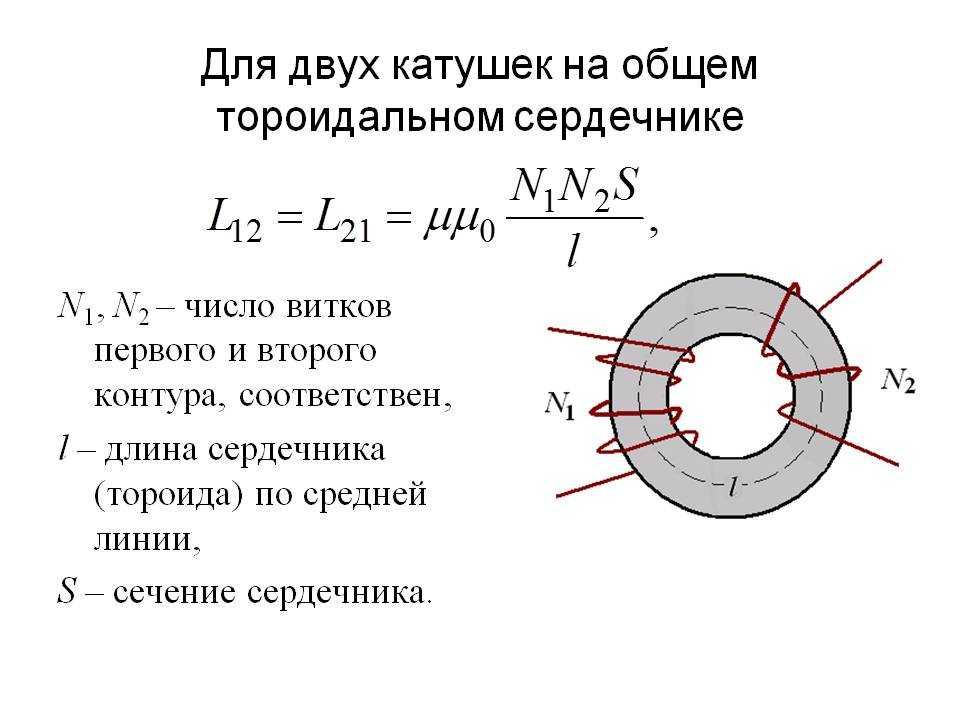

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Расчет катушки индуктивности | Postroydo

Вы хотите уникальный дизайн, полностью соответствующий вашим желаниям, отражающий вашу индивидуальность? Посмотрите на интерьеры из нашей галереи, возможно, что-то из них, будет полностью соответствовать вашим требованиям.

Отделка требует не только профессионалов, но и особенных материалов? У нас есть все, от болтика до плинтусов, от инструментов до мебельного гарнитура, от строительного шлака и песка до интерьерно-декоративных безделушек. И это еще не все! Если вам мало просто найти и купить стройматериалы или бытовую технику, но нужен еще тот кто, установит ее или выполнит необходимую работу, вы тоже можете сделать это здесь, на нашем сайте, буквально за две минуты.

Не имеет значения, нужно ли вам построить дом, дачу, баню или подобрать шторы в спальню – найти все необходимое, причем, не выходя из дома, можно на Postroydo.ru.

Если строительство, отделка или ремонт – ваше призвание, у нас для вас отличная новость: у нас ваши способности и знания оценят по достоинству. Так как основная аудитория Postroydo.ru – сотни тысяч человек, которые планируют строительство или ремонт, а это значит что среди них обязательно отыщется тот, кому ваши товары или услуги буквально жизненно необходимы. Так же у нас вы сможете встретить коллег и обсудить с ними насущные вопросы, поделиться опытом и мастерством или завязать прочные партнерские отношения.

Специально для вашего удобства и скорости работы мы расположили материалы таким образом, что их поиск не составляет труда и интуитивно понятен. К примеру здесь, мы собрали огромную и, поистине, уникальную по разнообразию галерею выполненных работ, включающая всевозможные интерьеры, экстерьеры домов, квартир и участков. Решения ландшафтного дизайна были разработаны ведущими отечественными и зарубежными специалистами.

Сайт Postroydo.ru создан в помощь всем тем, кто занялся стройкой или ремонтом, а также другим заинтересованным лицам. С нашей помощью вы можете взять или сдать в аренду спецтехнику, найти бригаду профессиональных каменщиков или штукатуров, подать или узнать о строительных тендерах и конкурсах.

Специально для вас мы собрали интереснейшие проекты, новости наших партнеров, ведущих компаний строительной индустрии, полезные рекомендации по выбору того или иного материала или технологий. В нашем каталоге вы с можно найти абсолютно все, что нужно мастерам и их заказчикам. Если вы так и не нашли то что искали, не беда, всегда можно объявить тендер на строительство или ремонт – вы будете  удивлены, как быстро найдется тот кто максимально точно решит и устранит вашу  проблему, ведь информация о вашей заявке получат тысячи компаний и частных мастеров! 

На нашем форуме вы можете задать вопрос и получить ответ опытного специалиста, поделиться своим опытом или рассказать о собственных достижениях. Ежедневно  мы регистрируем сотни строительных компаний и частных мастеров предоставляющих строительные, отделочные или ремонтные услуги.

Мы рады, что вы обратились к нам. Приятного просмотра!

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах.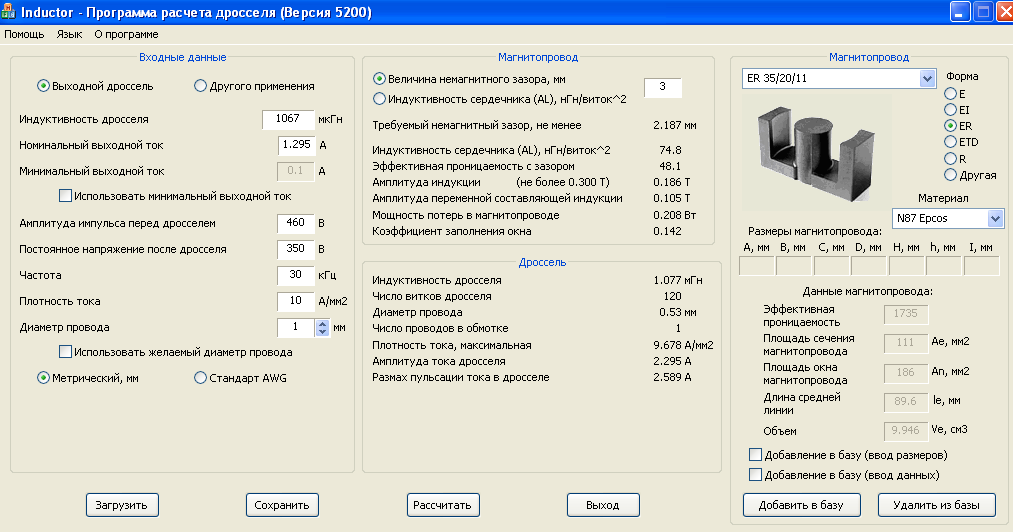 Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Катушка индуктивности в цепи переменного тока.

Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:

Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:

Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:

\varepsilon_L = -L\medspace\frac{dI}{dt}

Собственно, график нам и демонстрирует эту зависимость! Смотрите сами — между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.

Аналогично между точками 2 и 3 — ток уменьшается — скорость изменения тока отрицательная и увеличивается — ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика — там все процессы протекают по такому же принципу.

Кроме того, на графике можно заметить очень важный момент — при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены «навстречу» току источника).

А на участках 2-3 и 4-5 все наоборот — ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).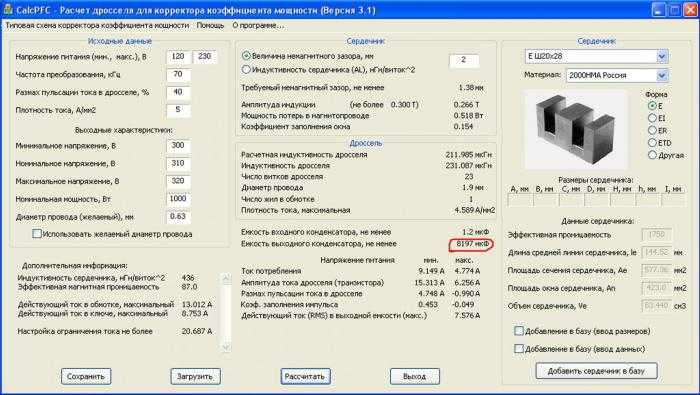

И в итоге мы приходим к очень интересному факту — катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:

X_L = w\medspace L

Где w — угловая частота: w = 2 \pi f. f — это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.

Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто, по 2-му закону Кирхгофа:

u + \varepsilon_L = 0

А следовательно:

u = - \varepsilon_L

Построим на одном графике зависимости тока и напряжения в цепи от времени:

Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:

Вот и с включением катушки в цепь переменного тока мы разобрались

На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

где ω – количество витков катушки,

R_M – сопротивление магнитной цепи,

μ_а – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

S_M – площадь поперечного сечения сердечника,

l_M – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность.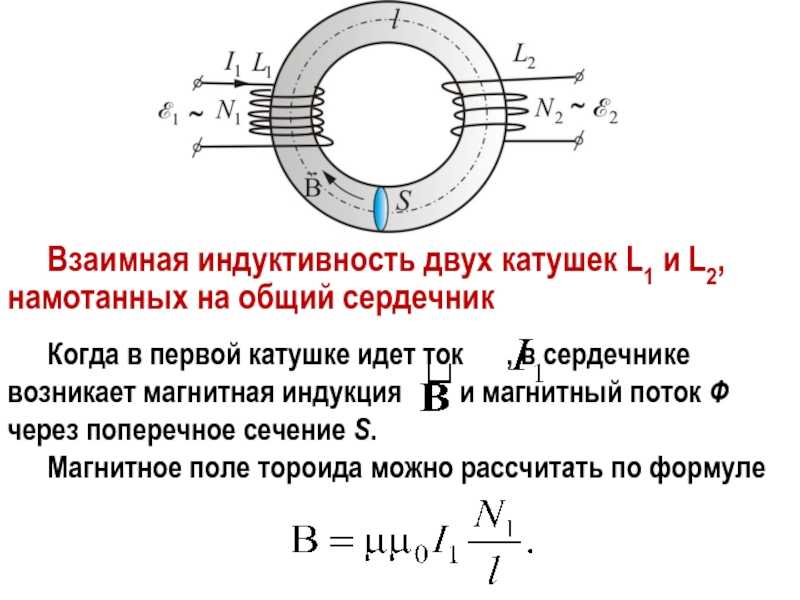 Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии l_e и эффективная площадь поперечного сечения S_e сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

где ω – количество витков катушки,

μ – магнитная постоянная, μ = 4π*10-7,

μ_r – относительная магнитная проницаемость вещества,

S_e – эффективная площадь поперечного сечения сердечника,

l_e – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;

С₂ – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;

где N – количество разнородных участков сердечника,

l_N – длина N – го участка сердечника,

S_N – площадь N – го участка сердечника.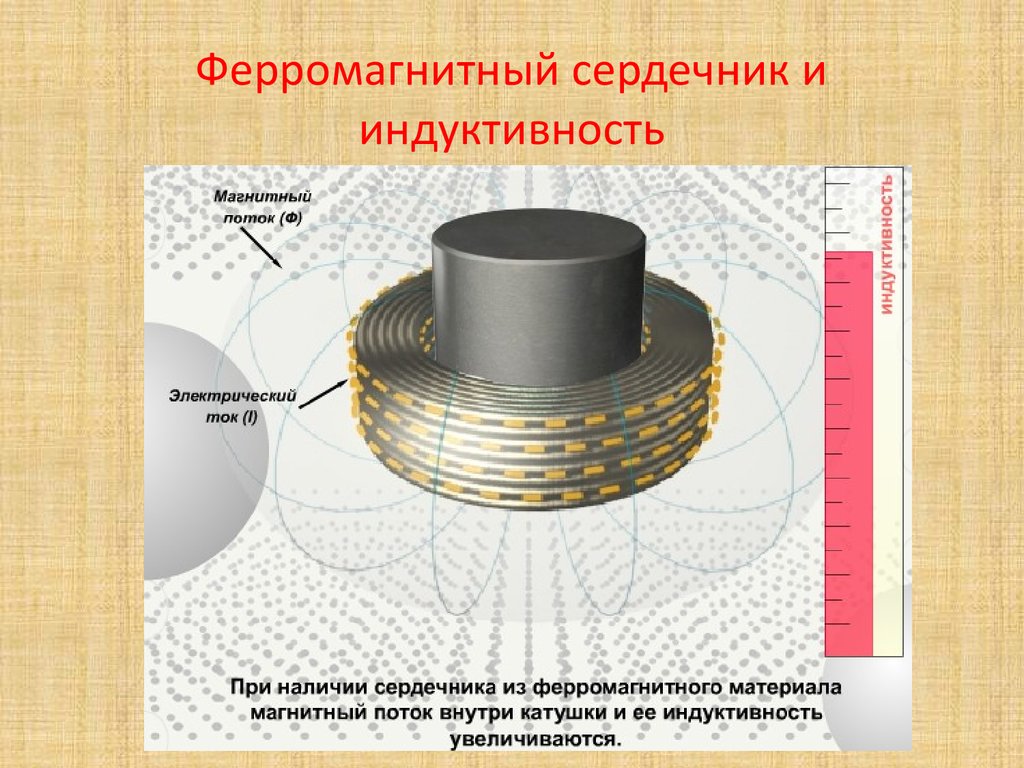

Тогда величины S_e и l_e определятся из следующих выражений

Кроме индуктивности с помощью постоянных С₁ и С­₂ определяют эффективный объём V_e, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С₁ по следующему выражению

где ω – количество витков катушки,

μ – магнитная постоянная, μ = 4π*10-7,

μ_r – относительная магнитная проницаемость вещества,

С₁ – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

Как произвести расчёт катушек индуктивности (однослойных, цилиндрических без сердечника)

Из книги «300 советов»

Индуктивность катушки зависит от её геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше её индуктивность.

Если катушка наматывается плотно виток к витку, то индуктивность её будет больше по сравнению с катушкой, намотанной неплотно, с промежутками между витками. Когда требуется намотать катушку по заданным размерам и нет провода нужного диаметра, то при намотке её более толстым проводом надо несколько увеличить, а тонким — уменьшить число витков катушки, чтобы получить необходимую индуктивность.

Все приведенные выше соображения справедливы при намотке катушек без ферритовых сердечников.

Расчёт однослойных цилиндрических катушек производится по формуле

L

= (D/10)2*n2/(4.5*D+10*l)

где L

— индуктивность катушки, мкГн;D — диаметр катушки, мм;l — длина намотки катушки, мм;n — число витков катушки. При расчёте катушки могут встретиться два случая:

а) по заданным геометрическим размерам необходимо определить индуктивность катушки;

б) при известной индуктивности определить число витков и диаметр провода катушки.

В первом случае все исходные данные, входящие в формулу, известны, и расчёт не представляет затруднений.

Пример. Определим индуктивность катушки, изображенной на рисунке; для этого подставим в формулу все необходимые величины:

L

= (18/10)2*202/(4.5*18+10*20) = 4.6 мкГн

Во втором случае известны диаметр катушки и длина намотки, которая, в свою очередь, зависит от числа витков и диаметра провода. Поэтому расчет рекомендуется вести в следующей последовательности. Исходя из конструктивных соображений определяют размеры катушки, диаметр и длину намотки, а затем рассчитывают число витков по формуле

n

= 10*(5*L *(0.9*D +2*l))1/2/D После того как будет найдено число витков, определяют диаметр провода с изоляцией по формуле

d=l/n

где d

— диаметр провода, мм,l — длина обмотки, мм,n — число витков.

Пример. Нужно изготовить катушку диаметром 10 мм при длине намотки 20 мм, имеющую индуктивность 0,8 мкГн. Намотка рядовая виток к витку.

Подставив в последнюю формулу заданные величины, получим:

n

= 10*(5*0.8*(0.9*10+2*20))1/2/10

Диаметр провода

d

= 20/14=1.43 мм

Если эту катушку наматывать проводом меньшего диаметра, то нужно полученные расчетным путем 14 витков разместить по всей длине катушки (20 мм) с равными промежутками между витками, т. е. с шагом намотки. Индуктивность данной катушки будет на 1-2% меньше номинальной, что следует учитывать при изготовлении таких катушек. При намотке в случае необходимости более толстым проводом, чем 1,43 мм, следует сделать новый расчёт, увеличив диаметр или длину намотки катушки. Возможно, также придётся увеличить и то и другое одновременно, пока не будут получены необходимые габариты катушки, соответствующие заданной индуктивности.

Следует заметить, что по приведённым выше формулам рекомендуется рассчитывать такие катушки, у которых длина намотки l

равна или больше половины диаметра. Если же длина намотки меньше половины диаметраD /2, то более точные результаты можно получить по формулам

L

=(D /10)2*n 2/((4D +11l ))

и

n

= (10L *(4D +11l ))1/2/D

Что такое катушка индуктивности

Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.

Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!

Индукторы (катушки) | Hioki

Что такое катушки индуктивности или катушки?

Катушки могут быть без сердечника (с воздушным сердечником или сердечником из немагнитного металла) или могут иметь сердечник из магнитного металла (т. е. металла с высокой магнитной проницаемостью), такого как феррит. Катушки индуктивности с сердечниками проявляют зависимость от тока.

Пример настройки условий измерения

*В противном случае используются настройки по умолчанию.
*Вышеупомянутые настройки относятся к пример измерения. Поскольку оптимальные условия меняются в зависимости от цель измерения, конкретные настройки должны определяться оператор прибора.

Установка частоты измерения

Явление LC-резонанса с индуктивностью катушки (индуктора) и паразитной емкостью известно как собственный резонанс. Частота, при которой возникает собственный резонанс, называется собственной резонансной частотой. При оценке катушек обязательно измеряйте L и Q на частоте, которая значительно ниже собственной резонансной частоты.

Индуктивность катушки, возрастающая с увеличением частоты, может быть рассчитана по следующей формуле: Z=j2πfL. Для эффективного измерения индуктивности при изменении частоты установите диапазон измерения на AUTO. Для более точного измерения установите частоту таким образом, чтобы получить импеданс, который можно измерить с высокой точностью.

Установка уровня измерительного сигнала

Измеряемый ток можно рассчитать по напряжению на открытой клемме, выходному импедансу прибора и импедансу объекта измерения. Установите измерительное напряжение таким образом, чтобы не превышался номинальный ток.

При измерении катушки, которая демонстрирует зависимость от тока (т. е. катушки с магнитным сердечником), установите прибор на такой уровень сигнала, чтобы магнитный сердечник не насыщался. При измерении катушки, не проявляющей зависимости от тока, рекомендуется настроить прибор на уровень сигнала с наилучшей точностью. В серии IM35xx наилучшая точность достигается при настройке 1 В режима V. В приборах серии IM758x уровень измеряемого сигнала определяется для мощности при использовании оконечной нагрузки 50 Ом порта ИУ, и настройка с наилучшей точностью составляет +1 дБмВт.

При измерении катушки с сердечником или катушки с низким номинальным током удобен режим CC (постоянный ток) серии IM35xx. Измерительный ток контролируется программным обеспечением, поэтому он остается постоянным.

Используемые продукты

Массовое производство

Исследования и разработки

*Дополнительную информацию см. в каталоге продукции.

Выбор параметра, Ls или Lp

Вообще говоря, режим последовательной эквивалентной схемы используется при измерении элементов с низким импедансом (приблизительно 100 Ом или менее), а режим параллельной эквивалентной схемы используется при измерении элементов с высоким импедансом (приблизительно 10 Ом). кОм или выше). Если соответствующий режим эквивалентной схемы неясен, например, при измерении образца с импедансом приблизительно от 100 Ом до 10 кОм, обратитесь к производителю компонента.
Катушка индуктивности будет вести себя так, как если бы потери в меди обмотки Rs и потери в сердечнике Rp были соединены с идеальной катушкой индуктивности L.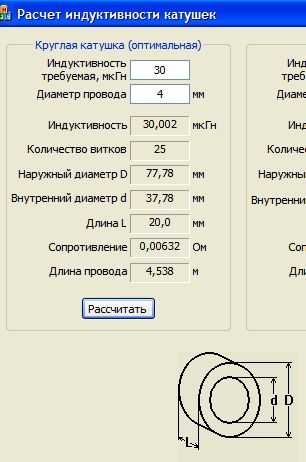 Индуктивность идеальной катушки можно рассчитать следующим образом: XL＝j2πfL. Хотя общая формулировка невозможна, поскольку она зависит от величины Rs и Rp, катушки с низкой индуктивностью характеризуются небольшим XL, что позволяет рассматривать импеданс при параллельном размещении Rp и L как примерно эквивалентный XL. Rs можно не учитывать, так как Ls мало, поэтому используется последовательная эквивалентная схема. Напротив, когда импеданс высок, Rp нельзя игнорировать, а Rs можно, поэтому схему можно рассматривать как параллельную эквивалентную схему.

Ток, протекающий по катушке

Ток, протекающий по катушке, можно рассчитать на основе напряжения разомкнутой клеммы, выходного импеданса прибора и импеданса объекта измерения.

*1 Выходное сопротивление различается в зависимости от модели и от того, включен ли высокоточный режим с низким сопротивлением. Пожалуйста, ознакомьтесь с техническими характеристиками продукта в инструкции по эксплуатации.

Измерение Rdc

При оценке катушки измеряются L, Q и Rdc. Такие приборы, как IM3533 и IM3536, могут измерять L, Q и Rdc без необходимости использования каких-либо других устройств. После измерения L и Q с сигналом переменного тока измерьте Rdc с сигналом постоянного тока.
*Rs и Rp не равны Rdc. Rs и Rp — значения сопротивления, которые измеряются сигналом переменного тока. Они включают такие компоненты, как потери в катушке и сопротивление обмотки, которое увеличивается из-за поверхностных эффектов проводника и эффектов близости.
Когда материал обмотки имеет большой температурный коэффициент, Rdc будет меняться в зависимости от температуры. IM3533 имеет функцию коррекции температуры для Rdc.

Характеристики суперпозиции постоянного тока

Характеристики катушки включают характеристики суперпозиции постоянного тока, которые указывают степень уменьшения индуктивности по отношению к постоянному току, что является важным параметром оценки для катушек, которые будут использоваться в цепях, таких как цепи питания, которые работают с большими токами .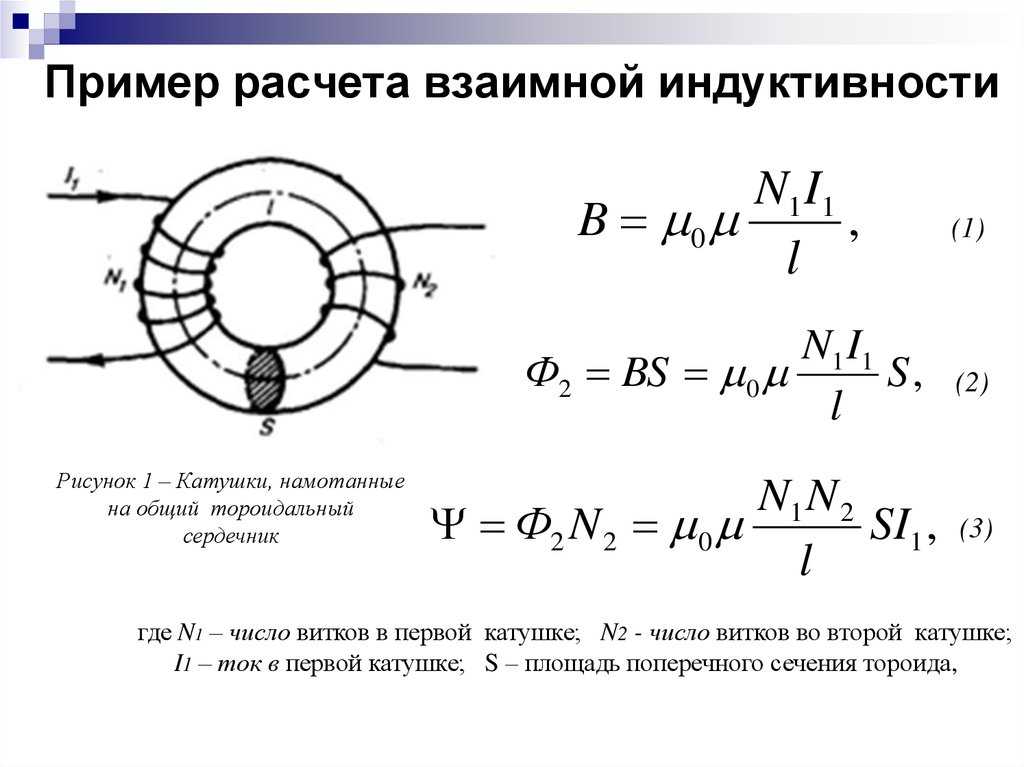
Функция приложения напряжения смещения постоянного тока, встроенная в счетчики Hioki LCR, предназначена для использования при измерении конденсаторов и не может использоваться для подачи постоянного тока. Чтобы наложить сигнал постоянного тока, используйте блок постоянного тока смещения 9269 (или 9269-10) и внешний источник питания или создайте для этой цели собственную схему.

Установка времени задержки

Чтобы уменьшить ошибку измерения при измерении постоянного тока, счетчики Hioki LCR циклически включают и выключают генерируемое напряжение для отмены внутреннего смещения (функция регулировки постоянного тока).
Когда напряжение, подаваемое на индуктор, изменяется, выходное сопротивление и эквивалентное последовательное сопротивление и индуктивность индуктора вызывают переходные процессы. Установите достаточно большое время задержки во время измерения Rdc, чтобы гарантировать, что эти явления не повлияют на результаты измерения. Название, присвоенное настройке времени задержки, зависит от модели, как и время измерения. Дополнительную информацию см. в руководстве по эксплуатации модели, которую вы собираетесь использовать.
Если вы не уверены в подходящем времени задержки, сначала установите максимально возможное время задержки. Затем постепенно сокращайте время задержки, проверяя, чтобы измеренные значения не отличались изменчивостью.

трансформатор — Индуктивность плоской (спиральной) катушки вблизи сплошной медной поверхности

Задать вопрос

спросил 4 года, 1 месяц назад

Изменено 4 года, 1 месяц назад

Просмотрено 156 раз

\$\начало группы\$

Я работаю над системой электромагнитной левитации, состоящей из плоского спирального (плоского) индуктора, расположенного над твердой медной поверхностью.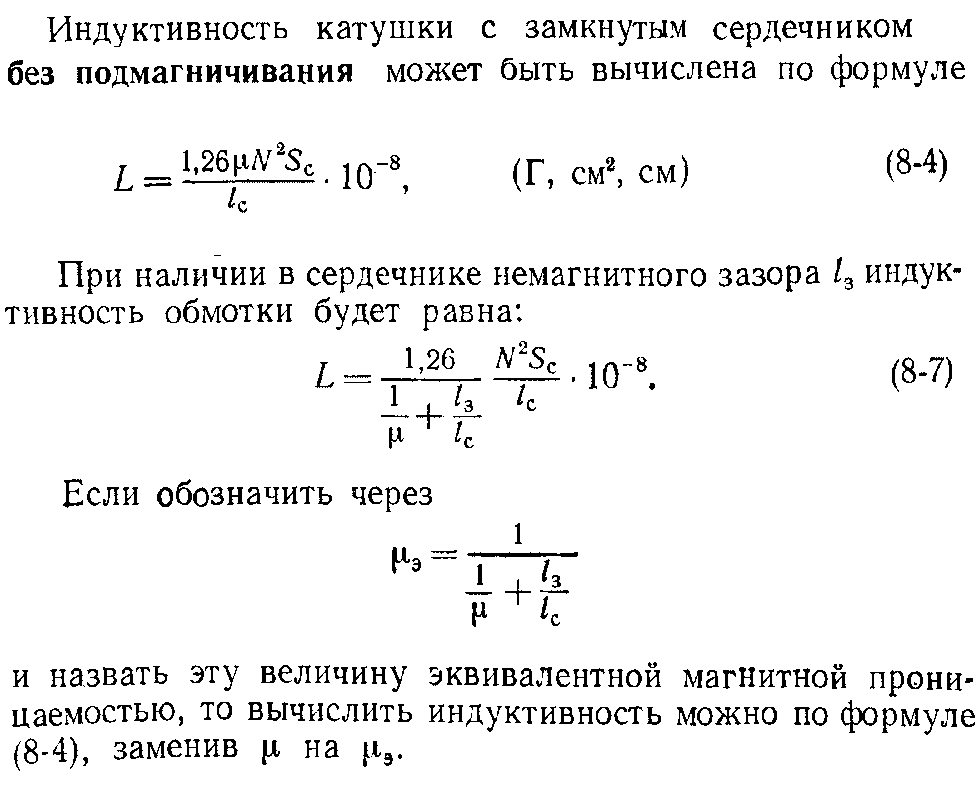 Плоская катушка параллельна поверхности меди. (Считайте, что и катушка, и поверхность состоят из 100% чистой меди, а поверхность бесконечна по площади и глубине.)

Я знаю, как рассчитать индуктивность спирального индуктора в свободном пространстве. На самом деле, в Интернете есть несколько калькуляторов, таких как этот.

Мой вопрос касается изменения индуктивности при приближении катушки к медной поверхности. Я думаю, что медную поверхность можно рассматривать как «закороченную вторичную обмотку» в трансформаторе без сердечника. Это означало бы, что индуктивность первичной обмотки на самом деле равна эффективной утечка индуктивность в зависимости от геометрии системы. Я полагаю, что если бы первичная обмотка (спиральная катушка) была поднесена бесконечно близко к вторичной обмотке (поверхность меди), индуктивность рассеяния была бы равна нулю. По мере удаления катушки от поверхности меди индуктивность рассеяния будет увеличиваться (вплоть до полной индуктивности катушки в свободном пространстве, на бесконечном расстоянии от поверхности меди внизу). Я думаю, что, вероятно, можно считать сопротивления незначительными (фактически равными нулю).

Я ищу две вещи:

1. Руководство по моему мышлению, подтверждение того, что я на правильном пути, или исправление, если нет.
2. Формула, которую я могу применить для расчета [изменения] индуктивности катушки при ее расположении на разных расстояниях от поверхности меди. (Обычные расстояния составляют порядка 1 мм для катушки диаметром 25 мм, FWIW.)

Я понимаю, что я действительно мог бы сконструировать эту систему в той или иной форме и измерить индуктивность и, возможно, даже эмпирически вывести формулу. Но я бы предпочел сначала смоделировать его, если это возможно.

• трансформатор
• электромагнетизм
• индуктивность
• физика
• взаимная индуктивность

\$\конечная группа\$

5

\$\начало группы\$

Вы правы в том, что индуктивность в идеале должна быть равна нулю на нулевом расстоянии.