Конденсатор c1. Особенности последовательного и параллельного соединения конденсаторов в электрических цепях

Как рассчитать общую емкость при последовательном и параллельном соединении конденсаторов. Какие преимущества дают разные типы соединений. Как правильно выбрать способ соединения конденсаторов для различных задач.

Основные принципы соединения конденсаторов

Конденсаторы в электрических схемах могут соединяться двумя основными способами — последовательно и параллельно. Каждый из этих способов имеет свои особенности и применяется для решения различных технических задач:

• При последовательном соединении конденсаторы включаются друг за другом в цепь. Это позволяет уменьшить общую емкость и увеличить допустимое рабочее напряжение.
• При параллельном соединении все конденсаторы подключаются к одним и тем же точкам цепи. Такое соединение увеличивает общую емкость.

Выбор способа соединения зависит от конкретных требований к электрической цепи. Рассмотрим подробнее особенности каждого типа соединения.

Расчет емкости при последовательном соединении конденсаторов

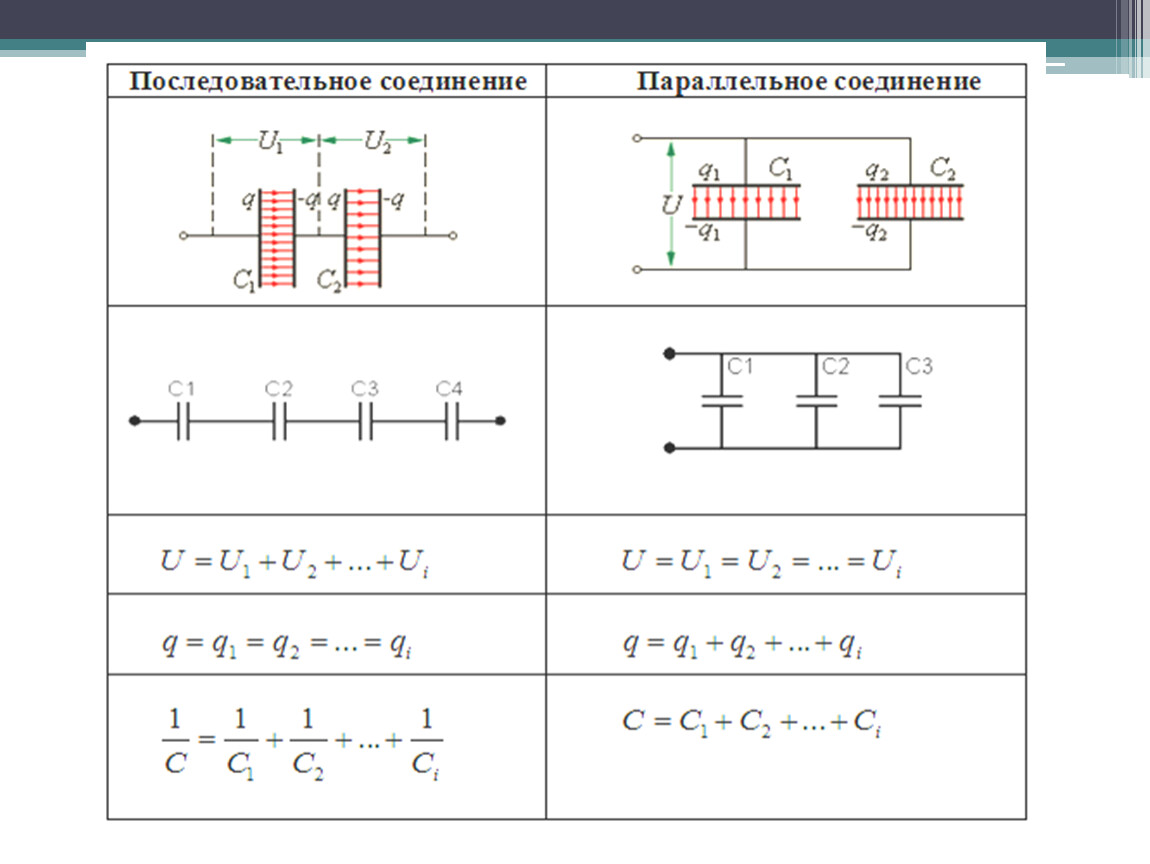
При последовательном соединении конденсаторов их общая емкость уменьшается. Это происходит потому, что увеличивается расстояние между обкладками эквивалентного конденсатора. Для расчета общей емкости используется следующая формула:

1/C = 1/C1 + 1/C2 + 1/C3 + …

Где C — общая емкость, C1, C2, C3 — емкости отдельных конденсаторов.

Как видно из формулы, обратная величина общей емкости равна сумме обратных величин емкостей отдельных конденсаторов. Это приводит к тому, что общая емкость всегда меньше емкости самого маленького конденсатора в цепи.

Особенности расчета емкости при параллельном соединении

При параллельном соединении конденсаторов их общая емкость увеличивается. Это происходит из-за увеличения площади обкладок эквивалентного конденсатора. Расчет общей емкости в этом случае производится по формуле:

C = C1 + C2 + C3 + …

Где C — общая емкость, C1, C2, C3 — емкости отдельных конденсаторов.

Таким образом, общая емкость при параллельном соединении равна сумме емкостей всех конденсаторов. Это позволяет получить большую емкость, используя несколько конденсаторов меньшей емкости.

Преимущества последовательного соединения конденсаторов

Последовательное соединение конденсаторов имеет ряд важных преимуществ:

• Увеличение максимального рабочего напряжения. При последовательном соединении напряжение распределяется между конденсаторами, что позволяет использовать цепь при более высоком напряжении.
• Уменьшение общей емкости. Это может быть полезно, когда требуется точная настройка емкости в цепи.
• Повышение надежности. При выходе из строя одного конденсатора цепь продолжает работать.

Однако стоит учитывать, что при последовательном соединении общая емкость всегда меньше емкости самого маленького конденсатора в цепи.

Когда применяется параллельное соединение конденсаторов

Параллельное соединение конденсаторов используется в следующих случаях:

• Когда необходимо увеличить общую емкость. Это часто требуется в фильтрах источников питания для сглаживания пульсаций.
• Для снижения эквивалентного последовательного сопротивления (ESR). Параллельное соединение уменьшает общее ESR, что улучшает характеристики цепи на высоких частотах.
• При необходимости использования нескольких конденсаторов меньшей емкости вместо одного большого. Это может быть обусловлено соображениями стоимости или доступности компонентов.

Параллельное соединение позволяет легко наращивать емкость путем добавления дополнительных конденсаторов.

Расчет напряжения на конденсаторах при последовательном соединении

При последовательном соединении конденсаторов важно учитывать, как распределяется напряжение между ними. Напряжение на каждом конденсаторе обратно пропорционально его емкости:

U1/U2 = C2/C1

Где U1, U2 — напряжения на конденсаторах, C1, C2 — их емкости.

Это означает, что на конденсаторе с меньшей емкостью будет большее напряжение. Поэтому при проектировании цепи необходимо убедиться, что напряжение на каждом конденсаторе не превышает его максимально допустимого значения.

Смешанное соединение конденсаторов

В реальных схемах часто встречается смешанное соединение, когда группы параллельно соединенных конденсаторов соединяются последовательно. Для расчета общей емкости в таком случае:

1. Сначала рассчитывают емкость каждой параллельной группы.
2. Затем полученные значения используют для расчета последовательного соединения.

Такой подход позволяет гибко настраивать характеристики цепи, комбинируя преимущества обоих типов соединения.

Практические рекомендации по соединению конденсаторов

При работе с конденсаторами в электрических схемах следует учитывать несколько важных моментов:

• Всегда проверяйте максимальное рабочее напряжение конденсаторов. При последовательном соединении оно должно быть выше, чем напряжение в цепи.
• Учитывайте допуски емкости конденсаторов. В реальных условиях емкость может отличаться от номинальной.
• При параллельном соединении используйте конденсаторы с близкими значениями ESR для оптимальной работы на высоких частотах.
• В цепях с высоким напряжением рекомендуется использовать выравнивающие резисторы при последовательном соединении конденсаторов.

Соблюдение этих рекомендаций поможет обеспечить надежную и эффективную работу электрической цепи.

Применение различных соединений конденсаторов в электронике

Разные способы соединения конденсаторов широко используются в различных областях электроники:

• В источниках питания параллельное соединение применяется для увеличения емкости фильтров, что улучшает сглаживание пульсаций.
• В высоковольтных цепях последовательное соединение позволяет использовать конденсаторы с меньшим рабочим напряжением.
• В радиотехнике смешанное соединение конденсаторов используется для создания сложных фильтров и цепей согласования.
• В импульсных преобразователях параллельное соединение конденсаторов помогает снизить ESR и улучшить характеристики на высоких частотах.

Правильный выбор способа соединения конденсаторов позволяет оптимизировать характеристики электронных устройств и повысить их эффективность.

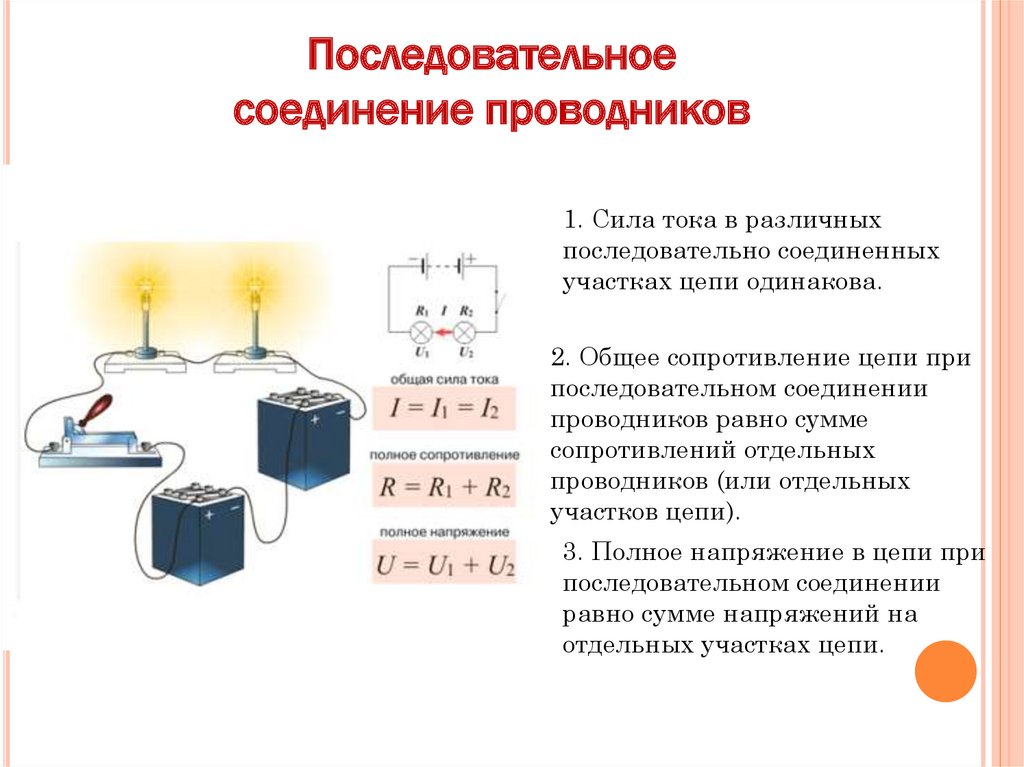
Конденсатор c1

Конденсатор состоит из двух пластин или обкладок , находящихся одна перед другой и сделанных из проводящего материала. Между пластинами находится изолирующий материал, называемый диэлектриком рис. Простейшими диэлектриками являются воздух, бумага, слюда и т. Зарядка конденсатора. Основным свойством конденсатора является его способность запасать электрическую энергию в виде электрического заряда.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Конденсаторы соединены в батарею, причем C1=C2=2 мкФ, C3=C4=C5=6 мкФ
• I150V614K-C1
• Конденсатор емкости C1 = 1,0 мкФ, предварительно. ..
• Территория электротехнической информации WEBSOR
• Сборник идеальных эссе по обществознанию
• Модуль поддержания напряжения уменьшает емкость буферного конденсатора на 80%
• Последовательное соединение конденсаторов
• Последовательное и параллельное соединение конденсаторов

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Осциллограф С1-73 Варварский разбор. Снова ломаем технику

Конденсаторы соединены в батарею, причем C1=C2=2 мкФ, C3=C4=C5=6 мкФ

Заряженный конденсатор C1 1 мкФ включён в последовательную цепь из резистора R Ом, незаряженного конденсатора C2 2 мкФ и разомкнутого ключа К см.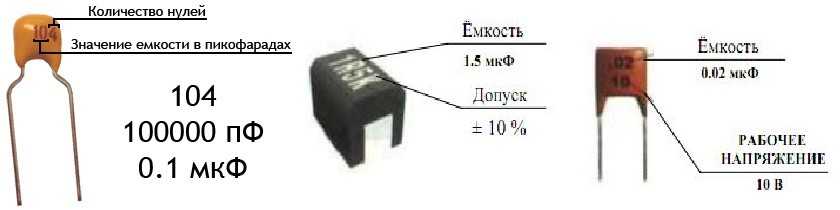 После замыкания ключа в цепи выделяется количество теплоты Q 30 мДж. Чему равно первоначальное напряжение на конденсаторе С1? Сижу над этой задачей три дня уже и вообще не понимаю. Почему заряд не перераспределится даже при выключенном ключе? Ведь один конденсатор заряжен, а другой нет. Что будет, если мы соединим два конденсатора с одинаковым зарядом и емкостями разными полюсами?

Насчет параллельного соединения конденсаторов. Почему напряжение между обкладками эквивалентного конденсатора C равно напряжениям между каждым из конденсаторов в отдельности? Я имею ввиду, что вот есть два конденсатора, с разной емкостью. При одинаковом заряде у них будет разное напряжение между обкладками.

С чего вдруг это напряжение равно напряжению после объединения?? Не совсем в тему, но непонятно, почему в колебательном контуре заряд уменьшается из-за трат на тепло? Куда исчезают заряды? Но куда заряды исчезают? Когда конденсатор разряжаем через резистор — такого вопроса не возникает. Re: Заряженный конденсатор включён в последовательную цепь.

Последний раз редактировалось rustot Текст или формулы замещены рисунками. Подробно Forum Administration в сообщении писал а :. Нарушения и санкции 1 Нарушением считается: м Набор любых формул без использования системы набора краткие инструкции по набору можно прочесть здесь , здесь или здесь.

Использование картинок в качестве замены текста и формул за исключением геометрических чертежей, сложных диаграмм и таблиц. Несоблюдение правил использования внешних ссылок см. Заряженный конденсатор включён в последовательную цепь Re: Заряженный конденсатор включён в последовательную цепь Тут есть путаница, связанная с тем что «зарядом» называют разные вещи, хотя и обозначают одинаково и единицы измерения те же самые и даже соотношения в которых он участвует очень похожи.

Заряд проводника — это сумма всех имеющихся в нем зарядов, положительных и отрицательных, если эта сумма нулевая то заряд равен нулю. Суммарный заряд конденсатора может быт равен нулю, но «зарядом конденсатора» называют модуль заряда одного из его проводников и он может быть при этом нулю не равен Заряд системы в первом смысле измениться не может кроме как путем перемещения заряда извне системы.

Но «заряд» во втором смысле может свободно меняться.

Переместили заряд с одного проводника конденсатора на другой — суммарный заряд не изменился, но поскольку мы теперь «зарядом» называем модуль заряда только одного из них — он изменился.

Posted automatically Подробно Forum Administration в сообщении писал а : I. Наберите все формулы и термы ом. Инструкции по оформлению формул здесь или здесь или в этом видеоролике.

После исправлений сообщите в теме Сообщение в карантине исправлено , и тогда тема будет возвращена. Страница 1 из 1.

I150V614K-C1

Теория и практика. Кейсы, схемы, примеры и технические решения, обзоры интересных электротехнических новинок. Уроки, книги, видео. Профессиональное обучение и развитие. Сайт для электриков и домашних мастеров, а также для всех, кто интересуется электротехникой, электроникой и автоматикой.

Решение Батарея из четырёх конденсаторов электроёмкостью C1 = 2C, C2 = C, C3 = 4C и C4 = 2C подключена к источнику постоянного тока с.

Конденсатор емкости C1 = 1,0 мкФ, предварительно…

Идея устройства взята из статьи «Микрофарадметр» А. Принцип работы устройства заключается в измерении времени заряда измеряемого конденсатора заданным током до опорного напряжения. Приставка имеет два поддиапазона измерения: Время измерения конденсаторов ёмкостью до мкФ не превышает 1,5с, до мкФ — 3с. Время измерения конденсатора максимальной ёмкости не превышает 12с. Относительно большое время измерения связано с ограниченной мощностью источника питания МК Если сразу после этого напряжение на конденсаторе превысит 1В низкий логический уровень на входе BUSY , считается что конденсатор в обрыве. Как только напряжение на конденсаторе достигнет 1В, по времени заряда рассчитывается ёмкость и прекращается заряд. При достижении напряжения на конденсаторе 1В ёмкость рассчитывается как для первого поддиапазона.

Территория электротехнической информации WEBSOR

У многих радиолюбителей, особенно приступающих впервые к конструированию электросхем, возникает вопрос, как надо подключить конденсатор требуемой ёмкости? Когда, к примеру, в каком-то месте схемы нужен конденсатор ёмкостью мкФ, и такой элемент есть в наличии, то проблемы не возникнет. Но когда требуется поставить конденсатор на мкФ, а присутствуют только элементы неподходящей емкости, на помощь приходят схемы из нескольких конденсаторов, соединённых вместе. Соединять элементы можно, применяя параллельное и последовательное соединение конденсаторов по отдельности или по комбинированному принципу.

Простой пример.

Сборник идеальных эссе по обществознанию

By Calligraff , November 19, in Радиоэлементы. Мы принимаем формат Sprint-Layout 6! Экспорт в Gerber из Sprint-Layout 6. Конденсаторы Panasonic. Часть 4.

Модуль поддержания напряжения уменьшает емкость буферного конденсатора на 80%

Изобретение касается электронных схем, предназначенных для преобразования электрической энергии, установок электропитания, в которых они используются. На фиг. Один полюс каждого из двух выключателей образует часть пары расположенных выше по потоку полюсов, а другой полюс каждого выключателя образует часть пары расположенных ниже по потоку полюсов, причем пара находящихся ниже по потоку полюсов расположенной выше по потоку ячейки соединена с парой находящихся выше по потоку полюсов расположенной ниже по потоку ячейки. Пара находящихся выше по потоку полюсов первой ячейки CL1 подсоединена к источнику тока C, тогда как пара находящихся ниже по потоку полюсов последней ячейки CLn. Преобразователь содержит также конденсаторы C1, C2, Каждый конденсатор подсоединен между двумя полюсами, составляющими пару находящихся ниже по потоку полюсов ячейки. Преобразователь дополнительно имеет средство управления не показанное , управляющее нормальной работой преобразователя и действующее на выключатели последующей ячейки таким образом, что два выключателя любой одной ячейки всегда находятся в соответственных противоположных состояниях электропроводности представленных линиями управления типа lc1. Под действием сигнала управления, подаваемого упомянутым средством управления, один из двух выключателей в данной ячейке последовательно находится в первом состоянии электропроводности, а затем во втором состоянии электропроводности во время циклически повторяющихся периодов работы преобразователя.

Найди ответ на свой вопрос: Емкость некоторого участка цепи, содержащей конденсатор С1=2 мкФ, необходимо увеличить до С2=3.

Последовательное соединение конденсаторов

Конденсатор , в народе именуемый кондером, является средством накопления электроэнергии в электрических цепях. Типичной областью применения являются: сглаживающие фильтры в источниках электропитания; цепи межкаскадовых связей; фильтрация помех. Электрическая характеристика конденсатора определяется его конструкцией и средствами используемых материалов. Конденсатор состоит из пластин или обкладок находящихся друг перед другом, сделанных из токопроводящего материала, и изолирующего материала в основном бумага и слюда.

Последовательное и параллельное соединение конденсаторов

ВИДЕО ПО ТЕМЕ: Осциллограф С1-125 (ч.1), разбор [Запись]

При снижении напряжения входной шины авиационное электронное оборудование и военные системы требуют поддержания работоспособности в целях сохранения данных и контролируемого отключения. Для обеспечения этого обычно применяется конденсатор большой емкости, подключенный к входу преобразователей, питающий приборы при снижении напряжения ниже минимального значения или отключении. Не существует никакого максимального ограничения, кроме как длительность времени заряда. Компоненты силовой электроники. Силовые разъемы.

При сборке самодельных электронных схем поневоле сталкиваешься с подбором необходимых конденсаторов. Притом, для сборки устройства можно использовать конденсаторы уже бывшие в употреблении и поработавшие какое-то время в радиоэлектронной аппаратуре.

Выберите город чтобы посмотреть ближайшие пункты выдачи СДЭК. Показать города. Краснов Владимир Леонидович — 09 Октября Заказ шёл до пункта выдачи почти месяц, заказал Заказывал 6 позиций запчасти для Citroen DS3. Два задних фонаря 2.

Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели. При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов. C C1 C2 C3 А общее напряжение будет равняться сумме напряжений всех конденсаторов.

Последовательное и параллельное соединение конденсаторов

Все наверняка уже знают, что собой представляют последовательное и параллельное соединения.
Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным.

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов, получаемая цепь выглядит следующим образом:

Эта схема состоит из следующих элементов:                                                                                          трех конденсаторов C1, C2, С3 и источника электрической энергии E.

Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора C2, ну а конец конденсатора C2 соединен с началом третьего конденсатора C3.
Стоит обратить внимание на то, как распределяются ёмкости каждого.

При таком соединении, все ёмкостя следующим образом.

Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад.
Общую емкость можно рассчитать по следующей формуле:

Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:

Параллельное соединение конденсаторов

При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже:

Так при параллельном соединении, емкости всех конденсаторов складываются:

То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.

Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме.

Смешанное соединение конденсаторов

Смешанное соединение конденсаторов выглядит следующим образом:

И представляет с собой различные сочетания параллельного и последовательного соединений.
Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.
Например, дана следующая схема и следующие данные:

C1=0.4Ф
C2=0.8Ф
C3=0,73Ф
Необходимо найти общую емкость всех трех конденсаторов.
Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.
Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.

Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.

Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость.

[Решено] Три конденсатора C1, C2 и C3 емкостью 10 мкФ, 5

Три конденсатора C ₁ , C ₂ и C ₃ емкостью 10 мкФ, 5 мкФ и 2 мкФ соответственно, имеют пробой 10 В, 5 В и 2 В соответственно. Для соединения, показанного ниже, максимальное безопасное напряжение в Вольтах, которое может быть приложено к комбинации, и соответствующий общий заряд в мкКл, хранящийся в эффективной емкости на клеммах, составляют соответственно

1. 2,8 и 36
2. 7 и 119
3. 2,8 и 32
4. 7 и 80

Вариант 3: 2,8 и 32

БЕСПЛАТНЫЙ

CT 1: Уровень и доля доля

9,7 тыс. пользователей

10 вопросов

16 баллов

30 минут

Предположим, что напряжение на трех конденсаторах C ₁ , C ₂ и C ₃ равно V ₁ , V ₂ и V _{3 90 соответственно. Итак, мы можем написать}

В ₂ /В ₃ = C ₃ /C ₂

Поскольку напряжение обратно пропорционально емкости. Теперь, учитывая, что

C ₁ = 10 мкФ; (V ₁ ) _макс. = 10 В

C ₂ = 5 мкФ; (V ₂ ) _макс. = 5 В

C ₃ = 2 мкФ; (V ₃ ) _max = 2 V

V ₂ /V ₃ = 2/5

Для (V ₃ ) _max = 2

\(% MathType!Translator!2!1!AMS LaTeX.tdl!AMSLaTeX! % MathType!MTEF!2!1!+- % feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacaWGwbWdamaaBaaaleaapeGaaGOmaaWdaeqaaOWdbiabg2da9maa % laaapaqaa8qacaaIYaGaey41aqRaaGOmaaWdaeaapeGaaGynaaaacq % GH9aqpcaaIWaGaaiOlaiaaiIdacaWG2bGaam4BaiaadYgacaWG0bGa % эйипаВЯаГынаааа!4694! {V_2} = \frac{{2 \times 2}}{5} = 0,8 вольт < 5% MathType!End!2!1! \)

В ₂ < (В ₂ ) _max

Следовательно, это напряжение на C ₂ . Следовательно,

V ₃ = 2 Вольт

V ₂ = 0,8 Вольт

V ₁ = V ₂ + V ₃ = 2,8 Вольт

Эквивалентная емкость через терминал = 2,8 Вольт

.0009

\(% MathType!Translator!2!1!AMS LaTeX.tdl!AMSLaTeX! % MathType!MTEF!2!1!+- % feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacaWGdbWdamaaBaaaleaapeGaamyzaiaadghaa8aabeaak8qacqGH % 9aqpdaWcaaWdaeaapeGaam4qa8aadaWgaaWcbaWdbiaaikdaa8aabe % aak8qacaWGdbWdamaaBaaaleaapeGaaG4maaWdaeqaaaGcbaWdbiaa % doeapaWaaSbaaSqaa8qacaaIYaaapaqabaGcpeGaey4kaSIaam4qa8 % aadaWgaaWcbaWdbiaaiodaa8aabeaaaaGcpeGaey4kaSIaam4qa8aa % daWgaaWcbaWdbiaaigdaa8aabeaaaaa!45EB! {C_{eq}} = \frac{{{C_2}{C_3}}}{{{C_2} + {C_3}}} + {C_1}% MathType!Конец!2!1! \)

\(% MathType!Translator!2!1!AMS LaTeX. tdl!AMSLaTeX! % MathType!MTEF!2!1!+- % feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacqGH9aqpdaWcaaWdaeaapeGaaGynaiabgEna0kaaikdaa8aabaWd % biaaiwdacqGHRaWkcaaIYaaaaiabgUcaRiaaigdacaaIWaGaeyypa0 % ZaaSaaa8aabaWdbiaaiIdacaaIWaaapaqaa8qacaaI3aaaaiabeY7a % TjaadAeaaaa!45C3! = \frac{{5 \times 2}}{{5 + 2}} + 10 = \frac{{80}}{7}\mu F% MathType!End!2!1! \)

Эквивалентное напряжение составляет (max.value)

V _MAX = V ₁ = 2,8

Таким образом, заряд, хранящийся в эффективной емкости

Q = C _EQ V _Max

_{\ (% MathType!Translator!2!1!AMS LaTeX.tdl!AMSLaTeX! % MathType!MTEF!2!1!+- % feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8 % qacqGH9aqpdaqadaWdaeaapeWaaSaaa8aabaWdbiaaiIdacaaIWaaa % paqaa8qacaaI3aaaaaGaayjkaiaawMcaamaabmaapaqaa8qacaaIYa % GaaiOlaiaaiIdaaiaawIcacaGLPaaacqGH9aqpcaaIZaGaaGOmaiaa % cckacqaH8oqBcaWGdbaaaa!4549! = \left( {\frac{{80}}{7}} \right)\left( {2. 8} \right) = 32\;\mu C% MathType!End!2!1! \)}

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления GATE EE

Последнее обновление: 11 октября 2022 г.

Экзамен GATE EE 2023 запланирован на 28 ноября 2022 г. Экзамен будет проводиться 5 февраля 2023 г. в утреннее время с 9:30 до 12:30. Карта допуска GATE EE будет доступна с 3 января 2023 г., ключ ответа будет доступен с 21 февраля 2023 г., а результат будет получен 21 марта 2023 г. Индийский технологический институт Канпур выпустил новое уведомление для GATE EE 2023. Кандидаты, готовящиеся к экзамену, могут обратиться к важным вопросам GATE EE, чтобы улучшить свою подготовку к экзамену и повысить свои шансы на отбор.

Конденсатор ${C_1} = 1\,\mu F$ заряжают до напряжения $V = 60\,V$, подключив его к батарее $B$ через переключатель $\left( 1 \right) $. Теперь ${C_1}$ отключается от батареи и подключается к цепи, состоящей из двух незаряженных конденсаторов ${C_2} = 3\,\mu F$ и ${C_3} = 6\,\mu F$ через переключатель $\ left( 2 \right)$ как показано на рисунке.

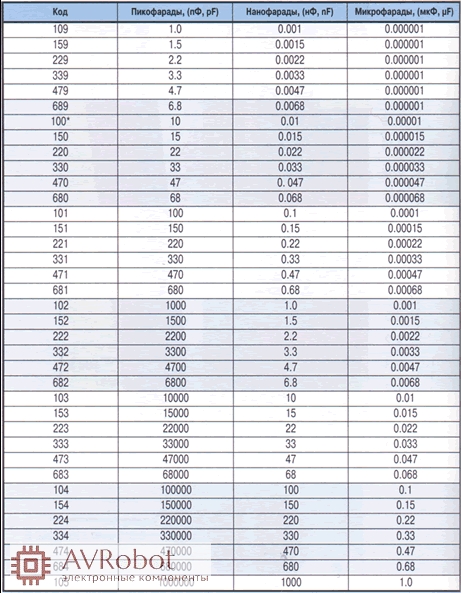Сумма конечных зарядов ${C_2}$ и ${C_3}$ равна: (A) $40\,\mu C$(B) $36\,\mu C$(C) $20\,\mu C$( D) $54\,\mu C$

Подсказка: Сумма окончательных сборов ${C_2}$ и ${C_3}$ может быть определена по двум формулам. Конденсатор — это формула серии, а затем разность потенциалов в формуле конденсатора. Используя данную информацию в этих двух формулах, можно определить сумму окончательных расходов ${C_2}$ и ${C_3}$.

Используемые формулы:
Конденсатор последовательно,
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
Где $C$ — эквивалентная емкость, ${C_1}$ — емкость первого конденсатора, а ${C_2}$ — емкость второго конденсатора.
Разность потенциалов в конденсаторе,
$V = \dfrac{Q}{C}$
Где $V$ — разность потенциалов, $Q$ — заряд, а $C$ — емкость.

  Полное пошаговое решение:
Учитывая, что
Конденсатор А, ${C_1} = 1\,\mu F$
Напряжение $V = 60\,V$
Емкость равна, ${C_2 } = 3\,\mu F$ и ${C_3} = 6\,\mu F$
Конденсатор включен последовательно, а конденсаторы ${C_2}$ и ${C_3}$ включены последовательно, тогда
$\dfrac {1}{C} = \dfrac{1}{{{C_2}}} + \dfrac{1}{{{C_3}}}\,. ……….. ..\влево( 1 \вправо)$
Переставив члены, приведенное выше уравнение запишется как
$\dfrac{1}{C} = \dfrac{{{C_3} + {C_2}}}{{{C_3} \times {C_2}}} $
Если принять обратное выражение от обеих частей приведенного выше уравнения, то приведенное выше уравнение запишется как
$C = \dfrac{{{C_3} \times {C_2}}}{{{C_3} + {C_2}}} $
Подставляя данные термины в приведенное выше уравнение, тогда
$C = \dfrac{{6 \times 3}}{{6 + 3}}$
При дальнейшем упрощении, тогда
$C = \dfrac{{ 18}}{9}$
При делении вышеприведенное уравнение записывается как
$C = 2\,\mu F$
Теперь разность потенциалов между тремя конденсаторами ${C_1}$ и $C$ (здесь $C$ – суммарная емкость конденсаторов ${C_2}$ и ${C_3}$. )
$V = \dfrac{Q}{{{C_1} + C}}$
Если подставить заряд и емкость в приведенное выше уравнение, то
$V = \dfrac{{60}}{{1 + 2 }}$
При дальнейшем упрощении, тогда
$V = \dfrac{{60}}{3}$
При делении слагаемых в предыдущем уравнении, тогда
$V = 20\,V$
Сумма заряда конденсаторов ${C_2}$ и ${C_3}$,
$Q = C \times V$ (Здесь $C$ — суммарная емкость ${C_2}$ и ${C_3}$ )
Теперь подставим суммарную емкость ${C_2}$ и ${C_3}$ , и разность потенциалов $V$ в приведенном выше уравнении, тогда
$Q = 2 \times 20$
При умножении, тогда
$Q = 40\,\mu C$
Таким образом, приведенное выше уравнение показывает сумму окончательные расходы ${C_2}$ и ${C_3}$.