Конденсатор рисунок. Конденсатор: устройство, принцип работы и применение в электротехнике — Производство и поставка электростанций, Бензиновые и дизельные генераторы от 1 до 100 кВт. Мини ТЭЦ на базе двигателя Стирлинга.

Что такое конденсатор и как он работает. Из чего состоит конденсатор. Какие бывают виды конденсаторов. Как рассчитать емкость конденсатора. Где применяются конденсаторы в электронике и технике.

Содержание

Что такое конденсатор и его устройство

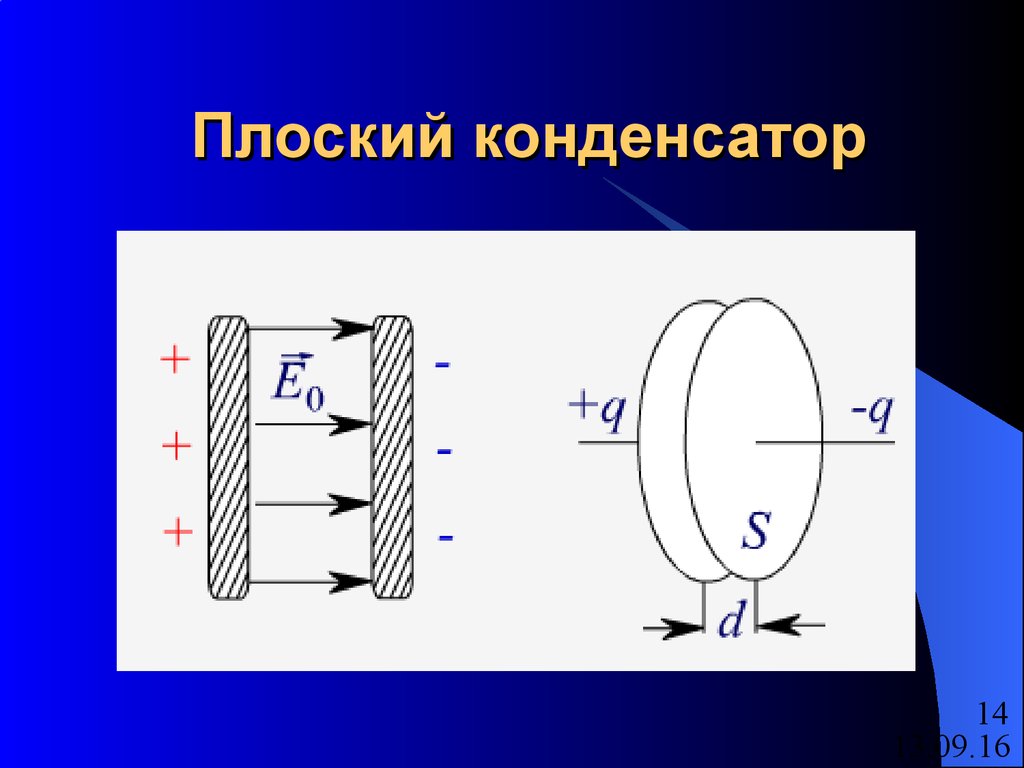
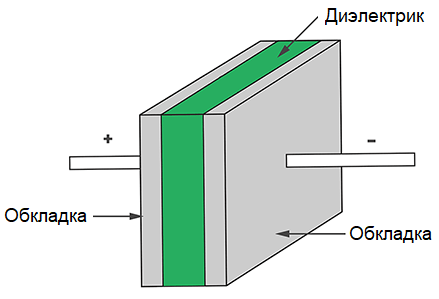
Конденсатор — это электронный компонент, способный накапливать и хранить электрический заряд. Простейший конденсатор состоит из двух проводящих пластин (обкладок), разделенных диэлектриком:

Обкладки — металлические пластины, на которых накапливается заряд
Диэлектрик — непроводящий материал между обкладками (воздух, керамика, пластик и др.)

При подключении конденсатора к источнику напряжения на одной обкладке накапливаются положительные заряды, на другой — отрицательные. Между обкладками возникает электрическое поле.

Как работает конденсатор

Принцип работы конденсатора основан на способности накапливать и отдавать электрический заряд. Как это происходит?

При подключении к источнику тока конденсатор заряжается — на обкладках накапливаются заряды

После отключения источника заряд сохраняется на обкладках
При замыкании цепи происходит разряд конденсатора — заряды перетекают с одной обкладки на другую

Таким образом, конденсатор может накапливать энергию электрического поля и затем отдавать ее в цепь.

Основные характеристики конденсаторов

Главной характеристикой конденсатора является электрическая емкость. Она показывает, какой заряд накапливает конденсатор при заданном напряжении:

C = Q / U

где C — емкость, Q — заряд, U — напряжение.

Емкость измеряется в фарадах (Ф). Типичные значения — от пикофарад (пФ) до микрофарад (мкФ).

Другие важные параметры конденсаторов:

Рабочее напряжение — максимальное напряжение, которое выдерживает конденсатор
Температурный коэффициент емкости — изменение емкости при нагреве/охлаждении

Тангенс угла диэлектрических потерь — показатель энергетических потерь в диэлектрике

Виды конденсаторов

Существует множество типов конденсаторов, различающихся конструкцией и применяемыми материалами:

Керамические — компактные, для высоких частот
Электролитические — большая емкость, полярные
Пленочные — стабильные характеристики
Слюдяные — для высоковольтных цепей
Танталовые — миниатюрные, для поверхностного монтажа
Подстроечные — с регулируемой емкостью

Выбор типа конденсатора зависит от требуемых параметров и условий эксплуатации.

Расчет емкости конденсатора

Емкость плоского конденсатора можно рассчитать по формуле:

C = ε * ε0 * S / d

где ε — диэлектрическая проницаемость среды между обкладками, ε0 — электрическая постоянная, S — площадь обкладок, d — расстояние между ними.

От чего зависит емкость конденсатора?

Прямо пропорциональна площади обкладок
Обратно пропорциональна расстоянию между обкладками
Зависит от свойств диэлектрика

Применение конденсаторов в электронике

Конденсаторы широко используются в электронных устройствах и электрических цепях для различных целей:

Накопление энергии и сглаживание пульсаций в источниках питания
Разделение постоянной и переменной составляющих сигнала
Фильтрация высокочастотных помех
Создание колебательных контуров в радиотехнике
Блокировка самовозбуждения усилителей
Запуск электродвигателей

Без конденсаторов невозможно представить современную электронику и электротехнику.

Соединение конденсаторов

В электрических схемах конденсаторы могут соединяться последовательно или параллельно:

Последовательное соединение

При последовательном соединении:

Общий заряд равен заряду на каждом конденсаторе
Напряжения складываются
Обратные величины емкостей складываются: 1/C = 1/C1 + 1/C2 + …

Параллельное соединение

При параллельном соединении:

Напряжение на всех конденсаторах одинаково
Заряды складываются
Емкости складываются: C = C1 + C2 + …

Зная эти правила, можно рассчитать параметры сложных конденсаторных сборок.

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией электрического поля. Ее можно рассчитать по формуле:

W = CU^2 / 2 = Q^2 / (2C)

где W — энергия, C — емкость, U — напряжение, Q — заряд.

Эта энергия может быть преобразована в другие виды, например:

Тепловую — при разряде на резистор
Механическую — в электростатических двигателях
Световую — при искровом разряде

Способность запасать энергию делает конденсаторы незаменимыми во многих устройствах.

Конденсатор в автосигнализации

Рисунок 22. Конденсаторы различных типов и марок

Рисунок 23. Условное обозначение конденсатора

Само название «конденсатор» означает «накопитель».

Что он накапливает? Конденсатор накапливает электрический заряд и хранит в себе некоторое время время (до нескольких десятков часов). В этом отношении конденсатор можно сравнить с аккумулятором — тот также сперва собирает заряд, а потом отдает его по мере надобности.

Рисунок 24. Заряд и разряд конденсатора

В аккумуляторе накопление энергии происходит за счет сложных химических реакций, а в конденсаторе ничего подобного нет. В прямом смысле, лучший конденсатор — это токопроводящие пластины в вакууме. Но поскольку добиться идеальной пустоты (вакуума) сложно, самым простым конденсатором является устройство, состоящее из двух металлических пластин и воздушного промежутка между ними. Если пластины подключить к источнику питания, конденсатор накопит заряд. Затем, если вместо источника подсоединить, например, электрическую лампу, то она какое-то время будет светиться за счет запасенного в конденсаторе электричества. В настоящее время вместо воздуха в конденсаторах используют твердые диэлектрики (вещества, не проводящие электрический ток).

Рисунок 25. Устройство конденсатора

Отметим одно из важных свойств конденсатора — он не пропускает через себя постоянный ток. Переменный ток условно способен проходить через конденсатор.

Почему так происходит? Попробуем разобраться.

При включении разряженного конденсатора в электрическую цепь постоянного тока, он сразу же начнет заряжаться. При этом в цепи потечет ток, носители заряда будут скапливаться на пластинах конденсатора. По мере заряда частицам на обкладках становится «тесно», количество частиц, дополнительно попадающих на обкладки, уменьшается. Следовательно, ток в цепи также уменьшается. Как только «все места» на обкладках будут «заняты», ток прекратится.

Этот процесс можно сравнить с заполнением пустого автобуса на конечной остановке — как только открываются двери, внутрь врывается толпа пассажиров. Когда все сидячие и стоячие (и висячие) места заполнятся, внутрь не проникнет больше ни один пассажир, хотя на остановке их еще осталось достаточно много. Так же и в нашей цепи — несмотря на то, что цепь подключена к источнику, тока в ней после заряда конденсатора не будет.

Рисунок 26. Конденсатор и постоянный ток

В рассматриваемой цепи течет переменный ток, меняющий направление. В процессе заряда конденсатора в определенный момент направление тока меняется и начинается разряд конденсатора, а затем — его заряд, но уже противоположной полярности. Такие колебания будут происходить до тех пор, пока в цепи будет работать источник переменного тока. Таким образом, в каждый момент времени в цепи с переменным током и конденсатором постоянно наблюдается движение электронов, то есть течет ток.

Рисунок 27. Конденсатор и переменный ток

Это свойство конденсатора позволяет использовать его, например, для отделения постоянной составляющей электрического тока от переменной.

Основная характеристика конденсатора — емкость. Как и в случае с любой другой емкостью (например, канистрой), емкость конденсатора можно представить в виде его «вместимости», то есть: чем больше эта емкость, тем больше энергии сможет запасти в себе конденсатор.

Измеряется емкость в Фарадах, однако один Фарад — это очень большая емкость, поэтому чаще используют производные величины.

Таблица 11. Единицы емкости

1 мкФ (один микрофарад, uF) = 0,000 001 Ф (одна миллионная фарада)

1 нФ (один нанофарад, nF) = 0,001 мкФ (одна тысячная микрофарада)

1 пФ (один пикофарад, pF) = 0,000 001 мкФ (одна миллионная микрофарада)

В автомобильной аудиотехнике применяются специальные конденсаторы с емкостью в единицы (до 15) фарад, позволяющие компенсировать провалы напряжения питания на большой громкости.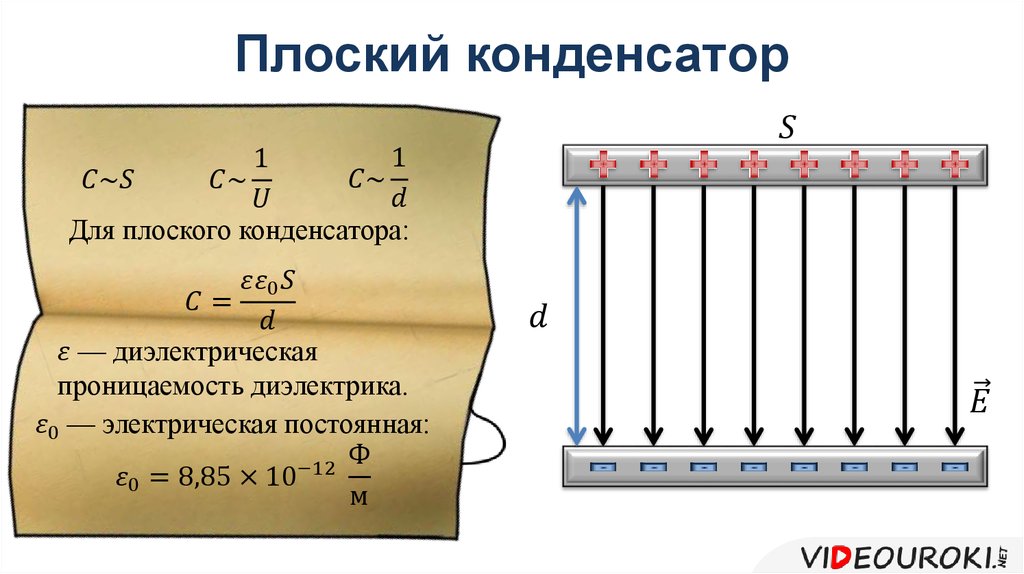

Конденсаторы бывают полярными и неполярными. Полярные требуют соблюдения полярности подключения: чтобы вывод, отмеченный плюсом, был подключен именно к плюсу, а не к минусу. Что произойдет, если этого не соблюсти? Конденсатор выйдет из строя. Причем конденсатор «заявит» об этом громким хлопком и разбрызгиванием своего содержимого во все стороны. Поэтому старайтесь соблюдать маркировку на корпусе конденсатора и печатной плате (на всех платах в местах установки полярных конденсаторов нанесена полярность его подключения).

Рисунок 28. Полярный конденсатор

Неполярный конденсатор избавлен от этого недостатка, его можно включать в цепь, не задумываясь о соблюдении полярности.

Рисунок 29. Неполярные конденсаторы

Но отказаться от полярных конденсаторов полностью невозможно, так как все конденсаторы большой емкости — исключительно полярные.

Второй важный параметр конденсатора — рабочее напряжение. Поскольку между обкладками (пластинами) конденсатора находится тонкий слой диэлектрика, то превышение указанного напряжения может привести к электрическому пробою (короткому замыканию) внутри конденсатора и выходу его из строя.

Неправильно выбранное рабочее напряжение конденсатора приводит к выходу его из строя или даже взрыву!

Рисунок 30. Взорвавшийся конденсатор

При выборе номинального напряжения конденсатора следует делать некоторый запас, то есть для цепи 12 В подойдет конденсатор, на котором написано, например, 16 В. Для этой же цепи можно взять конденсатор и на 25 В, но он, как правило, дороже и крупнее

На полярных конденсаторах большой емкости (>10 000 мкФ), непосредственно на корпусе указываются напряжение и полярность подключения, на неполярных — как правило, только емкость.

Конденсаторы в электронике используются как составная часть электрических фильтров, резонансных контуров и разделительных элементов в усилительных каскадах. Вместе с сопротивлением они используются как времязадающая цепь в генераторах и таймерах.

При монтаже автомобильных охранных систем конденсатор может использоваться, например, как замедлитель срабатывания или отпускания реле, чтобы реализовать небольшую задержку срабатывания. Или при подключении цепей контроля запуска двигателя для отсеивания постоянной составляющей тока от переменной.

Рисунок 31. Схема-подсказка «Конденсатор»

Конденсаторы | 8 класс | Физика

Содержание

Если тело обладает некоторым электрическим зарядом, то вокруг него обязательно присутствует электрическое поле. Это поле обладает некоторой энергией — может совершить какую-то работу.

Можно ли как-то накопить эту энергию? Да, такая возможность существует. Для этого используют специальный прибор — конденсатор.

Конденсатор — это устройство, позволяющее накапливать электрические заряды и, соответственно, энергию электрического поля.

На данном уроке вы познакомитесь с устройством этого прибора, его характеристиками и свойствами.

{"questions":[{"content":"Конденсатор — это прибор для[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["накопления энергии электрического поля","измерения энергии электрического поля","регулировки силы тока в цепи"],"explanations":["","","Эту функцию выполняют реостаты."],"answer":[0]}}}]}

Простейший конденсатор и его устройство

Устройство простейшего конденсатора представлено на рисунке 1. Он состоит из двух одинаковых металлический пластин. Эти пластины называются обкладками конденсатора.

Обкладки расположены на небольшом расстоянии друг от друга. Этот промежуток между ними обязательно должен быть заполнен слоем диэлектрика. В нашем случае таким диэлектриком является обычный воздух.

Такой конденсатор называется плоским (по форме обкладок).

Конденсатор имеет свой условный знак для обозначения на схеме электрической цепи (рисунок 2).

{"questions":[{"content":"Между обкладками конденсатора обязательно должен присутствовать[[choice-9]]","widgets":{"choice-9":{"type":"choice","options":["слой диэлектрика","проводник","защитный слой"],"answer":[0]}}}]}

Зарядка конденсатора и его способность накапливать заряды

Теперь разберемся, каким же образом мы можем накапливать заряды с помощью конденсатора.

Рассмотрим простой опыт. Возьмем конденсатор, состоящий из двух металлических пластин, расположенных параллельно друг другу, и заряженный аккумулятор.

Две обкладки конденсатора подключим к разным полюсам аккумулятора. На обкладках начнут образовываться электрические заряды (рисунок 3). Они будут равны друг другу, но иметь противоположные знаки.

Эти заряды образуют электрическое поле конденсатора. Оно будет сосредоточено между обкладками.

Отключим аккумулятор от конденсатора. Что мы увидим? Заряды, образованные на обкладках, никуда не деваются. Они сохраняются, как и электрическое поле между пластин. Конденсатор заряжен.

Если мы соединим проводником обкладки конденсатора, то увидим, что по нему некоторое время будет течь ток. Значит, заряженный конденсатор является источником тока в электрической цепи.

{"questions":[{"content":"Какой конденсатор может быть источником тока в электрической цепи?[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["Заряженный","любой","разряженный","Плоский"],"answer":[0]}}}]}

Электроемкость конденсатора

Логично предположить, что разные конденсаторы по-разному будут накапливать заряд. Как охарактеризовать эту способность прибора? Для этого существует специальная величина — электроемкость (или просто емкость) конденсатора.

Чтобы понять смысл этой величины, рассмотрим опыт. Возьмем две металлические пластины и установим их на изолированных подставках друг напротив друга.

Подключим к пластинам электрометр. Этот прибор (рисунок 4) по своему устройству и принципу действия схож с электроскопом. Он позволит нам зафиксировать значения напряжения, которое возникнет между пластинами.

Итак, одну из пластин (A) мы соединим проводом со стержнем электрометра, а другую (B) соединим с корпусом прибора (заземлим). Коснемся положительно наэлектризованной стеклянной палочкой внешней стороны пластины A (рисунок 5).

Мы сообщили пластине A положительный заряд $+q$. Вокруг этого заряда (пластины A) теперь существует электрическое поле. Под его действием произойдет перераспределение зарядов в пластине B.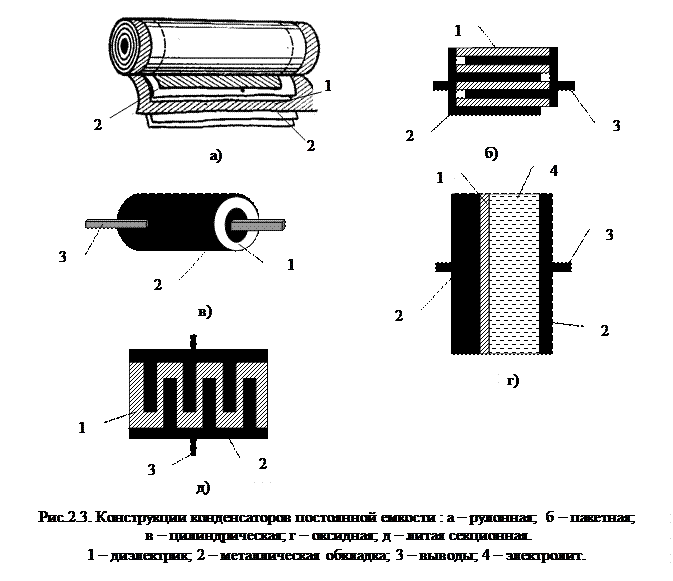 Отрицательные заряды перейдут на внутреннюю сторону пластины, а положительные — на внешнюю.

Помните, что мы заземлили пластину B? За счет этого на пластину пойдут свободные электроны с земли. Они нейтрализуют положительный заряд на внешней стороне пластины. Таким образом, мы получили на пластине B отрицательный заряд $-q$ (рисунок 6). По величине он равен заряду на другой пластине.

Стрелка электрометра отклонилась. Зафиксируем это значение напряжения между пластинами. Далее мы снова сообщим заряд пластине B, равный по величине первому сообщаемому заряду. Потом сообщим третий и четвертый такие же заряды, наблюдая за стрелкой электрометра.

Вы увидите, что при увеличении заряда в 2, 3, 4 раза, соответственно, в 2, 3, 4 раза увеличиваются показания электрометра — напряжение между пластинами. Важно отметить, что отношение заряда к напряжению при этом будет постоянно:
$\frac{q}{U} = \frac{2q}{2U} = \frac{3q}{3U} = \frac{4q}{4U} = const$.

Теперь мы можем дать определение электроемкости конденсатора.

Электроемкость конденсатора — это величина, измеряемая отношением заряда на одной из пластин конденсатора к напряжению между пластинами:
$C = \frac{q}{U}$.

{"questions":[{"content":"Электроемкость конденсатора определяется отношением[[choice-16]]","widgets":{"choice-16":{"type":"choice","options":["заряда к напряжению между обкладками","напряжения между обкладками к заряду","заряда на одной обкладке к заряду на другой"],"explanations":["","","Эти заряды равны, но противоположны друг другу по знаку. За заряд конденсатора мы принимаем численное значение заряда одной из обкладок."],"answer":[0]}}}]}

Единицы измерения электроемкости

В СИ электроемкость измеряется в фарадах ($Ф$).

Электроемкость конденсатора равна единице, если при сообщении ему заряда в $1 \space Кл$ возникает напряжение, равное $1 \space В$ (рисунок 7):
$1 \space Ф = \frac{1 \space Кл}{1 \space В}$. {-12} \space Ф$.

{"questions":[{"content":"Электроемкость измеряется в[[choice-24]]","widgets":{"choice-24":{"type":"choice","options":["фарадах","ньютонах","амперах","ваттах"],"explanations":["","Это единица измерения силы.","Это единица измерения силы тока.","Это единица измерения мощности тока."],"answer":[0]}}}]}

Зависимость электроемкости от площади пластин конденсатора

От чего зависит электроемкость? Начнем с размера пластин.

Зафиксируем полученное в первом опыте с электрометром и конденсатором значение напряжения $U_1$. Теперь возьмем пластины, имеющие большую площадь. Сообщим им точно такой же заряд $q$ (рисунок 9).

Мы увидим, что стрелка электрометра отклоняется меньше. Это означает, что напряжение между этими пластинами меньше напряжения между пластинами меньшей площади ($U_1 > U_2$).

Из определения электроемкости:
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.

Чем больше площадь пластин, тем больше электроемкость конденсатора.

{"questions":[{"content":"Если мы уменьшим площадь обкладок конденсатора, то его электроемкость[[choice-31]]","widgets":{"choice-31":{"type":"choice","options":["уменьшится","увеличится","не изменится"],"answer":[0]}}}]}

Зависимость электроемкости от расстояния между пластинами конденсатора

Снова обратимся к опыту. Теперь изменим расстояние между пластинами — уменьшим его (рисунок 10).

Мы увидим, что напряжение между пластинами уменьшилось: $U_2 < U_1$. Значит,
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.

При уменьшении расстояния между пластинами конденсатора и при неизменном заряде электроемкость конденсатора увеличивается.

{"questions":[{"content":"Один из способов уменьшить емкость конденсатора — это [[choice-34]]","widgets":{"choice-34":{"type":"choice","options":["увеличить расстояние между его обкладками","уменьшить расстояние между его обкладками","увеличить площадь его обкладок"],"answer":[0]}}}]}

Зависимость электроемкости от диэлектрика

Проведем еще один опыт. Зафиксируем значение напряжения между пластинами конденсатора. Затем внесем между ними лист из оргстекла (рисунок 11). Он является диэлектриком.

Если раньше диэлектриком между пластинами являлся только воздух, то теперь это и воздух, и лист оргстекла. Напряжение между пластинами уменьшилось: $U_1 > U_2$. Значит,
$C_1 = \frac{q}{U_1}$,
$C_2 = \frac{q}{U_2}$,
$C_2 > C_1$.

При внесении диэлектрика электроемкость конденсатора увеличивается.

{"questions":[{"content":"Если добавить еще один слой диэлектрика между обкладками конденсатора, то его емкость[[choice-37]]","widgets":{"choice-37":{"type":"choice","options":["увеличится","уменьшится","не изменится"],"answer":[0]}}}]}

Виды конденсаторов

Между обкладками конденсатора могут быть помещены разнообразные диэлектрики. В зависимости от природы этого диэлектрика конденсаторы разделяют на несколько видов: с твердым, жидким и газообразным диэлектриком.

Также существует классификация и по форме обкладок. Конденсаторы бывают плоские, цилиндрические, сферические (рисунок 12) и др.

Конденсаторы бывают с постоянной емкостью и с переменной емкостью. В последних можно регулировать параметры, от которых зависит емкость — ширину пластин и расстояние между ними.

На данный момент существует огромное разнообразие конденсаторов (рисунок 13). Многие из них носят названия, происходящие от названий материалов, составляющих их: слюдяные, керамические, алюминиевые электролитические, танталовые электролитические, конденсаторы на полимерной пленке.

{"questions":[{"content":"Если конденсатор имеет плоские обкладки, параллельные друг другу, его называют[[choice-40]]","widgets":{"choice-40":{"type":"choice","options":["плоским","квадратным","параллельным","прямоугольным"],"answer":[0]}}}]}

Энергия конденсатора и работа его электрического поля

Заряженный конденсатор обладает некоторой энергией.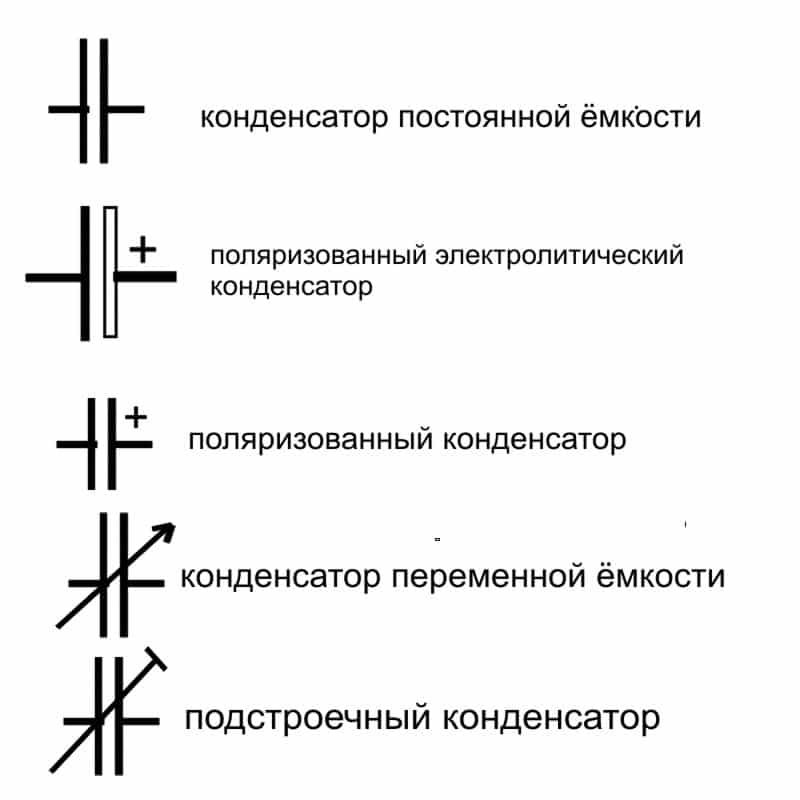 Это легко проверить на опыте. Если мы подключим к конденсатору электрическую лампочку, то она она ярко вспыхнет (рисунок 14). Энергия конденсатора превратилась во внутреннюю энергию нити накаливания лампы и соединительных проводов.

Откуда взялась эта энергия? Конденсатор получает ее при зарядке.

Для того, чтобы зарядить конденсатор, нужно совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии совершенная работа A и будет равна энергии конденсатора E:
$A = E$.

Для расчета такой работы электрического поля конденсатора существует специальная формула.

$A = qU_{ср}$,
где $U_{ср}$ — среднее значение напряжения.

В процессе разрядки напряжение постоянно падает, поэтому нам и необходимо знать для расчетов его среднее значение:
$U_{ср} = \frac{U}{2}$.

Тогда,
$A = qU_{ср} = \frac{qU}{2}$. 2}{2}$»,»$A = qU$»],»answer»:[0]}}}]}

Это свойство (накопление энергии и ее быстрая отдача) широко применяется в различных электронных устройствах, в медицинской технике (рентген, устройства для электротерапии), при изготовлении дозиметров, фотосъемке.

Последовательное соединение конденсаторов

В электрической цепи может быть не один, а сразу несколько конденсаторов. Они могут быть соединены как последовательно, так и параллельно.

Рассмотрим первый тип соединения — последовательный (рисунок 15).

Обкладки 2 и 3, принадлежащие разным конденсаторам, будут являться отдельной деталью. По закону сохранения заряда, заряды на обкладках 2 и 3 будут равны друг другу по модулю, но противоположны по знаку. Из этого следует, что общий заряд конденсаторов численно будет равен заряду на любой из обкладок конденсаторов.

$q = q_1 = q_2 = … = q_n$

Напряжение на концах участка цепи с последовательно соединенными конденсаторами будет складываться из значения напряжений на каждом конденсаторе.

$U = U_1 + U_2 + … + U_n$

Чтобы получить формулу для общей емкости конденсаторов, последнее равенство нужно разделить на заряд q (любой, так как они равны).

$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + … \frac{1}{C_n}$.

{"questions":[{"content":"Общий заряд последовательно соединенных конденсаторов равен[[choice-49]]","widgets":{"choice-49":{"type":"choice","options":["заряду на любой из обкладок конденсаторов","сумме зарядов на всех обкладках конденсаторов","сумме зарядов на двух обкладках одного конденсатора"],"answer":[0]}}}]}

Параллельное соединение конденсаторов

Параллельное соединение конденсаторов показано на рисунке 16.

В этом случае выходы от источника питания будут соединены с каждой обкладкой конденсаторов. Поэтому напряжение на концах такого участка цепи будет равно напряжению между обкладками любого из конденсаторов.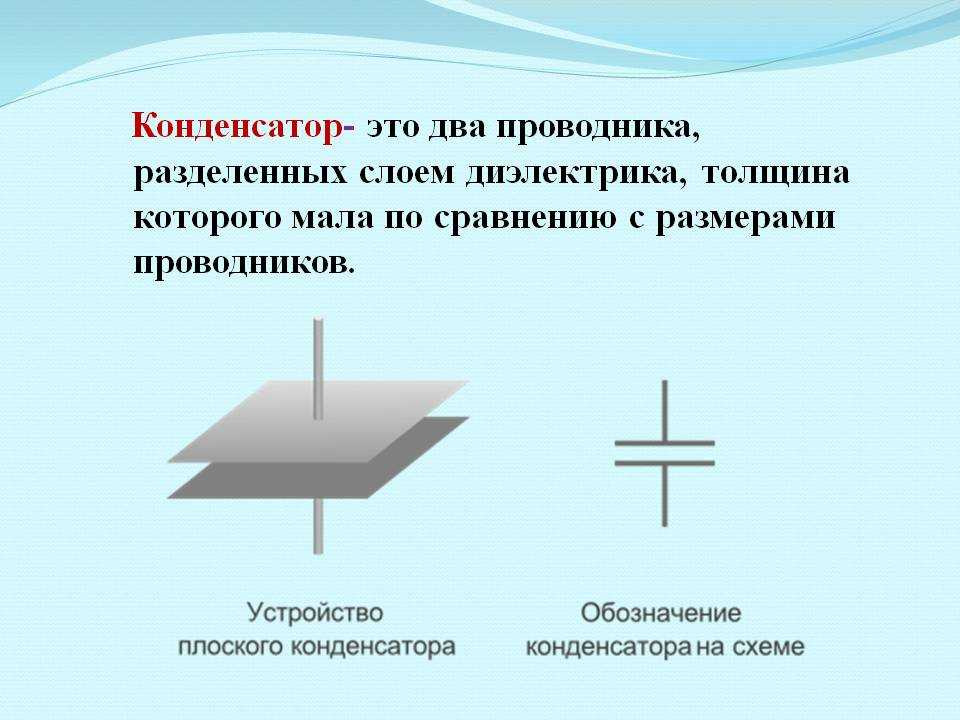

$U = U_1 = U_2 = … = U_n$

Заряды на обкладках будут суммироваться.

$q = q_1 + q_2 + … + q_n$

Разделим это равенство на значение напряжения и получим формулу для электроемкости параллельно соединенных конденсаторов.

$C = C_1 + C_2 + … + C_n$

{"questions":[{"content":"Напряжение на концах участка цепи с параллельно соединенными конденсаторами равно[[choice-54]]","widgets":{"choice-54":{"type":"choice","options":["напряжению между обкладками любого из конденсаторов","сумме напряжений между обкладками всех конденсаторов","напряжению на полюсах источника тока"],"answer":[0]}}}]}

Первый конденсатор — лейденская банка

Лейденская банка официально является первым конденсатором. Изобретение ее относится к 1745 году. Существует множество версий о том, кто же именно должен считаться изобретателем этого прибора, но официально авторство принадлежит Питеру ван Мушенбруку и его студенту Андреасу Кунэусу.

В ранней версии лейденская банка была на часть заполнена водой, которая выступала в роли обкладки (рисунок 17). Второй обкладкой являлась рука, держащая банку. После зарядки этого приспособления Андреас Кунэус испытал сильный удар током, коснувшись до верха металлического стержня.

Более поздняя и более распространенная версия этого незамысловатого прибора представляет собой сосуд из стекла с широким горлом, снаружи покрытый листом из фольги (рисунок 18). Фольга также находится и внутри банки. Через пробку в этот сосуд вставляется металлический стержень. Он должен касаться фольги внутри банки.

Таким образом, фольга внутри и фольга снаружи становятся своеобразными обкладками. При подключении к источнику тока на них накапливается электрический заряд.

Внимание! Лейденская банка не является безопасным инструментом в электротехнике! Разряд такого конденсатора может оказаться смертельным или привести к серьезным физическим повреждениям.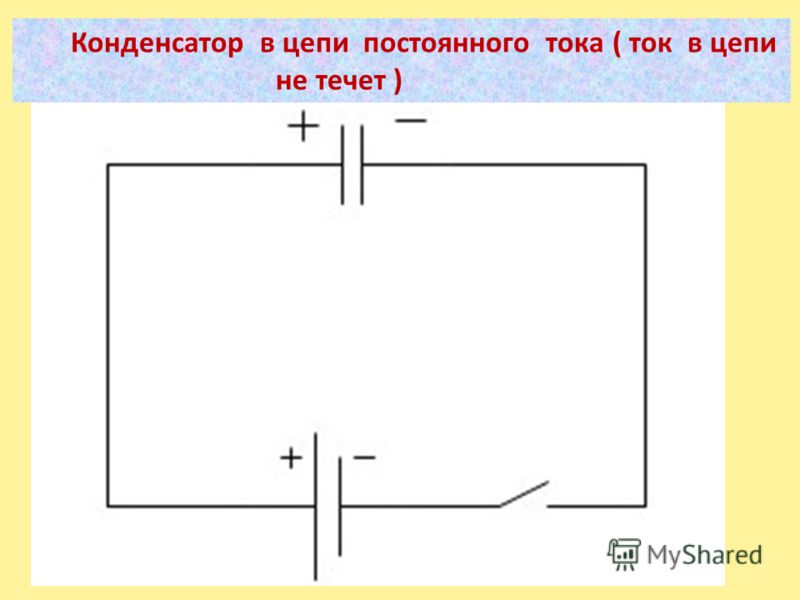 Будьте аккуратны при использовании данного прибора: не следует пытаться разрядить лейденскую банку, взявшись за нее голыми руками.

{"questions":[{"content":"У лейденской банки, изображенной на рисунке 18, обкладками являются[[choice-57]]","widgets":{"choice-57":{"type":"choice","options":["слой фольги снаружи и слой фольги внутри банки","металлический стержень и слой фольги снаружи банки","Пробка и стеклянный сосуд"],"answer":[0]}}}]}

Как изготовить лейденскую банку своими руками? Возьмите пластиковую банку с крышкой (из-под кофе, витаминов). Внешнюю сторону банки на $\frac{2}{3}$ обклейте фольгой. Далее или налейте в банку соленую воду, или обклейте изнутри фольгой. Затем закройте крышку и проткните ее достаточно длинным гвоздем, чтобы он касался внутренней обкладки (воды или фольги). После зарядки такая банка представляет собой заряженный конденсатор.

Упражнения

Упражнение №1

Пластины плоского конденсатора подсоединяют к источнику напряжения в $220 \space В$. 6 \space В$.

Тест, 11 класс. Конденсатор в цепи переменного тока. Вариант 2

Курсы для аттестации учителей от 600 ₽. Документы об окончании по почте БЕСПЛАТНО…

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Состоит из 6 тестовых вопросов. Время выполнения — 4 минут.

Вопрос 1

В электрической цепи, содержащей конденсатор, переменный ток существовать

Варианты ответов

не может, так как между обкладками конденсатора находится диэлектрик
может, так как это или ток заряда, или ток разряда конденсатора
не может, так как конденсатор вообще не проводит электрический ток
может, так как конденсатор — проводник электрического заряда

Вопрос 2

Электрическая цепь содержит конденсатор, к которому подключен источник переменного напряжения. Сила тока в этой цепи становится максимальной, когда конденсатор …

Варианты ответов

начинает заряжаться (напряжение на конденсаторе равно нулю)
начинает разряжаться (напряжение на конденсаторе максимально)
заряжается в течение длительного времени
полностью разряжен

Вопрос 3

Конденсатор электроемкостью С включили в цепь переменного тока (см. рисунок). Если заменить его конденсатором электроемкостью 2С, то при неизменных амплитудном значении напряжения и частоте переменного тока амплитудное значение силы тока …

Варианты ответов

увеличится в 2 раза
увеличится в 4 раза
уменьшится в 2 раза
уменьшится в 4 раза

Вопрос 4

Если электроемкость конденсатора уменьшить в 9 раз, то его емкостное сопротивление …

Варианты ответов

увеличится в 3 раза
увеличится в 9 раз
уменьшится в 3 раза
уменьшится в 9 раз

Вопрос 5

Какой из графиков, изображенных на рисунке, соответствует графику зависимости емкостного сопротивления от циклической частоты переменного тока $\omega$?

Варианты ответов

Вопрос 6

Емкостное сопротивление конденсатора X_c, включенного в цепь переменного тока, и действующие значения напряжения U и силы тока I связаны математическим выражением . ..

Варианты ответов

U = I$/$X_C
U = I$\ast$X²_C
U = I$\ast$X_C
U = I$/$X²_C

Пройти тест

Сохранить у себя:

Лабораторная работа 4. Заряд и разряд конденсатора

Введение

Конденсаторы — это устройства, которые могут накапливать электрический заряд и энергию. Конденсаторы имеют несколько применений, например, фильтры в источниках питания постоянного тока и аккумуляторы энергии для импульсных лазеров.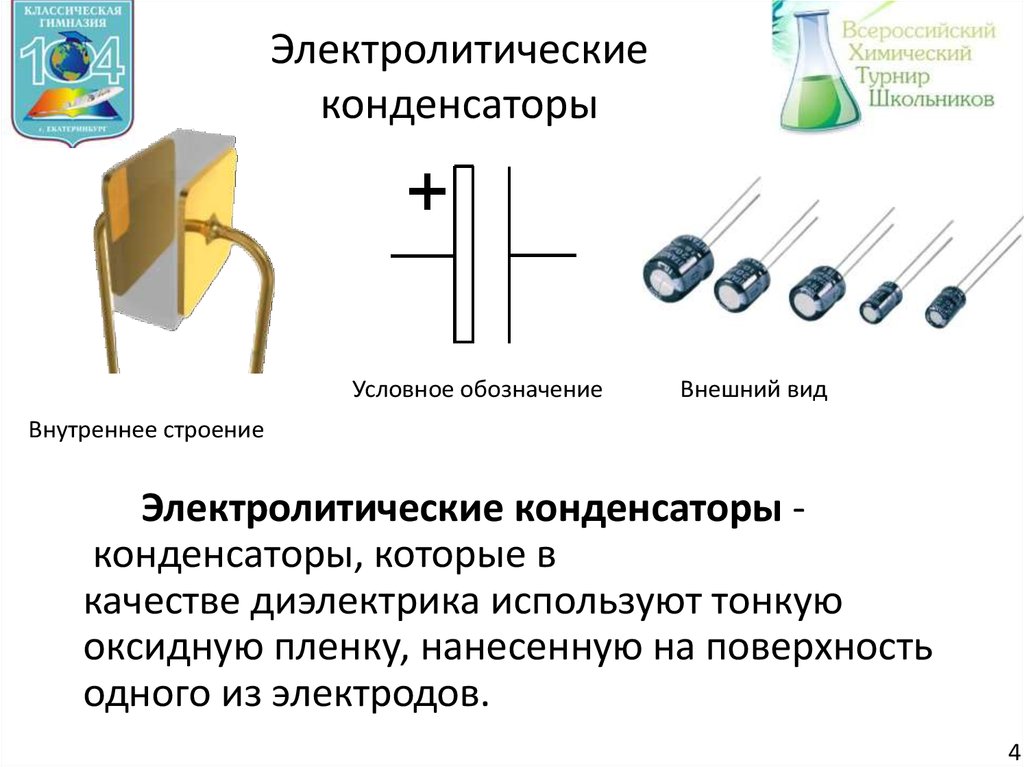 Конденсаторы пропускают переменный ток, но не пропускают постоянный ток, поэтому они используются для блокировки постоянной составляющей сигнала, чтобы можно было измерить переменную составляющую. Физика плазмы использует способность конденсаторов накапливать энергию. В физике плазмы часто требуются короткие импульсы энергии при чрезвычайно высоких напряжениях и токах. Конденсатор можно медленно заряжать до необходимого напряжения, а затем быстро разряжать, чтобы обеспечить необходимую энергию. Можно даже зарядить несколько конденсаторов до определенного напряжения, а затем разрядить их таким образом, чтобы получить из системы большее напряжение (но не больше энергии), чем было введено. В этом эксперименте 9Схема 0005 RC , которая является одной из самых простых схем, использующих конденсатор. Вы изучите эту схему и способы изменения ее эффективной емкости путем последовательного и параллельного соединения конденсаторов.

Обсуждение принципов

Конденсатор состоит из двух проводников, разделенных небольшим расстоянием.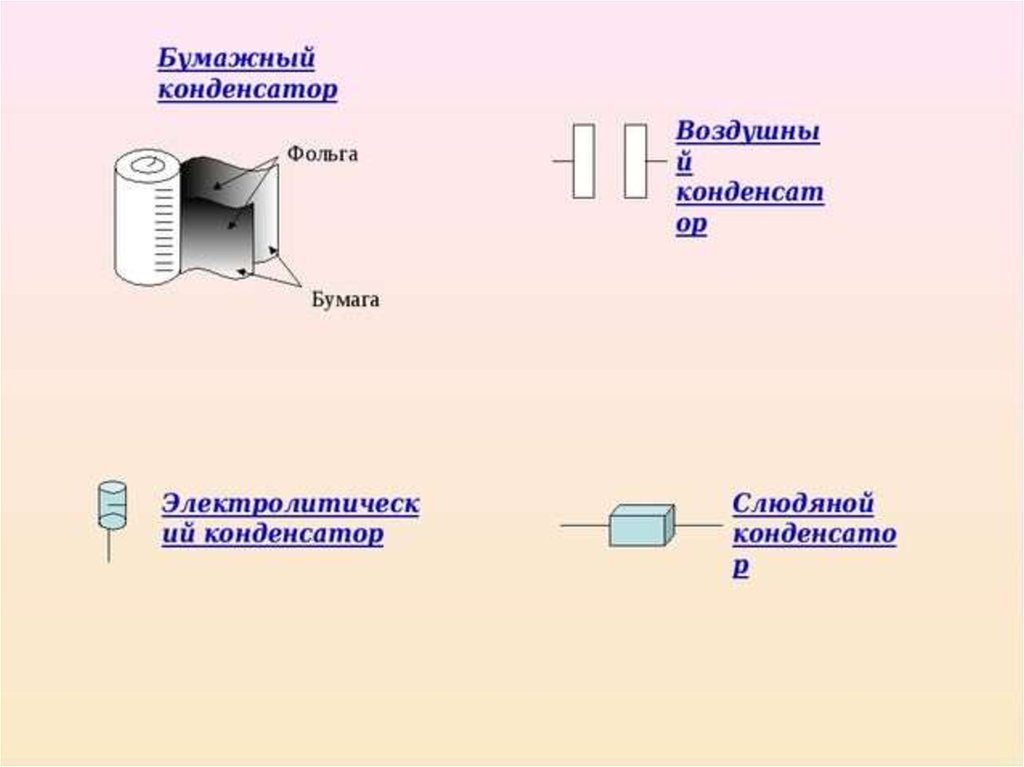 При подключении проводников к зарядному устройству (например, аккумулятору) заряд передается от одного проводника к другому до тех пор, пока разность потенциалов между проводниками из-за их одинакового, но противоположного заряда не станет равной разности потенциалов между выводами зарядного устройства. Количество заряда, накопленного на любом проводнике, прямо пропорционально напряжению, а постоянная пропорциональности известна как емкость . Это записывается алгебраически как

( 1 )

Q = CΔV.

Заряд Кл измеряется в единицах кулонов (Кл), напряжение

ΔV

в вольт (В), а емкость Кл в единицах фарад (Ф). Конденсаторы являются физическими устройствами; емкость это свойство устройств.

Зарядка и разрядка

В простой RC-цепи резистор и конденсатор соединены последовательно с батареей и выключателем. См. рис. 1.

Рисунок 1 : Простая RC-цепочка

Когда переключатель находится в положении 1, как показано на рис. 1 (а), заряд на проводниках через некоторое время достигает максимального значения. Когда переключатель переведен в положение 2, как на рис. 1(b), батарея больше не является частью цепи и, следовательно, заряд конденсатора не может быть восполнен. В результате конденсатор разряжается через резистор. Если мы хотим исследовать зарядку и разрядку конденсатора, нас интересует, что происходит сразу после перевода переключателя в положение 1 или положение 2, а не последующее поведение схемы в устойчивом состоянии. Для схемы, показанной на рис. 1(а), петлевое уравнение Кирхгофа можно записать в виде

( 2 )

ΔV — — R = 0.

Решение уравнения

ΔV − − R = 0,

равно

( 3 )

Q = Q _f

1 − e ^{(−t / RC)}

где

Q _f

представляет собой окончательный заряд конденсатора, который накапливается за бесконечное время, R — сопротивление цепи, а C — емкость конденсатора. Из этого выражения видно, что в процессе зарядки заряд нарастает экспоненциально. См. рис. 2(а). Когда переключатель переводится в положение 2, для схемы, показанной на рис. 1(b), уравнение контура Кирхгофа теперь имеет вид

(4)

− R = 0.

Решение уравнения

— R = 0.

есть

( 5 )

Q = Q ₀ e ^{(−t / RC)}

где

Q ₀

представляет собой начальный заряд конденсатора в начале разряда, т. е. при

t = 0. разряжается, и что для полной разрядки требуется бесконечное количество времени. См. рис. 2(б).

Рисунок 2 : Графики изменения во времени

Постоянная времени

Продукт

(имеющий единицы времени) имеет особое значение; это называется постоянной времени цепи.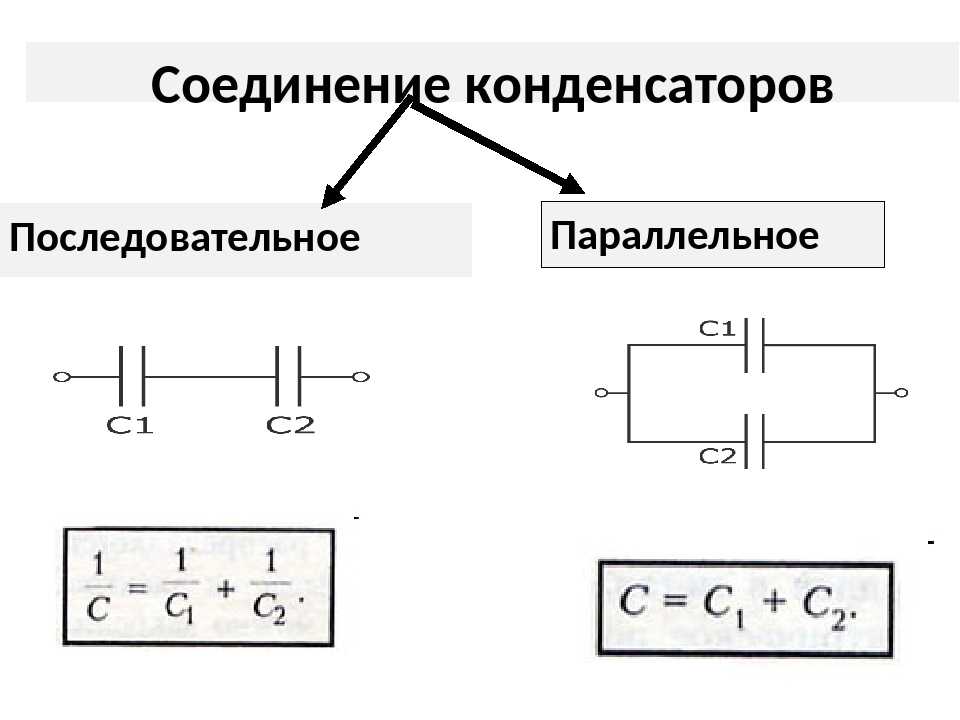 Постоянная времени — это количество времени, необходимое для того, чтобы заряд зарядного конденсатора увеличился до 63% от его конечного значения. Другими словами, когда

t = RC,

( 6 )

Q = Q _f

1 − e ⁻¹

9 а также

( 7 )

1 − e ⁻¹ = 0,632.

Другой способ описать постоянную времени — это количество секунд, необходимое для того, чтобы заряд разряжающегося конденсатора упал до 36,8%

(e ⁻¹ = 0,368)

от его начального значения. Мы можем использовать определение

(I = dQ/dt)

тока через резистор и

Q = Q _F

1 — E ^{(−T / RC)}

Q = Q ₀ e ^{(−t / RC)}

, чтобы получить выражение для тока в процессах зарядки и разрядки.

( 8 )

зарядка: I = +I ₀ e ^-t/RC

( 9 )

разрядка: I = -I ₀ e ^-t/RC

где

I ₀ =

зарядка: I = +I ₀ e ^−t/RC

разряд: I = −I ₀ e ^−t/RC

– максимальный ток в цепи в момент времени t = 0. Тогда разность потенциалов на резисторе будет определяться следующим образом.

( 10 )

charging: ΔV = + ΔV _f e ^−t/RC

( 11 )

discharging: ΔV = − ΔV ₀ e ^−t/RC

Обратите внимание, что в процессе разрядки ток будет течь через резистор в противоположном направлении. Отсюда I и

ΔV

в уравнении

разрядка: I = -I ₀ e ^-t/RC

при разрядке: ΔV = − ΔV ₀ e ^−t/RC

отрицательны. Это напряжение как функция времени показано на рис. 3.

Рисунок 3 : Напряжение на резисторе как функция времени

Полезно описывать зарядку и разрядку с точки зрения разности потенциалов между проводниками (т. Е. «Напряжения на конденсаторе»), поскольку напряжение на конденсаторе можно измерить непосредственно в лаборатории. Используя соотношение

Q = C ΔV,

Q = Q _F

1 — E ^{(−T / RC)}

Q = Q ₀ e ^{(−t / RC)}

, которые описывают зарядку и разрядку конденсатора, можно переписать в терминах напряжения. Просто разделите оба уравнения на

, и соотношение станет следующим.

( 12 )

charging: ΔV = ΔV _f

1 − e ^(−t/RC)

( 13 )

discharging : ΔV = ΔV ₀ e ^(−t/RC)

Обратите внимание, что эти два уравнения похожи по форме на уравнение

Q = Q _f

1 − e ^{(−t / RC)}

Q = Q ₀ e ^{(−t / RC)}

. График зависимости напряжения на конденсаторе от времени показан на рис. 4 ниже.

Рисунок 4 : Напряжение на конденсаторе как функция времени

Путем перестановки

зарядка: ΔV = ΔV _f

1 − e ^(−t/RC)

получаем

(14)

ΔV _F — ΔV

ΔV _F

^(–T/RC)

Возьмите натуральный логарифм (ln) обеих частей этого выражения и умножьте на –1, чтобы получить

( 15 )

−ln

ΔV _f − ΔV

ΔV _f

4 4 =.

График зависимости
−ln((ΔV _f − ΔV)/ΔV _f )
от времени даст прямолинейный график с наклоном 1/ RC . Точно так же для процесса разрядки
экв. 13
разрядка: ΔV = ΔV ₀ e ^(−t/RC)
можно переписать, чтобы получить
( 16 )
= e ^(−t/RC) .
Возьмите натуральный логарифм (ln) обеих частей этого выражения и умножьте на –1, чтобы получить
( 17 )
−ln

9 90.

График зависимости

−ln(ΔV)/ΔV ₀ )

от времени даст прямую линию с наклоном 1/9. 0005 RC .

Использование прямоугольной волны для имитации роли переключателя

В этом эксперименте вместо переключателя мы будем использовать генератор сигналов, который может генерировать периодические волны различной формы, такие как синусоида, треугольная волна и прямоугольная волна. Также можно регулировать как частоты, так и амплитуды волновых форм. Здесь мы будем использовать генератор сигналов для создания изменяющегося во времени напряжения прямоугольной формы на конденсаторе, подобного показанному на рис. 5.

Рисунок 5 : Прямоугольная волна с периодом Τ

Выходное напряжение генератора сигналов изменяется взад и вперед от постоянного положительного значения до постоянного нуля вольт через равные промежутки времени t . Время

T = 2t

— это период прямоугольной волны. В течение первой половины цикла, когда напряжение положительное, это похоже на то, что переключатель находится в положении 1. Во время второй половины цикла, когда напряжение равно нулю, это то же самое, что и переключатель в положении 2. Таким образом, прямоугольная волна, представляющая собой постоянное напряжение, которое периодически включается и выключается, служит одновременно и батареей, и переключателем в схеме, показанной на рис. Генератор сигналов позволяет выполнять это переключение многократно, и можно оптимизировать сбор данных, регулируя частоту повторения. Эта частота будет зависеть от постоянной времени RC-цепи. Когда время t больше, чем постоянная времени τ RC-цепи, у конденсатора будет достаточно времени для зарядки и разрядки, а напряжение на конденсаторе будет таким, как показано на рис. 4.

Объектив

В этом эксперименте будет использоваться (эмулируемый компьютером) осциллограф для контроля разности потенциалов и, таким образом, косвенно, заряда конденсатора. Измерения напряжения будут использоваться двумя разными способами для вычисления постоянной времени цепи. Наконец, конденсаторы будут соединены параллельно, чтобы проверить их эквивалентную емкость цепи.

Оборудование

печатная плата ПАСКО
Сигнальный интерфейс с выходной мощностью
Соединительные провода
Программное обеспечение Capstone

Процедура

Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.

Установка RC-цепи

Печатная плата RLC, которую вы будете использовать, состоит из трех резисторов и двух конденсаторов среди других элементов. См. рис. 6 ниже. Теоретически у вас могут быть разные комбинации резисторов и конденсаторов. В этом эксперименте вы будете использовать резисторы 33 Ом и 100 Ом и два конденсатора.

Рисунок 6 : Печатная плата RLC

Подключите крайнюю правую выходную клемму сигнального интерфейса к резистору 33 Ом в точке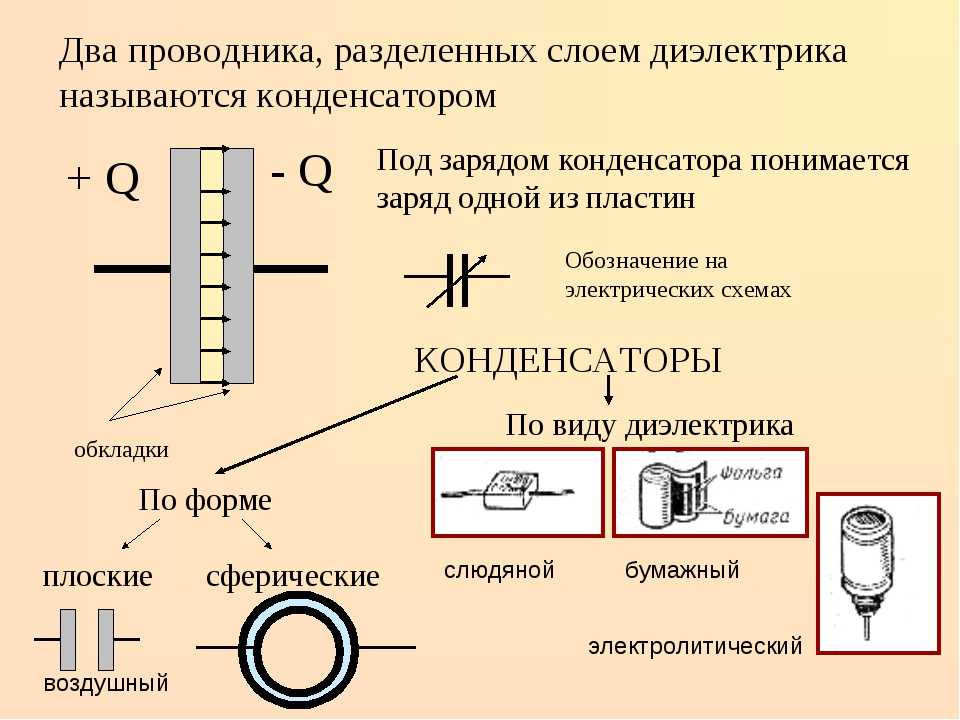 2.

Для обхода катушки индуктивности подключите провод от точки 8 к точке 9.

Подключите точку 6 ко второй выходной клемме сигнального интерфейса, чтобы замкнуть цепь.

Подключите пробник напряжения к аналоговому каналу А.

Чтобы измерить напряжение на конденсаторе, подключите черный провод пробника напряжения к точке 6, а красный провод к точке 9.. Убедитесь, что земля интерфейса (вывод «–») подключена к той же стороне конденсатора, что и земля генератора сигналов (выходная мощность). Подключение вашей схемы должно выглядеть так, как показано на рис. 7.

Рисунок 7 : Принципиальная схема

Контрольная точка 1:
Попросите вашего ТА проверить соединения вашей цепи.

Процедура A: постоянная времени цепи

В этом эксперименте мы будем использовать компьютер для эмуляции осциллографа.

Откройте файл Capstone, связанный с этой лабораторией. Отображается экран, аналогичный рис. 8.

Рисунок 8 : Экран открытия файла Capstone

Настройте генератор сигналов на создание положительной прямоугольной волны, выбрав положительную прямоугольную волну в окне генератора сигналов, как показано на рис. 9 ниже.

Рисунок 9 : Окно генератора сигналов

Если он еще не установлен при открытии файла Capstone, настройте генератор сигналов на создание прямоугольной волны амплитудой 5 В с частотой 20 Гц и установите смещение напряжения на 5 В.

Включите генератор сигналов, нажав ON в окне генератора сигналов.

Для мониторинга сигнала нажмите кнопку START в главном окне. Будет необходимо отрегулировать шкалы времени и напряжения, чтобы получить кривую сигнала, подобную той, что показана на рис. 10. Это позволит вам наблюдать, как напряжение на конденсаторе изменяется в зависимости от времени. Для этого установите курсор на любое значение по оси, которую вы хотите увеличить, и перемещайте курсор влево-вправо или вверх-вниз по мере необходимости. При правильном масштабировании на графике будет отображаться только одна длина волны, как на графике на рис. 10.

Рисунок 10 : Трассировка сигнала

Если в любой момент вы захотите удалить записанный набор данных, нажмите кнопку Удалить последний прогон под графиком.

Выберите кнопку Показать координаты из кнопок над графиком. См. рис. 11.

Рисунок 11 : Показать координаты

Когда отображение координат активно, показания напряжения и времени отображаются везде, где вы их перетаскиваете, как на рис. 11. Используя этот инструмент, определите и запишите время начала (т. е. когда кривая началась вверх от 0 вольт) на рабочем листе.

Рассчитайте 63,2% от максимального напряжения,

ΔV _f ,

(которое должно быть 5 В), настройку по амплитуде генератора сигналов. Используя Показать координаты , определите и запишите время начала (т. е. когда трасса начинается вверх от 0 вольт) на листе.

По этим двум значениям времени определите и запишите время, необходимое сигналу для перехода от Δ В = от 0 до Δ В = 0,632

ΔV _f .

Это экспериментальное значение для RC .

На рабочем листе заполните принятые значения сопротивления и емкости, которые напечатаны на печатной плате.

Вычислите экспериментальное значение емкости, используя экспериментальное значение для RC и принятое значение 9.0005 Р . Запишите это в рабочий лист.

Вычислите процентную ошибку, используя два значения емкости. См. Приложение Б.

КПП 2:
Попросите вашего ТА проверить ваши данные и расчеты, прежде чем продолжить.

Процедура B: Расчет емкости графическими методами

Запишите максимальное напряжение в рабочий лист.

По записанным данным найдите моменты времени, когда Δ В = 1, 2, 3 и 4 вольт на восходящей части кривой с помощью интеллектуального инструмента. Запишите эту информацию в таблицу данных 1 на рабочем листе. Примечание . Возможно, вам придется значительно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента.

Выполните необходимые расчеты, чтобы заполнить таблицу данных 1.

Используя Excel, постройте график

−ln((ΔV _f − ΔV) / ΔV _f )

в зависимости от времени. См. Приложение G.

Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе. См. Приложение Н.

По значению наклона определите постоянную времени и емкость. Запишите эти значения в рабочий лист.

Вычислите процентную ошибку между этим значением емкости и принятым значением.

КПП 3:
Попросите вашего ТА проверить ваши данные, график и расчеты, прежде чем продолжить.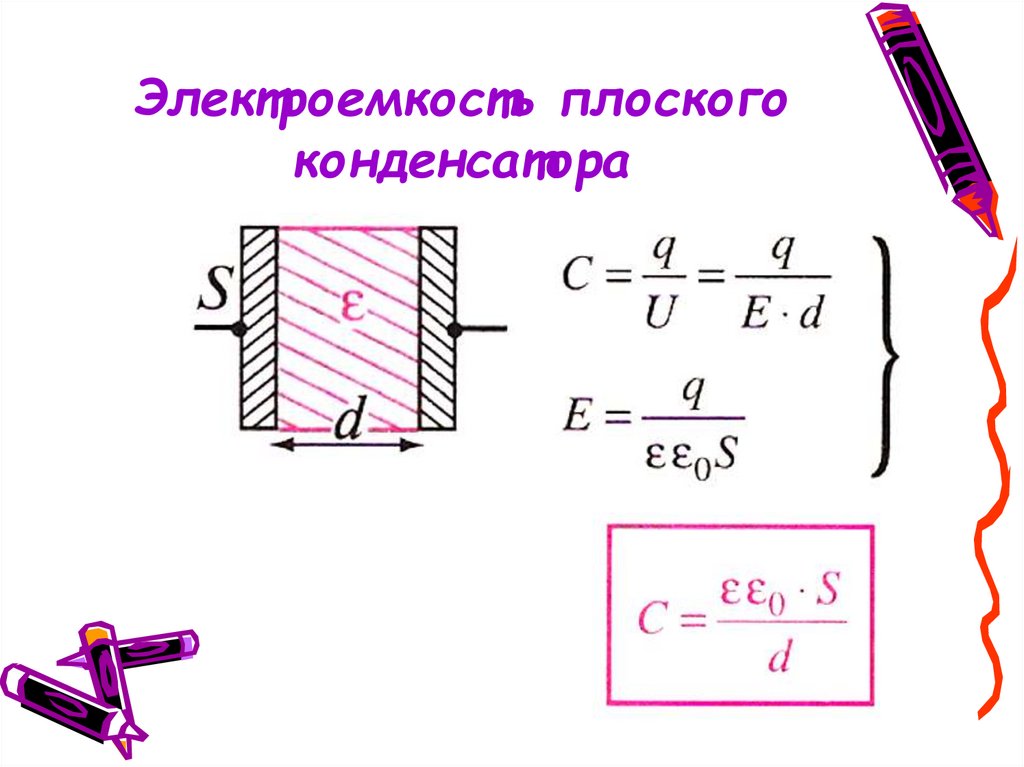

Процедура C: Измерение эффективной емкости

Емкость складывается напрямую, когда конденсаторы соединены параллельно, и наоборот, при последовательном соединении. Это противоречит правилу для резисторов. Для конденсаторов, включенных параллельно, эффективная емкость определяется выражением

( 18 )

С _эфф = С ₁ + С ₂ + С ₃ + . . .

а для последовательно соединенных конденсаторов эффективная емкость равна

( 19 )

= + + + . . .

Подсоедините второй конденсатор (330 мк Ф) параллельно конденсатору, используемому в процедуре А, подключив провод от точки 6 к точке 7.

Переключите резистор на резистор 10 Ом, переместив соединение из точки 2 в точку 1.

Запишите другой набор данных, нажав START в главном окне. После того, как вы записали второй набор данных, вы можете захотеть отобразить только эти данные на графике и удалить набор данных 1. Для этого удалите первый запуск (см. примечание к шагу 10). На графическом дисплее вы будете видеть только одну длину волны.

В этой части эксперимента вы будете рассматривать разгрузочную часть кривой. Теперь начальное напряжение

ΔV ₀

будет самым высоким значением пика до того, как график начнет падать. Запишите это значение в рабочий лист.

По записанным данным найдите моменты времени, когда Δ В = 1, 2, 3 и 4 вольта на падающей части кривой с помощью интеллектуального инструмента. ( Примечание : вам может потребоваться сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента). Запишите эту информацию в таблицу данных 2 на рабочем листе.

Выполните необходимые расчеты, чтобы заполнить таблицу данных 2.

Используя Excel, постройте график зависимости

−ln(ΔV) / ΔV ₀ )

от времени.

Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе.

По значению наклона определите постоянную времени и запишите это значение в рабочий лист.

Вычислите

C _eff ,

эффективную емкость параллельной комбинации, используя принятое значение для R .

Сравните это экспериментальное значение с тем, что вы получили из уравнения

С _эфф = С ₁ + С ₂ + С ₃ + . . .

и принятые значения емкости путем вычисления процентной ошибки между двумя значениями.

КПП 4:
Попросите вашего ТА проверить ваши данные и расчеты, прежде чем продолжить.

Конденсатор — обучение энергетике

Меню навигации

ИСТОЧНИКИ ЭНЕРГИИ

ИСПОЛЬЗОВАНИЕ ЭНЕРГИИ

ЭНЕРГЕТИЧЕСКОЕ ВОЗДЕЙСТВИЕ

Поиск

Рис. 1. Схема конденсатора, включающего две параллельные пластины с площадью поверхности A и расстоянием между ними d. Хотя не все конденсаторы имеют такую форму, их часто считают таковыми, поскольку это самая простая геометрия.

Рис. 2. Анимация из имитации PhET батареи, заряжающей конденсатор до тех пор, пока ток не перестанет течь по цепи.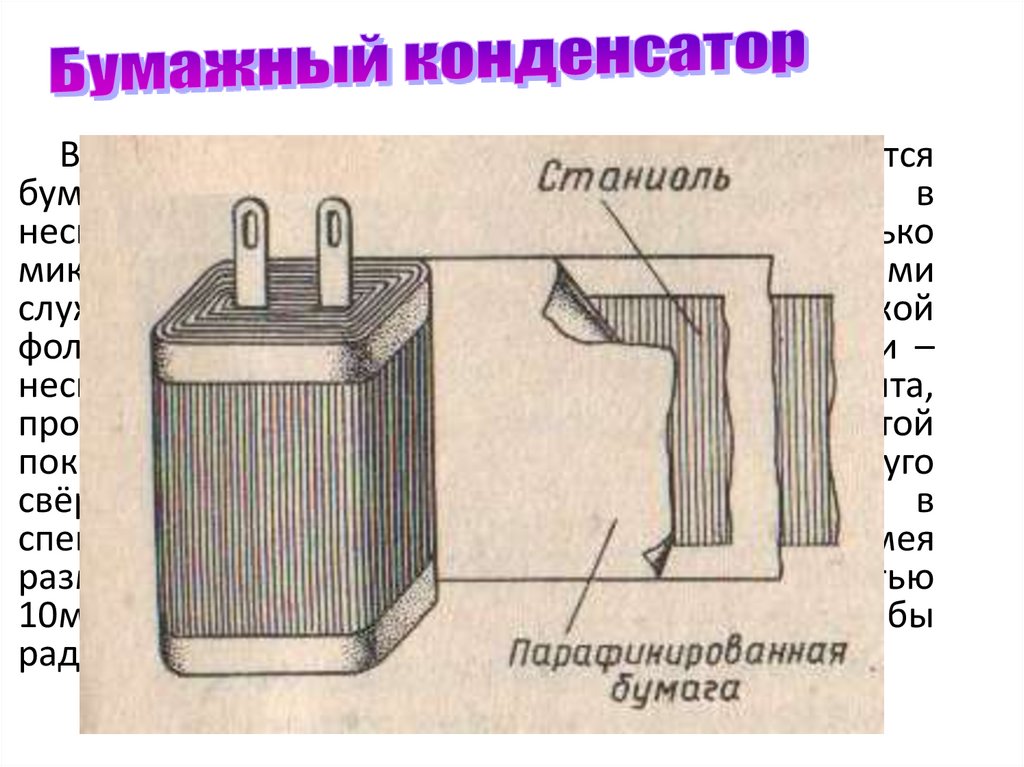 ^[1]

Конденсатор — это электронное устройство, накапливающее заряд и энергию. Конденсаторы могут отдавать энергию намного быстрее, чем батареи, что приводит к гораздо более высокой плотности мощности, чем батареи с таким же количеством энергии. Исследования конденсаторов продолжаются, чтобы выяснить, можно ли их использовать для хранения электроэнергии для электрической сети. В то время как конденсаторы — это старая технология, суперконденсаторы — это новый поворот в этой технологии.

Конденсаторы — это простые устройства, состоящие из двух проводников с одинаковыми, но противоположными зарядами. Простой конденсатор с плоскими пластинами состоит из двух металлических пластин одинакового размера, известных как электроды, разделенных изолятором, известным как диэлектрик, которые удерживаются параллельно друг другу. Затем конденсатор включается в электрическую цепь. В простой цепи постоянного тока каждая пластина конденсатора со временем становится противоположно заряженной из-за прохождения электрического тока по цепи. Аккумулятор направляет заряд в одном направлении, так что одна пластина становится положительно заряженной, а другая — отрицательной. Это создает электрическое поле из-за накопления одинаковых и противоположных зарядов, что приводит к разности потенциалов или напряжению между пластинами. Поскольку емкость пластин постоянна, напряжение между пластинами пропорционально увеличивается. По мере увеличения заряда на каждой пластине напряжение между пластинами равняется напряжению батареи, после чего ток больше не будет течь по цепи. ^[2] Этот эффект зарядки и разрядки можно увидеть на рис. 2. Ток может возобновиться, если открыть альтернативный путь, чтобы конденсаторы могли разряжаться самостоятельно, или с помощью переменного тока, чтобы конденсатор периодически заряжался и разряжался.

Важным параметром конденсатора является емкость, мера способности объекта накапливать заряд. Есть два основных способа расчета емкости, используя либо физическую площадь пластин, либо напряжение, приложенное к пластинам.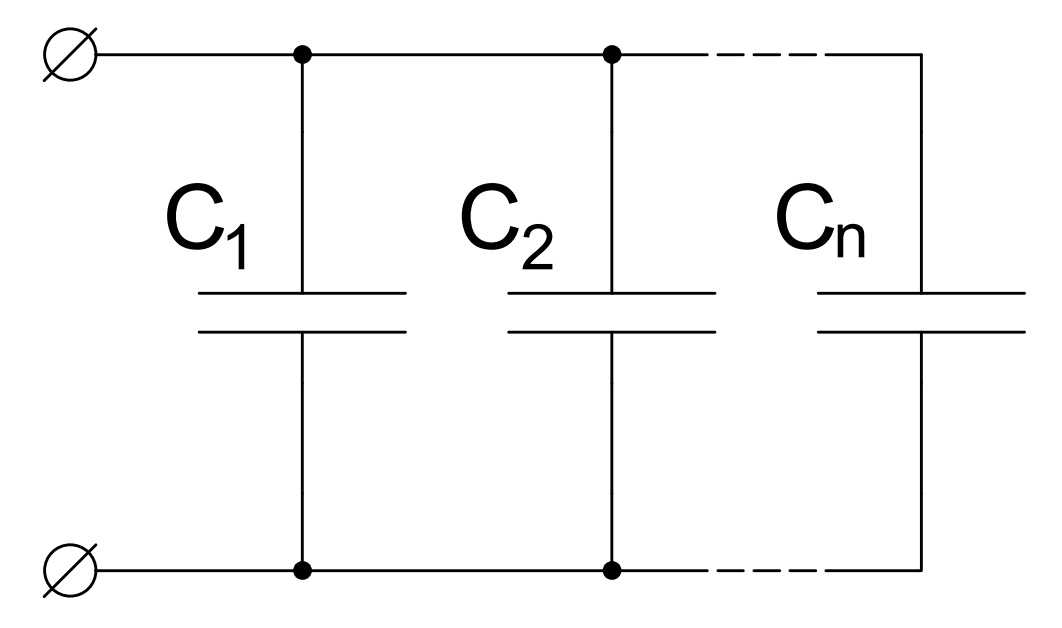 92} {2}[/math]

[math]\Delta V[/math] — напряжение между пластинами, измеренное в вольтах (В)
[math]C[/math] — емкость конденсатора, измеренная в фарадах (Ф)
[math]E[/math] энергия, запасенная в конденсаторе, измеряемая в джоулях (Дж)

В качестве альтернативы в конденсатор можно добавить диэлектрик. Диэлектрик представляет собой изолятор, помещенный между электродами. Это увеличивает емкость конденсатора без необходимости изменения его размеров. Это позволяет конденсатору хранить больше энергии, оставаясь при этом небольшим. Степень увеличения зависит от материала, используемого для диэлектрика. ^[3]

Использование

Конденсаторы не обладают такой высокой плотностью энергии, как батареи, а это означает, что конденсатор не может хранить столько энергии, сколько батарея сравнимого размера. Тем не менее, более высокая мощность конденсаторов означает, что они хороши для приложений, требующих хранения небольшого количества энергии, а затем очень быстрого ее высвобождения. 9Гоночные автомобили 0994 Le Mans Prototype используют конденсаторы для питания электродвигателей передних колес. Эти конденсаторы заряжаются за счет рекуперативного торможения и обеспечивают полный привод и дополнительную мощность при выходе из поворотов. ^[4]

Конденсаторы также используются во многих электронных устройствах, для которых требуется батарея. Этот конденсатор накапливает энергию, чтобы предотвратить потерю памяти при замене батареи. Распространенный (хотя и не обязательно широко известный) пример — зарядка вспышки фотокамеры. Вот почему нельзя сделать два снимка со вспышкой в быстрой последовательности; конденсатор должен накапливать энергию от батареи. ^[5]

Кроме того, конденсаторы играют ключевую роль во многих практических цепях, прежде всего в качестве стабилизаторов тока и компонентов, помогающих преобразовать переменный ток в постоянный в адаптерах переменного тока. Их можно использовать таким образом из-за того, что конденсаторы устойчивы к внезапным изменениям напряжения, а это означает, что они могут действовать как буфер для хранения и отвода электроэнергии для поддержания стабильного выходного тока. ^[6] Таким образом, конденсатор способен стабилизировать переменный ток благодаря своей способности удерживать и отдавать электрическую энергию в разное время.

Поскольку конденсаторы хранят энергию в электрических полях, некоторые исследователи работают над созданием суперконденсаторов, чтобы помочь с хранением энергии. Это может оказаться полезным при транспортировке энергии или для хранения и высвобождения энергии из непостоянных источников, таких как энергия ветра и солнца.

Моделирование Phet

Университет Колорадо любезно разрешил нам использовать следующее моделирование Phet. Исследуйте эту симуляцию, чтобы увидеть, как потенциальная энергия гравитации и потенциальная энергия пружины перемещаются вперед и назад и создают изменяющееся количество кинетической энергии (подсказка: нажмите показать энергию до подвешивания массы):

Ссылки

↑ Университет Колорадо. (25 апреля 2015 г.). Набор для сборки схем [Онлайн]. Доступно: http://phet.colorado.edu/sims/circuit-construction-kit/circuit-construction-kit-ac_en.jnlp
↑ Гиперфизика. (25 апреля 2015 г.). Конденсаторы [Онлайн]. Доступно: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/capac.html
↑ Р. Д. Найт, «Потенциал и поле», в Физика для ученых и инженеров: стратегический подход, , 2-е изд. Сан-Франциско: Пирсон Аддисон-Уэсли, 2008 г., гл. 30, с. 5, стр. 922-932.
↑ «Суперконденсаторы берут верх в Германии», Филип Болл, бюллетень MRS, том 37, выпуск 09, 2012 г., стр. 802–803.
↑ (2014, 27 июня). Как работают вспышки камеры [Онлайн]. Доступно: http://electronics.howstuffworks.com/camera-flash.htm
↑ Искра. (25 апреля 2015 г.). Конденсаторы [Онлайн]. Доступно: https://learn.sparkfun.com/tutorials/capacitors

8.2 Конденсаторы, включенные последовательно и параллельно — University Physics Volume 2

Цели обучения

К концу этого раздела вы сможете:

Объясните, как определить эквивалентную емкость конденсаторов при последовательном и параллельном соединении
Вычислить разность потенциалов на пластинах и заряд на пластинах для конденсатора в сети и определить чистую емкость сети конденсаторов

Несколько конденсаторов можно соединить вместе для использования в различных приложениях. Несколько соединений конденсаторов ведут себя как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Конденсаторы могут быть расположены в двух простых и распространенных типах соединений, известных как , серия и , параллельная , для которых мы можем легко рассчитать общую емкость. Эти две основные комбинации, последовательная и параллельная, также могут использоваться как часть более сложных соединений.

Серийная комбинация конденсаторов

На рис. 8.11 показано последовательное соединение трех конденсаторов, расположенных в ряд внутри цепи. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением с помощью уравнения 8.1. При подключении этой последовательной комбинации к батарее с напряжением В каждый из конденсаторов приобретает одинаковый заряд Q .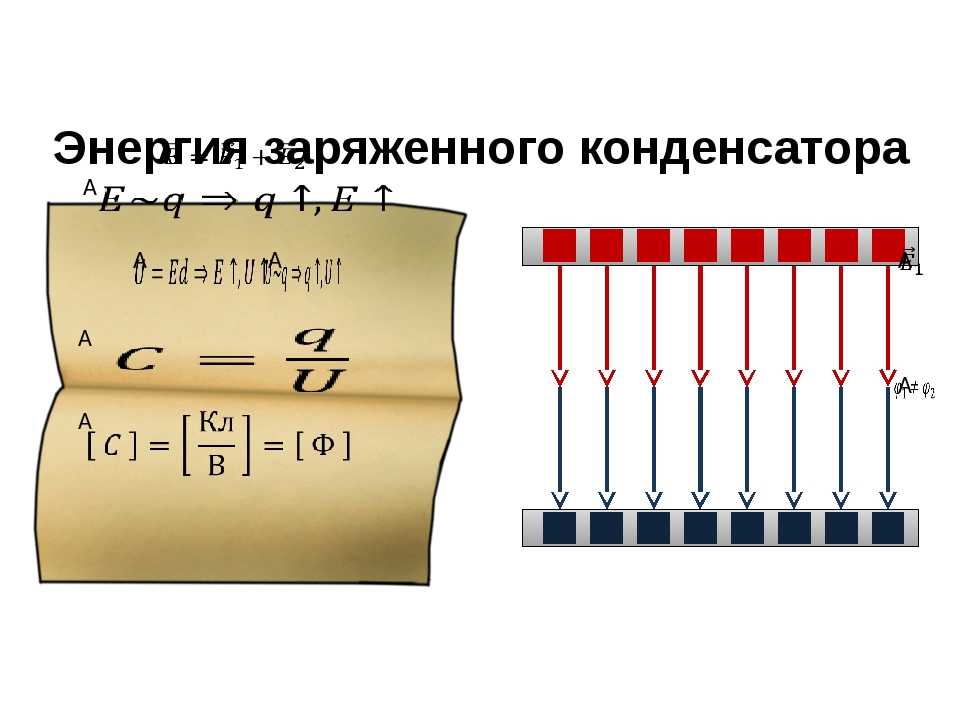 Чтобы объяснить, сначала обратите внимание, что заряд на пластине, подключенной к положительной клемме батареи, равен +Q+Q, а заряд на пластине, подключенной к отрицательной клемме, равен -Q-Q. Затем заряды индуцируются на других пластинах, так что сумма зарядов на всех пластинах и сумма зарядов на любой паре пластин конденсатора равна нулю. Однако падение потенциала V1=Q/C1V1=Q/C1 на одном конденсаторе может отличаться от падения потенциала V2=Q/C2V2=Q/C2 на другом конденсаторе, поскольку, как правило, конденсаторы могут иметь разные емкости. Последовательное соединение двух или трех конденсаторов напоминает один конденсатор с меньшей емкостью. Как правило, любое количество последовательно соединенных конденсаторов эквивалентно одному конденсатору, емкость которого (называемая (эквивалентная емкость Ом) меньше, чем наименьшая из емкостей в последовательной комбинации. Заряд этого эквивалентного конденсатора такой же, как заряд любого конденсатора в последовательном соединении: То есть все конденсаторы последовательного соединения имеют одинаковый заряд . Это происходит из-за сохранения заряда в цепи. Когда заряд Q в последовательной цепи снимается с пластины первого конденсатора (обозначается -Q-Q), он должен быть помещен на пластину второго конденсатора (обозначается +Q), +Q) и так далее.

Рисунок 8.11 а) Три конденсатора соединены последовательно. Величина заряда на каждой пластине Å . (b) Цепь конденсаторов в (а) эквивалентна одному конденсатору, емкость которого меньше, чем у любой из отдельных емкостей в (а), а заряд на его обкладках равен Ом .

Мы можем найти выражение для полной (эквивалентной) емкости, рассматривая напряжения на отдельных конденсаторах. Потенциалы на конденсаторах 1, 2 и 3 равны соответственно V1=Q/C1V1=Q/C1, V2=Q/C2V2=Q/C2 и V3=Q/C3V3=Q/C3. Эти потенциалы должны суммироваться с напряжением батареи, что дает следующий баланс потенциалов:

В=В1+В2+В3.В=В1+В2+В3.

Потенциал В измеряется на эквивалентном конденсаторе, который удерживает заряд Q и имеет эквивалентную емкость CSCS.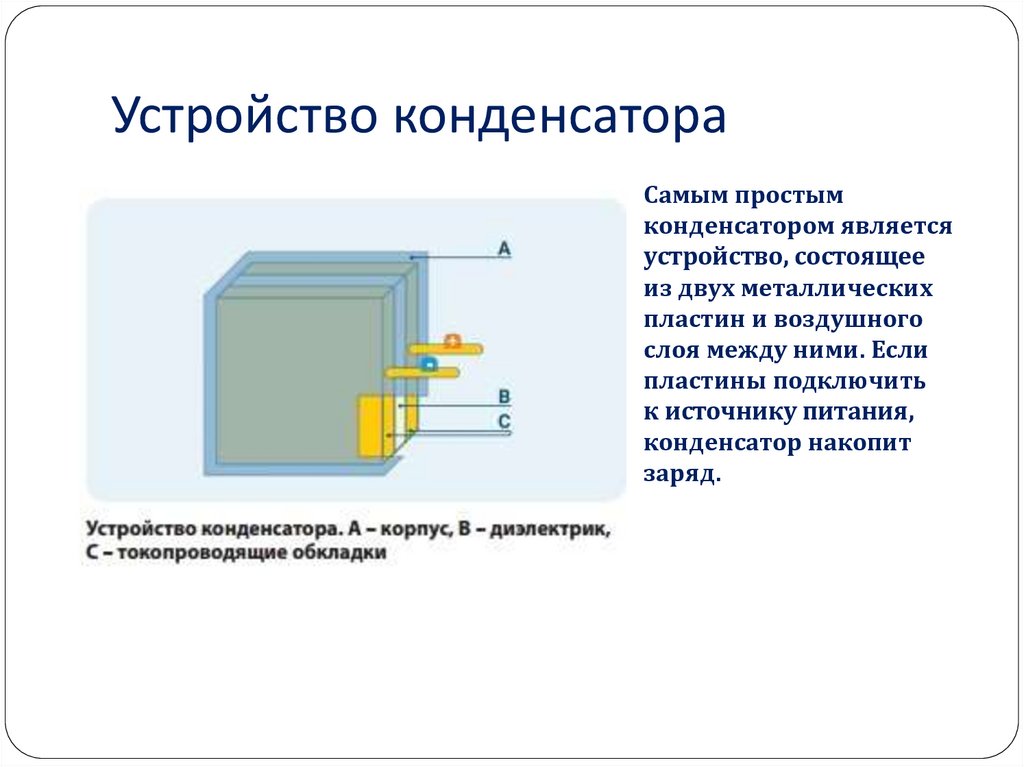 Вводя выражения для V1V1, V2V2 и V3V3, получаем

QCS=QC1+QC2+QC3.QCS=QC1+QC2+QC3.

Отменяя заряд Q , получаем выражение, содержащее эквивалентную емкость CSCS трех последовательно соединенных конденсаторов:

1CS=1C1+1C2+1C3.1CS=1C1+1C2+1C3.

Это выражение можно обобщить для любого количества конденсаторов в последовательной сети.

Комбинация серий

Для последовательно соединенных конденсаторов обратная величина эквивалентной емкости представляет собой сумму обратных величин отдельных емкостей:

1CS=1C1+1C2+1C3+⋯.1CS=1C1+1C2+1C3+⋯.

8,7

Пример 8.4

Эквивалентная емкость последовательной сети

Найдите общую емкость трех последовательно соединенных конденсаторов, если их отдельные емкости равны 1000 мкФ, 1000 мкФ, 5000 мкФ, 5000 мкФ и 8000 мкФ, 8000 мкФ.

Стратегия

Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8.7 с тремя членами.

Раствор

Мы вводим данные емкости в уравнение 8.7:

1CS=1C1+1C2+1C3=11,000 мкФ+15,000 мкФ+18,000 мкF1CS=1,325 мкФ.1CS=1C1+1C2+1C3=11,000 мкФ+15,000 мкФ+18,000 мкФ1CS=1,325 мкФ.

Теперь инвертируем этот результат и получаем CS=мкФ1,325=0,755мкФ.CS=мкФ1,325=0,755мкФ.

Значение

Обратите внимание, что в последовательной сети конденсаторов эквивалентная емкость всегда меньше наименьшей отдельной емкости в сети.

Параллельная комбинация конденсаторов

Параллельная комбинация трех конденсаторов, в которой одна пластина каждого конденсатора подключена к одной стороне цепи, а другая пластина подключена к другой стороне, показана на рис. 8.12 (а). Так как конденсаторы соединены параллельно, все они имеют одинаковое напряжение V на своих обкладках . Однако каждый конденсатор в параллельной сети может хранить различный заряд. Чтобы найти эквивалентную емкость CPCP параллельной сети, заметим, что общий заряд Q , хранящийся в сети, представляет собой сумму всех отдельных зарядов:

Q=Q1+Q2+Q3.Q=Q1+Q2+Q3.

В левой части этого уравнения мы используем соотношение Q=CPVQ=CPV, которое верно для всей сети. В правой части уравнения мы используем соотношения Q1=C1V, Q2=C2V, Q1=C1V, Q2=C2V и Q3=C3VQ3=C3V для трех конденсаторов в сети. Таким образом, мы получаем

CPV=C1V+C2V+C3V.CPV=C1V+C2V+C3V.

Это уравнение в упрощенном виде представляет собой выражение для эквивалентной емкости параллельной сети из трех конденсаторов:

СР=С1+С2+С3. СР=С1+С2+С3.

Это выражение легко обобщается на любое количество конденсаторов, соединенных параллельно в сети.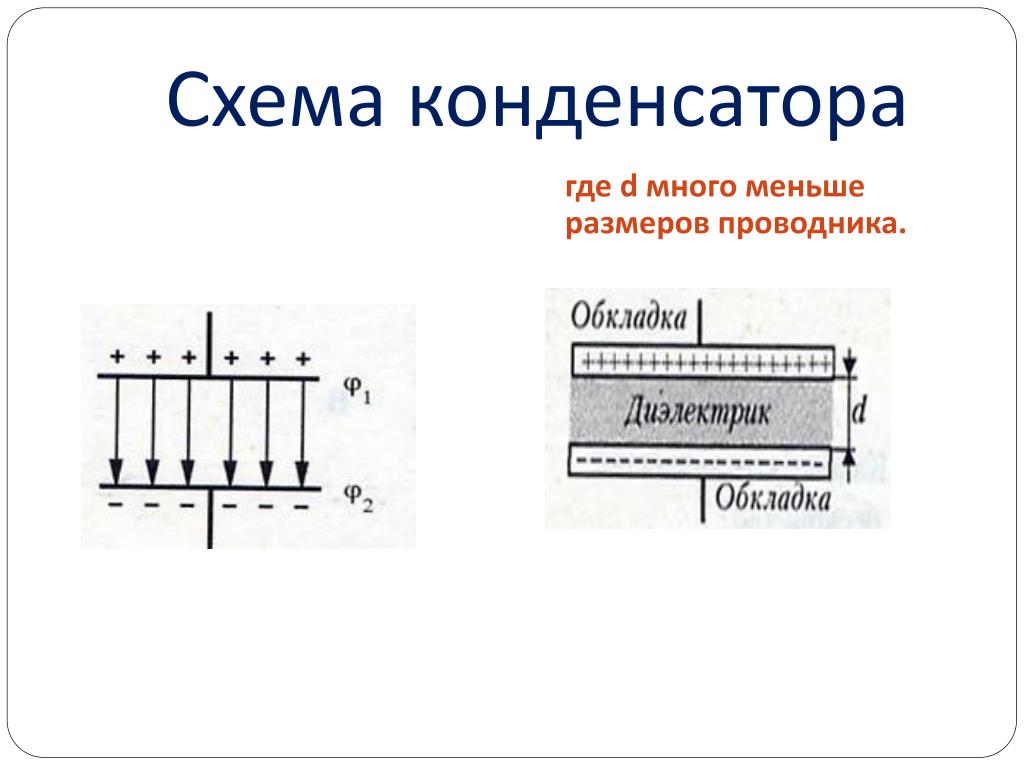

Параллельная комбинация

Для конденсаторов, соединенных параллельно, эквивалентная (чистая) емкость представляет собой сумму всех отдельных емкостей в сети,

CP=C1+C2+C3+⋯.CP=C1+C2+C3+⋯.

8,8

Рисунок 8.12 а) Три конденсатора соединены параллельно. Каждый конденсатор подключен непосредственно к аккумулятору. б) Заряд эквивалентного конденсатора равен сумме зарядов отдельных конденсаторов.

Пример 8,5

Эквивалентная емкость параллельной сети

Найдите общую емкость для трех конденсаторов, соединенных параллельно, учитывая, что их отдельные емкости составляют 1,0 мкФ, 5,0 мкФ и 8,0 мкФ, 1,0 мкФ, 5,0 мкФ и 8,0 мкФ.

Стратегия

Поскольку в этой цепи всего три конденсатора, мы можем найти эквивалентную емкость, используя уравнение 8. 8 с тремя членами.

Раствор

Ввод данных емкостей в уравнение 8.8 дает

CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФCP=14,0 мкФ. CP=C1+C2+C3=1,0 мкФ+5,0 мкФ+8,0 мкФCP=14,0 мкФ.

Значение

Обратите внимание, что в параллельной сети конденсаторов эквивалентная емкость всегда больше, чем любая из отдельных емкостей в сети.

Сети конденсаторов обычно представляют собой комбинацию последовательных и параллельных соединений, как показано на рис. 8.13. Чтобы найти чистую емкость таких комбинаций, мы идентифицируем части, которые содержат только последовательные или только параллельные соединения, и находим их эквивалентные емкости. Мы повторяем этот процесс, пока не сможем определить эквивалентную емкость всей сети. Следующий пример иллюстрирует этот процесс.

Рисунок 8.13 а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов.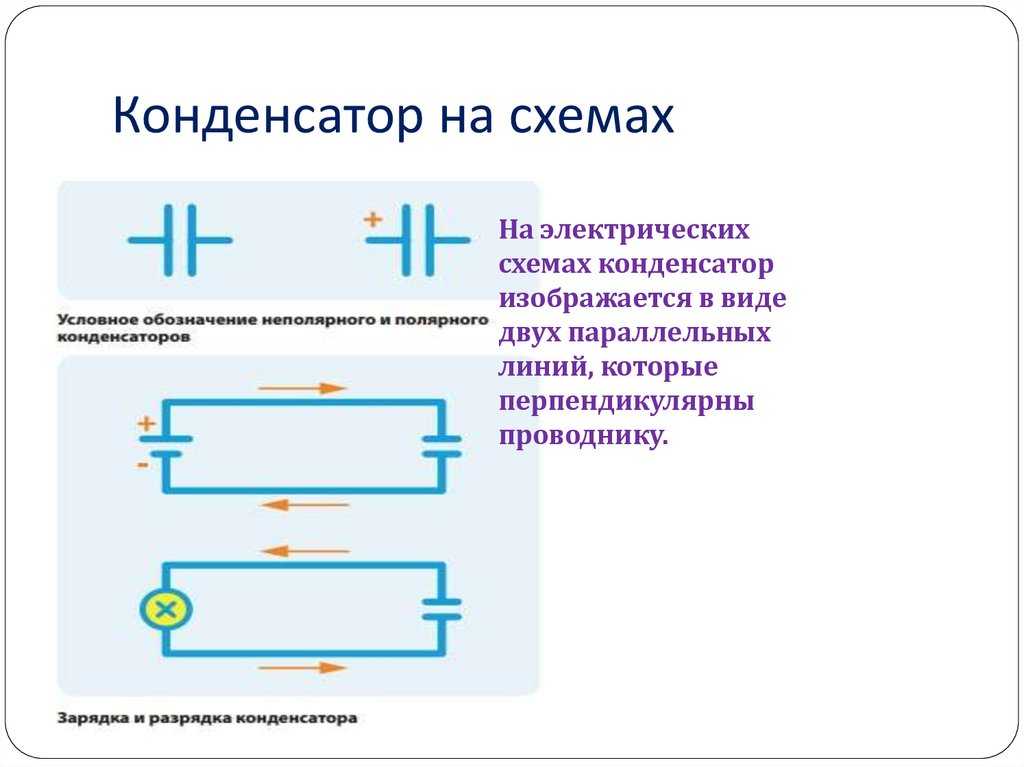 (б) C1C1 и C2C2 соединены последовательно; их эквивалентная емкость CS.CS. (c) Эквивалентная емкость CSCS подключена параллельно C3.C3. Таким образом, эквивалентная емкость всей сети представляет собой сумму CSCS и C3.C3.

Пример 8,6

Эквивалентная емкость сети

Найдите общую емкость комбинации конденсаторов, показанной на рис. 8.13. Предположим, что емкости известны с точностью до трех знаков после запятой (C1=1,000 мкФ, C2=5,000 мкФ, (C1=1,000 мкФ, C2=5,000 мкФ, C3=8,000 мкФ).C3=8,000 мкФ). Округлите ответ до трех знаков после запятой.

Стратегия

Сначала мы определяем, какие конденсаторы подключены последовательно, а какие параллельно. Конденсаторы C1C1 и C2C2 включены последовательно. Их комбинация, обозначенная CS,CS, параллельна C3.C3.

Решение

Поскольку C1 и C2, C1 и C2 включены последовательно, их эквивалентная емкость CSCS получается с помощью уравнения 8. 7:

1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.1CS=1C1+1C2=11,000 мкФ+15,000 мкФ=1,200 мкФ⇒CS=0,833 мкФ.

Емкость CSCS подключена параллельно с третьей емкостью C3C3, поэтому мы используем уравнение 8.8, чтобы найти эквивалентную емкость C всей сети:

C=CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ. =CS+C3=0,833 мкФ+8,000 мкФ=8,833 мкФ.

Пример 8,7

Сеть конденсаторов

Определите чистую емкость C комбинации конденсаторов, показанной на рисунке 8.14, при следующих значениях емкости: C1=12,0 мкФ, C2=2,0 мкФ, C1=12,0 мкФ, C2=2,0 мкФ и C3=4,0 мкФ3=4,0 мкФ. Когда на комбинации сохраняется разность потенциалов 12,0 В, найти заряд и напряжение на каждом конденсаторе.

Рисунок 8.14 а) Комбинация конденсаторов. (b) Эквивалентная комбинация из двух конденсаторов.

Стратегия

Сначала мы вычисляем чистую емкость C23C23 параллельного соединения C2C2 и C3C3. Тогда C — чистая емкость последовательного соединения C1C1 и C23C23. Мы используем соотношение C=Q/VC=Q/V, чтобы найти заряды Q1Q1, Q2Q2 и Q3Q3, а также напряжения V1V1, V2V2 и V3V3 на конденсаторах 1, 2 и 3 соответственно.

Раствор

Эквивалентная емкость для C2C2 и C3C3 равна

C23=C2+C3=2,0 мкФ+4,0 мкФ=6,0 мкФ.C23=C2+C3=2,0 мкФ+4,0 мкФ=6,0 мкФ.

Вся комбинация из трех конденсаторов эквивалентна двум конденсаторам, включенным последовательно,

1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.1C=112,0 мкФ+16,0 мкФ=14,0 мкФ⇒C=4,0 мкФ.

Рассмотрим эквивалентную комбинацию из двух конденсаторов на рис. 8.14(b). Поскольку конденсаторы соединены последовательно, они имеют одинаковый заряд Q1=Q23Q1=Q23. Кроме того, конденсаторы имеют общую разность потенциалов 12,0 В, так что Q112,0 мкФ+Q16,0 мкФ⇒Q1=48,0 мкКл.

Теперь разность потенциалов на конденсаторе 1 равна

V1=Q1C1=48,0 мкC12,0 мкФ=4,0 В.