Логика таблица истинности. Логические операции и таблицы истинности: основы математической логики

Что такое конъюнкция и дизъюнкция в логике. Как выглядят таблицы истинности для основных логических операций. Какой порядок выполнения логических операций в сложных выражениях. Как применяются логические операции на практике.

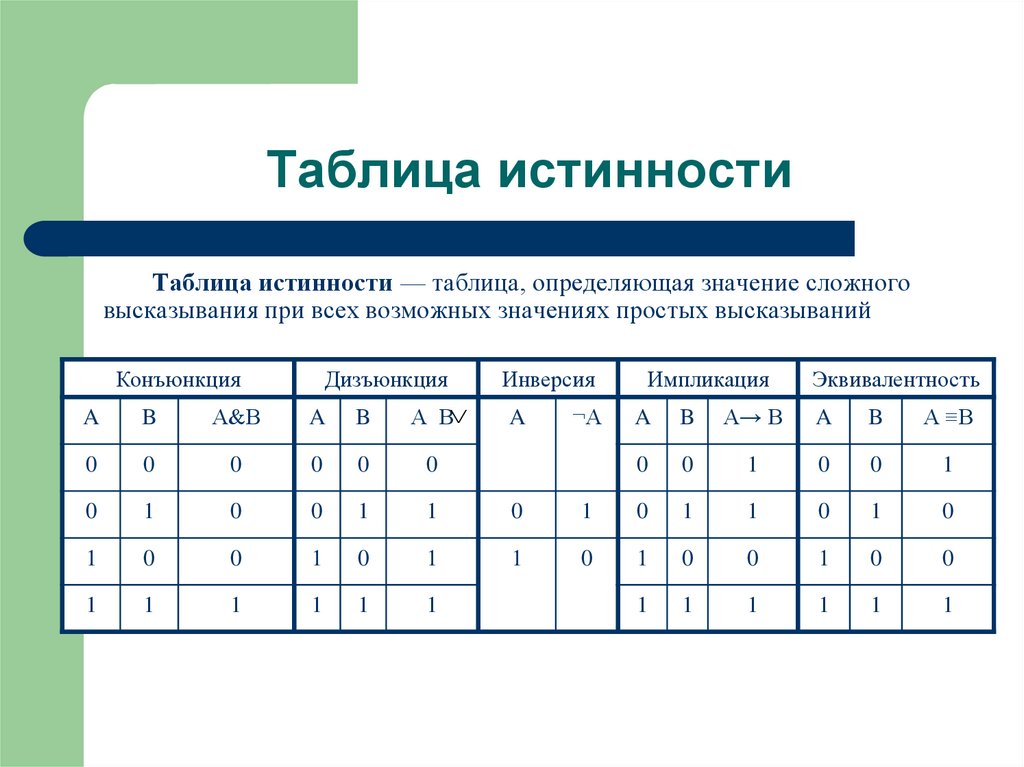
Основные логические операции и их таблицы истинности

Математическая логика оперирует высказываниями, которые могут быть либо истинными, либо ложными. Для работы с такими высказываниями используются логические операции. Рассмотрим основные из них:

Конъюнкция (логическое И)

Конъюнкция обозначается символом ∧ и соответствует союзу «и» в естественном языке. Результат конъюнкции истинен только если истинны оба высказывания.

Таблица истинности для конъюнкции:

A	B	A ∧ B
1	1	1
1	0	0
0	1	0
0	0	0

Дизъюнкция (логическое ИЛИ)

Дизъюнкция обозначается символом ∨ и соответствует союзу «или» в естественном языке. Результат дизъюнкции истинен, если истинно хотя бы одно из высказываний.

Таблица истинности для дизъюнкции:

A	B	A ∨ B
1	1	1
1	0	1
0	1	1
0	0	0

Отрицание и импликация в логике

Помимо конъюнкции и дизъюнкции, важную роль в математической логике играют отрицание и импликация.

Отрицание

Отрицание обозначается символом ¬ и меняет истинностное значение высказывания на противоположное.

Таблица истинности для отрицания:

A	¬A
1	0
0	1

Импликация

Импликация обозначается символом → и выражает логическое следование. Она ложна только в случае, когда из истинного высказывания следует ложное.

Таблица истинности для импликации:

A	B	A → B
1	1	1
1	0	0
0	1	1
0	0	1

Эквивалентность и исключающее ИЛИ

Для полноты картины рассмотрим еще две важные логические операции — эквивалентность и исключающее ИЛИ.

Эквивалентность

Эквивалентность обозначается символом ↔ и истинна тогда и только тогда, когда оба высказывания имеют одинаковое истинностное значение.

Таблица истинности для эквивалентности:

A	B	A ↔ B
1	1	1
1	0	0
0	1	0
0	0	1

Исключающее ИЛИ

Исключающее ИЛИ (XOR) обозначается символом ⊕ и истинно тогда и только тогда, когда истинно ровно одно из высказываний.

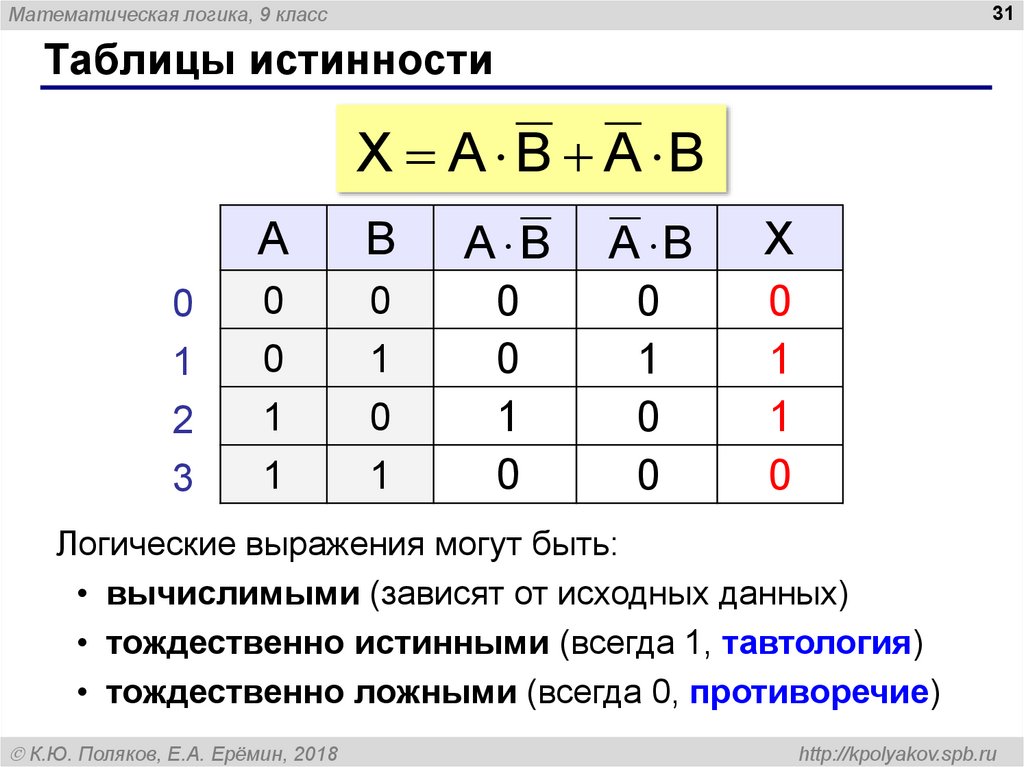
Таблица истинности для исключающего ИЛИ:

A	B	A ⊕ B
1	1	0
1	0	1
0	1	1
0	0	0

Порядок выполнения логических операций

При работе со сложными логическими выражениями важно помнить о порядке выполнения операций. Стандартный порядок следующий:

1. Отрицание (¬)
2. Конъюнкция (∧)
3. Дизъюнкция (∨)
4. Импликация (→)
5. Эквивалентность (↔)

Для изменения порядка выполнения операций используются скобки, как и в обычной арифметике.

Применение логических операций в информатике

Логические операции широко применяются в различных областях информатики и программирования. Рассмотрим несколько примеров:

Булева алгебра и цифровая электроника

Логические операции являются основой булевой алгебры, которая, в свою очередь, лежит в основе работы цифровых электронных схем. Логические вентили, такие как AND, OR, NOT, реализуют соответствующие логические операции на уровне электрических сигналов.

Условные операторы в программировании

В большинстве языков программирования условные операторы (if-else) используют логические выражения для определения потока выполнения программы. Например:

if (age >= 18 && hasLicense) {
    allowDriving();
} else {
    denyDriving();
}

Поисковые системы и базы данных

Логические операции используются для формирования сложных поисковых запросов. Например, запрос «кошки AND (рыжие OR полосатые) NOT бесшерстные» найдет информацию о рыжих или полосатых кошках, исключив бесшерстные породы.

Логические парадоксы и их роль в развитии математической логики

Изучение логических операций и их свойств привело к открытию интересных парадоксов, которые сыграли важную роль в развитии математической логики. Рассмотрим некоторые из них:

Парадокс лжеца

Классический парадокс лжеца формулируется так: «Это утверждение ложно». Если оно истинно, то оно ложно, а если ложно, то истинно. Этот парадокс привел к развитию теории типов и иерархии языков.

Парадокс Рассела

Парадокс Рассела связан с определением множества всех множеств, которые не содержат себя в качестве элемента. Этот парадокс привел к пересмотру оснований теории множеств и разработке аксиоматических систем.

Теоремы Гёделя о неполноте

Курт Гёдель доказал, что в любой достаточно сильной формальной системе существуют утверждения, которые невозможно ни доказать, ни опровергнуть в рамках этой системы. Это открытие имело огромное влияние на философию математики и логики.

Нечеткая логика и многозначная логика

Классическая двузначная логика не всегда адекватно описывает реальный мир. Поэтому были разработаны альтернативные логические системы:

Нечеткая логика

В нечеткой логике истинностное значение может быть любым числом от 0 до 1, что позволяет моделировать неопределенность и неточность. Нечеткая логика широко применяется в системах управления и искусственном интеллекте.

Многозначная логика

Многозначная логика оперирует более чем двумя истинностными значениями. Например, трехзначная логика Лукасевича вводит третье значение «неопределенно», что позволяет работать с неполной информацией.

Заключение

Логические операции и таблицы истинности являются фундаментальными понятиями математической логики. Они находят широкое применение в информатике, электронике, философии и других областях. Понимание логических операций и умение работать с ними необходимо для эффективного анализа и решения сложных проблем в различных сферах деятельности.

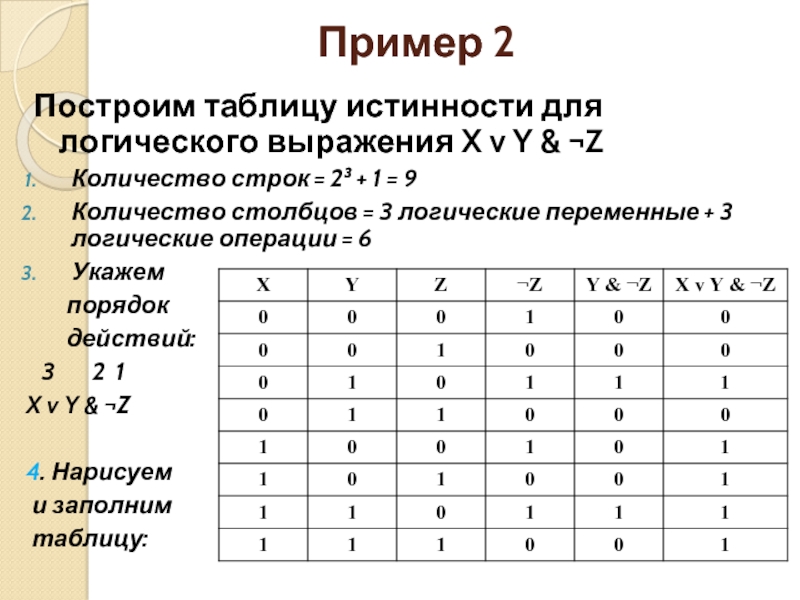
Основы логики. Логические операции и таблицы истинности

Содержание:

• Глоссарий, определения логики
• Логические операции и таблицы истинности
• Порядок выполнения логических операций в сложном логическом выражении

На данной странице будут рассмотренны 5 логических операций: конъюнкция, дизъюнкция, инверсия, импликация и эквивалентность, которых Вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам воспользоваться нашими программами для решения задач по математике, геометрии и теории вероятности. Помоми большого количества программ для решения задач на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!

Глоссарий, определения логики

Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).

Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.

Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).

Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.

Логические операции и таблицы истинности

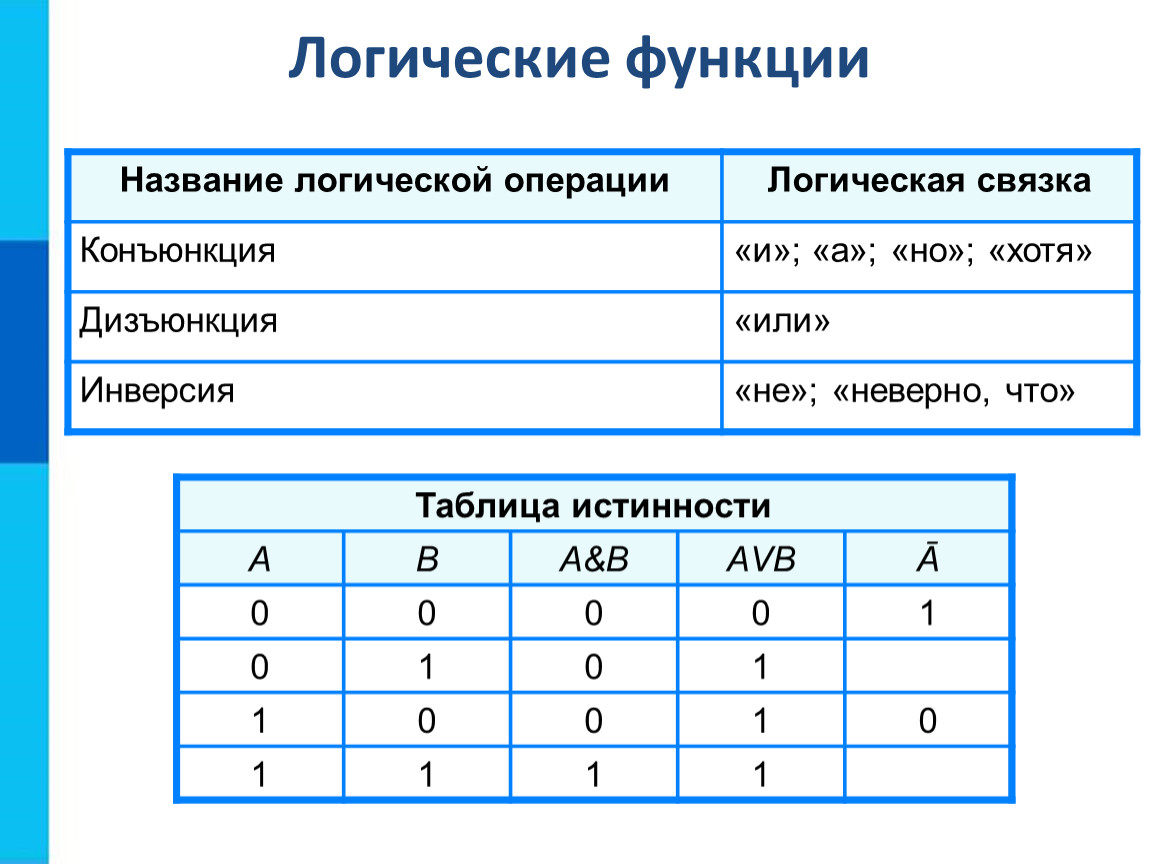
1) Логическое умножение или конъюнкция:

Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.

Обозначение: F = A & B.

Таблица истинности для конъюнкции

A	B	F
1	1	1
1	0	0
0	1	0
0	0	0

2) Логическое сложение или дизъюнкция:

Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.

Обозначение: F = A + B.

Таблица истинности для дизъюнкции

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

3) Логическое отрицание или инверсия:

Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Таблица истинности для инверсии

A	неА
1	0
0	1

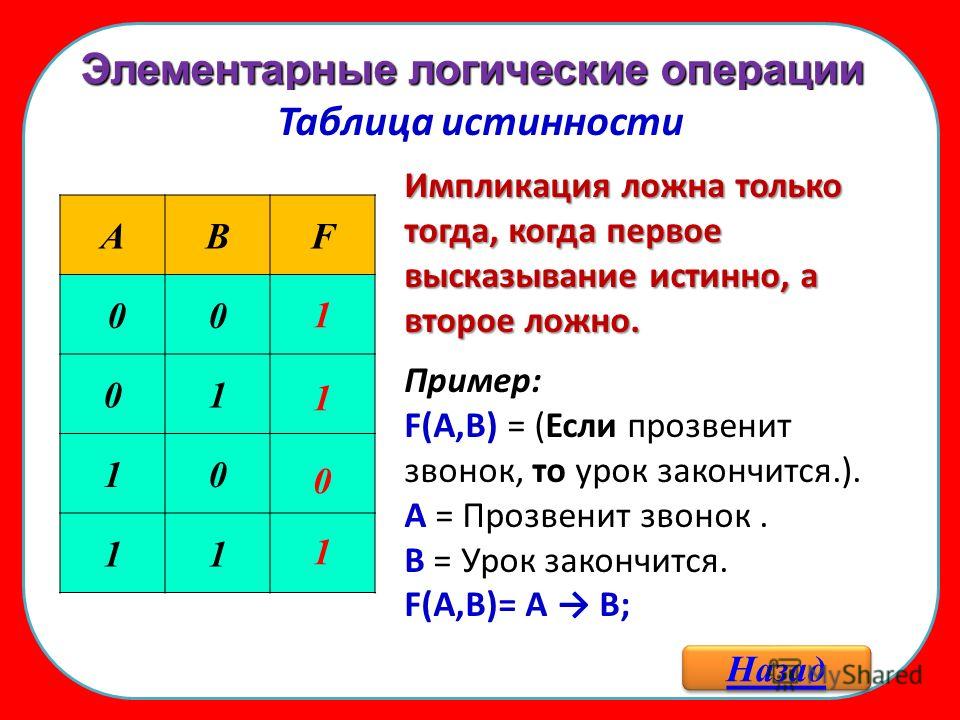
4) Логическое следование или импликация:

Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

Таблица истинности для импликации

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

5) Логическая равнозначность или эквивалентность:

Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.

Таблица истинности для эквивалентности

A	B	F
1	1	1
1	0	0
0	1	0
0	0	1

Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.

Для изменения указанного порядка выполнения логических операций используются скобки.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Основы логики, логические операции и таблицы истинности

Конъюнкция

«Конъюнкция» это одна из логических операций наряду с дизъюнкцией, инверсией, импликацией и эквивалентности. Иначе её называют логической «И». В программировании её обозначают чаще всего как «and» или «&» Считается истинным только в одном случае, когда оба операнда (оба сравниваемых элемента, если по простому) являются истинными (true, 1). В остальных же случаях, где какой либо из операндов ложный, или ложны оба, значения выражения будет ложно.

Для наглядности смотрите таблицу:

Таблица истинности

конъюнкция

«A«	«B«	«A» и «B»
1	1	1
1	0	0
0	1	0
0	0	0

Таблица истинности Конъюнкция

Конъюнкция может быть бинарной, то есть иметь всего два операнда (как например «A» «B») тернарной («A» «B» «C») или вообще иметь сколько угодно операндов, ( в этом случае она будет называться N-арной операцией) где n любое число.

Обозначения

Как я уже писал выше обозначения Конъюнкции встречаются совершенно разные приведу примеры:

a ⋀ b, a & b, a and b, a * b , ab в последнем варианте знак умножения точка может быть пропущен как и в обычном умножении. Как например в записи формулы используется запись подряд 7a + 2b где умножение между семеркой и «a» нету. Чаще всего используют запись «перевернутой галочки», ⋀ где она больше всего распространена в математике.

Дизъюнкция

Дизъюнкция — логическая операция которая обозначает логическое сложение. можно обозначить как «ИЛИ» потому что этот союз максимально похоже отражает суть дизъюнкции. Или этот операнд или тот, или сразу оба.

Также как и конъюкция это логическое выражение может быть двоичной или сколько угодно n- арной.

Считается истиной в почти во всех случаях кроме как два операнда ложных (False, 0)

Таблица истинности для дизъюнкции

A	B	«A» или «B»
1	1	1
1	0	1
0	1	1
0	0	0

Таблица истинности Дизъюнкция

Обозначения

Дизъюнкцию чаще всего записывают как

a ⋁ b, a || b, a | b, a OR b, обратите пожалуйста внимание что в первом случае это не буква V, а другой знак «галочка вниз» которая обозначает дизъюнкцию

Инверсия

С инверсией всё достаточно просто, оно преобразует операнд в обратный ему. Например если изначально у нас было ложное высказывание, то оно станет истинным, а истинное же с инверсией станет ложным.

Обозначение

Обозначается оно обычно ¬, или записывается как «НЕ»

Таблица истинности

Инверсия

A	не «А«
1	0
0	1

Таблица истинности инверсия

Абсолютно ничего сложного.

Давайте теперь рассмотрим следующую логическую операцию:

Импликация

Таблица импликация

A	B	«A» → «B»
1	1	1
1	0	0
0	1	1
0	0	1

Таблица истинности импликация

Обозначение

Обознается обычно знаком стрелочка →

Эквивалентность

Таблица

Эквивалентность

A	B	«A» ‘B»
1	1	1
1	0	0
0	1	0
0	0	1

Таблица истинности Эквивалентность

Обозначение

обычно обозначается символом ≡ или ↔

таблиц истинности | Brilliant Math & Science Wiki

Гаутам Шарма, Ноэль Ло, Джефф Пиллинг, и

способствовал

Содержимое

• Союз (И)
• Разъединение (ИЛИ)
• Отрицание
• Условные операторы или операторы импликации
• Семья из семи человек
• Биусловная логика
• Логические ворота
• Объединение аргументов (в процессе)
• Смотрите также

Два простых утверждения можно преобразовать с помощью слова «и» в составное утверждение, называемое союзом исходных утверждений. Мы используем символ \(\клин \) для обозначения соединения. Если \(p\) и \(q\) два простых утверждения, то \(p \клин q\) обозначает конъюнкцию \(p\) и \(q\) и читается как «\(p \) и \(q\).» \(_\квадрат\)

Таблица истинности для конъюнкции \(p \клин q\) двух простых утверждений \(p\) и \(q\):

• Утверждение \(p \клин q\) имеет значение истинности T всякий раз, когда и \(p\), и \(q\) имеют значение истинности T.
• Утверждение \(p \клин q\) имеет истинностное значение F, если либо \(p\), либо \(q\), либо оба имеют истинностное значение F.

Два простых утверждения можно преобразовать с помощью слова «или» в составное утверждение, называемое 9.0030 дизъюнкция исходных утверждений. Мы используем символ \(\vee \) для обозначения дизъюнкции. Если \(p\) и \(q\) два простых утверждения, то \(p\vee q\) обозначает дизъюнктность \(p\) и \(q\) и читается как «\(p \) или \(q\). » \(_\квадрат\)

Таблица истинности для дизъюнкции двух простых утверждений:

• Утверждение \(p\vee q\) имеет истинностное значение T всякий раз, когда либо \(p\) и \(q\), либо оба истинны значение т.
• Утверждение имеет истинностное значение F, если и \(p\), и \(q\) имеют истинностное значение F.

Утверждение, что утверждение ошибочно, или отрицание утверждения называется отрицанием утверждения. Отрицание утверждения обычно формируется путем введения слова «нет» в какое-либо надлежащее место в утверждении или путем добавления к утверждению префикса «это не так» или «это ложно». Отрицание утверждения \(p\) обозначается «\(\neg p.\)» \(_\квадрат\)

Таблица истинности для \(\neg p\):

Отрицание составных высказываний

а) Отрицание конъюнкции
\(\hspace{1cm}\)Отрицание конъюнкции \(p \клин q\) есть дизъюнкция отрицания \(p\ ) и отрицание \(q:\) \[\neg (p \wedge q) = {\neg p} \vee {\neg q}. \]

b) Отрицание дизъюнкции
\(\hspace {1cm}\) Отрицание дизъюнкции \(p \vee q\) есть конъюнкция отрицания \(p\) и отрицания \(q:\) \[\neg (p \vee q) ={\neg p} \клин {\neg q}.\]

c) Отрицание отрицания
\(\hspace{1cm}\) Отрицание отрицания утверждения есть само утверждение: \[\neg (\neg p) \equiv p.\]

У мистера и миссис Тан пятеро детей — Альфред, Бренда, Чарльз, Дариус, Эрик — предположительно разного возраста.

1. Если Чарльз не самый старший, то Альфред.

2. Если Эрик не самый младший, то Бренда.

3. Если Дариус не самый старший, то он сразу моложе Чарльза.

4. Если Альфред старше Бренды, то Дариус старше всех.

Определите порядок рождения пятерых детей с учетом вышеуказанных фактов.

---

Сдаем

• \(a\) быть предположением, что Чарльз не самый старший;
• \(b\) — утверждение, что Альфред — самый старший;
• \(c\) быть предположением, что Эрик не самый младший;
• \(d\) быть предположением, что Бренда самая младшая;
• \(e\) быть предположением, что Дариус не самый старший;
• \(f\) быть предположением, что Дарий чуть моложе Карла;
• \(g\) будет утверждением, что Альфред старше Бренды.

Из утверждения 1, \(a \стрелка вправо b\).
Из утверждения 2, \(c \rightarrow d\).
Из утверждения 3, \(e \rightarrow f\).
Из утверждения 4, \(g \rightarrow \neg e\), где \(\neg e\) обозначает отрицание \(e\).

Обратите внимание, что если Альфред самый старший \((b)\), то он старше всех своих четырех братьев и сестер, включая Бренду, поэтому \(b \rightarrow g\). Поскольку \(g \rightarrow \neg e\) (утверждение 4), \(b \rightarrow \neg e\) по транзитивности. Но если у нас есть \(b,\), что означает, что Альфред самый старший, логически следует, что \(e\), потому что Дарий не может быть самым старым (только один человек может быть самым старым). Переводя это, мы имеем \(b \rightarrow e\).

Следовательно, \((b \rightarrow e) \wedge (b \rightarrow \neg e) = (\neg b \vee e) \wedge (\neg b \vee \neg e) = \neg b \vee (e \клин \neg e) = \neg b \vee C = \neg b,\) где \(C\) означает противоречие. Единственный возможный вывод — \(\neg b\), где Альфред не самый старший. Из утверждения 1 \(a \стрелка вправо b\), то есть по modus tollens, \(\neg b \стрелка вправо \neg a\). Следовательно, Чарльз является самым старшим из .

Обратите внимание, что по чистой логике \(\neg a \rightarrow e\), где Чарльз, являющийся самым старшим, означает, что Дарий не может быть самым старым. Из утверждения 4, \(g \rightarrow \neg e\), поэтому по modus tollens \(e = \neg(\neg e) \rightarrow \neg g\). Из утверждения 3 \(e \rightarrow f\), таким образом, согласно modus ponens, наша дедукция \(e\) приводит к другой дедукции \(f\). С \(f\), так как Чарльз самый старший, Дариус должен быть вторым по старшинству .

Поскольку \(g\) означает, что Альфред старше Бренды, \(\neg g\) означает, что Альфред моложе Бренды , так как они не могут быть одного возраста. Поскольку есть кто-то моложе Бренды, она не может быть самой младшей, поэтому у нас есть \(\neg d\). Поскольку \(c \rightarrow d\) из утверждения 2, по modus tollens, \(\neg d \rightarrow \neg c\). Следовательно, Эрик — самый младший .

Учитывая все вычеты, выделенные жирным шрифтом, единственный возможный порядок рождения — Чарльз, Дариус, Бренда, Альфред, Эрик . \(_\квадрат\)

Биусловная логика — это способ соединить два утверждения, \(p\) и \(q\), логически говоря: «Утверждение \(p\) выполняется тогда и только тогда, когда выполняется утверждение \(q\)». В математике выражение «тогда и только тогда» часто сокращается до «iff», и приведенное выше утверждение может быть записано как

\[p \equiv q.\]

Таблица истинности для биусловной логики выглядит следующим образом:

\ [ \begin{выравнивание} {\color{Blue} \textbf{p}} &&{\color{Blue} \textbf{q}} &&{\color{Blue} p \equiv q} \\ \text{T} &&\text{T} &&\text{T} \\ \text{T} &&\text{F} &&\text{F} \\ \text{F} &&\text{T} &&\text{F} \\ \text{F} &&\text{F} &&\text{T} \end{выравнивание} \]

Это можно интерпретировать, рассмотрев следующее утверждение:

Я иду на пробежку тогда и только тогда, когда сегодня суббота. Это сочетает в себе оба следующих:

• Если это суббота, я иду на пробежку.
• Если я пойду на пробежку, то это будет суббота. (Или «Я бегаю только по субботам».)

Они согласуются только тогда, когда два утверждения «Сегодня я иду на пробежку» и «Сегодня суббота» верны или оба ложны, как показано в приведенной выше таблице.

Таблицы истинности часто используются в сочетании с логическими вентилями. Вот несколько распространенных примеров:

• Инвертор
• Буфер
• И
• ИЛИ
• НАНД
• НИ
• Исключающее ИЛИ
• Исключающее ИЛИ

Например, таблица истинности для вентиля И OUT = A & B задается следующим образом:

\[ \begin{align} {\color{Синий} \textbf{A}} &&{\color{Синий} \textbf{B}} &&{\color{Синий} \textbf{OUT}} \\ \текст{0} &&\текст{0} &&0 \\ \текст{0} &&\текст{1} &&0 \\ \текст{1} &&\текст{0} &&0 \\ \текст{1} &&\текст{1} &&1 \\ \end{выравнивание} \]

Таблица истинности для вентиля XOR OUT \(= A \oplus B\) представлена ​​следующим образом:

\[ \begin{align} {\color{Синий} \textbf{A}} &&{\color{Синий} \textbf{B}} &&{\color{Синий} \textbf{OUT}} \\ \текст{0} &&\текст{0} &&0 \\ \текст{0} &&\текст{1} &&1 \\ \текст{1} &&\текст{0} &&1 \\ \текст{1} &&\текст{1} &&0 \\ \end{align} \]

ВСЕГДА ПОМНИТЕ ЗОЛОТОЕ ПРАВИЛО: «И перед или»

При комбинировании аргументов таблицы истинности следуют одним и тем же шаблонам. Проще всего, но не всегда лучше решить их, разбив их на небольшие составные таблицы истинности.

\((p \rightarrow q ) \клин (q \vee p)\)

p \rightarrow q ||p||строка 1 столбец 2||q|| ||строка 2 столбец 1||строка 2 столбец 2||строка 2 столбец 1||строка 2 столбец 2||

• Логические элементы

• Логика высказываний

Процитировать как: Таблицы правды. Brilliant.org . Извлекаются из https://brilliant.org/wiki/truth-tables/

Страница не найдена | 979-230-3000

Можем ли мы помочь вам кое-что найти?

Вы можете использовать приведенные ниже ссылки, чтобы быстро перейти на некоторые из наших наиболее посещаемых страниц.
Если вы нашли неработающую ссылку, вы также можете сообщить об этом , чтобы мы могли ее исправить.

Зарегистрируйтесь и зарегистрируйтесь

Прием и регистрация

Приемная комиссия и регистратор могут помочь вам с различными вопросами, связанными с зачислением, такими как подача заявления, запрос выписок или регистрация для занятий .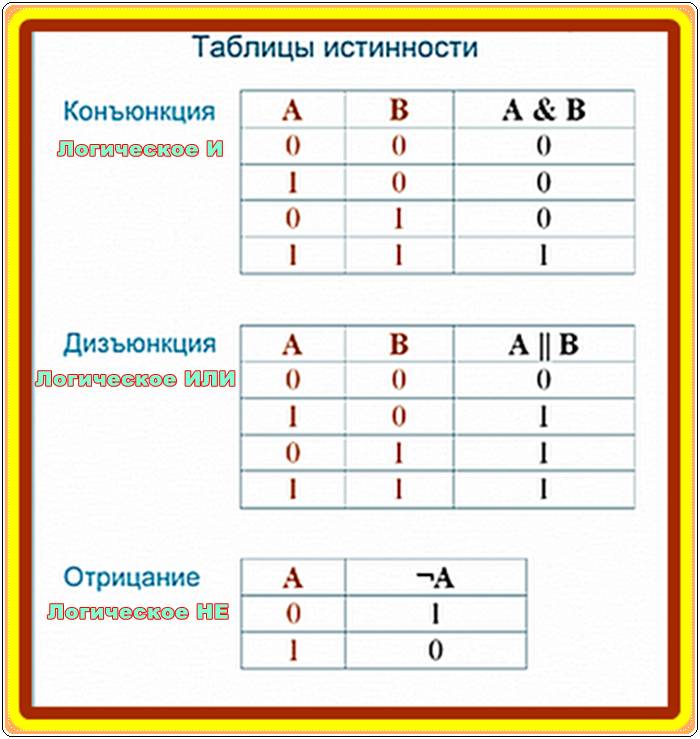

Свяжитесь с приемной комиссией и регистратором

Узнайте больше об очистке от менингита

Запросите или отправьте стенограммы

Консультирование

Наши консультанты и тренеры ACE It здесь, чтобы убедиться, что вы на правильном пути и выполнили все требования, чтобы вы были приняты, зачислены и на пути к успешному будущему.

Связь с консультированием и тестированием

Информация для студентов с двойным кредитом

Свяжитесь с тренером ACE It Coach

Плата за обучение в колледже

Финансовая помощь может помочь вам подать заявку на получение помощи, разобраться в типах помощи и получить предложенные средства. Вы можете совершать платежи и настраивать планы платежей в кассе.

Связь с отделом финансовой помощи

Связь с кассой (бизнес-офис)

Обязательное тестирование

Все новые студенты, стремящиеся к получению степени, должны сдать экзамен Texas Success Initiative (TSI). Чтобы поддержать наших студентов в этот кризис, мы теперь предоставляем услуги тестирования как онлайн, так и на территории кампуса.

Узнайте больше и зарегистрируйтесь на экзамен TSI

Пройдите предварительную аттестацию TSI перед сдачей экзамена TSI

Подготовка к занятиям

Помощь по технологиям 9024 1

У нас есть ноутбуки, точки доступа и гиды помочь настроить электронную почту на телефоне. Отдел дистанционного обучения может помочь ответить на вопросы, касающиеся виртуального кампуса (D2L).

Узнайте, как сбросить пароль

Подключение к службе поддержки Virtual Campus (D2L)

Совершите экскурсию по виртуальному кампусу

Запросите личную точку доступа или ноутбук

Настройте электронную почту BC на своем iPhone или Android

Получение оценки

Служба академической поддержки

Проблемы с ваши занятия? Мы здесь, чтобы помочь. Мы работали над тем, чтобы перевести многие из наших служб поддержки в онлайн, чтобы вы могли получить помощь, необходимую для достижения успеха.

Связь с центром письма

Связаться с Центром математики

Связаться с библиотекарем 

Связаться с руководителем SI для получения помощи в курсе естественных наук

Посмотреть видео о Центре успеха студентов

Доступ к услугам в кампусе

Необходимо составить проверить или купить книгу? Такие службы, как книжный магазин и службы обучения, по-прежнему открыты, чтобы помочь вам в течение семестра. Обратитесь в службу ИТ-поддержки, чтобы получить помощь с учетной записью учащегося и потребностями, связанными с технологиями.

Свяжитесь со службой ИТ-поддержки

Посетите веб-сайт книжного магазина Британской Колумбии

Составьте тест или получите помощь от Службы обучения

Рука помощи

Продовольственная и экстренная помощь 902 41

У нас есть экстренная помощь для помочь учащимся, которые испытывают большую неопределенность и стресс.

Свяжитесь с отделом здоровья и основных потребностей

Запросите информацию о GatorMart (Foodbank Британской Колумбии)

Посмотрите видео о GatorMart (Foodbank Британской Колумбии)

Подать заявку на экстренную помощь

Планирование образования и карьеры

Наша приверженность успеху учащихся лежит в основе всего, что мы делаем. Какими бы ни были ваши карьерные цели, мы здесь, чтобы помочь вам их достичь.

Связаться с тренером ACEit

Запрос на беседу с консультантом

Загляните в Центр карьеры

Посмотрите видео о Центре карьеры

Сделайте перерыв

Принять участие в виртуальном мероприятии

Мы здесь, чтобы продолжать помогать вам за пределами классной комнаты, предлагая качественные студенческие мероприятия и оздоровительные мероприятия, которые дополняют академические программы и улучшают образовательный опыт.

Просмотр предстоящих мероприятий

Свяжитесь с Управлением студенческой жизни

Свяжитесь с нами в социальных сетях 

Свяжитесь с группами в кампусе через Facebook и получайте новости обо всех событиях в Brazosport College через наши каналы в социальных сетях.