Мощность электрической цепи это. Электрическая мощность: определение, формулы и единицы измерения

Что такое электрическая мощность. Как рассчитать мощность в электрической цепи. Какие формулы используются для расчета мощности. В каких единицах измеряется электрическая мощность. Как связаны мощность, напряжение, ток и сопротивление.

Что такое электрическая мощность

Электрическая мощность — это скорость преобразования электрической энергии в другие виды энергии или работу. Другими словами, это количество электрической энергии, потребляемое или вырабатываемое электрической цепью за единицу времени.

Мощность характеризует интенсивность протекания энергетических процессов. Чем больше мощность, тем быстрее происходит преобразование энергии.

Формулы для расчета электрической мощности

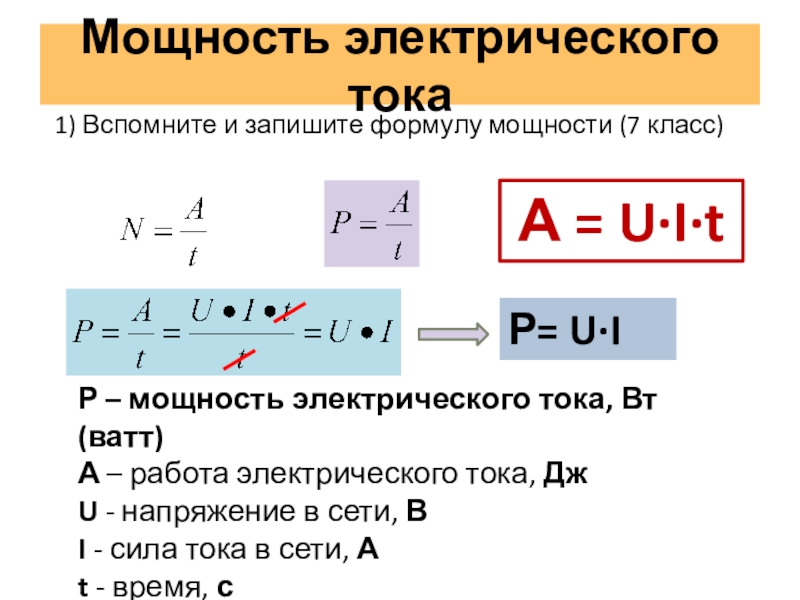
Основная формула для расчета мощности в электрической цепи:

P = I * U

где:

• P — мощность (Вт)
• I — сила тока (А)
• U — напряжение (В)

Также используются следующие формулы:

P = I^2 * R

P = U^2 / R

где R — сопротивление цепи (Ом).

Единицы измерения электрической мощности

Основная единица измерения мощности в Международной системе единиц (СИ) — ватт (Вт).

1 ватт равен мощности, при которой за 1 секунду совершается работа в 1 джоуль.

Производные единицы:

• киловатт (кВт) = 1000 Вт
• мегаватт (МВт) = 1 000 000 Вт
• гигаватт (ГВт) = 1 000 000 000 Вт

Как мощность связана с другими электрическими величинами

Электрическая мощность напрямую зависит от напряжения и силы тока в цепи. Чем выше напряжение или сила тока, тем больше мощность.

При постоянном напряжении мощность обратно пропорциональна сопротивлению: P = U^2 / R. То есть при увеличении сопротивления мощность уменьшается.

Примеры расчета электрической мощности

Рассмотрим несколько примеров расчета мощности в электрических цепях:

Пример 1

Дано: напряжение U = 220 В, сила тока I = 5 А.

Найти: мощность P.

Решение: P = U * I = 220 В * 5 А = 1100 Вт = 1,1 кВт

Пример 2

Дано: напряжение U = 12 В, сопротивление R = 6 Ом.

Найти: мощность P.

Решение: P = U^2 / R = 12^2 / 6 = 144 / 6 = 24 Вт

Применение понятия электрической мощности

Понятие электрической мощности широко используется в различных областях:

• Расчет потребления электроэнергии бытовыми приборами и промышленным оборудованием
• Проектирование электрических сетей и систем электроснабжения
• Выбор проводов, кабелей и защитной аппаратуры
• Оценка эффективности электрических устройств
• Расчет тепловых потерь в проводниках

Активная, реактивная и полная мощность

В цепях переменного тока различают три вида мощности:

• Активная мощность P — мощность преобразования электрической энергии в другие виды (тепло, механическую работу и т.д.)
• Реактивная мощность Q — мощность колебаний энергии между источником и приемником
• Полная мощность S — геометрическая сумма активной и реактивной мощностей

Для цепей переменного тока используется понятие коэффициента мощности — отношения активной мощности к полной.

Как измерить электрическую мощность

Для измерения электрической мощности используются специальные приборы — ваттметры. Принцип их работы основан на одновременном измерении тока и напряжения.

В бытовых условиях мощность можно определить по показаниям амперметра и вольтметра, используя формулу P = I * U.

Также мощность указывается в паспортных данных электроприборов и оборудования.

Потери мощности в электрических цепях

При передаче электроэнергии неизбежно возникают потери мощности, связанные с нагревом проводников. Мощность потерь пропорциональна квадрату силы тока и сопротивлению проводника:

P_потерь = I^2 * R

Для снижения потерь используют:

• Провода большего сечения (меньшее сопротивление)
• Высокое напряжение при передаче (меньший ток)
• Материалы с низким удельным сопротивлением

Мощность в цепях постоянного и переменного тока

В цепях постоянного тока мгновенная, средняя и действующая мощности совпадают.

В цепях переменного тока мгновенная мощность постоянно меняется. Для расчетов используют среднюю за период мощность, которая равна активной мощности.

При этом действующие значения напряжения и тока связаны с амплитудными значениями:

U_действ = U_амп / √2

I_действ = I_амп / √2

Влияние частоты на мощность в цепях переменного тока

В цепях переменного тока частота влияет на реактивную мощность, связанную с катушками индуктивности и конденсаторами:

• Для катушки индуктивности: Q_L = ω * L * I^2, где ω = 2πf — угловая частота
• Для конденсатора: Q_C = ω * C * U^2

При увеличении частоты растет реактивная мощность катушек и уменьшается реактивная мощность конденсаторов.

Оптимизация энергопотребления

Для снижения потребляемой мощности и повышения энергоэффективности применяют:

• Энергосберегающие технологии и оборудование
• Компенсацию реактивной мощности
• Оптимизацию режимов работы электроустановок
• Снижение потерь в линиях электропередачи
• Применение возобновляемых источников энергии

Это позволяет сократить расходы на электроэнергию и уменьшить нагрузку на электрические сети.

Емкость и мощность 📙 электрической цепи

1. Понятие мгновенной мощности
2. Понятие об идеальной емкости
3. Электрические цепи с конденсаторами

Электрическая энергия транспортируется электрическими цепями. Передачу энергии обозначают буквой w. Преобразование электроэнергии в другие виды энергии сопровождается различными процессами определенной интенсивности.

Интенсивность транспортировки и трансформации электрической энергии называют мощностью и обозначают буквой \(p\)

Мощность рассчитывается следующим образом:

\(p= {dw \over dt}\)

То есть, мощность показывает количество энергии dw, переданное за определенное время \(dt.\) По тому же принципу рассчитывается рассеивание энергии за определенное время.

Для расчета мгновенной мощности используют формулу следующего вида:

\(p=ui,\)

где \(u\) — мгновенное напряжение;

       \(i\) — мгновенная сила тока.

Мгновенная мощность состоит из постоянной и гармонической частей.

Значение угловой частоты мгновенной мощности вдвое выше угловой частоты тока и напряжения. Если мгновенная мощность со знаком «минус», это значит, что энергия перемещается обратно к источнику. Также это значит, что в двухполюснике направление напряжения противоположно току.

Такая картина наблюдается, когда есть запас магнитной и электрической энергии в катушке и конденсаторе, что входят в состав двухполюсника.

Активной мощностью является усредненное значение мгновенной мощности, взятой за отдельный период времени

\(P=UIcosφ\)

Если речь идет о пассивном двухполюснике, то активная мощность не может принимать минусовых значений. При входе в пассивный двухполюсник значение \(cosφ≥0.\) Теоретически возможна ситуация, когда \(P=0,\) но лишь для двухполюсника, который не содержит активных сопротивлений, но включает конденсатор емкости и катушку индуктивности.

Идеальную емкость в электрических цепях представляет конденсатор. Конденсатор и катушка индуктивности не потребляют мощность, в них \(P=0. \) То есть в данных элементах не осуществляется невозвратная трансформация энергии в иные ее виды, в них циркулирует имеющаяся энергия. Иными словами, электроэнергия запасается в магнитном поле катушки и электрическом поле конденсатора. Этот процесс занимает около четверти периода, после чего она направляется обратно в цепь.

Благодаря происходящим в катушке и конденсаторе процессам, они получили название реактивных элементов. Соответствующим образом и их сопротивления называются реактивными. А вот резистор имеет активное сопротивление.

При обмене энергией интенсивность характеризует максимальное значение скорости притока энергии в магнитное поле катушки и максимальное значение скорости притока энергии в электрическое поле конденсатора. Такая интенсивность является реактивной мощностью и рассчитывается так:

\(Q=UIsinφ\)

При нагрузке на индуктивности \(φ≥0\) реактивная мощность принимает только плюсовые значения. В случае опережающего тока нагрузки емкости – минусовые.

Реактивная мощность идеальной катушки соответствует наибольшему значению запаса энергии в катушке и частоты.

Коэффициентом мощности является соотношение полной и активной мощности. Его значение определяют как косинус угла смещения между током и напряжением

Наряду с полной и активной мощностью существует понятие комплексной мощности. Реактивная мощность является характеристикой циркуляции энергии между источником и приемником. Реактивный ток не производит никакой работы и это влечет за собой потери на силовых установках, а соответственно повышение мощности. Потому на сегодняшний день есть тенденция к увеличению мощности электрических сетей.

Некоторые приемники электроэнергии, например, двигатели, пользуются активно-индуктивной нагрузкой. Если к данной нагрузке подключить конденсатор, то общий ток приемника будет достигать величины фазы напряжения. То есть, он будет расти, но его общее значение будет падать при постоянной активной мощности. Все это влечет потери общего тока цепи.

Конденсаторы применяют для повышения мощности.

Конденсатор есть элементом электроцепи, который имеет емкость. Два проводника, которые расположены рядом, обладают определенной емкостью, но если их поверхность маленькая, то и емкость их будет незначительна, и обычно не берется во внимание.

Изучая электрические цепи, в них выделяют такие основные элементы, как источники питания, конденсаторы, катушки и сопротивления.

Конденсатор считается идеальным диэлектриком, потому его активное сопротивление приравнивается к нулю. Если к электрической цепи с конденсатором подвести напряжение, то в ней потечет электрический ток. При этом каждая из сторон конденсатора начнет накапливать заряд.

Величина емкости является одной из главных характеристик электрической цепи. Емкостью есть отношение абсолютного значения заряда одной из пластин к разнице потенциалов между пластинами. То есть, емкость предопределяет заряд в пластинах. Рассчитывается емкость так:

\(C= {q\over U}\)

Емкость характеризуют и в интегральной форме электрического поля на участке цепи. То есть на конденсаторе. Данная величина зависима от размеров конденсатора, формы электродов, характеристик среды между пластинами.

В международной системе СИ емкость измеряется в фарадах. Используют и другие единицы – нанофарады, микрофарады и прочие.

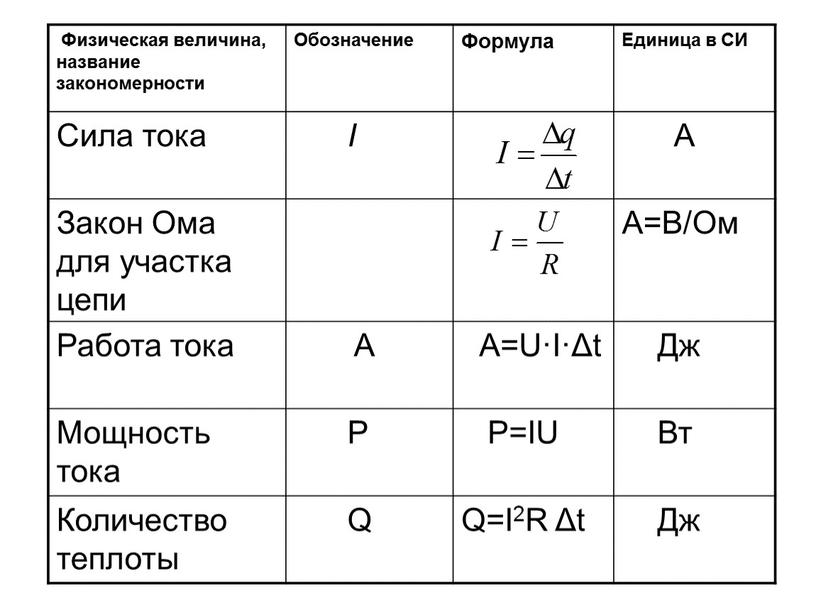
6.4. Мощность, выделяемая в электрической цепи. Коэффициент полезного действия источника тока

Электрические цепи обычно состоят из источника тока, подводящих проводов и сопротивления нагрузки. На рис.6.7 нарисована такая простейшая цепь. В этой цепи R является сопротивлением нагрузки,  – ЭДС источника тока, а через r мы обозначили внутреннее сопротивление источника тока; это сопротивление всегда присутствует в электрической цепи, содержащей источник тока.

Рис.6.7

Мощность, выделяемую в цепи, можно вычислить, используя определение мощности, введенное в курсе «Механика». По определению, мощностью называется работа, произведенная в единицу времени. Работу, возникающую на участке цепи, в которой течет ток i, можно записать dA = dqU = idtU. Следовательно, мощность, выделяемая в такой цепи, равна:

.

Таким образом, мощность, выделяемая в электрической цепи или на ее участке, равна произведению тока, текущего в этой цепи, на падение напряжения на этом участке цепи. Согласно полученному выражению, мощность, отдаваемая источником тока, определяется произведением ЭДС источника на силу тока, текущего в цепи:

P_= i.

По закону Ома для замкнутой цепи (см. рис.6.7) ток равен:

.

Таким образом, мощность, отдаваемая источником тока, равна:

.

Теперь найдем мощность, выделяемую в нагрузке R:

P_R = U_Ri.

По закону Ома падение напряжения на сопротивлении нагрузки U_R = iR. Следовательно:

.

Мы получили выражение, которое показывает, что мощность, выделяемая в нагрузке, меньше мощности, отдаваемой источником тока в электрическую цепь. Отсюда ясно, что часть мощности источника тратится не на нагрузку. В связи с этим вводится понятие коэффициента полезного действия источника тока, который обозначается через

 и определяется как отношение полезной мощности к полной или затраченной:

.

Из этого выражения видно, что коэффициент полезного действия всегда меньше единицы. На рис.6.8 приведены графики изменения полезной и затраченной мощности и коэффициента полезного действия при изменении сопротивления нагрузки.

Рис.6.8

На основании этих графиков можно сделать вывод, что максимальный коэффициент полезного действия равен единице, когда сопротивление нагрузки равно бесконечности, т. е. цепь разорвана. Но в этом случае и полезная, и затраченная мощности стремятся к нулю, т.е. этот режим не интересен. Когда сопротивление нагрузки равно нулю (короткое замыкание), источник тока выделяет в цепь максимальную мощность, но при этом полезная мощность и КПД равны нулю, значит, и этот режим не интересен. График изменения полезной мощности имеет экстремальный характер. Величину сопротивления, соответствующего максимальному значению полезной мощности, можно найти, приравняв первую производную от нее по сопротивлению к нулю. Тогда получаем

R_max = r. Для этого значения сопротивления нагрузки коэффи­циент полезного действия оказывается равным 0,5, а мощность, выделяемая в нагрузке, равна:

.

Как видно из полученного выражения, максимальная мощность, выделяемая в нагрузке, в четыре раза меньше максимальной мощности, выделяемой источником тока, и в два раза меньше той мощности, которую источник тока при данном сопротивлении выделяет в электрическую цепь.

19.4 Электроэнергетика — Физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Давать определение электрической мощности и описывать уравнение электрической мощности
• Расчет электрической мощности в цепях резисторов, соединенных последовательно, параллельно и комплексно

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

• (5) Научные понятия. Учащийся знает природу сил в физическом мире. Ожидается, что студент:
  • (Ж) проектировать, конструировать и рассчитывать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.

Кроме того, руководство по физике для средней школы рассматривает содержание этого раздела лабораторной работы под названием «Работа, энергия и мощность в цепях», а также следующие стандарты:

• (6) Научные концепции. Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
  • (С) рассчитать механическую энергию, мощность, генерируемую внутри, приложенный к ней импульс и импульс физической системы.

Основные термины раздела

электроэнергия

Энергия у многих ассоциируется с электричеством. Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи являются наглядными примерами электроснабжения. Мы также используем электроэнергию, чтобы заводить автомобили, компьютеры или освещать дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность – это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это значит, но и какие факторы определяют электрическую мощность.

Для начала давайте подумаем об лампочках, которые часто характеризуются номинальной мощностью в ваттах. Сравним лампочку мощностью 25 Вт с лампочкой мощностью 60 Вт (см. рис. 19.20). Хотя оба работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходная мощность электрической цепи определяется не напряжением, а чем-то иным.

Лампы накаливания, такие как две, показанные на рис. 19.20, по существу представляют собой резисторы, которые нагреваются, когда через них проходит ток, и нагреваются настолько, что излучают видимый и невидимый свет. Таким образом, две лампочки на фотографии можно рассматривать как два разных резистора. В простой цепи, такой как лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, как и напряжение, должен определять мощность.

Рисунок 19.20 Слева лампочка на 25 Вт, а справа лампочка на 60 Вт. Почему их выходная мощность различна, несмотря на то, что они работают на одном и том же напряжении?

Формулу мощности можно найти с помощью размерного анализа. Рассмотрим единицы мощности. В системе СИ мощность указывается в ваттах (Вт), что представляет собой энергию в единицу времени, или Дж/с

Вт=Джс.Вт=Джс.

19,47

Вспомним теперь, что напряжение — это потенциальная энергия на единицу заряда, а это означает, что единицы измерения напряжения составляют Дж/Кл

В=ДК.В=ДК.

19,48

Мы можем переписать это уравнение как J=V×CJ=V×C и подставить его в уравнение для ватт, чтобы получить

W=Js=V×Cs=V×Cs.W=Js=V× Cs=V×Cs.

Но кулон в секунду (Кл/с) — это электрический ток, который мы можем видеть из определения электрического тока, I=ΔQΔtI=ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или

П=IV.П=IV.

Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .

Например, рассмотрим схему на рис. 19.21. По закону Ома ток, протекающий через цепь, равен

I=VR=12V100Ω=0,12A.I=VR=12V100Ω=0,12A.

19,49

Таким образом, мощность, потребляемая схемой, равна

P=VI=(12 В)(0,12 А)=1,4 Вт. P=VI=(12 В)(0,12 А)=1,4 Вт.

19,50

Куда уходит эта сила? В этой схеме мощность идет в основном на нагрев резистора в этой цепи.

Рисунок 19.21 Простая схема, потребляющая электроэнергию.

При расчете мощности в цепи на рис. 19.21 мы использовали сопротивление и закон Ома для определения силы тока. Закон Ома дает ток: I=V/RI=V/R, который мы можем подставить в уравнение для электрической мощности, чтобы получить

P=IV=(VR)V=V2RP. P=IV=(VR)V= В2Р.

Мощность определяется только напряжением и сопротивлением.

Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электрической мощности и получить выражение для мощности только через ток и сопротивление. Если мы запишем закон Ома как V=IRV=IR и используя это, чтобы исключить V в уравнении P=IVP=IV, мы получаем

P=IV=I(IR)=I2R.P=IV=I(IR)=I2R.

Мощность определяется только током и сопротивлением.

Таким образом, комбинируя закон Ома с уравнением P=IVP=IV для электрической мощности, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (а не емкость или что-то еще), ток и напряжение. Это означает, что физической характеристикой цепи, которая определяет, сколько мощности она рассеивает, является ее сопротивление. Любые конденсаторы в цепи не рассеивают электроэнергию — напротив, конденсаторы либо накапливают электроэнергию, либо отдают ее обратно в цепь.

Чтобы понять, как связаны между собой напряжение, сопротивление, ток и мощность, рассмотрите рисунок 19.22, на котором показано колесо формул . Величины в центральной четверти окружности равны количествам в соответствующей внешней четверти окружности. Например, чтобы выразить потенциал V через мощность и ток, мы видим из круга формул, что V=P/IV=P/I.

Рисунок 19.22 Колесо формул показывает, как связаны вольты, сопротивление, ток и мощность. Количества во внутренних четвертях кругов равны количествам в соответствующих внешних четвертях кругов.

Рабочий пример

Найдите сопротивление лампочки

Типичная старая лампочка накаливания имела мощность 60 Вт. Если предположить, что на лампочку подается напряжение 120 В, какова сила тока через лампочку?

Стратегия

Нам известны напряжение и выходная мощность простой цепи, содержащей лампочку, поэтому мы можем использовать уравнение P=IVP=IV, чтобы найти ток I , протекающий через лампочку.

Решение

Решение P=IVP=IV для тока и вставка заданных значений напряжения и мощности дает

P=IVI=PV=60W120V=0,50A.P=IVI=PV=60W120V=0,50A.

19,51

Таким образом, через лампочку проходит полампера, когда на нее подается напряжение 120 В.

Обсуждение

Это значительный ток. Напомним, что бытовая электроэнергия является переменным, а не постоянным током, поэтому 120 В, подаваемые из бытовых розеток, представляют собой переменную, а не постоянную мощность. 120 В — это фактически усредненная по времени мощность, выдаваемая такими розетками. Таким образом, средний ток, проходящий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.

Рабочий пример

Грелки для ботинок

Чтобы согреть ботинки в холодные дни, вы решили вшить в стельку ботинок схему с резисторами. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите питать их от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление вы должны оказывать на каждую стельку?

Стратегия

Мы знаем желаемую мощность и напряжение (18 В, потому что у нас есть две 9-вольтовые батареи, соединенные последовательно), поэтому мы можем использовать уравнение P=V2/RP=V2/R, чтобы найти необходимое сопротивление.

Решение

Решая P=V2/RP=V2/R для сопротивления и подставляя данные напряжения и мощности, мы получаем

P=V2RR=V2P=(18V)210W=32Ω.P=V2RR=V2P=(18V )210 Вт=32 Ом.

19,52

Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.Ом.

Обсуждение

Давайте посмотрим, какой ток будет проходить по этой цепи. У нас есть 18 В, приложенные к сопротивлению 32 Ом, поэтому закон Ома дает

I=VR=18V32Ω=0,56A.I=VR=18V32Ω=0,56A.

19,53

Все аккумуляторы имеют маркировку, на которой указано, сколько заряда они могут обеспечить (в пересчете на ток, умноженный на время). Типичная щелочная батарея 9 В может обеспечить заряд 565 мА⋅чмА⋅ч. (таким образом, две 9-вольтовые батареи обеспечивают 1130 мА⋅чмА⋅ч ), поэтому эта система отопления будет работать в течение времени

t=1130×10−3A⋅ч0,56A=2,0ч.t=1130×10−3A⋅ч0. 56А=2,0ч.

19,54

Рабочий пример

Питание через ветвь цепи

Сопротивление каждого резистора в схеме ниже составляет 30 Ом. Какая мощность рассеивается на средней ветви цепи?

Стратегия

Средняя ветвь схемы содержит последовательно соединенные резисторы R3 и R5R3 и R5. Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем с помощью P=V2/RP=V2/R найдем мощность, рассеиваемую в ветви.

Решение

Эквивалентное сопротивление равно Rmiddle=R3+R5=30Ω+30Ω=60ΩRmiddle=R3+R5=30Ω+30Ω=60Ω . Мощность, рассеиваемая средней ветвью цепи, составляет

Pmiddle=V2Rmiddle=(12В)260Ом=2,4Вт. Pmiddle=V2Rmiddle=(12В)260Ом=2,4Вт.

19,55

Обсуждение

Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, выдаваемой батареей. Во-первых, эквивалентное сопротивление левой ветви составляет

Rleft=11/R1+1/R2+R4=11/30Ω+1/30Ω+30Ω=45Ω.Rleft=11/R1+1/R2+R4=11/ 30 Ом + 1/30 Ом + 30 Ом = 45 Ом.

19,56

Мощность через левую ветвь

Pleft=V2Rleft=(12В)245Ом=3,2Вт.Pleft=V2Rleft=(12В)245Ом=3,2Вт.

19,57

Правая ветвь содержит только R6R6, поэтому эквивалентное сопротивление Rright=R6=30ΩRright=R6=30Ω . Мощность через правую ветвь составляет

Pright=V2Rright=(12В)230Ом=4,8Вт.Pright=V2Rright=(12В)230Ом=4,8Вт.

19,58

Общая мощность, рассеиваемая цепью, представляет собой сумму мощностей, рассеиваемых в каждой ветви.

P=Pleft+Pmiddle+Pright=2,4W+3,2W+4,8W=10,4WP=Pleft+Pmiddle+Pright=2,4W+3,2W+4,8W=10,4W

19,59

Мощность, обеспечиваемая аккумулятором

П=IV. П=IV.

19,60

где I — общий ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить I . Ответвления вносят токи

0,40А.

19,61

Суммарный ток равен

I=Iлевый+Iсредний+Iправый=0,2667A+0,20A+0,40A=0,87A.I=Iлевый+Iсредний+Iправый=0,2667A+0,20A+0,40A=0,87A.

19,62

и мощность, обеспечиваемая аккумулятором, равна

P=IV=(0,87A)(12В)=10,4Вт.P=IV=(0,87А)(12В)=10,4Вт.

19,63

Это та же мощность, которая рассеивается на резисторах цепи, что показывает, что в этой цепи сохраняется энергия.

Практические задачи

16.

Какова формула мощности, рассеиваемой на резисторе?

1. Формула мощности, рассеиваемой на резисторе: P=IV. P=IV.
2. Формула для мощности, рассеиваемой на резисторе: P=VI.P=VI.
3. Формула для мощности, рассеиваемой на резисторе: P = IV .
4. Формула для мощности, рассеиваемой на резисторе: P = I ² В .

17.

Какова формула для мощности, рассеиваемой резистором, с учетом его сопротивления и напряжения на нем?

1. Формула для мощности, рассеиваемой на резисторе: P=RV2P=RV2
2. Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
3. Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
4. Формула для мощности, рассеиваемой на резисторе: P=I2RP=I2R

Проверьте свое понимание

18.

Какие элементы схемы рассеивают мощность?

1. конденсаторы
2. катушки индуктивности
3. идеальные переключатели
4. резисторы

19.

Объясните словами уравнение для мощности, рассеиваемой на данном сопротивлении.

1. Электрическая мощность пропорциональна току через резистор, умноженному на квадрат напряжения на резисторе.

2. Электрическая мощность пропорциональна квадрату тока через резистор, умноженному на напряжение на резисторе.

3. Электрическая мощность пропорциональна току через резистор, деленному на напряжение на резисторе.

4. Электрическая мощность пропорциональна току через резистор, умноженному на напряжение на резисторе.

Что такое сила? | Определение из TechTarget

К

• Участник TechTarget

См. также ток, напряжение, сопротивление и закон Ома.

Электрическая мощность — это скорость, с которой электрическая энергия преобразуется в другую форму, такую ​​как движение, тепло или электромагнитное поле. Обычным обозначением мощности является заглавная буква P. Стандартной единицей измерения является ватт, обозначаемый буквой W. В цепях общего пользования вместо него часто указывается киловатт (кВт); 1 кВт = 1000 Вт.

Один ватт — это мощность, полученная в результате рассеяния, преобразования или накопления энергии, эквивалентная одному джоулю в секунду. При выражении в ваттах мощность иногда называют ватт . Мощность в цепи постоянного тока (DC) равна произведению напряжения в вольтах и ​​силы тока в амперах. Это правило справедливо и для низкочастотных цепей переменного тока (AC), в которых энергия не накапливается и не высвобождается. При высоких частотах переменного тока, при которых энергия накапливается и высвобождается (а также рассеивается или преобразуется), выражение для мощности более сложное.

В цепи постоянного тока источник E вольт, отдающий I ампер, производит P Вт по формуле:

П = ЭИ

Когда ток 1 ампер проходит через сопротивление R Ом, то мощность в ваттах, рассеиваемая или преобразуемая этим компонентом, определяется по формуле:

Р = I ² Р

При разности потенциалов E В появляется на компоненте, имеющем сопротивление R Ом, тогда мощность в ваттах, рассеиваемая или преобразуемая этим компонентом, определяется по формуле:

Р = Е ² / Р

В цепи постоянного тока мощность является скалярной (одномерной) величиной. В общем случае переменного тока определение мощности требует двух измерений, поскольку мощность переменного тока является векторной величиной. Предполагая, что в цепи переменного тока нет реактивного сопротивления (противостояние переменному току, но не постоянному току), мощность можно рассчитать по приведенным выше формулам для постоянного тока, используя среднеквадратические значения переменного тока и напряжения. Если реактивное сопротивление существует, некоторая мощность попеременно накапливается и высвобождается системой. Это называется полной мощностью или реактивной мощностью. Сопротивление рассеивает энергию в виде тепла или преобразует ее в какую-либо другую осязаемую форму; это называется истинной силой. Векторная комбинация реактивного сопротивления и сопротивления известна как импеданс.

Последнее обновление: январь 2008 г.

враждебный ML

Состязательное машинное обучение — это метод, используемый в машинном обучении для обмана или введения в заблуждение модели с помощью злонамеренных входных данных.

Сеть

• межсоединение центра обработки данных (DCI)

  Технология соединения центров обработки данных (DCI) объединяет два или более центров обработки данных для совместного использования ресурсов.

• Протокол маршрутной информации (RIP)

  Протокол маршрутной информации (RIP) — это дистанционно-векторный протокол, в котором в качестве основного показателя используется количество переходов.

• доступность сети

  Доступность сети — это время безотказной работы сетевой системы в течение определенного интервала времени.

Безопасность

• кража учетных данных

  Кража учетных данных — это тип киберпреступления, связанный с кражей удостоверения личности жертвы.

• суверенная идентичность

  Самостоятельная суверенная идентификация (SSI) — это модель управления цифровой идентификацией, в которой отдельные лица или предприятия владеют единолично . ..

• Сертифицированный специалист по безопасности информационных систем (CISSP) Сертифицированный специалист по безопасности информационных систем

  (CISSP) — это сертификат информационной безопасности, разработанный …

ИТ-директор

• рассказывание историй о данных

  Рассказывание историй о данных — это процесс перевода анализа данных в понятные термины с целью повлиять на деловое решение…

• оншорный аутсорсинг (внутренний аутсорсинг)

  Оншорный аутсорсинг, также известный как внутренний аутсорсинг, представляет собой получение услуг от кого-то вне компании, но в пределах …

• FMEA (анализ видов и последствий отказов)

  FMEA (анализ видов и последствий отказов) представляет собой пошаговый подход к сбору сведений о возможных точках отказа в …

HRSoftware

• самообслуживание сотрудников (ESS)

  Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой . ..

• платформа обучения (LXP)

  Платформа обучения (LXP) — это управляемая искусственным интеллектом платформа взаимного обучения, предоставляемая с использованием программного обеспечения как услуги (…

• Поиск талантов

  Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …

Обслуживание клиентов

• виртуальный помощник (помощник ИИ)

  Виртуальный помощник, также называемый помощником ИИ или цифровым помощником, представляет собой прикладную программу, которая понимает естественный язык …

• жизненный цикл клиента

  В управлении взаимоотношениями с клиентами (CRM) жизненный цикл клиента — это термин, используемый для описания последовательности шагов, которые проходит клиент.