Какие основные параметры определяют характеристики линий связи. Как затухание, помехоустойчивость и полоса пропускания влияют на пропускную способность и достоверность передачи данных. Какие первичные и вторичные параметры используются для описания свойств линий связи.
Основные характеристики линий связи
Линии связи играют ключевую роль в работе любых телекоммуникационных систем и компьютерных сетей. От характеристик используемых линий связи напрямую зависят такие важные параметры, как скорость и надежность передачи данных. Рассмотрим основные характеристики, которые определяют качество линий связи:
- Затухание сигнала
- Помехоустойчивость
- Полоса пропускания
- Пропускная способность
- Достоверность передачи данных
Затухание сигнала в линиях связи
Затухание характеризует уменьшение мощности сигнала при его распространении по линии связи. Оно измеряется в децибелах и рассчитывается по формуле:
A = 10 log(Pвых / Pвх)
где Pвых — мощность сигнала на выходе линии, Pвх — мощность на входе.
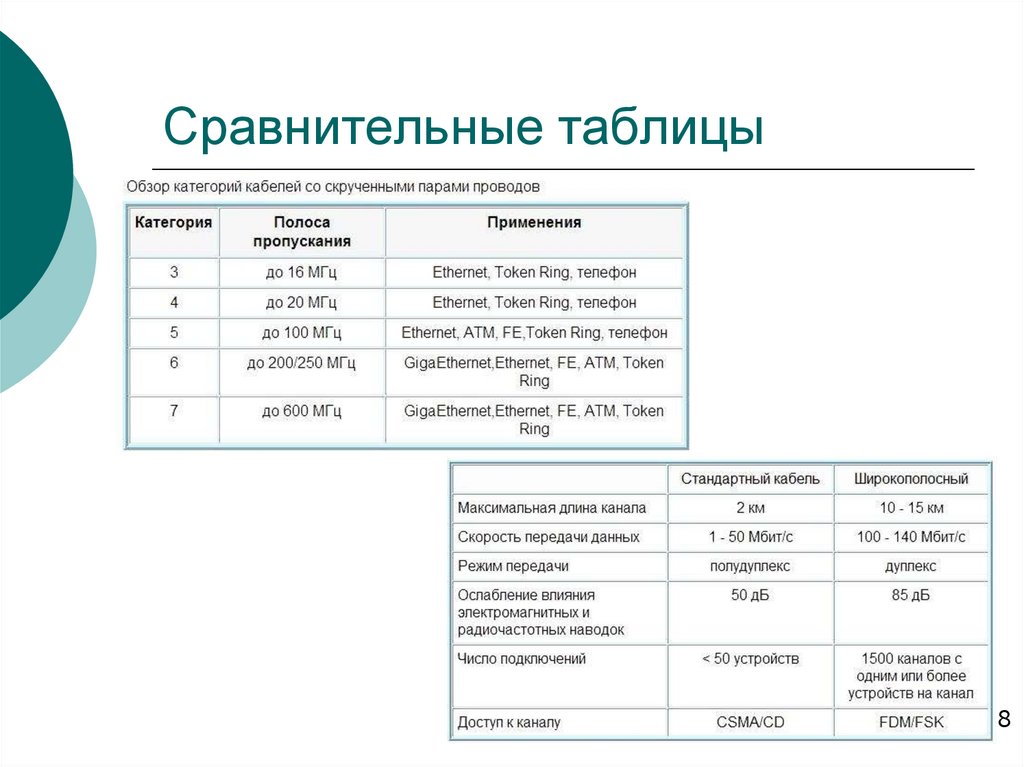
Чем меньше затухание, тем лучше качество линии связи. Например, для кабеля категории 5 затухание на частоте 100 МГц не должно превышать -23,6 дБ при длине 100 м.
Помехоустойчивость линий связи
Помехоустойчивость определяет способность линии подавлять внешние и взаимные помехи. Она зависит от типа среды передачи и применяемых методов экранирования.
Для оценки помехоустойчивости кабельных линий используются следующие параметры:
- Переходное затухание на ближнем конце (NEXT)
- Переходное затухание на дальнем конце (FEXT)
- Защищенность (ACR) — разность между уровнем полезного сигнала и помех
Чем выше значения этих параметров, тем лучше помехозащищенность линии связи.
Полоса пропускания линий связи
Полоса пропускания — это диапазон частот, в пределах которого затухание сигнала не превышает заданного уровня (обычно -3 дБ). Она определяет, какой спектр частот может быть передан по линии без значительных искажений.
Ширина полосы пропускания напрямую влияет на максимально возможную скорость передачи данных. Чем шире полоса, тем выше потенциальная пропускная способность линии связи.

Пропускная способность линий связи
Пропускная способность характеризует максимально возможную скорость передачи данных по линии связи. Она измеряется в битах в секунду (бит/с) и зависит от:
- Полосы пропускания линии
- Спектра передаваемых сигналов
- Способа физического и логического кодирования
Пропускная способность определяется не только характеристиками физической среды, но и используемыми протоколами физического уровня. Например, витая пара категории 3 может обеспечивать скорость 10 Мбит/с при кодировании 10Base-T и 33 Мбит/с при 100Base-T4.
Достоверность передачи данных
Достоверность характеризует вероятность искажения передаваемых битов информации. Она оценивается параметром BER (Bit Error Rate) — интенсивностью битовых ошибок.
Типичные значения BER для различных линий связи:
- 10^-4 — 10^-6 для кабельных линий без дополнительной защиты от ошибок
- 10^-9 для волоконно-оптических линий
Значение BER 10^-6 означает, что в среднем искажается 1 бит из миллиона переданных.
Первичные параметры линий связи
Первичные параметры характеризуют физическую природу линии связи. Для медных кабелей к ним относятся:
- Погонное активное сопротивление R0 (Ом/км)
- Погонная индуктивность L0 (Гн/км)
- Погонная емкость C0 (Ф/км)
- Погонная проводимость изоляции G0 (См/км)
Для оптических волокон важным первичным параметром является зависимость коэффициента преломления от расстояния до оптической оси.
Вторичные параметры линий связи
Вторичные параметры являются обобщенными характеристиками, не зависящими от физической природы линии. К ним относятся:
- Волновое сопротивление Zc (Ом)
- Коэффициент распространения γ
Вторичные параметры определяются через первичные и частоту сигнала:
Zc = √((R0 + jωL0) / (G0 + jωC0))
γ = √((R0 + jωL0)(G0 + jωC0))
где ω — круговая частота сигнала.
Влияние параметров на качество передачи данных
Рассмотренные характеристики линий связи оказывают комплексное влияние на качество передачи данных:
- Затухание и помехи ограничивают дальность передачи
- Полоса пропускания определяет максимальную скорость
- Достоверность влияет на надежность передачи
Улучшение этих параметров позволяет повысить пропускную способность и надежность линий связи. Поэтому при проектировании сетей важно учитывать все характеристики используемых линий связи.
Способы кодирования информации в линиях связи
Способ физического (линейного) кодирования определяет, как информация представляется в виде сигналов в линии связи. От выбранного способа зависят спектр сигналов и достижимая пропускная способность. Основные методы кодирования:
- Амплитудная модуляция
- Частотная модуляция
- Фазовая модуляция
- Импульсно-кодовая модуляция
Более сложные методы позволяют передавать несколько бит за один такт сигнала, увеличивая пропускную способность. Например, при квадратурной амплитудной модуляции QAM-64 передается 6 бит за такт.
Заключение
Характеристики линий связи играют ключевую роль в обеспечении высокой скорости и надежности передачи данных в телекоммуникационных системах. Понимание первичных и вторичных параметров, а также их влияния на пропускную способность и достоверность позволяет оптимально проектировать сети связи. При выборе линий необходимо учитывать весь комплекс их характеристик для достижения требуемого качества передачи информации.
Характеристики линий связи | Журнал сетевых решений/LAN
Производительность и надежность сети напрямую зависит от характеристик линий связи.
Характеристики линий связи можно разделить на две группы:
- параметры распространения характеризуют процесс распространения полезного сигнала в зависимости от собственных параметров линии, например погонной индуктивности медного кабеля;
- параметры влияния описывают степень влияния на полезный сигнал других сигналов — внешних помех, наводок от других пар проводников в медном кабеле.
В свою очередь, в каждой из этих групп можно выделить первичные и вторичные параметры. Первичные — характеризуют физическую природу линии связи: например, погонное активное сопротивление, погонную индуктивность, погонную емкость и погонную проводимость изоляции медного кабеля или зависимость коэффициента преломления оптического волокна от расстояния от оптической оси. Вторичные параметры выражают некоторый обобщенный результат процесса распространения сигнала по линии связи и не зависят от ее природы — например, степень ослабления мощности сигнала при прохождении им определенного расстояния вдоль линии связи, так называемое затухание сигнала. Для медных кабелей не менее важен и такой вторичный параметр влияния, как степень ослабления помехи от соседней витой пары.
Вторичные параметры определяются по отклику линии передачи на некоторые эталонные воздействия. Подобный подход позволяет достаточно просто и однотипно определять характеристики линий связи любой природы, не прибегая к сложным теоретическим исследованиям и построению аналитических моделей. Для исследования реакции линий связи чаще всего в качестве эталонных используются синусоидальные сигналы различных частот.
СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ НА ЛИНИЯХ СВЯЗИ
Любой периодический процесс можно представить в виде суммы синусоидальных колебаний различных частот и различных амплитуд (см. Рисунок 1). Каждую составляющую синусоиду называют также гармоникой, а набор всех гармоник — спектральным разложением исходного сигнала. Непериодические сигналы можно представить в виде интеграла синусоидальных сигналов с непрерывным спектром частот.
| Рисунок 1. Представление периодического сигнала в виде суммы синусоид. |
При передаче по линии связи форма сигнала искажается вследствие неодинаковой деформации синусоид различных частот. Если это аналоговый сигнал, передающий речь, то изменяется тембр голоса вследствие неточного воспроизведения обертонов — боковых частот. При передаче импульсных сигналов, характерных для компьютерных сетей, искажаются низкочастотные и высокочастотные гармоники, в результате фронты импульсов теряют свою прямоугольную форму (см. Рисунок 2). Поэтому на приемном конце линии сигналы могут плохо распознаваться.
| Рисунок 2. Искажение импульсов в линии связи. |
При передаче по линии связи сигналы искажаются из-за того, что ее физические параметры отличаются от идеальных. Так, например, медные провода всегда представляют собой некоторую распределенную по длине комбинацию активного сопротивления, емкостной и индуктивной нагрузки. В результате для синусоид различных частот линия будет обладать различным полным сопротивлением, а значит, и передаваться они будут по-разному. Волоконно-оптический кабель также имеет отклонения от идеальной среды для передачи света — вакуума. Если линия связи включает промежуточную аппаратуру, то и она может вносить дополнительные искажения.
Не только неоднородность внутренних физических параметров линии связи становится причиной неточных сигналов, свой вклад в искажение формы сигналов на выходе линии вносят и внешние помехи. Их создают различные электрические двигатели, электронные устройства, атмосферные явления и т. д. Несмотря на защитные меры, предпринимаемые разработчиками кабелей и усилительно-коммутирующей аппаратуры, полностью компенсировать влияние внешних помех не удается. Кроме того, в кабеле существуют и внутренние помехи — так называемые наводки одной пары проводников на другую. В результате сигналы на выходе линии связи обычно имеют сложную форму (как это и показано на Рисунке 2), по которой иногда трудно понять, какая дискретная информация была подана на вход линии.
Качество исходных сигналов (крутизна фронтов, общая форма импульсов) зависит от качества передатчика, генерирующего сигналы в линию связи. Одна из самых важных характеристик передатчика — спектральная, т.е. спектральное разложение генерируемых им сигналов. Для генерации качественных прямоугольных импульсов необходимо, чтобы спектральная характеристика передатчика представляла собой как можно более узкую полосу. Например, лазерные диоды имеют значительно меньшую ширину спектра излучения (1-2 нм) по сравнению со светодиодами (30—50 нм) при генерации импульсов, поэтому частота модуляции лазерных диодов может быть намного выше, чем светодиодов.
ЗАТУХАНИЕ И ВОЛНОВОЕ СОПРОТИВЛЕНИЕ
Степень искажения синусоидальных сигналов линиями связи оценивается с помощью таких характеристик, как затухание и полоса пропускания.
Затухание показывает, насколько уменьшается мощность эталонного синусоидального сигнала на выходе линии связи по отношению к мощности сигнала на входе этой линии. Затухание А обычно измеряется в децибелах (дБ) и вычисляется по следующей формуле:
А = 10 lg Рвых/Рвх,
где Pвых — мощность сигнала на выходе линии, а Рвх — мощность сигнала на ее входе.
При отсутствии промежуточных усилителей мощность выходного сигнала кабеля всегда меньше мощности входного, поэтому затухание кабеля, как правило, имеет отрицательную величину.
Степень затухания мощности синусоидального сигнала при прохождении им по линии связи обычно зависит от частоты синусоиды, поэтому полную характеристику дает лишь зависимость затухания от частоты во всем диапазоне, используемом на практике (Рисунок 3).
| Рисунок 3. Зависимость затухания от частоты. |
Чаще всего при описании параметров линии связи приводятся значения затухания всего в нескольких точках общей зависимости, при этом каждая из них соответствует определенной частоте, на которой измеряется затухание. Отдельное значение затухания называют коэффициентом затухания. Применение всего нескольких значений вместо полной характеристики связано, с одной стороны, со стремлением упростить измерения при проверке качества линии, а с другой, основная частота передаваемого сигнала часто заранее известна — это та частота, гармоника которой имеет наибольшую амплитуду и мощность. Поэтому достаточно знать уровень затухания на данной частоте, чтобы приблизительно оценить искажения передаваемых по линии сигналов. Более точные оценки возможны при знании затухания на различных частотах, соответствующих нескольким основным гармоникам передаваемого сигнала.
Чем меньше затухание, тем выше качество линии связи или кабеля, по которому она проложена. Обычно затухание определяют для пассивных участков линии связи, состоящих из кабелей и кроссовых секций, без усилителей и регенераторов. Например, кабель с витыми парами Категории 5 для внутренней проводки в зданиях, применяемой практически для всех технологий локальных сетей, характеризуется затуханием не ниже -23,6 дБ для частоты 100 МГц при длине кабеля 100 м.
Частота 100 МГц выбрана потому, что кабель этой категории предназначен для высокоскоростной передачи данных, чьи сигналы имеют значимые гармоники с частотой примерно 100 МГц. Более качественный кабель Категории 6 уже имеет на частоте 100 МГц затухание не ниже -20,6 дБ, т. е. мощность сигнала снижается в меньшей степени. Часто в документации приводятся абсолютные значения затухания, т. е. его знак опускается, так как затухание всегда отрицательно для пассивного, не содержащего усилители и регенераторы, участка линии, например непрерывного кабеля.
| Рисунок 4. Окна прозрачности оптического волокна. |
Оптический кабель отличается существенно более низкими (по абсолютной величине) размерами затухания, обычно в диапазоне от 0,2 до 3 дБ при длине кабеля в 1000 м. Практически всем оптическим волокнам свойственна сложная зависимость затухания от длины волны, с тремя так называемыми «окнами прозрачности». Характерный пример показан на Рисунке 4. Как можно видеть, область эффективного использования современных волокон ограничена волнами длин 850, 1300 и 1550 нм, при этом окно в 1550 нм обеспечивает наименьшие потери, а значит, максимальную дальность при фиксированной мощности передатчика и фиксированной чувствительности приемника. Выпускаемый многомодовый кабель обладает двумя первыми окнами прозрачности, т. е. 850 и 1300 нм, а одномодовый кабель — двумя окнами прозрачности в диапазонах 1310 и 1550 нм.
Мощность передатчика часто характеризуется абсолютным уровнем мощности сигнала. Уровень мощности, как и затухание, измеряется в децибелах. При этом в качестве базового принимается значение в 1 мВт. Таким образом, уровень мощности p вычисляется по следующей формуле:
p = 10 lg P/1 мВт [дБм],
где P — мощность сигнала в милливаттах, а дБм — единица измерения уровня мощности (дБ на 1 мВт).
Важным вторичным параметром распространения медной линии связи является ее волновое сопротивление. Этот параметр представляет собой полное (комплексное) сопротивление, которое электромагнитная волна определенной частоты встречает при распространении вдоль однородной цепи. Волновое сопротивление измеряется в Омах и зависит от таких первичных параметров линии связи, как активное сопротивление, погонная индуктивность и погонная емкость, а также от частоты самого сигнала. Выходное сопротивление передатчика должно быть согласовано с волновым сопротивлением линии, иначе затухание сигнала будет чрезмерно большим.
ПОМЕХОУСТОЙЧИВОСТЬ
Помехоустойчивость линии определяет ее способность уменьшать уровень помех со стороны внешней среды или проводников самого кабеля. Она зависит от типа используемой физической среды, от экранирующих и подавляющих помехи средств самой линии. Наименее помехоустойчивыми являются радиолинии, хорошей устойчивостью обладают кабельные линии и отличной — волоконно-оптические, малочувствительные к внешнему электромагнитному излучению. Обычно уменьшения помех от внешних электромагнитных полей добиваются экранированием и/или скручиванием проводников. Величины, характеризующие помехоустойчивость, относятся к параметрам влияния линии связи.
Первичные параметры влияния медного кабеля — электрическая и магнитная связи. Электрическая связь определяется отношением наведенного тока в цепи, подверженной влиянию, к напряжению, действующему во влияющей цепи. Магнитная связь — это отношение электродвижущей силы, наведенной в цепи, подверженной влиянию, к току во влияющей цепи. Результатом электрической и магнитной связи будут наведенные сигналы (наводки) в цепи, подверженной влиянию. Устойчивость кабеля к наводкам характеризуется несколькими различными параметрами.
Переходное затухание на ближнем конце (Near End Cross Talk, NEXT) определяет устойчивость кабеля в том случае, когда наводка образуется в результате действия сигнала, генерируемого передатчиком, подключенным к одной из соседних пар на том же конце кабеля, на котором работает подключенный к подверженной влиянию паре приемник. Показатель NEXT, выраженный в децибелах, равен 10 lg Pвых/Pнав, где Pвых — мощность выходного сигнала, Pнав — мощность наведенного сигнала. Чем меньше значение NEXT, тем лучше кабель. Так, для витой пары Категории 5 показатель NEXT должен быть лучше -27 дБ на частоте 100 МГц.
Переходное затухание на дальнем конце (Far End Cross Talk, FEXT) описывает устойчивость кабеля к наводкам для случая, когда передатчик и приемник подключены к разным концам кабеля. Очевидно, что этот показатель должен быть лучше, чем NEXT, так как до дальнего конца кабеля сигнал приходит ослабленный вследствие затухания в каждой паре.
Показатели NEXT и FEXT обычно используются применительно к кабелю, состоящему из нескольких витых пар, когда взаимные наводки одной пары на другую могут достигать значительных величин. Для одинарного коаксиального кабеля (т. е. состоящего из одной экранированной жилы) подобный показатель не имеет смысла, не применяется он и для двойного коаксиального кабеля вследствие высокой степени защищенности каждой жилы. Оптические волокна также не создают сколько-нибудь заметных помех друг для друга.
В связи с тем, что в некоторых новых технологиях передача данных осуществляется одновременно по нескольким витым парам, в последнее время стали применяться суммарные показатели (PowerSUM, PS) — PS NEXT и PS FEXT. Они отражают устойчивость кабеля к суммарной мощности перекрестных наводок на одну из пар кабеля от всех остальных передающих пар.
Весьма важной характеристикой передающей среды является показатель защищенности кабеля (ACR), представляющий собой разность между уровнями полезного сигнала и помех. Чем больше это значение, тем с потенциально более высокой скоростью можно передавать данные по указанному кабелю.
ДОСТОВЕРНОСТЬ
Достоверность передачи данных характеризует вероятность искажения для каждого передаваемого бита данных. Иногда этот же показатель называют интенсивностью битовых ошибок (Bit Error Rate, BER). Величина BER для каналов связи без дополнительных средств защиты от ошибок (например, самокорректирующихся кодов или протоколов с повторной передачей искаженных кадров) составляет, как правило, 10-4—10-6, а в волоконно-оптических линиях связи — 10-9. Значение достоверности передачи данных, например в 10-4, говорит о том, что в среднем из 10000 бит неправильно интерпретируется значение одного бита.
Битовые ошибки происходят как из-за наличия помех на линии, так и по причине искажений формы сигнала вследствие ограниченной полосы пропускания линии. Поэтому для повышения достоверности передаваемых данных нужно повышать степень помехозащищенности линии, снижать уровень перекрестных наводок в кабеле, а также использовать линии связи с более широкой полосой рабочих частот.
ПОЛОСА ПРОПУСКАНИЯ
Полоса пропускания — еще одна вторичная характеристика. С одной стороны, она непосредственно зависит от затухания, а с другой — прямо влияет на такой важнейший показатель линии связи, как максимально возможная скорость передачи информации.
Полоса пропускания (bandwidth) — это непрерывный диапазон частот, для которого затухание не превышает заранее заданный определенный предел. Иными словами, полоса пропускания определяет диапазон частот синусоидального сигнала, при которых этот сигнал передается по линии связи без значительных искажений (часто за граничные принимаются частоты, где мощность выходного сигнала уменьшается в два раза по отношению к входному, что соответствует затуханию в -3 дБ). Как мы увидим ниже, ширина полосы пропускания в наибольшей степени влияет на максимально возможную скорость передачи информации по линии связи.
Таким образом, амплитудно-частотная характеристика, полоса пропускания и затухание являются универсальными характеристиками, и их знание позволяет сделать вывод о том, как через линию связи будут передаваться сигналы любой формы.
ПРОПУСКНАЯ СПОСОБНОСТЬ
Пропускная способность (количество бит информации, передаваемых в единицу времени) и достоверность передачи данных (вероятность доставки неискаженного бита или же вероятность его искажения) интересуют разработчиков компьютерной сети в первую очередь, поскольку эти характеристики прямо влияют на производительность и надежность создаваемой сети.
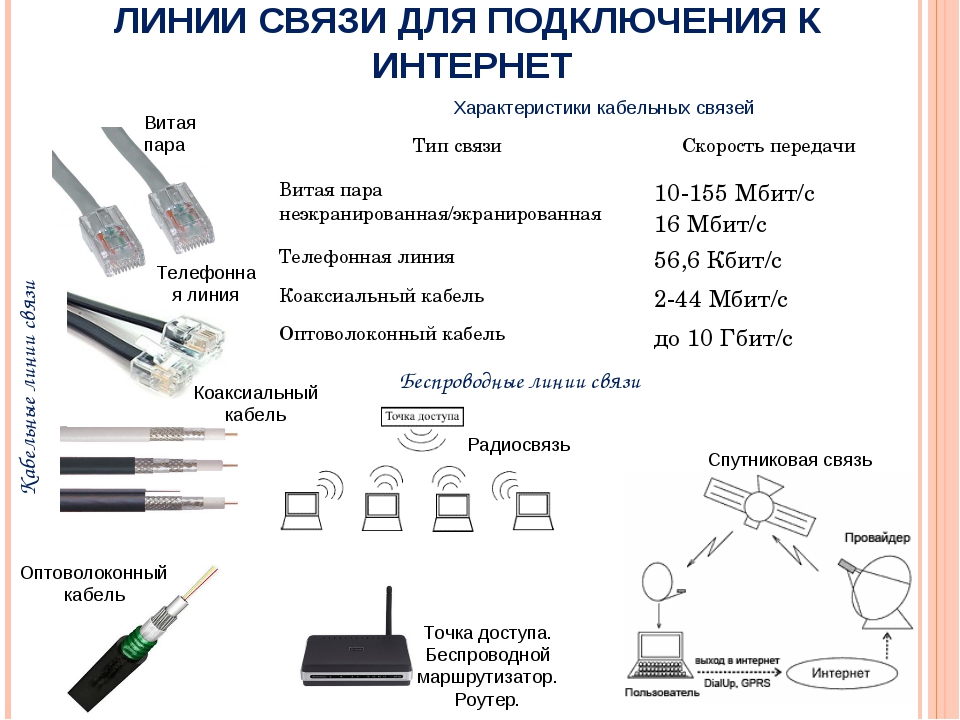
Пропускная способность и достоверность передачи данных зависят как от характеристик физической среды, так и от способа передачи данных. Следовательно, нельзя говорить о пропускной способности линии связи до определения протокола физического уровня. Пропускная способность (throughput) линии характеризует максимально возможную скорость передачи данных по линии связи. Она измеряется в битах в секунду (бит/c), а также в производных единицах — килобит в секунду (Кбит/c), мегабит в секунду (Мбит/с), гигабит в секунду (Гбит/с) и т. д.
Пропускная способность линий связи и коммуникационного сетевого оборудования традиционно измеряется в битах в секунду, а не в байтах в секунду. Это связано с тем, что данные в сетях передаются последовательно, т. е. побитно, а не параллельно, байтами, как это происходит между устройствами внутри компьютера. Такие единицы измерения, как килобит, мегабит или гигабит, в сетевых технологиях строго соответствуют степеням 10 (т. е. килобит — это 1000 бит, а мегабит — это 1000000 бит), как это принято во всех отраслях науки и техники, а не близким к этим числам степеням 2, как это принято в программировании, где приставка «кило» равна 210 = 1024, а «мега» — 220 = 1 048 576.
Пропускная способность линии связи зависит не только от ее характеристик, например от затухания и полосы пропускания, но и от спектра передаваемых сигналов. Если значимые гармоники сигнала (т. е. те гармоники, амплитуды которых вносят основной вклад в результирующий сигнал) не выходят за полосу пропускания линии, такой сигнал будет хорошо передаваться, и приемник сможет правильно распознать информацию, отправленную по линии передатчиком. Если же значимые гармоники выходят за границы полосы пропускания линии связи, то сигнал станет значительно искажаться, приемник — ошибаться при распознавании информации, а сама информация в конечном итоге не сможет передаваться с заданной пропускной способностью.
СПОСОБ КОДИРОВАНИЯ ИНФОРМАЦИИ
Выбор способа представления дискретной информации в виде подаваемых на линию связи сигналов называется физическим, или линейным, кодированием.
От выбранного способа кодирования зависят спектр сигналов и пропускная способность линии. Итак, разным способам кодирования может соответствовать разная пропускная способность. Например, витая пара Категории 3 способна передавать данные с пропускной способностью 10 Мбит/c при способе кодирования стандарта физического уровня 10BaseT и 33 Мбит/с при способе кодирования стандарта 100BaseT4.
Согласно теории информации, информацию несет лишь различимое и непредсказуемое изменение принимаемого сигнала. Таким образом, прием синусоиды, у которой амплитуда, фаза и частота остаются неизменными, информации не несет, так как изменение сигнала хотя и происходит, но легко предсказуемо. Аналогично, импульсы на тактовой шине компьютера не несут в себе информации, так как их изменения постоянны во времени. А вот импульсы на шине данных предсказать заранее нельзя, поэтому они переносят информацию между отдельными блоками или устройствами компьютера.
Большинство способов кодирования использует изменение какого-либо параметра периодического сигнала — частоты, амплитуды и фазы синусоиды или же знак потенциала последовательности импульсов. Периодический сигнал, параметры которого изменяются, называют несущим сигналом или несущей частотой, если в качестве такого сигнала применяется синусоида.
Если сигнал изменяется так, что различаются только два его состояния, то любое его изменение будет соответствовать наименьшей единице информации — биту. Если же сигнал может иметь более двух различимых состояний, то любое его изменение содержит несколько бит информации.
Количество изменений информационного параметра несущего периодического сигнала в секунду измеряется в бодах (baud). Период времени между соседними изменениями информационного сигнала называется тактом работы передатчика.
Пропускная способность линии в битах в секунду в общем случае не совпадает с числом бод. Она может быть как выше, так и ниже числа бод, и это соотношение зависит от способа кодирования.
Когда у сигнала более двух различимых состояний, пропускная способность в битах в секунду окажется выше, чем число бод. Например, если информационными параметрами являются фаза и амплитуда синусоиды (причем различаются четыре состояния фазы — в 00, 900, 1800 и 2700 и два значения амплитуды сигнала), то информационный сигнал может иметь восемь различимых состояний. В этом случае модем, работающий со скоростью 2400 бод (с тактовой частотой 2400 Гц), передает информацию со скоростью 7200 бит/с, так как при одном изменении сигнала передается три бита информации.
При использовании сигналов с двумя различимыми состояниями возможна обратная картина. Это часто происходит потому, что для надежного распознавания приемником пользовательской информации каждый бит в последовательности кодируется с помощью нескольких изменений информационного параметра несущего сигнала. Например, при кодировании единичного значения бит импульсом положительной полярности, а нулевого значения бит — импульсом отрицательной полярности физический сигнал дважды изменяет свое состояние при передаче каждого бит. При таком кодировании пропускная способность линии в два раза ниже, чем число бод, передаваемое по линии.
На пропускную способность линии оказывает влияние не только физическое, но и логическое кодирование. Выполняемое до физического кодирования, оно подразумевает замену бит исходной информации новой последовательностью бит, несущей ту же информацию, но обладающей, кроме этого, дополнительными свойствами, в частности возможностью для приемной стороны обнаруживать ошибки в принятых данных. Сопровождение каждого байта исходной информации одним битом четности — очень часто применяемый способ логического кодирования при передаче данных с помощью модемов. Другим примером логического кодирования может служить шифрация данных, обеспечивающая их конфиденциальность при передаче через общедоступные каналы связи. При логическом кодировании чаще всего исходная последовательность бит заменяется более длинной последовательностью, поэтому пропускная способность канала по отношению к полезной информации при этом уменьшается.
Наталья Олифер — обозреватель «Журнала сетевых решений/LAN». С ней можно связаться по адресу: [email protected]. Виктор Олифер — главный специалист «Корпорации Юни». С ним можно связаться по адресу: [email protected].
Поделитесь материалом с коллегами и друзьями
Первичные параметры линии
r0, Ом/км – продольное активное сопротивление на единицу длины линии
L0,Гн/км – продольная индуктивность на единицу длины линии.
g0, См/км – поперечная проводимость на единицу длины линии.
С0,Ф/км – поперечная емкость на единицу длины линии.
Длинная линия у которой первичные параметры одинаковы (постоянны) вдоль длины линии называется однородной.
Дифференциальные уравнения длинной линии
Рис. 10.2
Рассмотрим рисунок 10.2
x — расстояние от начала линии до произвольной ее точки (места наблюдения)
Напряжения и токи линии являются функциями двух независимых переменных:
— пространственной координаты х, определяющей место наблюдения.
— времени t , определяющей момент наблюдения.
Поэтому уравнения описывающие процессы в линии являются уравнениями частных производных.
Рис. 10.3
Выделим элементарный участок линии длиной Δх на расстоянии х от ее начала (рис. 10.3). Приближенно представим рассматриваемый элементарный участок в виде последовательно включенных сопротивления r0Δx и индуктивности
L0Δх и параллельно включенных проводимости g0Δх и емкости С0Δх.
Обозначим: U-напряжение между проводами в точке х.
ΔU- приращение напряжения на участке Δх
i-ток линии в точке х.
Δi- приращение тока на участке Δх.
Запишем уравнения по законам Кирхгофа для участка Δх.
Уменьшая Δх получим
— дифференциальные уравнения длинной линии (телеграфные уравнения)
Они могут быть решены при использовании начальных и граничных условий.
Решение уравнений однородной линии для установившегося синусоидального режима (рис. 10.5).
Рис. 10.5
Обозначим:
U1,U2 — комплексные действительные значения U и I в начале линии U2,I2 — комплексные действительные значения Uи I в конце линии.
U,I- комплексные действительные значения в точке х.
Пусть к линии приложено синусоидальное напряжение в установившемся режиме работы U и I в любой точке линии так же синусоидальны, а комплексы U и I зависят только от координаты х.
Перепишем телеграфные уравнения в комплексной форме.
Продифференцируем первое уравнение системы по х.
Обозначим: — коэффициент распространения
Тогда — линейное дифференциальное уравнение второго порядка.
Его решение:
p1 и р2 – корни характеристического уравнения.
Подставим полученное выражение в первое уравнение исходной системы.
Отсюда:
Обозначим: — волновое сопротивление.
Волновое сопротивление zc и коэффициент распространения γ называются вторичными параметрами длинной линии.
Для определения А1 и А2 будем использовать граничные условия.
Тогда перепишем полученные уравнения используя гиперболические функции.
При отсчете расстояния от конца линии получим:
Получим уравнения ЧП в форме А:
Поэтому γ длинной линии можно рассматривать как постоянную передачи ЧП замещающего линию длиной в 1 км.
Как всякий ЧП линия может быть представлена эквивалентной Т или П -образной схемой (рис. 10.6).
Рис. 10.6
Бегущие волны
Обозначим:
— прямая (падающая ) волна U.
Uм – действующее значение прямой волны линии.
Перейдем к мгновенному значению U падающей волны:
Если считать точку х фиксированной и рассматривать изменение U в ней в зависимости от времени, то оно представляет собой синусоидальную функцию с амплитудой постоянной. Если считать t – фиксированным и рассматривать изменение и вдоль линии ( в зависимости от х), то получим затухающую синусоидальную волну U , амплитуда которой уменьшается с ростом х. Изобразим прямые волны U соответствующие дум следующим друг за другом моментами времени t1 и t2 (рис. 10.7).
Рис. 10.7
Видно, что волна U перемещается от начала линии к концу.
Так как рассматриваемая волна перемещается от начала линии к концу, то она называется прямой (падающей). Убывание амплитуды волны обусловлено потерями в линии, а изменение фазы – конечной скоростью распространения электромагнитных колебаний.
Α — коэффициент затухания
Β — фазовый коэффициент.
Из уравнения (*) видно, что α характеризует изменение амплитуды волны на единицу длины линии, а β характеризует изменение фазы на единицу длины линии.
Под длиной волны λ понимаем расстояние между двумя точками линии в которых фазы бегущей волны различаются на 2π.
Под фазовой скоростью Vф понимаем скорость распространения точки фаза колебаний которой остается постоянной.
Аналогичное рассуждение можно сделать и для обратной волны U.
Обратные волны перемещаются от конца линии к началу (рис. 10.8).
Рис. 10.8
Обратные волны можно рассматривать как результат отражения прямых волн от конца линии (отраженные волны).
Рассмотрим выражение для тока
Отсюда видно что
Таким образом волновое сопротивление это отношение комплексного U к комплексному I бегущей волны (падающей или отраженной).
Первичный параметр — линия — Большая Энциклопедия Нефти и Газа, статья, страница 3
Первичный параметр — линия
Cтраница 3
Вторичными, или характеристическими, параметрами линии являются коэффициент затухания с, коэффициент фазы р и волновое сопротивление ZB, которые в свою очередь выражаются через первичные параметры линии и частоту. [31]
Характеристическими параметрами двухпроводной линии являются: емкость CD индуктивность Lx, активное сопротивление rt и утечка gi на единицу длины линии, представляющие собой так называемые первичные параметры линии. Однако более общими и более важными являются так называемые вторичные параметры, а именно: скорость распространения колебаний и, волновое сопротивление W, постоянная затухания ( 3, постоянная сдвига фаз а, постоянная распространения у ( 3 i а системы с распределенными постоянными. [32]
Вторичными, или характер и стически-м и, параметрами линии являются коэффициент ослабления, коэффициент фазы ( 3 и волновое сопротивление ZB, которые в свою очередь выражаются через первичные параметры линии и частоту. [33]
Из этого уравнения видно, что волновое сопротивление представляет собой комплексное число, модуль которого равен отношению модулей напряжения и тока в данной точке, а аргумент ср характеризует сдвиг фаз между векторами напряжения и тока ФвФи — ф / — Из уравнения (5.7) видно, что волновое сопротивление цепи зависит от первичных параметров линии и от частоты. [34]
Для количественной оценки распределенных параметров используют понятие первичных параметров длинной линии, которые равны значениям соответствующих распределенных параметров, измеренных на отрезке линии единичной длины. Эти первичные параметры линии показаны условно на рис. 7.2, а. Как видно из рисунка, погонные параметры LO и Ro относят не к двум, а к одному проходу длинной линии. [36]
Выражения (15.11) являются точными расчетными формулами, справедливыми для линий со сколь угодно значительными потерями. Они показывают, что аир зависят xai от первичных параметров линии, так и от угловой частоты генератора. [37]
Приемник представляет собой последовательное соединение линии без потерь, разомкнутой на конце, и активного сопротивления. Приемник подключен к источнику синусоидального напряжения. Первичные параметры линии: L 0 562 — 10 — 6 гн / км, С 10 — 4 фар / км, длина линии / 3 3 см; активное сопротивление равняется волновому сопротивлению. [38]
Приемник представляет собой последовательное соединение линии без потерь, разомкнутой на конце, и активного сопротивления. Приемник подключен к источнику синусоидального напряжения. Первичные параметры линии: L 0 562 10 — й гн / км, С — 10 — 4 фар / км, длина линии / — 3 3 см; активное сопротивление равняется волновому сопротивлению. [39]
Страницы: 1 2 3
Определение первичных параметров линии. Определение напряжения U1, тока I1, мощности в начале и конце линии, КПД линии
Исходные данные (16 вариант):
f = 10 кГц U2 = 50 В
l = 1 км Zн = 1400e—j7º Ом
a = 50 мм Тип – ВЛ
r = 0,4 мм
1. Определяем первичные параметры линии:
— сопротивление проводов двухпроводной медной линии на постоянном токе:
ρ – удельное сопротивление проводов при t=20º; для меди ρ=0,01785 Ом*мм2/м;
— поправочный коэффициент F(x), учитывающий увеличение активного сопротив ления за счёт поверхностного эффекта:
для меди µ=1;
По таблице определяем F(x):
; тогда
R0=r0(1+F(x))=71,12(1+3,2)=298,7 (Ом/км)
Индуктивность двухпроводной линии
;
.
Ёмкость двухпроводной воздушной линии на единицу длины:
Проводимость единицы длины линии:
G0=G’+nf=1×10-8+5×10-11×104=5,1×10-7 (См/км), где
G’ – проводимость изоляции на постоянном токе, равная 1×10-8 (См/км) при сухой погоде.
n – коэффициент диэлектрических потерь, равный 5×10-11 (См/км×Гц) при сухой погоде.
2. Определяем напряжение U1, ток I1, мощности в начале и конце линии, КПД линии
а) Определяем вторичные параметры линии:
— полное комплексное сопротивление единицы длины линии:
— полная комплексная проводимость единицы длины линии:
— волновое сопротивление линии:
— комплексный коэффициент распространения:
γl = αl+jβl = (0,195+j0,29)×1 = 0,195+j0,29
затухание сигнала αl = 0,195 (Нп)
изменение фазы βl = 0,29 (рад)
б) Запишем уравнения для линии с потерями через параметры конца линии:
Для расчёта напряжения и тока в начале линии U1и I1 вместо y подставляем l, тогда:
Так как ток I2 в конце линии неизвестен, но известны нагрузка и напряжение в конце линии, то найдём его:
Рассчитываем и , для этого воспользуемся следующими соотношениями:
; где
Рассчитаем U1 и I1 в начале линии:
в) Рассчитаем полную комплексную мощность в начале и конце линии и КПД линии
Полная мощность S1=2,464 (BA)
Активная мощность P1=2,34 (Вт)
Реактивная мощность Q1=-0,67 (вар)
Полная мощность S2=1,75 (BA)
Активная мощность P2=1,74 (Вт)
Реактивная мощность Q2=-0,21 (вар)
Определяем КПД линии:
η=(Р1/Р2)×100%=(1,74/2,34)×100%=74,36%
3. Для линии без потерь определяем напряжение U1 и ток I1 в начале линии, а также длину электромагнитной волны λ:
а) Для линии без потерь R0=0, G0=0
Нагрузка стала активной
Коэффициент фазы
Определяем изменение фазы сигнала по всей длине линии
Определяем волновое сопротивление
б) Напряжение и ток в начале линии без потерь
тогда
Длина электромагнитной волны λ:
4. Построим график U=f(βy) для линии без потерь:
|
0 |
2,16 |
|||
|
0 |
3,634 |
7,258 |
1 |
|
|
1 |
0 |
0,976 |
||
|
1 |
0,5 |
0 |
0,952 |
|
|
0 |
1 |
0,214 |
||
|
0 |
1 |
0,0458 |
||
|
0 |
0,084 |
0,1681 |
0,0077 |
|
|
50 |
38,21 |
20,5 |
48,98 |
Цепи с распределенными параметрами (Лекция №40)
В предыдущих лекциях рассматривались электрические цепи, геометрические размеры которых, а также входящих в них элементов не играли роли, т.е. электрические и магнитные поля были локализованы соответственно в пределах конденсатора и катушки индуктивности, а потери мощности – в резисторе. Однако на практике часто приходится иметь дело с цепями (линии электропередачи, передачи информации, обмотки электрических машин и аппаратов и т.д.), где электромагнитное поле и потери равномерно или неравномерно распределены вдоль всей цепи. В результате напряжения и токи на различных участках даже неразветвленной цепи отличаются друг от друга, т.е. являются функциями двух независимых переменных: времени t и пространственной координаты x. Такие цепи называются цепями с распределенными параметрами. Смысл данного названия заключается в том, что у цепей данного класса каждый бесконечно малый элемент их длины характеризуется сопротивлением, индуктивностью, а между проводами – соответственно емкостью и проводимостью.
Для оценки, к какому типу отнести цепь: с сосредоточенными или распределенными параметрами – следует сравнить ее длину l с длиной электромагнитной волны . Если , то линию следует рассматривать как цепь с распределенными параметрами. Например, для , т.е. при , и . Для , т.е. уже при к линии следует подходить как к цепи с распределенными параметрами.
Для исследования процессов в цепи с распределенными параметрами (другое название – длинная линия) введем дополнительное условие о равномерности распределения вдоль линии ее параметров: индуктивности, сопротивления, емкости и проводимости. Такую линию называют однородной. Линию с неравномерным распределением параметров часто можно разбить на однородные участки.
Уравнения однородной линии в стационарном режиме
Под первичными параметрами линии будем понимать сопротивление , индуктивность , проводимость и емкость , отнесенные к единице ее длины. Для получения уравнений однородной линии разобьем ее на отдельные участки бесконечно малой длины со структурой, показанной на рис. 1.
Пусть напряжение и ток в начале такого элементарного четырехполюсника равны u и i, а в конце соответственно и .
Разность напряжений в начале и конце участка определяется падением напряжения на резистивном и индуктивном элементах, а изменение тока на участке равно сумме токов утечки и смещения через проводимость и емкость. Таким образом, по законам Кирхгофа
или после сокращения на
| ; | (1) |
| . | (2) |
Теорию цепей с распределенными параметрами в установившихся режимах будем рассматривать для случая синусоидального тока. Тогда полученные соотношения при можно распространить и на цепи постоянного тока, а воспользовавшись разложением в ряд Фурье – на линии периодического несинусоидального тока.
Вводя комплексные величины и заменяя на , на основании (1) и (2) получаем
| ; | (3) |
| , | (4) |
где и — соответственно комплексные сопротивление и проводимость на единицу длины линии.
Продифференцировав (3) по х и подставив выражение из (4), запишем
.
Характеристическое уравнение
,
откуда
.
Таким образом,
| , | (5) |
где — постоянная распространения; — коэффициент затухания; — коэффициент фазы.
Для тока согласно уравнению (3) можно записать
| , | (6) |
где — волновое сопротивление.
Волновое сопротивление и постоянную распространения называют вторичными параметрами линии, которые характеризуют ее свойства как устройства для передачи энергии или информации.
Определяя и , на основании (5) запишем
| . | (7) |
Аналогичное уравнение согласно (6) можно записать для тока.
Слагаемые в правой части соотношения (7) можно трактовать как бегущие волны: первая движется и затухает в направлении возрастания х, вторая – убывания. Действительно, в фиксированный момент времени каждое из слагаемых представляет собой затухающую (вследствие потерь энергии) гармоническую функцию координаты х, а в фиксированной точке – синусоидальную функцию времени.
Волну, движущую от начала линии в сторону возрастания х, называют прямой, а движущуюся от конца линии в направлении убывания х – обратной.
На рис. 2 представлена затухающая синусоида прямой волны для моментов времени и . Перемещение волны характеризуется фазовой скоростью. Это скорость перемещения по линии неизменного фазового состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу волны:
| . | (8) |
Продифференцировав (8) по времени, получим
| . | (9) |
Длиной волны называется расстояние между двумя ее ближайшими точками, различающимися по фазе на рад. В соответствии с данным определением
,
откуда
и с учетом (9)
.
В соответствии с введенными понятиями прямой и обратной волн распределение напряжения вдоль линии в любой момент времени можно трактовать как результат наложения двух волн: прямой и обратной, — перемещающихся вдоль линии с одинаковой фазовой скоростью, но в противоположных направлениях:
| , | (10) |
где в соответствии с (5) и .
Представление напряжения в виде суммы прямой и обратной волн согласно (10) означает, что положительные направления напряжения для обеих волн выбраны одинаково: от верхнего провода к нижнему.
Аналогично для тока на основании (6) можно записать
| , | (11) |
где и .
Положительные направления прямой и обратной волн тока в соответствии с (11) различны: положительное направление прямой волны совпадает с положительным направлением тока (от начала к концу линии), а положительное направление обратной волны ему противоположно.
На основании (10) и (11) для прямых и обратных волн напряжения и тока выполняется закон Ома
Рассмотрим теоретически важный случай бесконечно длинной однородной линии.
Бесконечно длинная однородная линия. Согласованный режим работы
В случае бесконечно длинной линии в выражениях (5) и (6) для напряжения и тока слагаемые, содержащие , должны отсутствовать, т.к. стремление лишает эти составляющие физического смысла. Следовательно, в рассматриваемом случае . Таким образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны тока и напряжения. В соответствии с вышесказанным
| (12) |
На основании соотношений (12) можно сделать важный вывод, что для бесконечно длинной линии в любой ее точке, в том числе и на входе, отношение комплексов напряжения и тока есть постоянная величина, равная волновому сопротивлению:
.
Таким образом, если такую линию мысленно рассечь в любом месте и вместо откинутой бесконечно длинной части подключить сопротивление, численно равное волновому, то режим работы оставшегося участка конечной длины не изменится. Отсюда можно сделать два вывода:
Уравнения бесконечно длинной линии распространяются на линию конечной длины, нагруженную на сопротивление, равное волновому. В этом случае также имеют место только прямые волны напряжения и тока.
У линии, нагруженной на волновое сопротивление, входное сопротивление также равно волновому.
Режим работы длинной линии, нагруженной на сопротивление, равное волновому, называется согласованным, а сама линия называется линией с согласованной нагрузкой.
Отметим, что данный режим практически важен для передачи информации, поскольку характеризуется отсутствием отраженных (обратных) волн, обусловливающих помехи.
Согласованная нагрузка полностью поглощает мощность волны, достигшей конца линии. Эта мощность называется натуральной. Поскольку в любом сечении согласованной линии сопротивление равно волновому, угол сдвига между напряжением и током неизменен. Таким образом, если мощность, получаемая линией от генератора, равна , то мощность в конце линий длиной в данном случае
,
откуда КПД линии
и затухание
.
Как указывалось при рассмотрении четырехполюсников, единицей затухания является непер, соответствующий затуханию по мощности в раз, а по напряжению или току – в раз.
Литература
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- В чем заключается разница между цепями с сосредоточенными и распределенными параметрами?
- По какому критерию цепь относят к классу цепей с распределенными или сосредоточенными параметрами?
- Нарисуйте схему замещения длинной линии.
- Объясните понятия прямой и обратной бегущих волн.
- Что такое согласованный режим работы цепи с распределенными параметрами, чем он характеризуется?
- Определить первичные параметры линии, если ее вторичные параметры .
- Определить по условиям предыдущей задачи КПД линии длиной 200 км, считая, что она нагружена на сопротивление, равное волновому.
- Определить , и для кабеля, у которого , , если частота .
- По условиям предыдущей задачи определить длину волны и ее фазовую скорость.
Ответ:
Ответ: .
Ответ: ; ; .
Ответ:
энциклопедия киповца
Каждый бесконечно малый участок длинной линии - dx можно рассматривать как совокупность четырех элементов:
Ro- удельное сопротивление прямого и обратного проводов
Lo— удельная индуктивность петли образованная прямым и обратным проводом
Go— удельная проводимость , утечка между проводами.
Со— удельная емкость между проводами
Эти четыре составляющих называются первичными параметрами длинной линии.
Тогда длинную линию можно рассматривать как множество соединенных в цепочку бесконечно малых элементов dx, каждый из которых имеет сопротивление Rodx, индуктивность Lodx, проводимость Godx, емкость Codx.
Эквивалентная схема
х- координата (расстояние от начала линии до выбранного dx)
Е- источник
Z0- внутреннее сопротивление источника
Zн- сопротивление нагрузки
Такая система на основании второго закона Кирхгофа описывается следующей системой уравнений:
Преобразовав данную систему, пренебрегая при раскрытии скобок производными второго порядка, получим:
Эта система уравнений может быть использована на любом участке длинной линии при любом изменении ЭДС источника.
Рассмотрим установившийся режим длинной линии для источника переменного синусоидального напряжения:
, обозначим:
Zo = Ro+jwLo – комплексное сопротивление длинной линии
Yo = Go+jwCo – комплексная проводимость длинной линии
подставив производные из уравнения (*) в уравнение (**) , тогда получим:
Длинная линия характеризуется также двумя вторичными параметрами:
1) Волновое сопротивление
Волновое сопротивление зависит только от характера ЛС, от первичных параметров и от частоты и не зависит от длины кабеля. Волновое сопротивление или импеданс — это сопротивление, которое встречает электромагнитная волна при распространении вдоль любой однородной линии.
2) Затухание
Затухание измеряется в ДБ, бывает собственное и рабочее
Вследствии того что высокочастотные токи протекают ближе к поверхности проводника (поверхностный эффект) — на высоких частотах удельное сопротивление линии возрастает, а удельная индуктивность падает.
Наиболее выгодные условия прохождения сигнала по линии связи — когда цепь замкнута на согласованную нагрузку (ZH=W). В этом случае вся энергия сигнала поглощается приемником.
ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ КАБЕЛЬНЫХ ЛИНИЙ СВЯЗИ
ЛЕКЦИЯ 18. ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ КАБЕЛЬНЫХ ЛИНИЙ СВЯЗИ
Измерение Rшл, Rиз, С, Rасс. Измерительные приборы
ПЕРВИЧНЫЕ ПАРАМЕТРЫ ПЕРЕДАЧИ
Электрические свойства линий связи и качество передачи по ним полностью характеризуются первичными параметрами передачи: активным сопротивлением R, индуктивностью L, емкостью С, проводимостью изоляции G. Эти параметры не зависят от напряжения и передаваемого тока, а определяются лишь конструкцией линии, используемыми материалами и частотой тока.
По физической природе параметры линии аналогичны параметрам электрических контуров, составленных из элементов R, L, С. Разница лишь в том, что в контурах эти параметры являются сосредоточенными, а в линиях они равномерно распределены по всей их длине. Принято определять параметры линий связи на 1 км длины. На рис. 18.1 представлена эквивалентная схема участка цепи связи. Здесь включенные последовательно R и L (продольные) образуют суммарное сопротивление Z=R+jωL, a G и С (поперечные) суммарную проводимость Y=G+jωC.
Параметры R и L характеризуют процессы в металлических частях линии (проводники, экраны, оболочки), параметры G и С процессы в диэлектрике (изоляция кабеля, изоляторы воздушных линий).
При прохождении сигналов связи по линии уменьшаются напряжение и ток, так что мощность сигнала, проходящего в конец линии, существенно меньше начальной.
Рис. 18.1. Эквивалентная схема цепи связи
R и G обусловливают потери энергии: первый потери на тепло в проводниках и других металлических частях (экран, оболочка, броня), второй потери в изоляции. Если бы удалось создать линию с проводниками, обладающими сверхпроводимостью (R =0) и идеальной изоляцией (G=0), то передача электромагнитной энергии по такой линии проходила бы без потерь.
Активное сопротивление цепи R складывается из сопротивления проводников самой цепи и дополнительного сопротивления, обусловленного потерями в окружающих металлических частях кабеля (соседние проводники, экран, оболочка, броня). При расчете активного сопротивления обычно суммируются сопротивление цепи постоянному току (Ro) и переменному току (R~): R=Ro-R~.
Сопротивление цепи зависит от материала, диаметра, длины проводников и наличия окружающих металлических масс и измеряется в омах на километр (Ом/км).
Индуктивность цепи L обусловлена появлением (индуцированием) электродвижущей силы (ЭДС) при изменении магнитного потока. При этом индуцированная ЭДС может быть вызвана как изменением магнитного потока в соседней цепи (взаимоиндукция), так и в собственной цепи (самоиндукция) .
Индуктивность цепи складывается из внутренней индуктивности самих проводников и внешней индуктивности, обусловленной внешним магнитным потоком.
L=Lвт+Lвш
Индуктивность цепи зависит от материала, размеров проводников и расстояния между ними. С ростом частоты передаваемого тока уменьшается внутренняя индуктивность. Внешняя индуктивность остается постоянно:
Индуктивность измеряется в миллигенри на километр (мГн/км).
Емкость цепи С аналогична емкости конденсатора, у которого обкладками служат поверхности провод ков, а диэлектриком изоляционный материал. Емкость выражается отношением количества электричества напряжению: С= Q/U.
Емкость цепи зависит от диаметра проводников, расстояния между ми, свойств изоляционного матери и близости соседних металлических масс. Емкость практически постоянна в очень широком диапазоне частот
В кабельной технике емкость цепи принято называть рабочей емкостью в отличие от частичных емкостей, т.е. емкостей между любыми отдельными жилами и жилами оболочкой кабеля.
Емкость цепи измеряется в нанофарадах на км (нФ/км).
Проводимость изоляции G xapaктеризует качество изоляции проводников цепи (диэлектрик кабеля, материал изоляторов). Под проводимое изоляции понимается явление частичной электропроводимости изоляционных материалов, в результате часть передаваемой по цепи энергии рассеивается в диэлектрике, т. е. происходит утечка тока. Проводимость изоляции складывается из проводимостей изоляции постоянному (Go) и переменному току (G~): G=G0+ G~
Проводимость изоляции постоянному току обратно пропорциональна величине сопротивления изоляции (Rиз), Go=1/Rиз Проводимость изоляции переменному току растет с увеличением частоты и существенно зависит качества диэлектрика тангенс угла диэлектрических потерь (tg δ), т. е. G~=ωCtg δ
В результате проводимость изоляции определяется следующей формуле
Обычно величина GO=1/ Rиз мала, поскольку сопротивление изоляции нормируется 100010000 МОм-км. Проводимость изоляции измеряется сименсах на километр (См/км).
первичные параметры передачи (R, L, С, G) от диаметра и материала проводников, расстояния между ними, изоляции, частоты и температуры.
Вторичные ПАРАМЕТРЫ ПЕРЕДАЧИ
Вторичными параметрами линии являются волновое (характеристическое сопротивление Zв и коэффициент распространения γ. Они широко используются для оценки эксплуатации технических качеств линии связи. При проектировании, сооружений и эксплуатации кабельных магистралей в первую очередь нормируются и контролируются именно вторичные параметры линии.
Волновое сопротивление ZB это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, т. е. при условии отсутствия влияния на процесс передачи несогласованности нагрузок по концам линии. Волновое сопротивление свойственно данному типу кабеля и зависит лишь от его первичных параметров и частоты передаваемого тока.
Волновое сопротивление, Ом, рассчитывается по формуле
(4.14)
По своей физической природе величина ZB не зависит от длины кабельной линии и постоянна в любой точке цепи.
электромагнитная энергия, распространяясь вдоль кабельной линии, уменьшается по величине от начала к концу линии. Уменьшение или затухание энергии объясняется потерями ее в цепи передачи. Различают два вида потерь. Во-первых, потери её металлических элементах кабеля (токопроводящие жилы, экран, оболочка, броня). При прохождении тока по кабельной цепи происходит нагревание токопроводящих жил и других металлических элементов и создаются тепловые потери энергии. С ростом частоты эти потери увеличиваются: чем больше активное сопротивление цепи R, тем больше потери энергии в металлических элементах кабеля. Во-вторых, потери в изоляции (диэлектрике). Эти потери обусловлены несовершенством применяемых изоляционных материалов и затратами энергии на диэлектрическую поляризацию (G).
Потери в цепи передачи учитываются через коэффициент распространения у, который является комплексной величиной и может быть представлен суммой действительной и мнимой ее частей:
(4.15)
чем длиннее кабельная линия, тем больше изменяется передаваемая энергия (сигналы связи) по величине и фазе.
При передаче сигналов связи параметры α и β характеризуют соответственно затухание и изменение фаз тока, напряжения и мощности на участке кабельной цепи длиной 1 км и называются коэффициентом затухания и коэффициентом фазы.
Коэффициент распространения γ =α+jβ одновременно определяет изменение сигнала как по абсолютной величине, так и по фазе на 1 км длины кабеля.
Логарифмируя обе части приведенных выше выражений, получаем формулы для расчета затухания, дБ: αl = 20
al= (4.19)
Затухание в 1 дБ характеризует уменьшение по мощности в 1,26 раза, а по току или напряжению в 1,12 раза.
Между неперами и децибелами существует следующее соотношение: а (дБ) =20
Коэффициент фазы β измеряется в радианах или градусах на 1 км (1 рад = 57,3°).
Характер изменения тока вдоль однородной кабельной линии показан на рис. 4.4. Как видно из графика, вектор тока уменьшается и изменяет фазу вдоль линии. Уменьшение тока происходит по экспоненциальному закону (eαl)
Рассмотрим далее зависимость вторичных параметров кабельной линии частоты. Для упрощения анализа этой зависимости выразим вторичные параметры кабельных линий ZB и γ сокращенными формулами, которыми ;но пользоваться для расчетов.
При постоянном токе (f=0)
(4.20)
Следовательно, для данного случая коэффициент затухания α = , коэффициент фазы β = 0, а волновое сопротивление
В диапазоне низких частот (f ≈800 Гц) индуктивность кабельных цепей невелика, и можно пренебречь величиной ωL по сравнению с R.В этом случае можно также не считаться с параметром G по сравнению с ωС , т. е. в низкочастотном диапазоне — R > αL и G<ωС, тогда
Рис. 18.2. Изменение тока по амплитуде и фазе вдоль линии
Таким образом, (4.22)
В свою очередь
(4.23)
При высокочастотной передаче по кабельной цепи имеют место следующие соотношения:
Тогда, применив к выражению коэффициента распространения γ формулу бинома Ньютона и ограничившись лишь первыми двумя членами разложения, получим:
(4.24)
Волновое сопротивление в этом случае можно рассчитывать по формуле
(4.25)
Формулы (4.24) и (4.25) обеспечивают достаточную точность при расчетах, начиная примерно с f = 30:50 кГц. Для кабельных цепей с искусственно увеличенной индуктивностью эти же формулы справедливы и при более низких частотах. В этом случае условие реализуется за счет значительной величины индуктивности цепи.
Во всех остальных случаях расчет коэффициентов затухания и фазы, а также волнового сопротивления следует производить по полным формулам.
На рис. 4.5 приведена типовая частотная зависимость коэффициента затухания и коэффициента фазы кабельной цепи. Коэффициент затухания а, равный при постоянном токе вначале растет резко, а затем более плавно. Коэффициент фазы β растет от нуля почти по прямолинейному закону.
Характер частотной зависимости волнового сопротивления цепи кабеля иллюстрируется графиком, изображенным на рис. 4.6. Модуль волнового сопротивления с изменением частоты уменьшается от значения (при f = 0) до и сохраняет эту величину во всей области высоких частот. Угол волнового сопротивления равен нулю при постоянном токе (f = 0) и высоких частотах, а на частотах, близких к 800 Гц, имеет максимальное значение. В кабельных линиях угол всегда отрицателен и по абсолютной величине не превышает 45°, что свидетельствует о преобладании емкостной составляющей и емкостном характере волнового сопротивления кабелей.
Рис. 4.5. Частотная зависимость коэффициента затухания α и коэффициента фазы β кабельной цепи
Рис. 4.6. Частотная зависимость волнового сопротивления кабельной цепи
В качестве примера укажем, кабель с кордельно-бумажной из изоляцией и диаметром жилы d= 1,2 имеет волновое сопротивление 490< при f = 800 Гц и 175 е-4° при f= 60 000 Гц.
СКОРОСТЬ РАСПРОСТРАНЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ЭНЕРГИИ ПО ЦЕПЯМ СВЯЗИ
Электромагнитная энергия распространяется по линии с определенной скоростью. Посланный в линию сигнал достигает конца лишь через соответствующий промежуток времени. Скорость передачи зависит от параметров цепи и частоты тока. Она определяется из выражения υ= ω/β_ этой формулы видно, что скорость распространения является функцией частоты f= ω/2π и коэффициента фазы β, который в свою очередь зависит от первичных параметров линии. Таким образом, если затухание цепи α определяет качество и дальность связи, то коэффициент фазы β обусловливает скорость движения энергии линии.
В диапазоне высоких частот, когда скорость распространения электромагнитной энергии не зависит от частоты и определяется лишь параметрами кабеля:
υ= ω/β =1/√LC(4.26)
При постоянном токе
можно отметить, что с ростом частоты скоро распространения электромагнитной энергии по кабельным линиям существенно возрастает. Так, если при постоянном токе скорость распространение электромагнитной энергии по линии составляет примерно 10000 км/с, то при токах высоких частот она достигает величины порядка 200 000 км/с, приближаясь к скорости света (с = 300000 км/с).
ЭЛЕКТРИЧЕСКИЕ ПРОЦЕССЫ В СИММЕТРИЧНЫХ ЦЕПЯХ
Под действием переменного поля происходит перераспределение электромагнитной энергии по сечению жилы; при этом имеют место следующие явления: поверхностный эффект, эффект близости и воздействие на параметры цепи окружающих металлических масс (соседних токопроводящих жил, экрана, оболочки, брони). Эти явления вызывают изменения электромагнитного поля и параметров цепей. Активное сопротивление R и емкость С возрастают, а индуктивность L уменьшается. Наиболее существенно возрастает сопротивление цепи: R = Rо + Rп.э + Rбл + Rм, где Ro сопротивление постоянному току; R.э сопротивление за счет поверхностного эффекта; Rбл сопротивление за счет эффекта близости; RM сопротивление, обусловленное потерями в окружающих металлических массах.
Поверхностный эффект обусловлен действием электромагнитной волны, распространяющейся по токопроводящей жиле. Силовые линии внутреннего магнитного поля Н (рис. 4.8), пересекая толщу жилы, наводят в ней вихревые токи /в.т. направленные по закону Ленца, т. е. против вращения рукоятки при поступательном движении буравчика. Вихревые токи /вт в центре жилы имеют направление, обратное движению основного тока, протекающего по ней, а на периферии их направления совпадают.
В результате взаимодействия вихревых токов с основным происходит такое перераспределение тока по сечению жилы, при котором плотность его возрастает к поверхности жилы. Это явление носит название поверхностного эффекта. Последний возрастает с увеличением частоты тока, магнитной проницаемости, проводимости и диаметра жилы. При достаточно высокой частоте ток протекает лишь по поверхности жилы, что вызывает увеличение ее активного сопротивления.
Рис. 4.8. Явление поверхностного эффекта
Эффект близости возникает по причине взаимодействия внешних полей. Как, видно из рис. 4.9, внешнее магнитное поле Н проводника а, пересекая толщу проводника б, наводит в ней вихревые токи. На поверхности проводника б, обращенной к проводнику а, вихревые токи совпадают по направлению с протекающим по ней основным токам (/ + /в.т), а на противоположной поверхности жилы б они направлены навстречу основному току (//в.т)- Аналогичное перераспределение токов происходит в проводнике а.
Рис.4.9 Эффект близости проводников
При взаимодействии вихревых токов с основным плотность результирующего тока на обращенных друг к другу поверхностях токопроводящих проводников а и б увеличивается, а на отдельных уменьшается. Это явление («сближение» токов в проводниках а и б) носит название эффекта близости. Из-за этого неравномерного распределения плотности тока увеличивается активное сопротивление цепи переменному току.
Эффект близости также прямо пропорционален частоте, магнитной проводимости, проводимости и диаметр проводника и, кроме того, зависит расстояния между проводниками С приближением проводников к другу действие эффекта близости возрастает пропорционально квадрату расстояния. Если по двум соседним жилам токи проходят в одном направлении, то перераспределение их плотности из-за взаимодействия внешних электромагнитных полей приводит к увеличению плотности токов на взаимно отдаленных, поверхностях проводников а и б.
На рис. 4.10 показано распределение плотности токов в проводниках симметричной цепи, когда токи в них направлены противоположно (а) и когда они совпадают по направлению (б).
Рис. 4.10. Распределение плотности токов пары
Окружающие металлические массы за счет отражения от них электромагнитного поля также воздействуют на параметры цепи. Магнитное поле Н, создаваемое током, протекающим по жилам цепи, наводит вихревые токи /в.т в соседних цепях кабеля, в окружающем экране, металлической оболочке, броне и т. д. Вихревые токи нагревают металлические элементы кабеля и создают дополнительные тепловые потери энергии, что выражается как бы в «отсасывании» некоторой доли передаваемой энергии. При этом наиболее воздействуют близко расположенные к рассматриваемой цепи металлические элементы кабеля. Кроме того, вихревые токи создают поле обратного действия, которое воздействует на проводники цепи и также изменяет их параметры,
ПРОЦЕССЫ В ИЗОЛЯЦИИ
В отличие от токопроводящих жил, где имеются свободные электроны и действует ток проводимости /пр, в изоляционном материале нет свободных электронов, а имеются ионы и связанные диполи. Под действием переменного электромагнитного поля в изоляции происходит смещение диполей, их переориентация и поляризация (рис. 4.11). Поляризацией называется смещение положительных и отрицательных зарядов в изоляции под действием электрического поля.
Переменная поляризация обусловливает возникновение и действие токов смещения (емкостных токов) /См и вызывает затраты энергии на переориентацию диполей (потери в изоляционном материале диэлектрике). Чем выше частота колебаний, тем сильнее токи смещения и больше потери. При постоянном токе эти явления отсутствуют.
Явления в изоляции, как отмечалось выше, полностью характеризуются двумя параметрами: емкостью С, определяющей способность поляризации и величину токов смещения, и проводимостью изоляции G, определяющей величину потерь в изоляционном материале.
Рис. 4.11. Процесс поляризации: а) хаотическое расположение диполей; б) поляризация под действием электрического поля
ПЕРВИЧНЫЕ ПАРАМЕТРЫ СИММЕТРИЧНЫХ КАБЕЛЕЙ
Активное сопротивление симметричной кабельной цепи, Ом/км, состоит из сопротивления постоянному току Ro, сопротивления за счет поверхностного эффекта Rп.э, сопротивления за счет эффекта близости Rбл и сопротивления за счет потерь в окружающих металлических массах (соседние жилы, экран, броня) RM-
Сопротивление без учета потерь в металлических массах определяет по формуле:
R = Rо + Rп.э + Rбл + Rм (4.27)
Индуктивность, Гн/км, состоит из внешней и внутренней индуктивностей
(4.28)
Значения составляющих этой формулы приведены выше. Первая составляющая индуктивности превалирует над второй. С ростом частоты внутренняя индуктивность уменьшается.
Емкость, нФ/км, определяется по формуле
(4.29)
где ε эффективная диэлектрическая проницаемость изоляции;
ψ поправочный коэффициент, характеризующий близость металлических проводников. Расчетные формулы коэффициента фазы для парной и звездной скруток приведены ниже: скрутка парная
скрутка звездная
Проводимость изоляции, См/км, состоит из двух частей, обусловленных утечкой постоянного и переменного токов, и определяется формулой
G = Gо+ G~ = l/Rиз+ ωCtgδ. (4.30)
Здесь первый член Gо =l/Rиз учитывает утечку постоянного тока за счет несовершенства изоляции. Сопротивление изоляции Rиз составляет для городских телефонных кабелей 2000 МОм-км, а для кабелей дальней связи10000 МОм-км. Второй член учитывает утечку вследствие потерь в изоляции кабеля при переменном токе. Здесь tg δ тангенс угла диэлектрических потерь в изоляции кабеля.
В существующих кабелях второй член по абсолютной величине больше чем первый и проводимость изоляции можно рассчитывать по формуле G =ωСtgδ
Кабели связи имеют, как правило, сложную комбинированную изоляцию,
состоящую из твердого диэлектрика (стирофлекс, полиэтилен, фторопласт и др,) и воздуха. Результирующие эффективные значения диэлектрической проницаемости εэ и тангенса угла диэлектрических потерь tg δэ сложной изоляции определяются электрическими свойствами и соотношением объемов составных ее частей.
ОСНОВНЫЕ ЗАВИСИМОСТИ первичных ПАРАМЕТРОВ СИММЕТРИЧНЫХ ЦЕПЕЙ
Рассмотрим графики зависимости первичных параметров линий связи R, L, С, G от частоты, диаметра проводника и расстояния между проводками.
С увеличением частоты (рис. 4.12) значение параметров R и G возрастает за счет потерь в проводниках на вихревые токи и в изоляции на диэлектрическую поляризацию, а индуктивность L уменьшается, так как из-за поверхностного эффекта уменьшается внутренняя индуктивность проводника. Емкость С от частоты не зависит. При увеличении расстояния между проводниками (рис. 4.13) параметры R, С, G закономерно уменьшаются, а индуктивность L возрастает.
L.G.C
Рис. 4.12. Зависимость первичных параметров цепи от частоты
Рис. 4.13. Изменение первичных параметров цепи с увеличением расстояния между проводниками
Снижение R обусловлено уменьшением потерь на эффект близости. Рост L связан с увеличением площади контура, пронизываемого магнитным потоком. Емкость С уменьшается, так как проводники удаляются друг от друга и уменьшается их взаимодействие.
С увеличением диаметра проводников (рис. 4.14) параметры С и G растут, a L уменьшается. Изменение активного сопротивления имеет сложный характер. Это обусловлено тем, что с увеличением диаметра проводника сопротивление постоянному току резко уменьшается, а сопротивление за счет поверхностного эффекта и эффекта близости растет. Поэтому вначале R снижается резко, а затем снижение замедляется.
Теоретически от температуры зависят все четыре первичных параметра.
Рис. 4.14. Изменение первичных параметров цепи с увеличением диаметра проводников
Однако практически следует учитывать лишь температурную зависимость активного сопротивления. Изменение от температуры L, С, G весьма незначительно. Температурная зависимость активного сопротивления цепи определяется по формуле:
(4.35)
где Rt сопротивление при температуре t°С, R20 тоже при температуре 20°С; αR температурный коэффициент сопротивления, равный для меди 0,004 и для алюминия 0,0037.
С увеличением температуры сопротивление цепи растет (рис. 4.15). Физически это объясняется тем, что с увеличением температуры возрастает хаотическое движение атомов решетки и затрудняется прохождение электронов через нее.
Рис. 4.15. Зависимость электрического сопротивления от температуры
ВТОРИЧНЫЕ ПАРАМЕТРЫ СИММЕТРИЧНЫХ ЦЕПЕЙ
Вторичные параметры симметричных цепей ZB, α, β, υ следует рассчитывать по формулам, приведенным выше. В ряде случаев вторичные параметры выражают непосредственно через габаритные размеры цепей d, a и качество исходных материалов ε, tg δ.
Подставив в формулу ZB = YL/C значения L и С, получим значение волнового сопротивления симметричной цепи, Ом,
(4.36)
Коэффициент затухания симметричной цепи с медными проводника определится по формуле
α=
дБ/км, путем подстановки в нее значений первичных параметров:
(4.37)
Коэффициент фазы, рад/с, определится формулой
β = ω√LС или β = ω√ε/с, (4.3J
где с скорость света. Скорость распространения энергии , км/с.
(4.38)
Типовые частотные зависимости вторичных параметров цепи приведены на рис. 4.54.7.
КОАКСИАЛЬНЫЕ КАБЕЛИ СВЯЗИ
ЭЛЕКТРИЧЕСКИЕ ПРОЦЕССЫ В КОАКСИАЛЬНЫХ КАБЕЛЯХ
По коаксиальному кабелю можно передавать очень широкий спектр частот при малых потерях; этот кабель хорошо защищен от влияния соседних цепей и внешних помех. Кроме того, такая система связи в целом более экономична.
Взаимодействие электромагнитных полей внутреннего и внешнего проводников коаксиального кабеля таково, что его внешнее поле равно нулю. Это наглядно иллюстрируется на рис. 4.16, где показан характер изменения напряженности магнитного поля Hφa и Hφб каждого проводника (а и б) в отдельности. В металлической толще внутреннего проводника (а) магнитное поле Hφa возрастает, а вне его уменьшается по закону Hφa= , где r расстояние от центра провода до точки, в которой определяется напряженность поля. Поле Hφб внешнего проводника (б) изображено в соответствии с законом электротехники: внутри полого цилиндра магнитное поле отсутствует, а вне его выражается таким же уравнением, как и для сплошного проводника Hφб = //2πr, где r также расстояние от центра полого проводника. Поэтому при определении внешних магнитных полей проводов принимается одинаковым и исчисляется от их общего центра (нулевой точки).
Токи в проводниках а и б равны по величине и обратные по знаку, поэтому магнитные поля внутреннего и внешнего проводников Hφa и Hφб в любой точке пространства вне кабеля также равны по величине и направлены в разные стороны. Следовательно, результирующее магнитное поле вне кабеля
Таким образом, линии магнитного поля коаксиального кабеля располагаются в виде концентрических окружностей внутри него.
Электрическое поле также замыкается внутри коаксиального кабеля по радиальным направлениям между проводниками а и б. Поэтому в коаксиальном кабеле из-за отсутствия внешнего поля нет потерь в окружающих его металлических массах. Вся энергия распространяется только внутри кабеля и более эффективно передается по цепи.
На рис. 4.17 изображены электромагнитные поля коаксиальной и симметричной цепей. Как видно из рисунка, электромагнитное поле коаксиальной цепи полностью замыкается внутри нее, а силовые линии электромагнитного поля симметричной цепи действуют на довольно значительном от нее расстоянии. Отсутствие внешнего электромагнитного поля обусловливает основные достоинства коаксиальных кабелей: широкий диапазон частот, большое число каналов, защищенность от помех и возможность организации однокабельной связи. В симметричных цепях из-за наличия внешнего электромагнитного поля возникают вихревые токи в соседних цепях и окружающих металлических массах (оболочка, экран), часть энергии рассеивается в виде потерь на тепло и увеличивается затухание. Кроме того, в симметричных кабелях за счет внешнего поля наводятся помехи в соседних цепях.
Рис. 4.16. Результирующее магнитное поле коаксиальной цепи и его составляющие
Рис. 4.17. Электромагнитное поле цепи: а) симметричной; б) коаксиальной
Рассмотрим действие поверхностного эффекта и эффекта близости в коаксиальных кабелях и определим характер распределения плотности токов в проводах при различных частотах.
Распределение плотности тока в проводе а определяется действием поверхностного эффекта (рис. 4.8). Перераспределение плотности тока по сечению проводника б обусловлено эффектом близости к нему проводника а.
На рис. 4.18 показано переменное магнитное поле, создаваемое током проводника а, которое наводит в металлической толще полого проводника б вихревые токи (/в.т)- На внутренней поверхности проводника б направления вихревых и основного токов совпадают (/ + /в.т), а на наружной поверхности они противоположны (//в.т). В результате ток в проводнике б перераспределяется так, что его плотность возрастает в направлении к внутренней поверхности.
Следовательно, токи в проводниках а и б коаксиальной цепи как бы смещаются и концентрируются на взаимно обращенных поверхностях проводников (рис. 4.19). Чем выше частота тока, тем сильнее эффект смещения тока на внешнюю поверхность проводника а и внутреннюю поверхность проводника б. Энергия как бы вытесняется из металлической толщи проводников и сосредоточивается внутри коаксиального кабеля, в изоляции , а проводники задают лишь направление распространению волн электромагнитной энергии.
Мешающее электромагнитное поле высокой частоты, создаваемое соседними цепями передачи или другими источниками помех, действуя на внешний проводник б (оболочку) коаксиальной цепи, распространяется не по всему сечению кабеля, а лишь по наружной его поверхности.
Таким образом, внешний проводник б коаксиального кабеля защищает (экранирует) передачу, ведущуюся по кабелю, мешающих влияний.
Рис. 4.18. Распределение плотности тока во внешнем проводнике
Из рис. 4.20 видно, что основной ток передачи (рабочий ток) концентрируется на внутренней поверхности проводника б коаксиального кабеля, ток помех на наружной стороне этого проводника. Основной ток и ток помех проникают в толщу проводника лишь на глубину, определяемую коэффициентом вихревых токов. При этом чем выше частота, тем больше отдаляются друг от друга основной к и ток помех, и, следовательно, бель лучше защищен от действия сторонних помех. Таким образом, отличие от всех других типов кабелей в коаксиальных кабелях на высокиx частотах защита от помех обеспечивается их конструкцией.
Рис. 4.19. Концентрация токов на взаимно обращенных друг к другу поверхностях внутреннего (а) и внешнего (б) проводников коаксиальной цепи.
ПЕРВИЧНЫЕ ПАРАМЕТРЫ КОАКСИАЛЬНЫХ КАБЕЛЕЙ
В области высоких частот (свыше ) кГц), для которых используется коаксиальный кабель, первичные параметры могут быть определены по бедующим формулам. Активное сопротивление, Ом/км,
(4.40)
где k= коэффициент вихревых токов; апроводимость; rа и rb радиусы внутреннего и внешнего проводников. Для медных проводников
Для алюминиевых проводников
Если внутренний проводник медный, а внешний алюминиевый,
Из приведенных формул следует, что при применении обоих алюминиевых проводников вместо медных сопротивление возрастает на 29%, а при замене меди на алюминий только у внешнего проводника сопротивление возрастает всего на 6%.
Индуктивность, Гн/км,
(4.41)
Для медных проводников
Для алюминиевых проводников
Если внутренний проводник медный, а внешний алюминиевый,
В области высоких частот результирующая индуктивность определяется в основном внешней индуктивностью L = Lвш = 21n(rb/ra)10-4, поэтому замена меди на алюминий мало изменяет величину индуктивности кабельной цепи.
Емкость, нФ/км,
(4.42)
Здесь εэ эффективное значение диэлектрической проницаемости.
Проводимость изоляции, См/км,
(4.43)
где tg δ3 тангенс угла диэлектрических потерь; Rиз сопротивление изоляции, равное 10000 МОм-км. В области высоких частот, используемых для коаксиальных кабелей, величиной Go можно пренебречь и G = ωCtg δэ.
Значения эффективной диэлектрической проницаемости еэ и тангенса угла диэлектрических потерь tg δэ комбинированной изоляции, применяемой в коаксиальных кабелях, приведены в табл. 4.5. Там же даны соотношения объемов диэлектрика Vд и воздуха Vв.
ОСОБЕННОСТИ РАСЧЕТА ВТОРИЧНЫХ ПАРАМЕТРОВ КОАКСИАЛЬНЫХ КАБЕЛЕЙ
Коаксиальные кабели практически используются в спектре от 60 кГц выше, где R< ωL и G< ωС, поэтом вторичные параметры можно рассчитывать по формулам:
коэффициент затухания, Нп/км,
коэффициент фазы, рад/км,
волновое сопротивление, Ом,
скорость распространения, км/с,
Однако эти параметры целесообразно выражать непосредственно через габаритные размеры (d и D) и xapaктеристики изоляции (ε и tg δ).
Коэффициент затухания а, дБ/км при подстановке в формулу α= αм + αд первичных параметров и проведении соответствующих преобразований дл кабеля с медными проводниками определяется выражением
Из формулы видно, что потери в металлических элементах коаксиальной цепи (первый член) изменяются пропорционально √ f, а потери в изоляции (второй член) связаны с частоте линейным законом и с увеличение f возрастают значительно быстрее (рис. 4.21).
При использовании высококачественных изоляционных материалов (с малым
tg δ) можно добиться определенном частотном диапазоне малых диэлектрических потерь и положить αд = 0; при более высоких частотах они настолько возрастают, что причина αд играет доминирующую роль в общем затухании кабеля, практически используемом спектре тот передачи по коаксиальным кабелям (до 60-106 Гц) при современных( изоляционных материалах величина αд незначительна и затухание увеличивается примерно пропорционально √ f.
Рис. 4.21. Частотная зависимость составляющая затухания в металле (αм) и в диэлектрике (αд)
При замене медных проводников алюминиевые затухание возрастает пропорционально соотношению активных сопротивлений или соответственно обратно пропорционально корню квадратному из проводимостей металлов αа/αм =
, т. е. Затухания коаксиального кабеля с алюминиевыми проводниками больше, чем с медными на 29%.
При соотношении радиусов проводников rb/ra = 3,6 получим —- = =
ам Ни
= 1,06, т. е. затухание кабеля возрастает всего на 6%. Изложенное дает основание сделать вывод о целесообразности применения коаксиальных кабелей с внешними алюминиевыми проводниками. При этом расход меди на изготовление коаксиального кабеля сокращается на 65%.
Коэффициент фазы β, рад/км, коаксиальной цепи определяется из уравнения
Однако его можно выразить и таким образом:
(4.44)
где с скорость света.
Скорость распространения v, км/с, электромагнитной энергии по коаксиальным цепям
(4.45)
коэффициент фазы с увеличением частоты возрастает прямолинейно. Это обусловливает почти полное постоянство скорости передачи энергии по коаксиальному кабелю во всем рассматриваемом спектре частот. Скорость передачи уменьшается с увеличением диэлектрической проницаемости е. Скорость передачи энергии по коаксиальным кабелям выше, чем по кабелям других типов, и приближается к скорости распространения электромагнитных волн в воздухе, т. е. к скорости света.
Волновое сопротивление ZB, Ом, коаксиальной цепи определяется по формуле
(4.46)
В кабелях со сплошной изоляцией (ε = 2,3) ZB = 50 Ом, а в кабелях с комбинированной изоляцией (ε = 1,1) волновое сопротивление составляет примерно 75 Ом.
Частотная зависимость волнового сопротивления в спектре от 60 кГц и выше весьма незначительна, и волновое сопротивление можно считать постоянной величиной.
PAGE 9
Постоянная распределенной линии
Константы первичной линии — это параметры, которые описывают характеристики линий передачи из меди (или другого проводящего материала) с точки зрения физических электрических свойств линии. Константы первичной линии относятся только к медным линиям и должны быть противопоставлены константам вторичной линии, которые могут быть получены из них и более широко применимы. Константы вторичной линии могут использоваться, например, для сравнения характеристик волновода с медной линией, в то время как первичные константы не имеют значения для волновода.
Константа первичной линии
Эквивалентная схема
Постоянная распределенной или первичной линии-
Индуктивность
Когда к линии передачи подается переменный ток, ее индуктивное реактивное сопротивление (XL) увеличивается с увеличением частоты. Поскольку линия передачи состоит из миллионов мелких частиц, цепочка этих частиц заставляет линию передачи вести себя как индуктор.
Наличие этой индуктивности дает нам сопротивление протеканию переменного тока.Эта индуктивность также является одной из постоянных первичной линии и измеряется в Гн / км Генри / километр.
-
Емкость
Поскольку линия передачи состоит из двух проводников и между ними присутствует диэлектрик, очевидно, что в линиях передачи будет присутствовать емкость. Диэлектрическим материалом, используемым в линиях передачи, может быть воздух, пластик, резина, полистирол или полиэтилен и т. Д. Емкость линии передачи измеряется в ф / км.
-
Проводимость
Два провода линии передачи отделены друг от друга с помощью изоляционного материала. Поскольку каждый изолирующий материал имеет более или менее проводящий эффект, поэтому проводимость также является одной из констант первичной линии. Он измеряется в МО / км.
-
Сопротивление
Поскольку линия передачи сделана из токопроводящего провода, и мы знаем, что каждый провод имеет определенное сопротивление в зависимости от типа используемого материала.Линия передачи также будет иметь сопротивление контура, которое известно как одна из постоянных первичной линии. Измеряется в Ом / км.
Импеданс или характеристики Импеданс Z
oЕсли линия передачи сделана бесконечной и мы измеряем ее входное сопротивление от источника, это входное сопротивление бесконечно длинной линии передачи известно как ее характеристическое сопротивление. Он обозначается аббревиатурой Z o . Он также известен как импульсное сопротивление.
Формула для перенапряжения или характеристического импеданса Z
oДля измерения импеданса линии передачи используются следующие формулы.
-
Здесь L означает индуктивность на единицу длины линии передачи. C означает емкость на единицу длины линии передачи.
-
Здесь Z означает полное сопротивление линии передачи, а y означает полное сопротивление линии передачи. (Полное сопротивление противоположно импедансу)
-
При условии, что линия передачи бесконечна.
-
J обозначает разность углов или разность размеров
W обозначает 2πf
G обозначает проводимость
Какие параметры линии передачи?
Линия передачи имеет в основном четыре параметра : : сопротивление, индуктивность, емкость и шунтирующую проводимость. Эти параметры равномерно распределены по линии . ЭДС создает в линии передачи , сопротивляясь протеканию тока в проводнике, и этот параметр известен как индуктивность линии .
Щелкните, чтобы увидеть полный ответ
Тогда каковы основные компоненты линий передачи средней и большой протяженности?
Линии передачи состоят из различных компонентов , а именно опор, решетчатых конструкций, проводов, кабелей, изоляторов, фундаментов и систем заземления. Эти компоненты описаны более подробно в этом документе. Основные функции линии передачи Структуры — обеспечивать механическую опору для проводников.
Кроме того, почему параметры линии называются распределенными элементами? Из-за эффекта времени прохождения нельзя предположить, что вся индуктивность или емкость линии находится в определенной точке пространства. Индуктивность и емкость распределены по по длине линии . Таким образом, это , называемое , «Распределенные параметры » строки .
Также спрашивают, какое сопротивление линии передачи?
Что касается источника V (0, t), линия передачи ведет себя точно так же, как резистор номиналом √ (L / C).Мы называем это сопротивление характеристическим сопротивлением линии передачи . Характеристический импеданс свободного пространства для волн, распространяющихся в вакууме, составляет 377 Ом.
Какие бывают типы линий передачи?
Типы линий передачи включают параллельную линию (лестничная линия, витая пара), коаксиальный кабель и плоские линии передачи, такие как полосковые и микрополосковые. Чем выше частота электромагнитных волн, движущихся по данному кабелю , или среде, тем короче длина волны.
Вопросы и ответы по основным параметрам линии передачи
Этот набор вопросов и ответов с множественным выбором (MCQ) по теории электромагнитной теории посвящен «Первичным параметрам линии передачи».
1. Какой из следующих параметров не является основным?
a) Сопротивление
b) Константа затухания
c) Емкость
d) Проводимость
Посмотреть ответ
Ответ: b
Объяснение: Основными параметрами линии передачи являются сопротивление, индуктивность, емкость и проводимость.Затухание, фаза и постоянная распространения являются второстепенными параметрами. Таким образом, нечетной является константа затухания.
2. Сети, в которых параметры R, L, C индивидуально сконцентрированы или сосредоточены в дискретных точках цепи, называются
a) сосредоточенными
b) распределенными
c) параллельными
d) парными
Просмотреть ответ
Ответ: a
Объяснение: Сети, в которых параметры R, L, C сконцентрированы по отдельности или сосредоточены в дискретных точках цепи, называются сетями с сосредоточенными параметрами.Эти сети можно определенно идентифицировать как представляющие определенный параметр. Примером могут служить фильтры.
3. Линии, имеющие R, L, C, распределенные по цепи, называются
a) Сосредоточенные
b) Распределенные
c) Параллельные
d) Парные
Просмотр ответа
Ответ: b
Пояснение: В распределенных линиях первичный параметры распределяются по цепи, причем каждая длина элемента имеет свои собственные значения, и концентрация отдельных параметров невозможна.Пример — передача энергии.
4. Какой первичный параметр равномерно распределен по длине проводника?
a) G
b) C
c) L
d) R
Посмотреть ответ
Ответ: d
Пояснение: Сопротивление — это первичный параметр, который равномерно распределен по длине проводника. Это зависит от площади сечения и длины проводника.
5. Первичный параметр, связанный с магнитным потокосцеплением, —
a) R
b) L
c) C
d) G
Просмотр ответа
Ответ: b
Пояснение: Когда проводники пропускают ток, проводник будут окружены и связаны магнитным потоком.Потоковые связи на ампер тока вызывают эффект индуктивности. Обозначается L.
6. Основным параметром, связанным с электрическими зарядами, является
a) G
b) R
c) C
d) L
Просмотр ответа
Ответ: c
Пояснение: проводники разделены изолирующими диэлектриками для хранения электрические заряды, вызывает эффект емкости. Емкость распределена по всей длине проводника.
7.Ток утечки в линиях передачи обозначается как
a) Сопротивление
b) Излучение
c) Проводимость
d) Поляризация
Посмотреть ответ
Ответ: c
Объяснение: Диэлектрики или изоляторы открытой проводной линии не могут быть безупречным, и будет течь ток утечки. Эта проводимость утечки существует между проводниками.
8. Найдите полное сопротивление линии передачи, имеющей напряжение 24 В и ток проводимости 1,2 А, составляет
a) 25.2
b) 22,8
c) 28,8
d) 20
Посмотреть ответ
Ответ: d
Пояснение: По закону Ома импеданс — это отношение напряжения к току. Подставляя V = 24 и I = 1,2, получаем Z = V / I = 24 / 1,2 = 20 единиц.
9. Характеристическое сопротивление линии передачи с полным сопротивлением и полной проводимостью 16 и 9 соответственно составляет
a) 25
b) 1,33
c) 7
d) 0,75
Посмотреть ответ
Ответ: b
Пояснение: Характеристическое сопротивление задается формулой Zo = √ (Z / Y), где Z — полное сопротивление, а Y — полная проводимость.Подставив Z = 16 и Y = 9, мы получим характеристический импеданс как √ (16/9) = 1,33 единицы.
10. Константа распространения линии передачи с полным сопротивлением 9 и 16 соответственно составляет
a) 25
b) 144
c) 12
d) 7
Посмотреть ответ
Ответ: c
Объяснение: Постоянная распространения задается формулой γ = √ (ZY), где Z равно 9, а Y равно 16. При подстановке данных значений постоянная распространения будет равна γ = √ (ZY) = √ (9 x 16) = 12 единиц.
11. Найдите выражение характеристического импеданса через параметры индуктивности и емкости.
a) Zo = √ (LC)
b) Zo = LC
c) Zo = √ (L / C)
d) Zo = L / C
Посмотреть ответ
Ответ: c
Пояснение: дано характеристическое сопротивление на квадратный корень из отношения индуктивности к емкости. Таким образом, Zo = √ (L / C) является искомым выражением.
12. Когда линия передачи имеет импеданс нагрузки, такой же, как у характеристического импеданса, линия называется
a) Параллельная
b) Перпендикулярная
c) Поляризованная
d) Соответствующая
Посмотреть ответ
Ответ: d
Объяснение: Когда полное сопротивление нагрузки линии передачи такое же, как и характеристическое сопротивление, линия считается согласованной.В таких случаях произойдет полная передача мощности с минимальными потерями.
Sanfoundry Global Education & Learning Series — Электромагнитная теория.
Чтобы практиковать все области электромагнитной теории, представляет собой полный набор из 1000+ вопросов и ответов с множественным выбором .
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Процесс изготовления коаксиальных кабелей, основные параметры.
Чтобы обеспечить максимальную производительность, коаксиальные кабели должны изготавливаться в соответствии с процессом проектирования высокого качества. Кроме того, существует ряд параметров, которые необходимо учитывать в процессе производства . Основные из них перечислены ниже:
- Характеристическое сопротивление «Z o »
- Емкость «C»
- Затухание «α»
- Номинальная мощность
- Скорость распространения «Вп»
В частности, в высокочастотных системах передачи важно, чтобы характеристическое сопротивление «Z o », выраженное в Ом, соответствовало сопротивлению приемной системы.Любая разница характеристического импеданса на переходе существенно повлияет на качество сигнала. Точно так же на искажения и потери сигнала может влиять непостоянство качества проводника, геометрии кабеля и диэлектрической однородности.
Емкость «C», измеряемая в Фарадах, важна для понимания емкости диэлектрического материала в проводниках с разностью потенциалов для сохранения диэлектрического заряда. Кабели с низкой емкостью больше подходят для линий передачи данных, так что они делают возможной передачу на большие расстояния.Чтобы сохранить эту особенность, используемый материал имеет низкую диэлектрическую проницаемость, например полипропилен.
Затухание «α», измеряемое в дБ, необходимо, поскольку оно определяет уровень передачи линии . Это соотношение входного и выходного напряжения. Затухание Результатом являются потери напряжения сигнала и замедление импульса. Два фактора, вызывающие затухание:
- Потери сопротивления в проводниках
- Потери в диэлектрике
Нагрев и размягчение диэлектрика влияет на номинальную передаваемую мощность.Фактически, потери тепла прямо пропорциональны частоте, диэлектрической проницаемости и коэффициентам рассеяния. Таким образом, номинальная мощность зависит от 3 элементов:
- Размер кабеля
- Температура окружающей среды
- Отражение напряжения
Скорость распространения «Vp», измеренная в процентах, представляет период, необходимый сигналу для прохождения через линию передачи.
Следовательно, процесс производства коаксиальных кабелей приблизительно вызовет размерные неровности или неоднородности материала вдоль линии и, следовательно, повлияет на импеданс элемента.Часть сигнала будет потеряна при каждом отклонении импеданса. Отражения усиливаются с увеличением частоты.
В кабельной промышленности равномерность возвратных потерь используется в качестве индикатора для оценки качества кабеля.
Однако рынок предпочитает использовать структурный возврат убытков (SRL). Таким образом, этапы производства чрезвычайно важны для конечного качества продукта. Необходимо учитывать множество параметров и элементов, это лишь некоторые из них.Однако их описание указывает на важность выбора поставщика экструзионных линий , который хорошо знает предмет и имеет обширный опыт.
11. Вопросы и ответы по линиям передачи
Вопросы и ответы по основным параметрам линии передачи — Sanfoundry by staff10 Этот набор электромагнитной теории Mu
Просмотры 339 Загрузки 21 Размер файла 376KB
Отчет DMCA / Авторское право
СКАЧАТЬ ФАЙЛ
Рекомендовать истории
Предварительный просмотр цитирования
Вопросы и ответы по первичным параметрам линии передачи — Sanfoundry by staff10 В этом наборе вопросов и ответов с множественным выбором (MCQ) по теории электромагнитного поля основное внимание уделяется «Первичным параметрам линии передачи».1. Какой из следующих параметров не является основным? a) Сопротивление b) Постоянная затухания c) Емкость d) Вид проводимости. Просмотр Ответ: b Пояснение: Основными параметрами линии передачи являются сопротивление, индуктивность, емкость и проводимость. Затухание, фаза и постоянная распространения являются второстепенными параметрами. Таким образом, нечетной является константа затухания. 2. Сети, в которых параметры R, L, C сконцентрированы по отдельности или сосредоточены в дискретных точках цепи, называются a) сосредоточенными b) распределенными c) параллельными d) парным представлением. Ответ Ответ: a Объяснение: Сети, в которых Параметры R, L, C индивидуально сконцентрированы или сосредоточены в дискретных точках цепи, которые называются сосредоточенными сетями.Эти сети можно определенно идентифицировать как представляющие определенный параметр. Примером могут служить фильтры. 3. Линии, в которых R, L, C распределены по цепи, называются a) сосредоточенными b) распределенными c) параллельными d) парным представлением Ответ Ответ: b Объяснение: В распределенных линиях основные параметры распределены по цепи с каждым элементом. длина, имеющая свои значения и концентрация отдельных параметров невозможна. Пример — передача энергии.
4.Какой первичный параметр равномерно распределен по длине проводника? a) G b) C c) L d) R Просмотр Ответ: d Пояснение: сопротивление — это первичный параметр, который равномерно распределен по длине проводника. Это зависит от площади сечения и длины проводника. 5. Первичный параметр, связанный с магнитной связью: a) R b) L c) C d) G Просмотр Ответ: b Объяснение: Когда проводники пропускают ток, проводник будет окружен и связан магнитным потоком.Потоковые связи на ампер тока вызывают эффект индуктивности. Он обозначается L. 6. Первичный параметр, связанный с электрическими зарядами: a) G b) R c) C d) L Просмотр Ответ Ответ: c Пояснение: проводники разделены изолирующими диэлектриками для хранения электрических зарядов. вызывает эффект емкости. Емкость распределена по всей длине проводника. 7. Ток утечки в линиях передачи называется a) сопротивлением b) излучением c) проводимостью d) поляризационным обзором Ответ Ответ: c Объяснение: диэлектрики или изоляторы разомкнутой проводной линии могут быть несовершенными, и ток утечки потечет.Эта проводимость утечки существует между проводниками.
8. Найдите принимающее сопротивление линии передачи с напряжением 24 В и током проводимости 1,2 А: a) 25,2 b) 22,8 c) 28,8 d) 20 Просмотр ответа Ответ: d Пояснение: По закону Ома импеданс это отношение напряжения к току. Подставляя V = 24 и I = 1,2, получаем Z = V / I = 24 / 1,2 = 20 единиц. 9. Характеристическое сопротивление линии передачи с полным сопротивлением и проводимостью 16 и 9 соответственно равно a) 25 b) 1.33 c) 7 d) 0,75 Просмотр ответа Ответ: b Пояснение: Характеристическое сопротивление определяется выражением Zo = √ (Z / Y), где Z — полное сопротивление, а Y — проводимость. Подставив Z = 16 и Y = 9, мы получим характеристический импеданс как √ (16/9) = 1,33 единицы. 10. Константа распространения линии передачи с импедансом и проводимостью 9 и 16 соответственно равна a) 25 b) 144 c) 12 d) 7 Посмотреть ответ Ответ: c Пояснение: Постоянная распространения определяется выражением γ = √ (ZY) , где Z равно 9, а Y равно 16.При подстановке данных значений постоянная распространения будет равна γ = √ (ZY) = √ (9 x 16) = 12 единиц. 11. Найдите выражение характеристического импеданса через параметры индуктивности и емкости. a) Zo = √ (LC) b) Zo = LC c) Zo = √ (L / C) d) Zo = L / C Посмотреть ответ
Ответ: c Пояснение: характеристическое сопротивление дается квадратным корнем из отношение индуктивности к емкости. Таким образом, Zo = √ (L / C) является искомым выражением. 12. Когда линия передачи имеет сопротивление нагрузки, такое же, как у характеристического импеданса, линия называется а) параллельной б) перпендикулярной в) поляризованной г) согласованной точки зрения Ответ Ответ: г Пояснение: Когда сопротивление нагрузки линии передачи равно такая же, как у характеристического импеданса, линия считается согласованной.В таких случаях произойдет полная передача мощности с минимальными потерями.
Вопросы по электромагнитной теории для вступительных экзаменов — Sanfoundry, подготовленные персоналом10 В этом наборе вопросов и ответов по электромагнитной теории для вступительных экзаменов основное внимание уделяется «Вторичным параметрам линии передачи». 1. Длина волны линии с фазовой постоянной 6,28 единиц равна a) 2 b) 1 c) 0,5 d) 3.14 Просмотр ответа Ответ: b Пояснение: Длина волны и фазовая постоянная связаны соотношением λ = 2π / β, где β задается как 6.28. Подставив β, получим λ = 2π / 6,28 = 1 единицу. 2. Длина волны с частотой 6 ГГц в воздухе: a) 50 b) 5 c) 0,5 d) 0,05 Посмотреть ответ
Ответ: d Пояснение: длина волны определяется отношением скорости к частоте. волны. В воздушной среде скорость можно принять за скорость света. Подставляя v и f, мы получаем λ = v / f = 3 × 108/6 × 109 = 0,05 единиц. 3. Фазовая постоянная волны с длиной волны 2 единицы определяется выражением a) 2 b) 3,14 c) 6.28 d) 1 Просмотр ответа Ответ: b Пояснение: Фазовая постоянная определяется как β = 2π / λ. Подставляя λ = 2, получаем β = 2π / 2 = 3,14 единиц. 4. Частота волны, распространяющейся в линии передачи со скоростью 4 x 108 и длиной волны 3 единицы: a) 0,75 ГГц b) 0,133 ГГц c) 7,5 ГГц d) 1,33 ГГц Просмотр ответа Ответ: b Пояснение: соотношение частоты и длины волны задается формулой f = v / λ. Подставляя v и λ, получаем f = 4 x 108/3 = 0,133 ГГц. 5. Соотношение скорости и фазовой константы задается формулой a) V = ω / β b) V = ωβ c) V = β / ω d) Vωβ = 1 Посмотреть ответ Ответ: a Объяснение: Скорость волны — это отношение частоты в радианах в секунду до фазовой постоянной.Он задается формулой V = ω / β. 6. Найдите фазовую постоянную волны, распространяющейся со скоростью 1,2 x 108 и частотой 7,5 гига рад / сек a) 62,5 b) 26,5 c) 56,2 d) 52,6 Посмотреть ответ
Ответ: a Объяснение: Фазовая постоянная задается формулой β = ω / v из определения фазовой постоянной и скорости. Подставляя ω = 7,5 x 109 и v = 1,2 x 108, получаем фазовую постоянную β = 7,5 x 109 / 1,2 x 108 = 62,5 единиц. 7. Электрическая длина в линии передачи относится к a) произведению постоянной затухания и длины b) отношения постоянной затухания к длине c) произведения фазовой постоянной и длины d) отношения фазовой постоянной и длины Посмотреть ответ Ответ: a Объяснение : Электрическая длина в линии передачи относится к произведению постоянной затухания α и длины линии l.Он задается αl. 8. Единица измерения постоянной затухания: a) децибел b) бел c) непер d) без единицы измерения. Просмотр Ответ: c Пояснение: Константа затухания — это мера потерь мощности волны во время ее передачи. Он выражается в непер и 1 непер = 8,686 децибел / м. 9. Постоянная затухания вызывает искажение фазы, а постоянная фазы вызывает искажение частоты. Состояние Истина / Ложь. a) Верно b) Ложное мнение. Ответ: b Пояснение: Всегда есть какие-то искажения, даже в идеальной линии передачи.Это связано с вариацией второстепенных параметров. Константа затухания вызывает искажение частоты, а постоянная фазы вызывает искажение фазы. 10. Постоянная распространения волны с затуханием и фазовой постоянной, задаваемой соответственно 2 и 3, равна a) 2 — 3j b) 3 — 2j c) 2 + 3j d) 3 + 2j Просмотр ответа
Ответ: c Пояснение: постоянная распространения определяется выражением γ = α + jβ. Учитывая, что α = 2 и β = 3. Таким образом, мы получаем постоянную распространения как γ = 2 + 3j. 11.Скорость волны в воздушной среде: a) 1 x 108 b) 1,5 x 108 c) 3 x 108 d) 1 x 109 Посмотреть ответ Ответ: c Пояснение: Свет движется с максимальной скоростью в воздушной среде. Таким образом, предполагается, что скорость волны в воздушной среде равна скорости света. Он задается как c = 3 x 108. 12. Определите вторичный параметр из вариантов, приведенных ниже. a) Сопротивление b) Проводимость c) Фазовая постоянная d) Емкость Просмотр Ответ Ответ: c Пояснение: Первичные параметры непосредственно наблюдаются из характеристик схемы.Вторичные параметры выводятся или рассчитываются на основе первичных параметров. R, L, C, G — первичные параметры, тогда как α, β, γ, Zo — вторичные параметры.
Уравнения линии передачи Вопросы и ответы по электромагнитной теории — Sanfoundry by staff10 Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен «уравнениям линии передачи». 1. Какой из следующих параметров не существует в уравнении линии передачи? a) R b) Zo c) ZL d) Постоянная распространения Просмотр Ответ
Ответ: a Объяснение: Уравнение линии передачи состоит только из вторичных параметров, которые выводятся из первичных параметров.Постоянная распространения, полное сопротивление нагрузки и характеристическое сопротивление связаны в уравнении линии передачи. 2. Для бесконечной линии передачи характеристическое сопротивление равно 50 Ом. Найдите входное сопротивление. a) 25 b) 100 c) 2500 d) 50 Просмотр ответа Ответ: d Пояснение: Исходя из уравнения линии передачи, бесконечная линия будет иметь входной импеданс, такой же, как у характеристического импеданса. Таким образом, Zin = Zo для l-> ∞. Это показывает, что линия будет совпадать. Входное сопротивление для данного случая составляет 50 Ом.3. Наилучшая длина передачи для эффективной передачи мощности: a) L = λ / 4 b) L = λ / 8 c) L = λ / 2 d) L = ∞ Посмотреть ответ Ответ: b Пояснение: Максимальная передача мощности будет возникают, когда линия передачи совпадает. Это означает, что входное и характеристическое сопротивление одинаковы. Это условие возможно при l = λ / 8 и l = ∞. Поскольку l = ∞ невозможно, лучший вариант — l = λ / 8. 4. Когда длина линии передачи равна длине волны, какое условие выполняется? a) Zin = Zo b) Z = Zo c) ZL = Zo d) Zin = ZL Просмотреть ответ Ответ: d Объяснение: Когда линия передачи имеет длину, равную длине волны распространяющейся через нее волны, входное сопротивление будет таким же, как сопротивление нагрузки.Это тот случай, когда волна не усиливается. Линия передачи действует как буфер. 5. Входное сопротивление полуволновой линии передачи с сопротивлением нагрузки 12,5 Ом составляет а) 25 б) 50
в) 6,25 г) 12,5 Просмотр Ответ Ответ: г Пояснение: Для полуволновой линии передачи L = λ / 2, входное сопротивление и сопротивление нагрузки будут одинаковыми. Таким образом, для приведенных данных входное сопротивление будет 12,5 Ом. 6. Условие для четвертьволнового трансформатора: a) Zo2 = Zin ZL b) Zo = Zin ZL c) ZL2 = Zin Zo d) Zo = Zin Просмотр Ответ: a Объяснение: Четвертьволновый трансформатор представляет L = λ / 4 .В этом случае характеристический импеданс — это среднее геометрическое значений входного импеданса и импеданса нагрузки. Таким образом, Zo2 = Zin ZL — необходимое условие. 7. Найдите характеристический импеданс четверти волны с входным импедансом и импедансом нагрузки, равными 50 и 25 соответственно. a) 50 b) 25 c) 75 d) 35,35 Просмотр ответа Ответ: d Пояснение: для четвертьволновой волны характеристический импеданс является средним геометрическим входным импедансом и импедансом нагрузки. Таким образом, Zo2 = Zin ZL. Подставляя Zin = 50 и ZL = 25, получаем Zo2 = 50 x 25.Характеристическое сопротивление будет 35,35 Ом. 8. Найдите полное сопротивление нагрузки в трансформаторе четверть линии с характеристическим сопротивлением 75 Ом и входным сопротивлением 200 Ом. a) 28,125 b) 12,285 c) 52,185 d) 85,128 Просмотр ответа Ответ: a Пояснение: для четвертьволновой волны характеристический импеданс является средним геометрическим входным импедансом и импедансом нагрузки. Таким образом, Zo2 = Zin ZL. Подставляя Zo = 75 и Zin = 200, мы получаем ZL = Zo2 / Zin = 752/200 = 28,125 Ом.
9. Коэффициент отражения идеально согласованной линии передачи равен a) 1 b) -1 c) 0 d) ∞ Просмотр Ответ Ответ: c Объяснение: В идеально согласованной линии будет происходить передача максимальной мощности.Убытки будут минимальными. Это подразумевает единичный коэффициент передачи и нулевой коэффициент отражения. 10. Целью уравнения линии передачи является: а) найти первичные параметры б) найти вторичные параметры в) найти коэффициент отражения г) согласование импеданса Просмотр ответа: г Пояснение: Уравнение линии передачи полезно для определения длины линия, обеспечивающая максимальную передачу мощности. Таким образом, это полезно для согласования импеданса. 11. Четвертьволновый трансформатор может рассматриваться как aa) инвертор импеданса b) удвоитель импеданса c) утроенный импеданс d) учетверитель импеданса Посмотреть ответ Ответ: a Объяснение: четвертьволновой трансформатор можно рассматривать как инвертор импеданса, поскольку он может преобразовывать сопротивление в высокий импеданс и наоборот.12. Какая линия передачи называется трансформатором «один в один»? a) L = λ b) L = λ / 2 c) L = λ / 4 d) L = λ / 8 Посмотреть ответ Ответ: b Пояснение: Линия полуволнового трансформатора повторяет свой оконечный импеданс. Другими словами, когда l = λ / 2, Zin = ZL. Таким образом, это считается трансформатором «один в один».
Входные и характеристические импедансы Вопросы и ответы по электромагнитной теории — Sanfoundry by staff10 В этом наборе вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории основное внимание уделяется «Входным и характеристическим сопротивлениям».1. Характеристический импеданс четвертьволнового трансформатора с нагрузочным и входным сопротивлениями, заданными 30 и 75 соответственно, равен a) 47,43 b) 37,34 c) 73,23 d) 67,45 Просмотр Ответ Ответ: a Объяснение: В четвертьволновом трансформаторе характеристическое сопротивление будет быть средним геометрическим входным сопротивлением и сопротивлением нагрузки. Таким образом, Zo2 = ZIN ZL. Подставив ZIN = 75 и ZL = 30, мы получим характеристический импеданс как 47,43 единицы. 2. Входное сопротивление четвертьволновой линии 50 Ом и сопротивление нагрузки 20 Ом равно a) 50 b) 20 c) 1000 d) 125 Просмотр ответа Ответ: d Пояснение: характеристическое сопротивление будет средним геометрическим входным сопротивлением. и сопротивление нагрузки.Таким образом, Zo2 = Zin ZL. Подставив Zo = 50 и ZL = 20, мы получим входное сопротивление как 502/20 = 125 Ом. 3. Для согласованной линии входной импеданс будет равен а) импедансу нагрузки б) характеристическому сопротивлению в) выходному сопротивлению г) нулевому виду. Ответ Ответ: б Объяснение: согласованная линия означает, что входной и характеристический импеданс совпадают. В таких условиях
максимальная передача будет происходить с минимальными потерями. Отражение будет очень низким. 4. Коэффициент отражения находится в диапазоне a) 0
Ответ: a Пояснение: Групповая задержка определяется как td = β / ω.Учитывая, что β = 62,5 и ω = 4,5, мы получаем групповую задержку как td = 62,5 / 4,5 = 13,88 единиц. 8. Максимальный импеданс линии передачи 50 Ом и коэффициент стоячей волны 2,5: a) 20 b) 125 c) 200 d) 75 Просмотр Ответ: b Пояснение: Максимальный импеданс линии определяется выражением Zmax = SZo. . Подставляя S = 2,5 и Zo = 50, получаем Zmax = 2,5 x 50 = 125 Ом. 9. Минимальный импеданс линии передачи 75 Ом с коэффициентом стоячей волны 4 равен a) 75 b) 300 c) 18,75 d) 150 Просмотр Ответ Ответ: c Пояснение: Минимальное сопротивление линии определяется выражением Zmin = Zo. / С.Подставляя Zo = 75 и S = 4, получаем Zmin = 75/4 = 18,75 единиц. 10. Средняя мощность в электромагнитной волне определяется а) постоянной распространения б) вектором Пойнтинга в) фазовой постоянной г) постоянной затухания Просмотр Ответ Ответ: б Объяснение: Вектор Пойнтинга является взаимным произведением напряженности электрического и магнитного полей. . Он дает полную мощность электромагнитной волны. 11. Характеристическое сопротивление линии передачи обычно выбирается следующим образом: a) 50 b) 75 c) 50 или 75 d) 100 Посмотреть ответ
Ответ: c Пояснение: характеристическое сопротивление всегда составляет 50 Ом или 75 Ом для передачи. линия.Это связано с рабочим диапазоном ГГц и используемым сопротивлением нагрузке. 12. Определите материал, которого нет в установке линии передачи. a) волноводы b) объемный резонатор c) антенна d) осциллятор Просмотр Ответ Ответ: d Пояснение: Линия передачи состоит из антенн для передачи и приема мощности. Он состоит из волноводов и объемного резонатора для направленной передачи электромагнитных волн. Таким образом, осциллятор — лишний.
Вопросы и ответы о коэффициентах отражения и передачи — Sanfoundry, сотрудники10 Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен «коэффициентам отражения и передачи».1. Коэффициент отражения волны с коэффициентом передачи 0,35 составляет а) 1,35 б) 0,65 в) 0,35 г) 0,7 Просмотр Ответ Ответ: б Пояснение: Коэффициент отражения обратен коэффициенту передачи. Таким образом, T + R = 1. При замене T = 0,35 коэффициент отражения R будет 1 — 0,35 = 0,65 (без единицы измерения). 2. Амплитуда падающей волны 24 единицы. Найдите амплитуду отраженной волны, если коэффициент отражения равен 0,6. a) 14,4 b) 16,6 c) 13,3 d) 11.1 Просмотр ответа
Ответ: a Пояснение: Коэффициент отражения — это отношение амплитуды отраженного сигнала к амплитуде падения.Таким образом, R = Er / Ei. Подставляя Ei = 24 и R = 0,6, получаем Er = R Ei = 0,6 X 24 = 14,4 единиц. 3. Найдите коэффициент отражения волны, проходящей через две среды с внутренним импедансом 4 и 9 соответственно. a) 0,5 b) 1 c) 0,38 d) 0,1 Посмотреть ответ Ответ: c Пояснение: Коэффициент отражения в терминах собственных импедансов определяется выражением R = η2 — η1 / η2 + η1. Подставляя η1 = 4 и η2 = 9, получаем R = 9 — 4/9 + 4 = 5/13 = 0,38. 4. Коэффициент отражения волны, проходящей через две среды с диэлектрической проницаемостью 4 и 9 соответственно, равен a) 0 b) 0.5 c) 0,25 d) 0,2 Посмотреть ответ Ответ: d Пояснение: Коэффициент отражения с точки зрения диэлектрической проницаемости определяется как R = √ε2 — √ε1 / √ε2 + √ε1. Подставляя ε1 = 4 и ε2 = 9, получаем R = 3 — 2/3 + 2 = 1/5 = 0,2. 5. Рассчитайте коэффициент передачи, когда амплитуды падающего и прошедшего излучения равны 10 и 7 соответственно. a) 17 b) 3 c) 10/7 d) 0,7 Просмотр Ответ Ответ: d Пояснение: Коэффициент передачи определяется как отношение передаваемой амплитуды к падающей амплитуде. Таким образом, T = Et / Ei.Подставляя Ei = 10 и Et = 7, получаем T = 7/10 = 0,7. 6. Коэффициент передачи в волне, проходящей через две среды с внутренним импедансом 5,5 и 1,33, составляет: a) 0,389 b) 0,55
c) 0,133 d) 0,42 Просмотр ответа Ответ: a Объяснение: Коэффициент передачи является выражением внутреннего импеданса. задается формулой T = 2η2 / η1 + η2. Подставляя η1 = 5,5 и η2 = 1,33, получаем T = 2 x 1,33 / 1,33 + 5,5 = 2,66 / 6,83 = 0,389. 7. Коэффициент передачи в волне, проходящей через две среды с диэлектрической проницаемостью 4 и 1, равен a) 1/4 b) 3/2 c) 3/4 d) 2/3 Просмотр Ответ Ответ: d Пояснение: Коэффициент передачи в терминах диэлектрической проницаемости T = 2√ε2 / √ε1 + √ε2.Подставляя ε1 = 4 и ε2 = 1, получаем T = 2 (1) / 1 + 2 = 2/3. 8. Коэффициент отражения линии передачи с характеристическим сопротивлением нагрузки и сопротивлением нагрузки 50 и 30 Ом соответственно составляет a) 1/4 b) 1/8 c) 1/2 d) 3/4 Просмотр Ответ Ответ: a Пояснение: Отражение Коэффициент линии передачи определяется выражением R = ZL — Zo / ZL + Zo, где ZL и Zo — нагрузка и характеристические сопротивления соответственно. При подстановке ZL = 30 и Zo = 50 коэффициент отражения R = 50 — 30/50 + 30 = 20/80 = 1/4.9. В согласованной линии коэффициент передачи равен a) 0 b) 1 c) -1 d) Infinity View Ответ Ответ: b Пояснение: В согласованной линии максимальная мощность передается от передатчика к приемнику. Такой коэффициент отражения будет равен нулю, а коэффициент передачи равен единице.
10. Найдите мощность, отраженную в линии передачи, когда коэффициент отражения и входная мощность составляют 0,45 и 18 В соответственно. a) 3,645 b) 6,453 c) 4,563 d) 5,463 Просмотр Ответ Ответ: a Объяснение: Отношение амплитуды отраженного сигнала к амплитуде падения дает отражение.Точно так же отношение отраженной мощности к падающей дает квадрат коэффициента отражения. Таким образом, Prefl = R2Pinc. Подставив R = 0,45 и Pinc = 18, мы получим Prefl = 0,452 x 18 = 3,645 единиц. 11. Передаваемая мощность в линии передачи, когда коэффициент отражения и падающая мощность составляют 0,6 и 24 В соответственно, составляет a) 15,36 b) 51,63 c) 15,63 d) 51,36. коэффициент отражения и падающая мощность равны Ptr = (1-R2) Pinc, где R = 0.6 и Pinc = 24 по приведенным данным. Таким образом, Ptr = (1-0,62) x 24 = 15,36 единиц. 12. Коэффициент отражения линии передачи короткого замыкания равен -1. Состояние Истина / Ложь. a) Верно b) Ложный ответ Ответ: a Объяснение: Для линии короткого замыкания потери максимальны из-за протекания сильного тока. Это приводит к меньшей передаче и большему затуханию. Таким образом, коэффициент отражения отрицательный. R = 1 для линий короткого замыкания.
Вопросы по теории электромагнитного поля для собеседований в кампусе — Sanfoundry от персонала10 Этот набор вопросов и ответов по теории электромагнитного поля для собеседований в кампусе посвящен теме «Стоячие волны и КСВ».
1. Стоячие волны возникают из-за а) согласования импеданса б) несоответствия импеданса в) отражения г) обзора передачи Ответ Ответ: б Объяснение: Несоответствие импеданса приводит к возникновению стоячих волн вдоль линии передачи. Он показывает изменение амплитуд волн из-за рассогласования. 2. Коэффициент стоячей волны определяется как а) отношение максимумов напряжения к минимумам напряжения б) отношение максимумов тока к минимумам тока в) произведение максимумов напряжения и минимумов напряжения г) произведение максимумов тока и минимумов тока Просмотр ответа Ответ: a Пояснение: КСВ определяется как отношение амплитуды частичной стоячей волны в пучности (максимум) к амплитуде в узле (минимум) вдоль линии.Он задается как S = VMAX / VMIN. 3. Учитывая, что коэффициент отражения равен 0,6. Найдите КСВ. a) 2 b) 4 c) 6 d) 8 Посмотреть ответ Ответ: b Пояснение: Связь между коэффициентом отражения и КСВ определяется выражением S = 1 + R / 1 — R. Подставляя R = 0,6, мы получаем S = 1 + 0,6 / 1 — 0,6 = 1,6 / 0,4 = 4. 4. Максимальное и минимальное напряжение стоячей волны равны 6 и 2 соответственно. Коэффициент стоячей волны: a) 2 b) 3 c) 1/2 d) 4 Просмотр Ответ: b Пояснение: Отношение максимумов напряжения к минимумам напряжения дается коэффициентом стоячей волны КСВ.Таким образом, S = VMAX / VMIN. Подставляя данные данные, получаем S = 6/2 = 3.
5. Найдите коэффициент стоячей волны, когда сопротивление нагрузки 250 Ом подключено к линии 75 Ом. a) 0,3 b) 75 c) 250 d) 3.33 Просмотр ответа Ответ: d Пояснение: Коэффициент стоячей волны — это отношение импеданса нагрузки к характеристическому сопротивлению. Таким образом, S = ZL / Zo. Подставляя ZL = 250 и Zo = 75, получаем S = 250/75 = 3,33. 6. Найдите коэффициент отражения волны с КСВ 3,5. а) 0,55 б) 0,23 в) 0.48 d) 0,68 Просмотр ответа Ответ: a Пояснение: Коэффициент отражения в терминах КСВ равен R = S — 1 / S + 1. Подставляя S = 3,5, мы получаем 3,5 — 1 / 3,5 + 1 = 0,55. . 7. Диапазон коэффициента стоячей волны: a) 0
9. Максимальное сопротивление линии передачи 50 Ом с КСВ 3 равно a) 50/3 b) 3/50 c) 150 d) 450 Просмотр ответа Ответ : c Пояснение: Максимальный импеданс определяется произведением характеристического импеданса и КСВ. Таким образом, Zmax = S Zo. Подставляя S = 3 и Zo = 50, мы получаем ZMAX = 3 X 50 = 150 единиц.10. Минимальный импеданс линии передачи 75 Ом с КСВ 2,5 равен a) 100 b) 50 c) 25 d) 30 Просмотр Ответ: d Пояснение: Минимальный импеданс с точки зрения КСВ равен ZMIN = Zo / С. Подставляя данные данные для S = 2,5 и Zo = 75, получаем Zmin = 75 / 2,5 = 30. 11. Коэффициент стоячей волны короткозамкнутых и разомкнутых линий будет a) 0 b) 1 c) -1 d) ∞ Просмотр ответа Ответ: d Объяснение: Линия передачи будет отражать высокую мощность при коротком замыкании или замыкании. Это приведет к высокому коэффициенту отражения.Таким образом, для этих крайних случаев коэффициент стоячей волны будет бесконечным. 12. Текущий коэффициент отражения линии с коэффициентом отражения по напряжению 0,65 определяется выражением a) 0 b) 0,65 c) -0,65 d) 0,35 Просмотр Ответ Ответ: c Пояснение: Текущий коэффициент отражения в любой точке линии является отрицательное значение коэффициента отражения напряжения
в этой точке, т. е. -R. Учитывая, что коэффициент отражения по напряжению составляет 0,65, то коэффициент отражения по току составляет -0,65.
Питание, потери мощности и возвратные потери Вопросы и ответы по электромагнитной теории — Sanfoundry by staff10 Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен теме «Мощность, потери мощности и возвратные потери».1. Мощность электромагнитной волны с напряженностями электрического и магнитного поля, заданными числами 12 и 15 соответственно: a) 180 b) 90 c) 45 d) 120 Просмотр Ответ Ответ: b Пояснение: вектор Пойнтинга дает мощность электромагнитной волны. . Таким образом, P = EH / 2. Подставляя E = 12 и H = 15, получаем P = 12 x 15/2 = 90 единиц. 2. Мощность волны напряжением 140 В и характеристическим сопротивлением 50 Ом составляет а) 1,96 б) 19,6 в) 196 г) 19600 Посмотреть ответ Ответ: в Пояснение: Мощность волны определяется выражением P = V2. / 2Zo, где V — напряжение генератора, а Zo — характеристическое сопротивление.при подстановке приведенных данных получаем P = 1402 / (2 × 50) = 196 единиц. 3. Мощность, отраженная волной с падающей мощностью 16 единиц, равна (Учитывая, что коэффициент отражения равен 0,5) a) 2 b) 8 c) 6 d) 4 Просмотр Ответ
Ответ: d Пояснение: Доля отраженного падающей мощности определяется коэффициентом отражения. Таким образом, Pref = R2xPinc. Подставляя приведенные данные, получаем Pref = 0,52 x 16 = 4 единицы. 4. Мощность, передаваемая волной с падающей мощностью 16 единиц, равна (Учитывая, что коэффициент отражения равен 0.5) a) 12 b) 8 c) 16 d) 4 Просмотр Ответ: a Пояснение: доля переданной мощности в падающей мощности определяется коэффициентом отражения. Таким образом, Pref = (1-R2) Pinc. Подставляя приведенные данные, получаем Pref = (1-0,52) x 16 = 12 единиц. Другими словами, это оставшаяся мощность после отражения. 5. Падающее и отраженное напряжение равны 15 и 5 соответственно. Коэффициент передачи: a) 1/3 b) 2/3 c) 1 d) 3 View Ответ Ответ: b Пояснение: Отношение отраженного напряжения к падающему — это коэффициент отражения.Это даётся как R = 5/15 = 1/3. Чтобы получить коэффициент передачи, T = 1 — R = 1 — 1/3 = 2/3. 6. Текущий коэффициент отражения равен -0,75. Найдите коэффициент отражения по напряжению. a) -0,75 b) 0,25 c) -0,25 d) 0,75 Просмотр Ответ Ответ: d Пояснение: Коэффициент отражения напряжения является отрицательным по отношению к текущему коэффициенту отражения. Для коэффициента отражения тока -0,75 коэффициент отражения по напряжению будет 0,75. 7. Затухание дано на 20 единиц. Найдите потерю мощности в децибелах.a) 13.01 b) 26.02 c) 52.04
d) 104.08 Просмотр ответа Ответ: a Пояснение: Затухание относится к потере мощности. Таким образом, потеря мощности составляет 20 единиц. Потери мощности в дБ будут 10 log 20 = 13,01 децибел. 8. Коэффициент отражения 0,5. Найдите возвратный убыток. a) 12,12 b) -12,12 c) 6,02 d) -6,02 Посмотреть ответ Ответ: c Пояснение: Обратные потери задаются как RL = -20log R, где — коэффициент отражения. Он задан как 0,5. Таким образом, возвратные потери будут RL = -20 log 0.5 = 6,02 децибела. 9. Сопротивление излучения антенны, имеющей мощность 120 единиц и ток антенны 5A, составляет a) 4,8 b) 9,6 c) 3,6 d) 1,8 Просмотр Ответ Ответ: a Пояснение: Мощность антенны определяется выражением Prad = Ia2. Rrad, где Ia — ток антенны, Rrad — сопротивление излучения. Подставляя приведенные данные, получаем Rrad = Prad / Ia2 = 120/52 = 4.8 Ом. 10. Коэффициент передачи равен 0,65. Найдите обратные потери волны. a) 9,11 b) 1,99 c) 1,19 d) 9,91 Просмотр Ответ Ответ: a Пояснение: Коэффициент передачи обратен коэффициенту отражения, т.е.e, T + R = 1. Когда T = 0,65, мы получаем R = 0,35. Таким образом, возвратные потери RL = -20log R = -20log 0,35 = 9,11 децибел. 11. Обратные потери равны 12 децибелам. Рассчитайте коэффициент отражения. a) 0,35 b) 0,55
c) 0,25 d) 0,75 Просмотр ответа Ответ: c Пояснение: Обратные потери определяются как RL = -20log R. Коэффициент отражения можно рассчитать как R = 10 (-RL / 20), по свойству антилогарифма. Для заданных возвратных потерь RL = 12 получаем R = 10 (-12/20) = 0,25. 12. Найдите коэффициент передачи волны при обратных потерях 6 децибел.a) 0,498 b) 0,501 c) 0,35 d) 0,65 Посмотреть ответ Ответ: a Объяснение: Обратные потери определяются как RL = -20log R. Коэффициент отражения можно рассчитать как R = 10 (-RL / 20), с помощью анти логарифм свойство. Для заданных возвратных потерь RL = 6 получаем R = 10 (-6/20) = 0,501. Коэффициент передачи будет T = 1 — R = 1-0,501 = 0,498.
Проверка пригодности к электромагнитной теории Sanfoundry, разработанная персоналом10 Этот набор вопросов и ответов по электромагнитной теории для проверки пригодности фокусируется на «Внутреннем импедансе и константе распространения».1. Собственное сопротивление волны с электрическим и магнитным полями 10 и 8 соответственно равно a) 1,6 b) 1,11 c) 1,25 d) 0,8 Просмотр Ответ Ответ: b Пояснение: Собственное сопротивление волны определяется выражением η = √ (E / H). при замене E = 10 и H = 8 получаем η = 1,11 ед. 2. Собственный импеданс определяется как отношение магнитного поля к электрическому полю электромагнитной волны. Состояние истина / ложь а) Верно
б) Ложь Мнение Ответ: б Пояснение: Собственное полное сопротивление определяется как отношение напряженности электрического поля к напряженности магнитного поля.Обозначается он η. Это сложная величина. 3. Собственное полное сопротивление в свободном пространстве: a) 60π b) 12π c) 6π d) 120π Посмотреть ответ Ответ: d Пояснение: Собственное полное сопротивление свободного пространства — это отношение диэлектрической проницаемости к проницаемости. Для воздушной среды значение составляет 120π или 377 Ом. 4. Постоянная распространения — сложная величина. Укажите истину / ложь. a) Верно b) Ложный ответ. Ответ: a Объяснение: Константа распространения — это комплексная величина. Он задается формулой γ = α + jβ, где α — постоянная затухания, действительное значение, а β — фазовая постоянная, комплексное значение.5. Вычислите постоянную распространения волны с импедансом и адмиттансом, равными 32 и 12 соответственно. a) 19,6 b) 17,6 c) 15,6 d) 13,6 Просмотр ответа Ответ: a Пояснение: Постоянная распространения определяется как γ = √ (ZY), где Z — полное сопротивление, а Y — проводимость. Подставляя Z = 32 и Y = 12, получаем γ = 19,6 единиц. 6. Собственный угол равен 250, найдите угол потерь. a) 12,5 b) 50 c) 25 d) 75 Посмотреть ответ
Ответ: b Пояснение: угол потерь в два раза больше внутреннего угла.Он задается формулой δ = 2θn. При замене θn = 25 угол потерь δ = 2 (25) = 50 градусов. 7. Коэффициент стоячей волны для волны с максимальной и минимальной напряженностями электрического поля 12 и 4 равен a) 12 b) 4 c) 3 d) 48 Просмотр Ответ: c Пояснение: КСВ определяется как отношение максимального электрического поля. напряженности поля до минимальной напряженности поля. Он определяется как S = EMAX / EMIN. Таким образом, для приведенных данных S = 12/4 = 3. 8. Коэффициент стоячей волны для волны, проходящей через две среды с внутренним импедансом 3 и 2, равен a) 2⁄3 b) 3⁄2 c) 1⁄5 d) 5 Просмотр ответа Ответ: b Пояснение: Коэффициент стоячей волны задается отношением внутреннего импеданса среды 1 к внутреннему сопротивлению среды 2.Таким образом, S = η1 / η2. Подставляя η1 = 3 и η2 = 2, получаем S = 3/2. 9. Коэффициент отражения волны, проходящей через две среды с внутренним электрическим сопротивлением 3 и 5 соответственно, равен a) 2 b) 8 c) 5⁄3 d) 1/4 Просмотр Ответ: d Пояснение: Коэффициент отражения в терминах для собственного импеданса R = η2-η1 / η2 + η1. Подставляя приведенные данные, получаем R = 5 — 3/5 + 3 = 2/8 = ¼. 10. Коэффициент отражения волны, проходящей через две среды с внутренним магнитным сопротивлением 2 и 1 соответственно, равен a) 1⁄2 b) 1⁄3 c) 1⁄4
d) 1⁄5 Просмотр Ответ Ответ: b Пояснение : Коэффициент отражения в терминах собственного магнитного импеданса равен R = η1 — η2 / η1 + η2.Подставляя приведенные данные, получаем R = 2 — 1/2 + 1 = 1/3. 11. Коэффициент передачи волны, проходящей через две среды с внутренними электрическими сопротивлениями 3 и 2 соответственно, равен a) 2⁄2 b) 8⁄9 c) 4⁄5 d) 1⁄4 Просмотр Ответ: c Пояснение: Коэффициент передачи, выраженный в собственном импедансе, равен R = 2η2 / η2 + η1. Подставляя приведенные данные, получаем R = 2 x 2/2 + 3 = 4/5. 12. Коэффициент передачи волны, распространяющейся через две среды с внутренними электрическими сопротивлениями 3 и 4 соответственно, равен a) 2⁄3 b) 8⁄9 c) 2⁄5 d) 6⁄7 Посмотреть ответ Ответ: d Пояснение: коэффициент передачи, выраженный в собственном импедансе, равен R = 2η1 / η2 + η1.Подставляя приведенные данные, получаем R = 2 x 3⁄4 + 3 = 6/7.
Скин-эффект — Вопросы и ответы по электромагнитной теории — Sanfoundry by staff10 Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен «скин-эффекту». 1. Скин-эффект — это явление, наблюдаемое в a) изоляторах b) диэлектриках c) проводниках
d) Semiconductors View Ответ Ответ: c Объяснение: Кожа проводника позволяет определенному количеству электромагнитной энергии проходить через него.Это явление называется скин-эффектом. По этой причине электромагнитные волны не могут распространяться внутри проводника. 2. Глубина скин-фактора измеряется в a) метре b) миллиметре c) сантиметре d) микрометре. Вид Ответ Ответ: d Пояснение: Глубина, на которую электромагнитные волны проходят через проводник, очень мала. Измеряется в мкм. 3. Глубина скин-слоя рассчитывается по амплитуде волны. Укажите истину / ложь a) Верно b) Неверное представление Ответ: a Объяснение: Глубина скин-слоя — это мера глубины, до которой амплитуда электромагнитной волны уменьшится до 36.8% от первоначальной стоимости. Таким образом, его можно вычислить, если известна начальная амплитуда. 4. Константа затухания составляет 0,5 единицы. Глубина скин-слоя будет a) 0,5 b) 0,25 c) 2 d) 4 Просмотр Ответ: c Объяснение: Глубина скин-слоя является обратной величиной константы затухания. Таким образом, δ = 1 / α. Подставив α = 0,5, получим δ = 1 / 0,5 = 2 единицы. 5. Рассчитайте глубину скин-слоя проводника с проводимостью 200 единиц. Частота волны в воздухе 10 ГГц. а) 355,8 б) 3,558 в) 35,58
г) 0.3558 Просмотреть ответ Ответ: a Объяснение: Глубина скин-слоя рассчитывается по формуле δ = 1 / √ (πfμσ), где f — частота, μ — проницаемость, а σ — проводимость. Для приведенных данных, f = 10 x 109, μ = 4π x 10-7 в воздухе и σ = 200, получаем δ = 355,8 мкм. 6. Эффективное поверхностное сопротивление материала с проводимостью 120 и глубиной скин-слоя 2 мкм составляет a) 4,16 кОм b) 4,16 кОм c) 41,6 кОм d) 41,6 кОм Посмотреть ответ Ответ: a Пояснение: Эффективное сопротивление кожи равно определяется как Rs = 1 / δσ, где δ — толщина скин-слоя, а σ — проводимость.Для приведенных данных δ = 2 x 10-6 и σ = 120 получаем Rs = 1 / (120x2x10-6) = 4,16 кОм. 7. Какой параметр используется для определения глубины скин-слоя? a) Сопротивление постоянному току b) Сопротивление переменному току c) Диэлектрическая проницаемость d) Вид потенциала. Ответ Ответ: b Объяснение: Поскольку глубина скин-слоя варьируется для разных частот, ее можно использовать для расчета переменного сопротивления материала. 8. Соотношение между глубиной скин-слоя и частотой определяется следующим образом: a) глубина скин-слоя α fb) скин-фактора α 1 / fc) скин-слоя α √fd) скин-фактора α 1 / √f Просмотр Ответ Ответ: d Пояснение: Глубина скин-слоя задается формулой δ = 1 / √ (πfμσ).Таким образом, взаимосвязь между глубиной скин-слоя и частотой равна: скин-толщина α 1 / √f. 9. Идеальный диэлектрик действует как a) Идеальный передатчик b) Идеальный отражатель c) Плохой передатчик
d) Плохой отражатель Просмотр Ответ: a Объяснение: Идеальный диэлектрик действует как идеальный передатчик. Другими словами, волна, падающая на идеальный диэлектрик, будет полностью проходить через него. 10. Идеальный проводник действует как a) Идеальный передатчик b) Идеальный отражатель c) Плохой передатчик d) Плохой отражатель Просмотр Ответ Ответ: b Пояснение: Идеальный проводник действует как идеальный отражатель.Другими словами, волна, падающая на идеальный проводник, будет полностью отражена обратно в ту же среду. Не будет скин-эффекта. 11. Результирующее электрическое поле двух компонентов в направлениях x и y с амплитудами 6 и 8 соответственно равно a) 100 b) 36 c) 64 d) 10 Просмотр Ответ Ответ: d Пояснение: Дано результирующее электрическое поле двух компонентов. на E = √ (Ex2 + Ey2). Для приведенных данных электрическое поле будет E = √ (62 + 82) = 10 единиц. 12. Глубина скин-слоя волны, имеющей частоту 3 МГц и скорость 12 м / с: a) 2 b) 3 c) 4 d) 6 Просмотр ответа Ответ: c Объяснение: Скорость волны является произведением частота и глубина скин-слоя.Таким образом, v = f.δ. Чтобы получить δ, положим v = 12 и f = 3 МГц, получим δ = 12 / (3 × 106) = 4 мкм.
Типы линий передачи — Вопросы и ответы по электромагнитной теории — Sanfoundry
by staff10 Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен «Типам линий передачи». 1. Определите, что из перечисленного не является линией передачи? a) Телефонные линии b) Передача электроэнергии c) Подземные кабели d) Полостные резонаторы Просмотр ответа Ответ: d Пояснение: Типы линий передачи — телефонные линии, линии электропередачи, подземные кабели, коаксиальные кабели, волоконно-оптические кабели и т. д.Полостные резонаторы — это не линии передачи, это компоненты, которые способствуют максимальной передаче. 2. Открытая проводная линия передачи состоит из a) проводника b) диэлектрика c) как проводника, так и диэлектрика d) либо проводника, либо диэлектрика. Просмотр Ответ: c Пояснение: Открытый провод — это обычная форма линии передачи. Открытый провод состоит из жил. Считается, что проводники таких линий параллельны и разделены диэлектриком. 3. Телефонные линии и линии электропередачи — это открытые проводные линии передачи.Укажите истину / ложь. a) Верно b) Ложный ответ. Ответ: a Объяснение: открытые проводные линии длинные и используются для удаленной проводной связи. Такими линиями являются телефонные линии и линии электропередач. 4. Кабельная линия передачи состоит из a) проводников b) изоляторов c) изолированных проводов d) изолированных проводов с диэлектриком. Просмотр Ответ
Ответ: d Пояснение: Кабельные линии являются подземными линиями электропередачи. Линия состоит из сотен отдельных проводов с бумажной изоляцией, скрученных попарно и объединенных внутри защитного провода или пластмассовой оболочки, которая обычно представляет собой твердый диэлектрик.5. Жилы кабельной линии лежат перпендикулярно диэлектрику. Укажите истину / ложь. a) Верно b) Ложное мнение. Ответ: b Пояснение: Во всех линиях передачи проводники считаются параллельными с твердым диэлектриком. 6. Коаксиальный кабель состоит из a) проводников b) диэлектрика c) проводника с диэлектриком d) двух проводов с диэлектриком. Просмотр Ответ: d Пояснение: коаксиальный кабель состоит из полого проводника, а второй провод находится внутри и коаксиально трубка.Диэлектрик может быть твердым или газообразным. 7. Коаксиальный кабель используется для а) передачи телефонных кабелей б) передачи энергии в) передачи телевизионного сигнала г) передачи коротких волн Просмотр Ответ: в Пояснение: Практически коаксиальные кабели используются для передачи телевизионных сигналов от тарелка антенны к транспондеру. 8. Определите, какой тип волновода не относится. a) Прямоугольный b) Круглый c) Цилиндрический d) Полость резонатора Вид Ответ Ответ: d Пояснение: Прямоугольный волновод — это широко используемый волновод.Цилиндрический и круглый волноводы одинаковы. Полостной резонатор не является волноводом.
9. Диапазон частот, обрабатываемых волноводами: a) Гц b) кГц c) МГц d) ГГц Просмотр Ответ: d Пояснение: Волноводы работают в диапазоне ГГц. В частности, волноводы активны на частотах выше 6 ГГц. Диапазон составляет несколько десятков ГГц. За пределами этого диапазона передача осуществляется по оптоволоконным кабелям. 10. Диапазон частот, используемых коаксиальными кабелями: a) Гц b) кГц c) МГц d) ГГц Просмотр Ответ Ответ: c Пояснение: Коаксиальные кабели работают в диапазоне МГц.Основное приложение включает в себя передачу по кабельному телевидению. 11. Частота среза для работы волновода: a) 2 МГц b) 6 ГГц c) 4 МГц d) 6 МГц Просмотр Ответ: b Пояснение: Волноводы должны работать выше частоты среза 6 ГГц. Это приведет к эффективной передаче энергии. При частоте ниже этой приведет к затуханию. 12. Самым лучшим средством связи является а) Интернет б) Телефон в) Телевидение г) Радио Просмотр Ответ: а Объяснение: Хотя все средства связи используют радиочастоты, Интернет-связь является самой быстрой.Он включает электронную почту, голосовые сообщения, видео сообщения и т. Д. Телефон, телевидение и радио используют линии передачи для связи на частотах радио
, тогда как Интернет использует как проводные, так и беспроводные средства. Также в нем используется оптическое волокно, в котором в качестве среды используется свет, поскольку он быстрее радиосигналов.
Вопросы и ответы по электромагнитной теории линий без потерь и искажений — Sanfoundry by staff10 Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен теме «Линии без потерь и без искажений».1. Линия передачи считается без потерь, если: а) проводник идеален, а диэлектрик без потерь b) проводник идеален и диэлектрик с потерями c) проводник несовершенен, а диэлектрик с потерями d) проводник несовершенный, а диэлектрик без потерь Посмотреть ответ Ответ: a Объяснение: Линия передачи без потерь относится к линии без потерь или затухания. Это возможно только при идеальном проводнике и без потерь в диэлектрике. 2. Сопротивление линии передачи без потерь равно a) 0 b) 1 c) -1 d) Infinity View Ответ Ответ: a Объяснение: Линия передачи без потерь будет иметь минимальные потери мощности.Таким образом, в идеальных случаях сопротивление считается равным нулю. 3. Какие два параметра, приведенные ниже, равны нулю в строке без потерь? a) L, C b) C, G c) G, α d) R, L Просмотр Ответ Ответ: c Пояснение: Из-за минимальных потерь в линии передачи без потерь параметры проводимости
и константы затухания принимаются равными быть нулевым. На практике линия без потерь невозможна. 4. Характеристический импеданс линии, имеющей постоянные первичной обмотки L и C, равные 35 миллигенри и 70 мкФ соответственно, составляет a) 500 b) 22.36 c) 125 d) 50 Просмотр ответа Ответ: b Пояснение: Характеристический импеданс линии без потерь определяется выражением Zo = √ (L / C). Подставив L = 35 x 10-3 и C = 70 x 10-6, мы получим Zo = √ (500) = 22. 36 Ом. 5. Константа затухания измеряется в единицах: a) Ом b) Непер c) Децибел d) Радиан / сек Просмотр Ответ: b Пояснение: Затухание — это потеря мощности из-за передачи. Он измеряется в неперских единицах. 1 непер = 8,68 децибел / м. 6. Скорость линии передачи с частотой 35 рад / с и фазовой постоянной 68.5 — это а) 1,95 б) 2,36 в) 4,56 г) 3,48 Просмотр Ответ Ответ: а Объяснение: Скорость волны в линии передачи — это отношение частоты к фазовой постоянной. Таким образом, v = ω / β. Подставляя ω = 35 и β = 68,5, получаем v = 68,5 / 35 = 1,95 единиц. 7. Для линии передачи без искажений выполняется следующее условие: a) R / L = G / C b) RL = GC c) L / R = C / G d) RG / LC Просмотр Ответ
Ответ: a Пояснение: Для линии передачи без искажений первичные константы связаны соотношением R / L = G / C.8. Учитывая, что R = 20 Ом, L = 40 мГн, C = 40 мкФ, G = 0,02 мГн. Определите, без искажений ли линия. a) Линия с искажениями b) Линия без искажений c) Все вышеперечисленное d) Ни один из упомянутых View Answer: b Пояснение: Для линии без искажений должно выполняться условие R / L = G / C. Подставив R = 20, L = 40 мГн, C = 40 мкФ, G = 0,02, мы получим R / L = 500 и G / C = 500. Таким образом, линия не имеет искажений. 9. Для R = 20 Ом и G = 0,8 mho константа затухания будет a) 16 b) 4 c) 2 d) 32 Просмотр ответа Ответ: a Пояснение: Константа затухания определяется как α = √ (RG), где R и G — сопротивление и проводимость соответственно.Подставляя R = 20 и G = 0,8, получаем α = √ (20 x 0,8) = 4 единицы. 10. Скорость электромагнитной волны с частотой 6 МГц и толщиной скин-слоя 1,6 мкм. a) 3,75 b) 0,26 c) 9,6 d) 7,8 Просмотр Ответ Ответ: c Пояснение: Скорость волны является произведением частоты и глубины скин-слоя. Дано v = f. δ. Подставляя f = 6 x 106 и δ = 1,6 x 10-6, получаем v = 6 x 106 x 1,6 x 10-6 = 9,6 единиц. 11. Характеристическое сопротивление линии передачи с R = 45 Ом и G = 0.45 mho равно a) 100 b) 1 c) 0,1
d) 10 Посмотреть ответ Ответ: d Пояснение: характеристическое сопротивление в терминах R, G равно Zo = √ (R / G). Подставляя R = 45 и G = 0,45, получаем Zo = 10 единиц. 12. Линия без искажений — это линия, в которой постоянная затухания и фазовая постоянная не зависят от частоты. Укажите истину / ложь. a) Верно b) Ложное мнение. Ответ: b Объяснение: В линии без искажений постоянная затухания не зависит от частоты, а фазовая постоянная линейно зависит от частоты.
Вопросы для оценки электромагнитной теории — Sanfoundry, подготовленные персоналом10 В этом наборе вопросов и ответов для оценки электромагнитной теории основное внимание уделяется «диаграмме Смита». 1. Диаграмма Смита представляет собой полярную диаграмму, которая отображает а) R против Z b) R против Znorm c) T против Z d) T против Znorm Просмотр Ответ: b Пояснение: Диаграмма Смита представляет собой график в частотной области. Это полярная диаграмма коэффициента отражения R относительно нормированного импеданса Znorm. 2. Диаграмма Смита — это графический метод, используемый в сценарии линий передачи.Укажите истину / ложь. a) Верно b) Ложное мнение. Ответ
Ответ: a Пояснение: Диаграмма Смита используется для расчета коэффициента отражения и коэффициента стоячей волны для нормализованного импеданса нагрузки линии передачи. 3. Диаграмма Смита состоит из а) кружков постоянной R и переменной X б) кружков переменной R и постоянной X c) кружков постоянной R и постоянной X d) кружков переменной R и переменной X Просмотр ответа Ответ: c Пояснение: Диаграмма Смита состоит из кругов постоянного сопротивления и кругов постоянного реактивного сопротивления.Импедансы показаны с помощью этих кругов. Также сопоставление заглушек можно выполнить с помощью диаграммы Смита. 4. Через какую точку проходят круги на диаграмме Смита? a) (0,1) b) (0, -1) c) (-1,0) d) (1,0) Просмотр ответа Ответ: d Пояснение: все круги постоянного сопротивления и реактивного сопротивления на диаграмме Смита проходят через точка (1,0). Это середина диаграммы Смита. В этот момент сопротивление равно единице, а реактивное сопротивление равно нулю. 5. Движение по часовой стрелке на диаграмме Смита подразумевает движение а) к генератору б) к нагрузке в) к шлейфу г) в сторону волновода. к генератору.Это используется для расчета нормализованного импеданса нагрузки. 6. Центр точки с нормированным сопротивлением 1,2 Ом и реактивным сопротивлением 1,5 Ом равен a) (0,54,0) b) (0,45,0) c) (0,36,0) d) (0,78,0) Посмотреть ответ
Ответ: a Объяснение: Центр точки на диаграмме Смита равен C = (r / 1 + r, 0). Подставив r = 1,2, мы получим центр как (1,2 / 1 + 1,2,0) = (0,54,0). 7. Нормализованное сопротивление нагрузки линии передачи 50 Ом с нагрузкой 30 Ом равно a) 30 b) 150 c) 5/3 d) 3/5 Просмотр Ответ: d Пояснение: Нормализованное сопротивление рассчитывается путем деления на импеданс с характеристическим сопротивлением.Учитывая, что сопротивление нагрузки составляет 30 Ом, нормализованное сопротивление нагрузки линии передачи 50 Ом составляет 30/50 = 3/5 Ом. 8. Радиус точки с нормированным сопротивлением 1 Ом равен a) 1 b) 0,2 c) 0,5 d) 0,25 Просмотр Ответ Ответ: c Пояснение: Радиус точки с радиусом r определяется как R = 1 / г + 1. Подставив r = 1, получим R = 1/1 + 1 = ½ = 0,5. 9. Наилучшим выбором шлейфа для линии передачи будет a) Последовательный открытый b) Последовательный короткий c) Открытый шунт d) Короткий шунт Просмотр Ответ Ответ: d Объяснение: Обычно последовательные шлейфы не являются предпочтительными, поскольку изменение параметров шлейфа требует изменения вся настройка заглушки.Шунтирующие заглушки позволяют легко модифицировать. Шлейфы с разомкнутой цепью не являются предпочтительными, так как они будут излучать энергию, как антенна, что нежелательно. Следовательно, используются закороченные заглушки. 10. Центр и радиус линии с нормализованным сопротивлением нагрузки 1 + 0,5j равны a) (1,2) и 2 b) (2,1) и 2 c) (1,2) и 1 d) (2 , 1) и 1 Посмотреть ответ
Ответ: a Объяснение: Центр и радиус линии равны (1, 1 / x) и 1 / x, где x — реактивное сопротивление. Здесь x = 0,5, по приведенным данным. Таким образом, C = (1,2) и R = 2.
Линии короткого замыкания и разомкнутой цепи Вопросы и ответы по электромагнитной теории — Sanfoundry by staff10 Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен теме «Линии короткого и разомкнутого замыкания». 1. Импеданс разомкнутой цепи линии передачи определяется следующим образом: a) ZOC = j Zo tan βl b) ZOC = — j Zo tan βl c) ZOC = j Zo cot βl d) ZOC = -j Zo cot βl Посмотреть ответ Ответ : d Пояснение: Разрыв цепи в линии передачи относится к разомкнутой цепи со стороны нагрузки.В этом случае сопротивление нагрузки будет бесконечным. Таким образом, уравнение линии передачи будет ZOC = -j Zo cot βl. 2. Полное сопротивление короткого замыкания линии передачи определяется следующим образом: a) ZSC = j Zo tan βl b) ZSC = -j Zo tan βl c) ZSC = j Zo cot βl d) ZSC = -j Zo cot βl Посмотреть ответ Ответ : a Объяснение: Короткое замыкание в линии передачи относится к короткому замыканию на стороне нагрузки. В этом случае сопротивление нагрузки будет равно нулю. Таким образом, уравнение линии передачи будет ZSC = j Zo tan βl. 3. В закороченной линии коэффициент отражения будет a) 0 b) 1 c) -1 d) ∞ Просмотр Ответ
Ответ: c Пояснение: Закороченная линия потребляет больше энергии, чем любая другая линия.Таким образом, коэффициент отражения считается отрицательным. 4. Линия разомкнутой цепи будет иметь коэффициент отражения a) 0 b) 1 c) -1 d) ∞ Просмотр Ответ Ответ: b Пояснение: Линия разомкнутой цепи имеет бесконечное выходное сопротивление. Любая волна, падающая на выход, будет полностью отражена. Таким образом, коэффициент отражения равен единице. 5. Коэффициент стоячей волны в линиях передачи с короткими и разомкнутыми цепями будет a) 0 b) -1 c) 1 d) ∞ Просмотр Ответ Ответ: d Пояснение: Коэффициент отражения составляет 1 и -1 в разомкнутых и замкнутых линиях соответственно.Это значение коэффициента отражения даст бесконечный коэффициент стоячей волны. 6. Характеристический импеданс линии, имеющей полное сопротивление открытого и короткого замыкания 20 и 5 соответственно: a) 20 b) 100 c) 25 d) 10 Просмотр Ответ: d Пояснение: Характеристическое сопротивление — это среднее геометрическое значение короткого и открытого замыкания. сопротивление цепи. Он задается формулой Zo2 = Zsc Zoc. Подставляя Zoc = 20 и Zsc = 5, мы получаем Zo2 = 20 X 5 = 100. Таким образом, Zo = 10 Ом. 7. Полное сопротивление короткого замыкания равно 18 Ом, а характеристическое сопротивление — 50 Ом.Найдите полное сопротивление холостого хода. a) 138,8 b) 188,3 c) 388,1 d) 838,1 Посмотреть ответ
Ответ: a Пояснение: Соотношение между характеристическим сопротивлением, открытым и коротким сопротивлением определяется выражением Zo2 = Zsc Zoc. Для заданных значений Zo = 50 и Zsc = 18 получаем Zoc = 502/18 = 138,8 единиц. 8. Для применения теоремы о максимальной передаче мощности к линии передачи коэффициент отражения должен быть a) 1 b) -1 c) 0 d) ∞ Просмотр Ответ Ответ: c Объяснение: Максимальная передача мощности между нагрузкой и источником составляет возможно, только когда оба совпадают.Это не приведет к отражениям. Таким образом, коэффициент отражения будет равен нулю. 9. Найдите коэффициент передачи линии 75 Ом с сопротивлением нагрузки 40 Ом. a) 0,69 b) 0,96 c) 0,31 d) 0,13 Посмотреть ответ Ответ: a Пояснение: Коэффициент передачи с точки зрения импеданса нагрузки определяется выражением T = ZL / Z0. Подставляя ZL = 40 и Zo = 75, получаем T = 40/75 = 0,69. 10. Стоячие волны для напряжения холостого хода и тока короткого замыкания одинаковы. Укажите истину / ложь. a) Верно b) Ложный ответ Ответ: a Объяснение: Напряжение холостого хода и ток короткого замыкания будут одинаковыми для линии передачи.Разность фаз составляет λ / 8. 11. Стоячие волны для тока холостого хода и напряжения короткого замыкания одинаковы. Укажите истину / ложь. a) истина b) ложь Просмотр ответа Ответ: a Объяснение: Ток холостого хода и напряжение короткого замыкания будут одинаковыми для линии передачи. Разность фаз составляет λ / 8.
12. Коэффициент стоячей волны для максимальной передачи мощности в линии передачи составляет a) 1: 2 b) 2: 1 c) -1: 1 d) 1: 1 Просмотр ответа Ответ: d Пояснение: нагрузка и источник должен быть согласован для максимальной передачи мощности.На это указывает соотношение 1: 1.
Основы первичных цепей распределения (ответвления подстанции, фидеры …)
Типовая цепь распределения
Цепи распределения бывают разных конфигураций и длин цепей. Большинство из них имеют много общих характеристик. На рисунке 1 показана типовая распределительная цепь , а в таблице 1 показаны типичные параметры распределительной цепи.
Высоковольтная подстанция на острове Суон (фото предоставлено Шоном Трейси через Flickr)Фидер — это одна из цепей, выходящих за пределы подстанции. Главный фидер — это трехфазная магистраль цепи, которую часто называют сетью или магистралью. Магистраль обычно представляет собой небольшой провод, такой как алюминиевый провод на 500 или 750 километров в миллиметрах.
Коммунальные предприятия часто проектируют главный фидер на 400 A и часто допускают аварийный номинал 600 A. Ответвления от сети представляют собой один или несколько боковых ответвлений, которые также называются ответвлениями, боковыми ответвителями, ответвлениями или ответвлениями. Эти отводы могут быть однофазными, двухфазными или трехфазными.
Отводы обычно имеют предохранители, чтобы отделить их от магистрали в случае их неисправности.
Рисунок 1 — Типовая распределительная подстанция с одним из нескольких показанных фидеровНаиболее распространенными первичными распределительными устройствами являются системы с несколькими заземлениями «наш провод» : трехфазные проводники плюс многозаземленная нейтраль. Однофазные нагрузки обслуживаются трансформаторами, включенными между одной фазой и нейтралью.
Нейтраль действует как обратный провод и как защитное заземление оборудования (она заземляется периодически и на всем оборудовании).
Таблица 1 — Типовые параметры распределительной цепи
| Наиболее распространенное значение | Другие стандартные значения | ||||
| Характеристики подстанции | |||||
| Напряжение | 12,47 13,8, 24,94, 34,5 кВ | ||||
| Количество подстанционных трансформаторов | 2 | 1-6 | |||
| Размер трансформатора подстанции | 21 МВА | 5-60 МВА | |||
| шина | Количество фидеров 41-8 | ||||
| Характеристики фидера | |||||
| Пиковый ток | 400 A | 199 — 630A | |||
| Пиковая нагрузка | 7 МВА | Мощность | фактор | 0.98 с запаздыванием | 0,8 с запаздыванием / 0,95 вперед |
| Количество клиентов | 400 | 50-5000 | |||
| Длина питающей сети | 4 мили | 2-15 миль | |||
| Длина | |||||
| 8 миль | 4-25 миль | ||||
| Зона покрытия | 25 миль 2 | 0,5 — 500 миль 2 | |||
| Размер сетевого провода | 500 килобайт | ||||
| Размер провода бокового отвода | 1/0 | # 4-2 / 0 | |||
| Пиковый ток бокового отвода | 25 A | 5-50 A | |||
| Длина бокового отвода | 0.5 миль | 0,2 — 5 миль | |||
| Размер распределительного трансформатора (1 фаза) | 25 кВА | 10–150 кВА | |||
Однофазная линия имеет один фазный провод и нейтраль, а также два- фазовая линия имеет две фазы и нейтраль. Некоторые первичные распределительные устройства представляют собой трехпроводные системы (без нейтрали). На них однофазные нагрузки подключаются между фазами, а однофазные линии имеют две из трех фаз.
Существует несколько конфигураций распределительных систем.Большинство распределительных цепей являются радиальными (как первичными, так и вторичными).
Радиальные схемы имеют много преимуществ по сравнению с сетевыми схемами, в том числе:
- Более простая защита от тока короткого замыкания
- Более низкие токи короткого замыкания по большей части схемы
- Более легкое управление напряжением
- Более легкое прогнозирование и управление потоками мощности
- Более низкая стоимость
Распределительные первичные системы бывают разных форм и размеров (рис. 2). Компоновка зависит от планировки улиц, формы территории, на которой проходит трасса, препятствий (например, озер) и мест, где находятся большие грузы.
Рисунок 2 — Общие распределительные первичные устройстваОбычная пригородная планировка: основной подъезд вдоль улицы с боковыми ответвлениями, выходящими на переулки или в застройки .
Радиальные распределительные фидеры также могут иметь обширные разветвления — все, что требуется для доступа к нагрузкам. Экспресс-фидер обслуживает концентрацию нагрузки на некотором удалении от подстанции. Трехфазная магистраль проходит определенное расстояние, прежде чем отводить нагрузки потребителям.
При большом количестве цепей, идущих от одной подстанции , некоторые цепи могут иметь экспресс-фидеры .Некоторые фидеры покрывают территории, близкие к подстанции, а экспресс-фидеры обслуживают зоны дальше от подстанции.
Для повышения надежности радиальные цепи часто снабжены нормально разомкнутыми связующими точками с другими цепями, как показано на Рисунке 3. Цепи по-прежнему работают в радиальном направлении, но если в одной из цепей возникает неисправность, переключатели связи позволяют некоторую часть неисправную цепь необходимо быстро восстановить.
Обычно этими переключателями управляют вручную, но некоторые утилиты используют автоматические переключатели или устройства повторного включения для автоматического выполнения этих операций.
Рисунок 3 — Две радиальные цепи с нормально разомкнутыми связями друг с другомСхема первичного контура — еще более надежная услуга, которая иногда предлагается для критических нагрузок, таких как больницы. На рисунке 4 показан пример первичного контура. Ключевой особенностью является то, что цепь «проложена через» каждый критически важный трансформатор потребителя.
Если какая-либо часть первичной цепи выходит из строя, все критические потребители все еще могут получать питание путем перенастройки трансформаторных переключателей .
Системы первичного контура иногда используются в распределительных системах для областей, требующих высокой надежности (что означает ограниченные длительные прерывания).В конструкции с разомкнутым контуром, где в какой-то момент контур остается нормально разомкнутым, системы с первичным контуром почти не имеют преимуществ при кратковременных прерываниях или провалах напряжения. Они редко работают в замкнутом контуре.
Рисунок 4 — Схема распределения первичного контураШироко известная установка сложной замкнутой системы была установлена в Орландо, Флорида, компанией Florida Power Corporation. Пример этого типа первичной системы с замкнутым контуром показан на рисунке 4.
Неисправности любого из кабелей в контуре устраняются менее чем за шесть циклов , что сокращает продолжительность падения напряжения во время повреждения ( достаточно, чтобы помочь многим компьютерам).Усовершенствованная релейная защита, аналогичная защите линии передачи, необходима для координации защиты и работы распределительного устройства в замкнутой системе.
В схеме ретрансляции используется переключение с допустимым выходом за пределы допустимого диапазона (реле на каждом конце кабеля должны согласовывать наличие неисправности между ними, и связь осуществляется по оптоволоконным линиям).
В схеме резервного копирования используются направленные реле, которые срабатывают при неисправности в определенном направлении, если от удаленного конца не будет получен сигнал блокировки (опять же по оптоволоконным линиям).
Рисунок 5 — Пример системы распределения с обратной связьюУ критических клиентов есть еще два варианта более надежного обслуживания, когда доступны два основных источника питания. Первичная селективная и вторичная селективные схемы обычно питаются от одной цепи (см. Рисунок 5 выше).
Итак, схемы по-прежнему радиальные. В случае неисправности первичного контура услуга переключается на резервный контур. В первичной селективной схеме переключение происходит на первичной, а во вторичной селективной схеме переключение происходит на вторичной.Переключение может выполняться вручную или автоматически, и есть даже статические переключатели, которые могут переключаться менее чем за половину цикла, чтобы уменьшить мгновенные прерывания и провалы напряжения.
Сегодня предпочтение отдается первичной селективной схеме в основном из-за затрат, связанных с дополнительным трансформатором во вторичной селективной схеме .
Нормально замкнутый переключатель на переключателе первичной стороны размыкается после обнаружения потери напряжения. Обычно он имеет задержку времени порядка секунд — достаточную для прохождения нормального цикла повторного включения распределительной цепи.Отключение переключателя блокируется, если в переключателе есть перегрузка по току (переключатель не имеет возможности отключения при отказе). Передача также отключается, если альтернативное питание не имеет надлежащего напряжения.
Коммутатор может вернуться в нормальное состояние через разомкнутый или замкнутый переход. При закрытом переходе обе распределительные цепи временно включаются параллельно.
Ссылка // Электрораспределительное оборудование и системы / Т.А. Короткие (покупка на Amazon)
Что такое линии передачи? Определение, типы, параметры, свойства и применение линий передачи
Определение : Линии передачи — это проводники, которые служат путем для передачи (посылки) через них электрических волн (энергии).Они в основном образуют соединение между передатчиком и приемником, чтобы разрешал передачу сигнала .
Линии передачи в микроволновой технике известны как сетей с распределенными параметрами . Поскольку их напряжение и ток изменяются по всей длине. Он позволяет передавать электрические сигналы с помощью пары проводящих проводов, отделенных друг от друга диэлектрической средой, обычно являющейся воздухом.
Содержание: линии передачи
- Введение
- Типы
- Параметры
- Недвижимость
- Приложения
Введение
На рисунке ниже представлена эквивалентная принципиальная схема линии передачи:
Здесь два проводящих провода имеют определенную длину, а параметры линии передачи распределены по всей ее длине.Это параметры R, L, C и G , которые мы подробно обсудим в следующем разделе. Два проводящих провода из-за разделения обладают некоторой емкостью. Но эта диэлектрическая среда не обеспечивает полной изоляции, поэтому через нее протекает некоторый ток утечки.
Телефонные линии и линии электроснабжения являются некоторыми примерами линий электропередачи.
Типы линий передачи
Линии электропередачи в основном делятся на три категории:
Открытая линия передачи : это проводники, имеющие 2 линии (провода), разделенные диэлектрической средой, один конец которой подключен к источнику, а другой — к месту назначения.Это недорогие и самые простые линии передачи. Но стоимость их установки несколько выше, а обслуживание иногда затрудняется из-за изменения атмосферных условий.
На рисунке ниже представлена линия передачи с разомкнутым проводом:
Коаксиальные кабельные линии : Эти линии образуются, когда проводящий провод коаксиально вставляется внутрь другого полого проводника. Они называются коаксиальными, поскольку 2 проводника имеют одну и ту же ось.Они широко используются в приложениях, где требуются высокие уровни напряжения.
На рисунке ниже представлена линия передачи по коаксиальному кабелю:
Волноводы : Линия передачи этой категории используется для передачи сигналов на микроволновых частотах. В основном это полые проводящие трубки, поскольку они чем-то напоминают линию коаксиального кабеля, но не имеют центрального проводника, как в коаксиальных кабелях.
На рисунке ниже представлена линия передачи в виде волновода:
Параметры ЛЭП
При передаче сигнала по проводнику необходимо иметь представление о связанных с ним параметрах.Итак, в основном, существует 4 параметра, связанных с линией передачи.
- Сопротивление : Этот параметр любой линии передачи зависит от площади поперечного сечения проводящего материала. Как мы уже обсуждали, это сети с распределенными параметрами, что означает, что их параметры распределены равномерно по всей длине. Он обозначается буквой R, и его единица измерения — омы на единицу длины проводника.
Выдан:
: ρ обозначает проводимость проводящего материала
l обозначает длину ЛЭП, а
a обозначает площадь поперечного сечения линии
Здесь следует отметить, что сопротивление показывает изменение температуры и частоты подаваемого на него сигнала.
- Емкость : Как мы уже обсуждали, линия передачи состоит из 2 параллельных проводящих проводов, разделенных диэлектрическим материалом. Таким образом, он ведет себя как конденсатор с параллельными пластинами. Таким образом, он имеет некоторую емкость, которая также равномерно распределена по его длине. Он измеряется в фарадах на единицу длины проводника.
- Индуктивность : Когда ток течет по проводнику, он создает магнитное поле, перпендикулярное направлению электрического поля.При изменении магнитного поля в линии генерируется электромагнитный поток. Таким образом, теперь эта ЭДС течет в противоположном направлении с током, протекающим через устройство, который известен как индуктивность. Его величина зависит от тока, протекающего по проводнику. Индуктивность обозначается буквой L, а ее единицей является Генри на единицу длины проводника.
- Проводимость : два параллельных проводника разделены диэлектрической средой, но это не идеальный изолятор.Из-за чего через диэлектрик также протекает некоторый ток. Этот ток называется током утечки , и он отвечает за проводимость утечки через линию передачи. Он в основном присутствует между проводящими проводами и обозначается буквой G. Его единица измерения — mho на единицу длины проводника. Итак, четыре параметра линии передачи представлены как R, L, C и G.
Свойства ЛЭП
Линия передачи, которая позволяет распространять электрические волны, должна быть однородной, а также симметричной по своей природе, чтобы обеспечить удобную передачу.Итак, в принципе, существует 2 электрических свойства любой симметричной сети.
- Характеристическое сопротивление (Z 0 ) :
Предположим, что электрическая волна проходит от одного конца к другому по однородной линии передачи, а также по линии передачи без потерь. Тогда отношение напряжения, соответствующего линии передачи, и эквивалентного тока, протекающего по ней, называется характеристическим сопротивлением. Здесь следует отметить, что отражения прошедшей волны не произойдет.Выдается:
В параметрах характеристический импеданс представлен как:
Когда мы рассматриваем линию передачи без потерь, то она определяется как:
Считается, что симметричная сеть точно оконцована, если характеристическое сопротивление на обоих ее концах уравновешено.
- Константа распространения () :
Постоянная распространения линии передачи определяется как отношение тока, достигаемого на выходе, к току, приложенному на входе системы.Дается как
: ϒ обозначает комплексную величину, представленную α + jβ
Здесь α — постоянная затухания, а β — фазовая постоянная.
Применение линий электропередачи
Для передачи сигнала с высокочастотным диапазоном на короткие и большие расстояния используются линии передачи. В то же время это снижает потери мощности во время передачи.

