2.10. Параллельное соединение приемников в цепи синусоидального тока
Рассмотрим цепь с параллельным соединением приемников, представленную на рис. 2.16, а. Характерной особенностью такой цепи является то, что все приемники в цепи в целом находятся под одним и тем же напряжением U. Поэтому построение векторной диаграммы (рис. 2.16,6) этой цепи удобно начинать с вектора напряжения, после чего под соответствующими углами откладывают токи I1, I2, I3, а ток I в неразветвленной части цепи, как результирующий ток цепи, будет представлять собой геометрическую сумму векторов в параллельных ветвях. Такая диаграмма называется векторной диаграммой токов.
На векторной диаграмме рис. 2.16,б за исходный вектор взят вектор напряжения цепи (как общий для всех ветвей), который направлен по положительной оси комплексной плоскости. Относительно вектора напряжения отложены векторыкоторые отстают по фазе от напряжения соответственно на углыа также векторопережающий по фазе вектор напряжения на уголВектор токав неразветвленном участке цепи равен геометрической сумме векторов токов в параллельных ветвяхи отстает по фазе от вектора напряжения на угол
Согласно первому закону Кирхгофа, ток в неразветвленной части цепи в комплексной форме
(2.
64)
Здесь
Выразив токи через напряжение и полные сопротивления для уравнения (2.64) получим
(2.65)
где- комплекс эквивалентного полного сопротивления цепи;— комплексы полных сопротивлений соответствующих параллельных ветвей. Из (2.65) имеем
(2.66)
При анализе цепей с параллельным соединением приемников более удобно вместо сопротивлений ветвей брать их проводимости. Величина, обратная комплексу полного сопротивленияназывается комплексом полной проводимости
Выразив в (2.64) токи через напряжения и полные проводимости, получим
(2.68)
Следовательно, комплекс эквивалентной полной проводимости Y при параллельном соединении приемников равен сумме комплексов полных проводимостей отдельных параллельных ветвей.
Из (2.68) следует,
что эквивалентная полная проводимость
цепи при параллельном соединении ветвей
всегда больше наибольшей проводимости
любой из ветвей соединения, а так как
то эквивалентное полное сопротивление
параллельного соединения всегда меньше
наименьшего сопротивления соединения.
Если имеется параллельная rL-цепь, то комплекс полного сопротивления а комплекс полной проводимости
(2.69)
или
где — активная проводимость; —реактивная индуктивная проводимость;— модуль полной проводимости.
Если имеем rC-цепь, то комплекс полного сопротивления а комплекс полной проводимости
(2.70)
где — реактивная емкостная проводимость;— модуль полной проводимости.
Таким образом, мнимая часть комплекса полной проводимости положительна для rC-цепи и отрицательна для rL-цепи.
Если имеется rLC-цепь, то комплекс полного сопротивления и комплекс полной проводимости
(2.71)
или
где— модуль полной проводимости;- реактивная проводимость.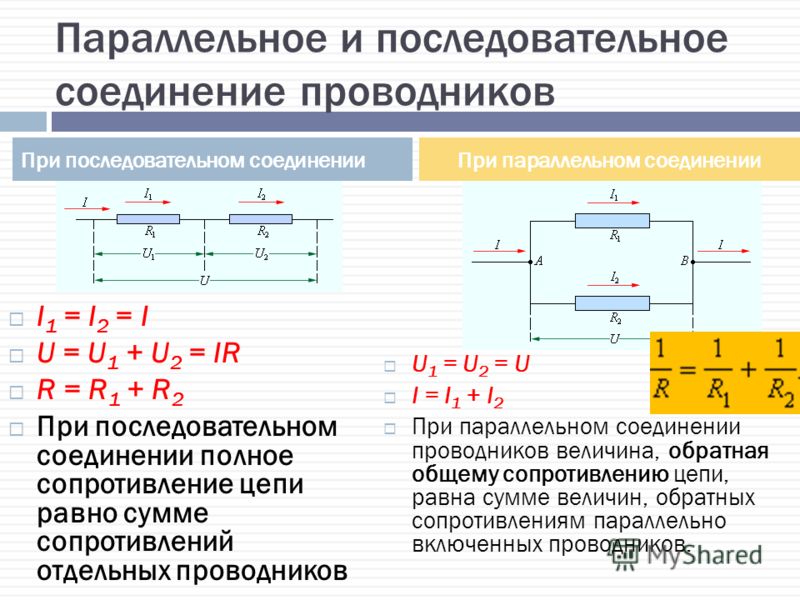
В (2.71) перед
мнимой частью ставят знак плюс, еслии знак минус, если
Ток в любой ветви параллельного соединения можно согласно закону Ома определить по формуле
(2.72)
где — комплекс активной составляющей тока; — комплекс реактивной составляющей тока.
Комплекс реактивной составляющей тока для индуктивной цепи а для емкостнойЕсли же в rLC-цепи
то перед комплексом реактивной составляющей тока ставят знак плюс, а если- знак минус.
При анализе режимов разветвленной цепи пользуются активными и реактивными составляющими тока и напряжения. В качестве примера рассмотрим цепь рис. 2.16, а, для которой комплекс эквивалентной полной проводимости
(2.73)
Если то перед мнимой частью комплексаставят знак минус, если жето знак плюс.
Из (2.73) следует, что эквивалентная активная проводимость параллельного соединения ветвей цепи равна арифметической сумме активных проводимостей отдельных параллельно включенных ветвей:
(2.
74)
Эквивалентная реактивная проводимость параллельного соединения ветвей цепи равна алгебраической сумме реактивных проводимостей отдельных параллельно включенных ветвей:
(2.75)
На рис. 2.16,6 треугольник Оbс, каждая из сторон которого представляет соответствующее значение тока, называется треугольником токов. Из треугольника токов имеем
Активная составляющая тока определяет активную мощность цепи:
Реактивная составляющая тока определяет реактивную мощность цепи:
Разделив все стороны треугольника токов (рис. 2.16,6) на напряжение U, получим подобный треугольник проводимостей (рис. 2.16, в), из которого имеем следующие соотношения:
Пример 2.5.
В цепи с последовательным соединением
катушки с параметрами R, L с конденсатором
плавно изменяется емкость
С конденсатора.
При максимальном токе
в цепи сняты показания приборов:
А —10
А, V—100
В, Vc
—250 В. Частота тока в цепи 50
Гц. Определить параметры цепи С, R,
L
и показания
вольтметра Vк,
подключенного
к выводам катушки.
Рисунок к примеру 2.5.
Решение. Так как ток максимальный, то в цепи имеет место резонанс напряжений, при котором UL= Uc = 250 В, UR = U = 100 В. Напряжение на катушке
Емкостное сопротивление XC = UC/I = 250/10 = 25 Ом.
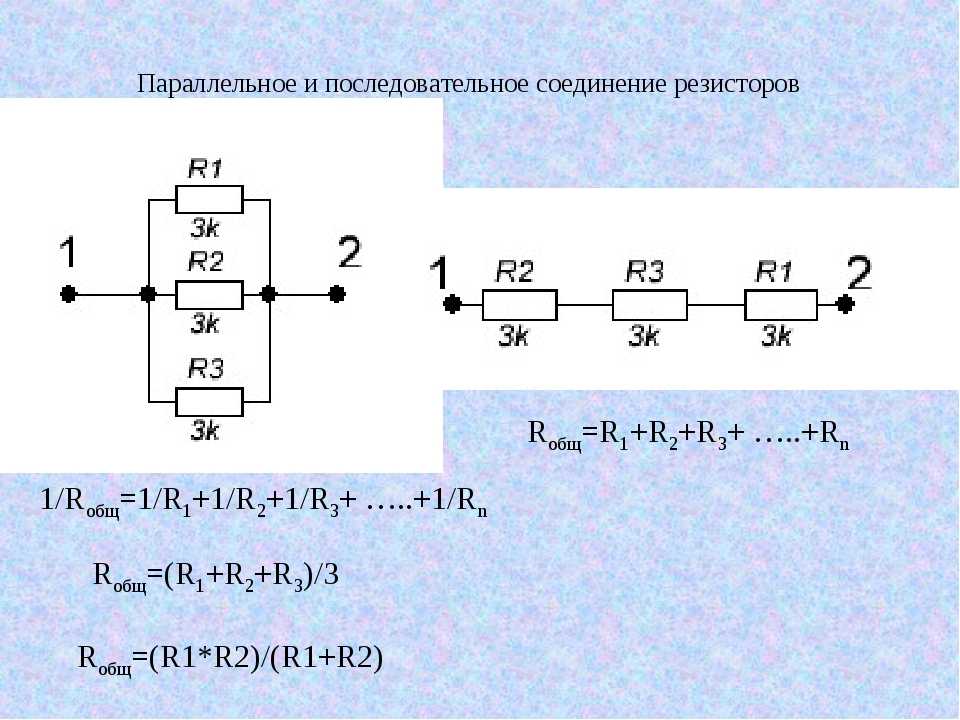
Параллельное соединение трубопроводов
Если протяженности ветвей равны друг
другу, т.е. ,
то речь идет о лупинге (от англ. loop – петля), широко используемом в практике
трубопроводного транспорта нефти по
магистральным трубопроводам.Рис. 9.11. Параллельное соединение трубопроводов
Система уравнений, определяющая движение жидкости в параллельных ветвях трубопроводной системы, такова:
(9.43)
Иными словами, при параллельном соединении двух трубопроводов расходы складываются, а потери напора в трубопроводах равны друг другу. В принятых обозначениях имеет место система уравнений:
(9.44)
где
.
Считая расход жидкости в точке разветвления заданным, получаем два уравнения
(9.45)
для
определения двух неизвестных: и .
Возможно несколько случаев.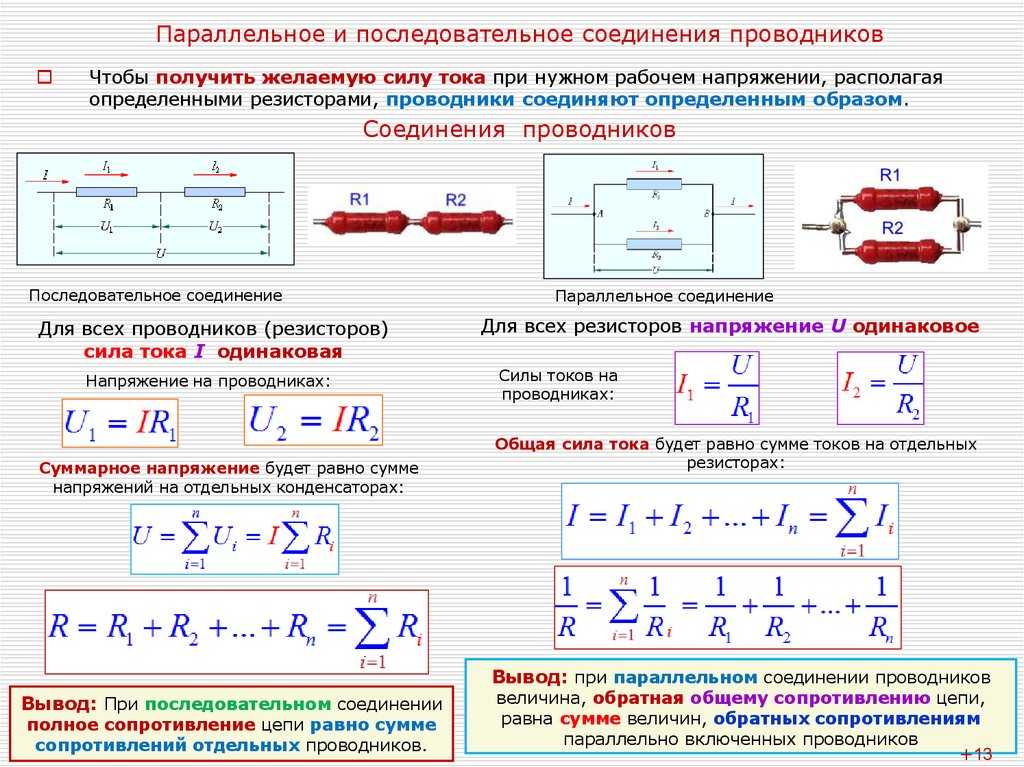
1) Если в каждой из параллельно соединенных труб режим движения жидкости ламинарный, то система уравнений (9.45) становится линейной:
Здесь использована формула (7.19) для потерь напора при ламинарном течении жидкости. Сокращая обе части второго уравнения на общий множитель, получаем:
(9.46)
Решение этой системы
определяет неизвестные расходы жидкости в каждом из параллельно соединенных трубопроводов.
После того, как расходы жидкости найдены, определяется потеря напора на участке 1-2:
(9.48)
Последнее равенство можно переписать в другой форме, а именно:
.
Полученный
результат аналогичен известному в
электротехнике правилу сложения
сопротивлений при параллельном соединении
проводников.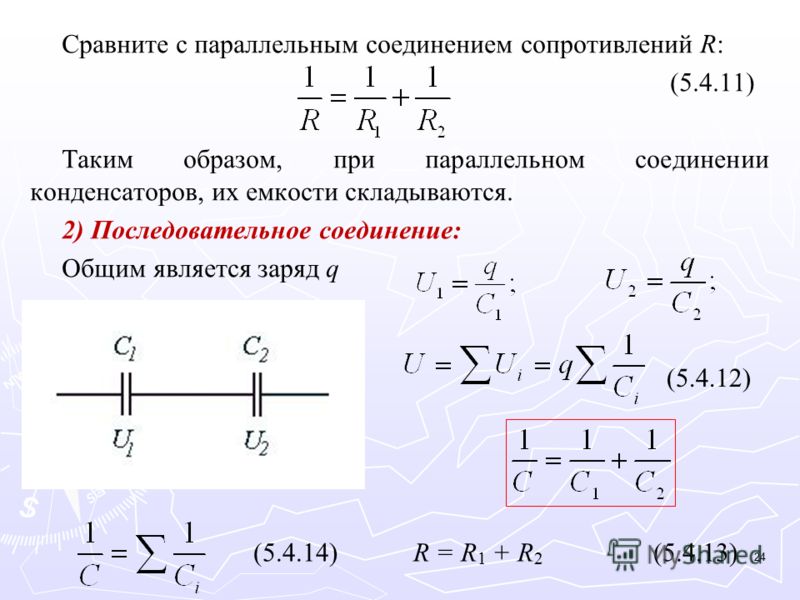
Действительно, при ламинарном
течении жидкости формула для гидравлического
сопротивления участка трубопровода
может быть записана в следующей форме:
Если величину по аналогии с электротехническими параметрами назвать сопротивлением трубопровода при ламинарном течении, а обратную ей величину — проводимостью, то формула (9. ) показывает, что при параллельном соединении трубопроводов проводимость участка равна сумме проводимостей отдельных составляющих его ветвей. Сопротивление всего участка 1-2 определяется формулой (9.48), которую можно записать так:
(9.49)
2) Рассмотрим другой предельный случай, при котором движение жидкости в каждой из параллельно соединенных труб — турбулентное, причем происходит в области квадратичного трения (см. п. 8.1): и константы.
Если обозначить , то получим систему линейных уравнений
(9.50)
для
определения расходов
и
в параллельных трубопроводах.
Разрешив
эту систему, найдем:
(9.51)
Потеря напора на участке 1-2 сложного трубопрвода находится как потеря напора в
(9.52)
Таким образом, если потери напора в каждом из простых трубопроводов выражаются формулами
и ,
то (9.52) означает, что такая же формула справедлива и для сложного трубопровода, полученного параллельным соединением простых трубопроводов, с той только разностью, что коэффициенты складываются.
3) В общем случае режимы течения жидкости в каждом из участков параллельно соединенных трубопроводов могут быть различными, поэтому коэффициенты и могут выражаться различными по виду формулами. Исключив из системы уравнений (9.45) один из расходов, например, , получим одно нелинейное уравнение
(9.
53)
относительно расхода . Для его решения необходимо использовать какой-либо численный метод, например, метод Ньютона или метод деления отрезка пополам [ ].
Можно использовать также графический способ. Этот способ решения уравнения (9.53) состоит в следующем. Задавшись набором значений расхода для течения жидкости в первой ветви , вычисляют соответствующие им скорости течения , затем числа Рейнольдса и, наконец, коэффициенты гидравлического сопротивления. Вслед за этим рассчитывают расходы жидкости во второй ветви сложного трубопровода , соответствующие им числа Рейнольдса и, наконец, коэффициенты гидравлического сопротивления. Построив график функции
находят координату точки его пересечения с осью . Значение есть искомое решение уравнения, причем есть расход жидкости во второй ветви трубопровода. После этого определяют потери напора на участке сложного трубопровода по формуле
.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
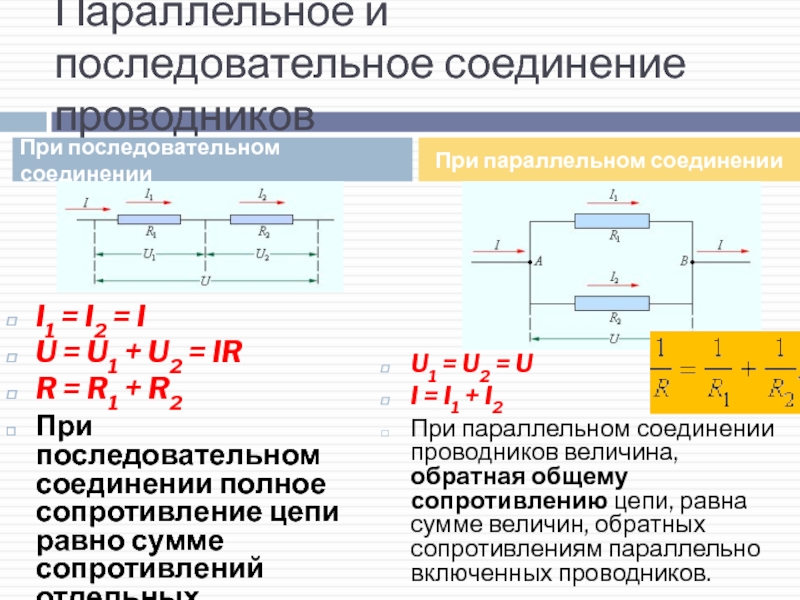
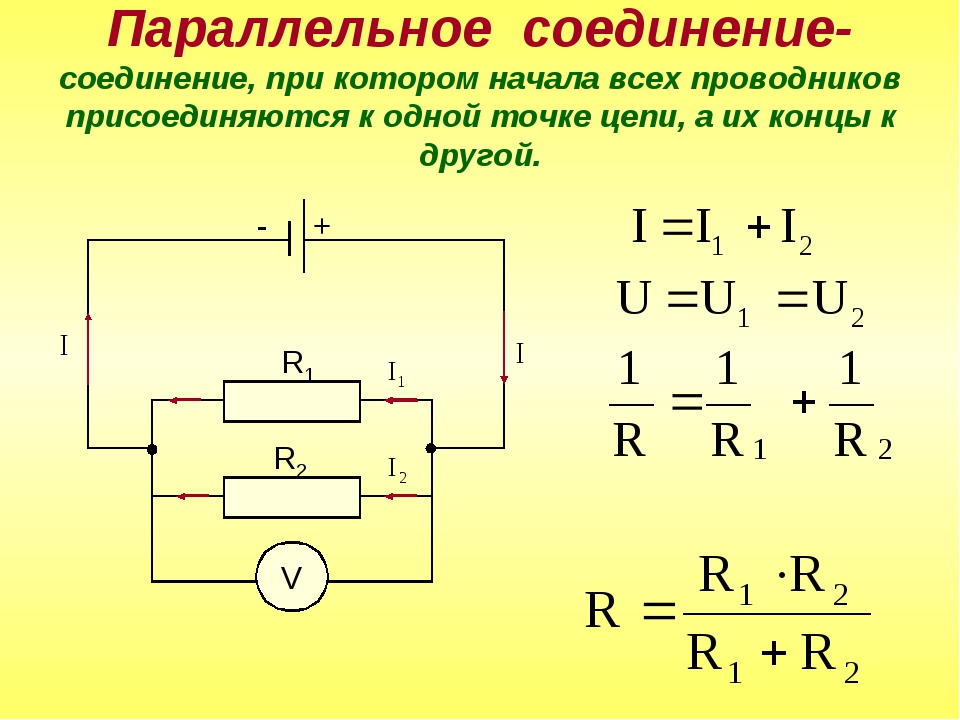
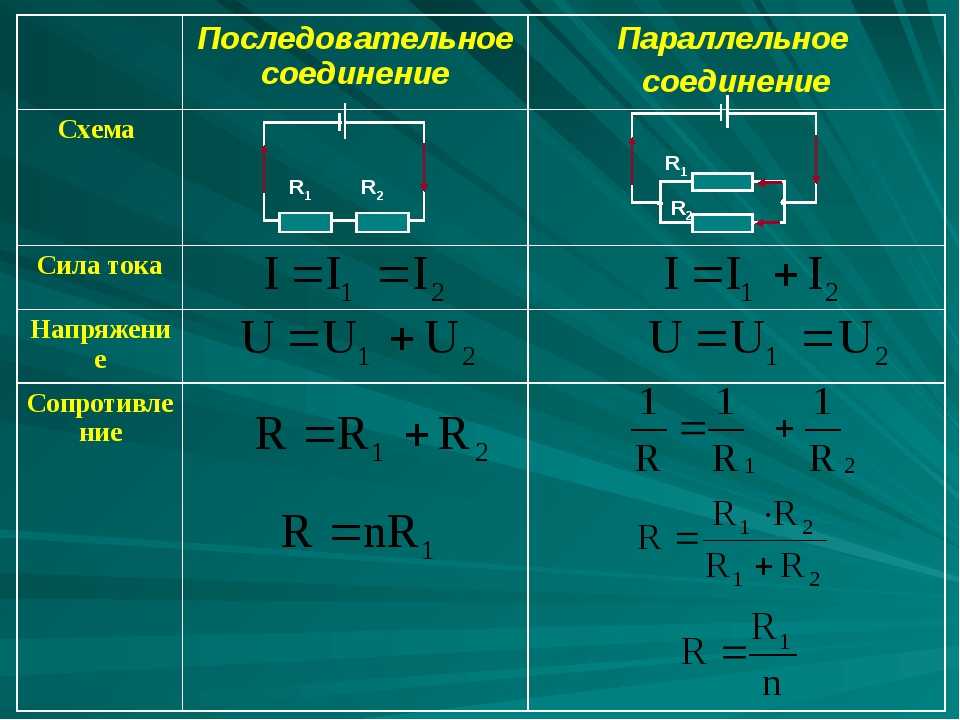
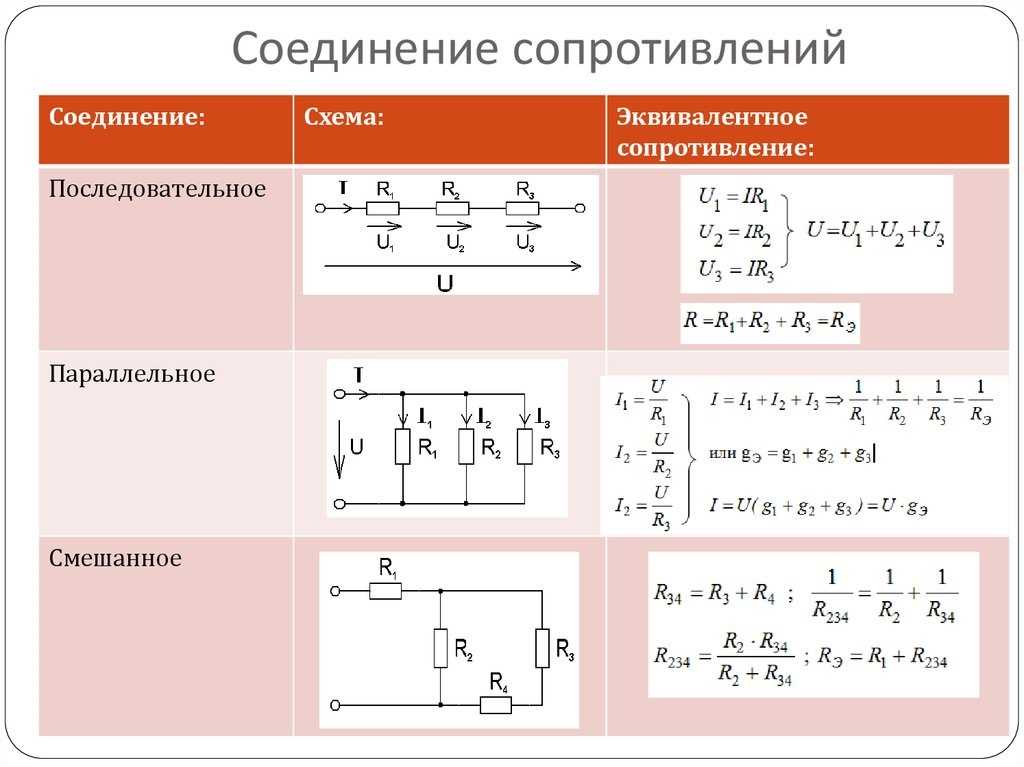
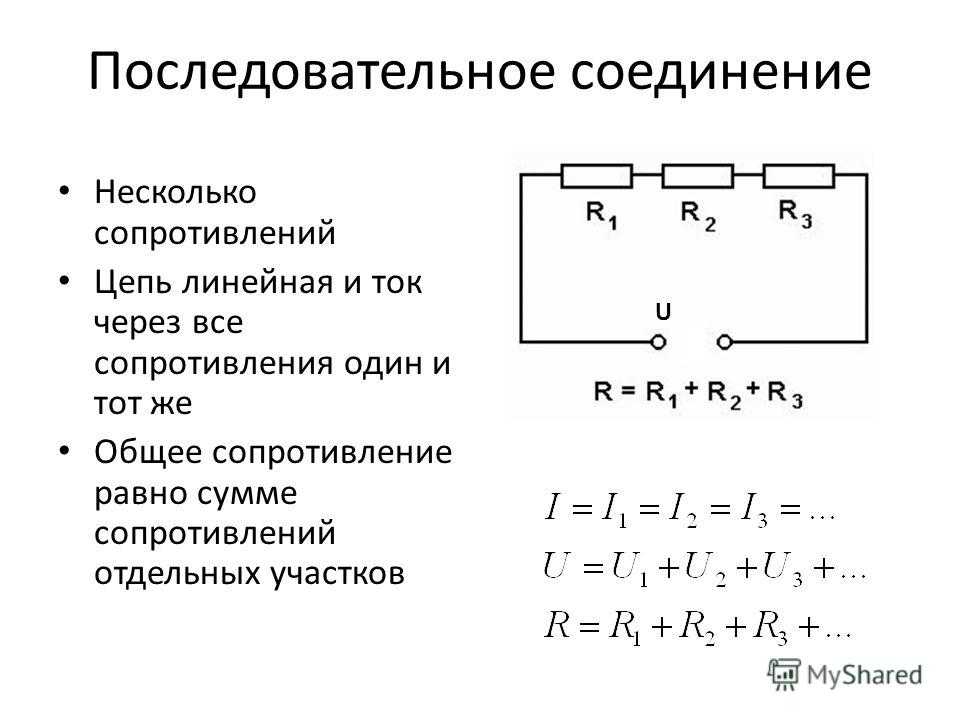
⇐ ПредыдущаяСтр 2 из 2 В этом случае все элементы подключаются к цепи друг за другом. Последовательное соединение не дает возможности получить разветвленную цепь — она будет неразветвленной. На рис. 1 показан пример последовательного соединения элементов в цепи.
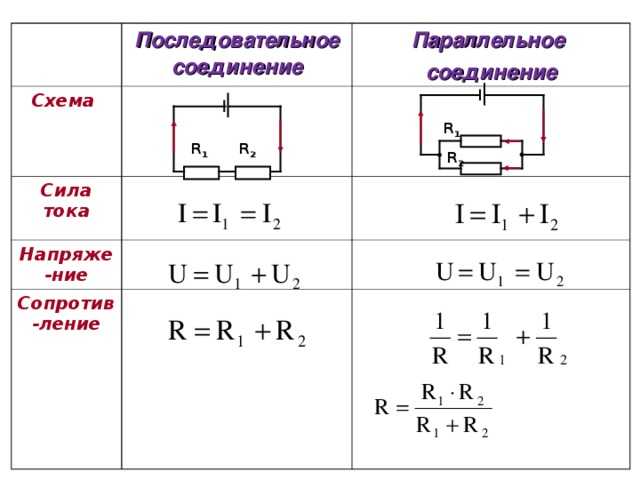
В нашем примере взяты два резистора. Резисторы 1 и 2 имеют сопротивления R1 и R2. Поскольку электрический заряд в этом случае не накапливается (постоянный ток), то при любом сечении проводника за определенный интервал времени проходит один и тот же заряд. Из этого вытекает, что сила тока в обоих резисторах равная: I = I1 = I2 А вот напряжение на их концах суммируется: U = U1 + U2 Согласно закону Ома, для всего участка цепи и для каждого резистора в отдельности полное сопротивление цепи будет: R = R1 + R2 В случае последовательного соединения проводников напряжения и сопротивления можно выразить соотношением: U1/U2 = R1/R2 БИЛЕТ 16 — Неразветвленная электрическая цепь постоянного тока. Неравзветвлённая ЭЦ (В неразветвленной цепи во всех ее элементах течет один и тот же ток.) Параллельное соединение проводников (Цепь разветвленная) Когда два проводника соединяются параллельно, электрическая цепь имеет два разветвления. Точки разветвления проводников называют узлами. В них электрический заряд не накапливается, т. е. электрический заряд, поступающий за определенный промежуток времени в узел, равен заряду, уходящему из узла за то же время. Из этого следует, что: I = I1 + I2 где I — сила тока в неразветвленной цепи. При параллельном соединении проводников напряжение на них будет одно и то же. Параллельное соединение проводников показано на рис. 2.
Обозначим сопротивления параллельно соединенных двух проводников R1 и R2. Используя закон Ома для участков электрической цепи с данными сопротивлениями, можно выявить, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных проводников, т. 1/R = 1/R1 + 1/R2 Из этого вытекает: R = R1R2/(R1 + R2) Данная формула справедлива только для определения общего сопротивления двух проводников, соединенных параллельно. Величину, обратную сопротивлению, называют проводимостью. При параллельном соединении проводников их сопротивления и сила тока связаны соотношением: I1/I2 = R2/R1
⇐ Предыдущая12 Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 902; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Все правила по сольфеджио
Параллельное соединение потребителей.
е.:
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)— Доказательство формулы для параллельных резисторов
Вопрос
Изменено 2 года, 2 месяца назад
Просмотрено 2к раз
\$\начало группы\$
В настоящее время я изучаю Искусство электроники , третье издание, Горовиц и Хилл. В упражнении 1.3 предлагается доказать формулы для последовательных и параллельных резисторов. Ранее в этой главе мне была дана следующая соответствующая информация:
- Сумма токов в точке цепи равна сумме выходных токов (сохранение заряда). Иногда его называют текущим законом Кирхгофа (KCL).
Инженеры любят называть такую точку узлом . Отсюда следует, что для последовательной цепи (куча двухполюсников, соединенных встык) ток везде одинаков.
- Вещи, соединенные параллельно (рис. 1.1), имеют одинаковое напряжение на них. В пересчете, сумма «падений напряжения» от A до B по одному пути через цепь равняется сумме по любому другому пути и представляет собой просто напряжение между A и B . Другими словами, сумма падений напряжения на любой замкнутой цепи равна нулю. Это закон напряжения Кирхгофа (KVL).
Инженеры любят называть такую точку узлом . Отсюда следует, что для последовательной цепи (куча двухполюсников, соединенных встык) ток везде одинаков. Я пытаюсь использовать эту информацию (и закон Ома \$V = IR\$, конечно) для доказательства параллельного случая \$R = \dfrac{R_1 R_2}{R_1 + R_2} \$. Однако я не понимаю, как предоставленной информации достаточно, чтобы сделать такой вывод.
Мне сказали, что это хороший учебник, так что, возможно, я просто новичок в электронике и поэтому чего-то не понимаю. Или, возможно, дело в том, что авторы не смогли предоставить достаточно информации для решения этой проблемы без внешних знаний.
Я был бы очень признателен, если бы люди нашли время, чтобы объяснить, как это можно сделать с помощью данной информации.
- анализ цепей
- резисторы
- сопротивление
- закон Ома
\$\конечная группа\$
4
\$\начало группы\$
AoE — это не особо теоретическая книга, это скорее практическое руководство с минимальным количеством математики, которое требуется для проведения анализа. «Хорошо» это или нет, зависит от ваших целей в изучении электроники.
В любом случае, если мы хотим заменить два резистора одним эквивалентным, мы можем рассчитать эквивалентный резистор по протекающему току. Принято считать, что напряжение на каждом резисторе одинаково.
Для R1 ток равен I1 = V/R1, для R2 ток I2 = V/R2, поэтому общий ток равен:
I1 + I2 = V(1/R1+1/R2) и наш «эквивалентный» резистор Rp = 1/(1/R1+1/R2) = R1R2/(R1+R2).
Добавление токов в узел: Ip — I1 — I2 = 0 (KCL), поэтому Ip = I1 + I2
\$\конечная группа\$
4
\$\начало группы\$
Возможно, будет легче понять, как это работает, если использовать обратное сопротивление — проводимость.
В параллельной цепи каждый компонент имеет одинаковое напряжение, поэтому ток, протекающий через него, не зависит от других. Общий ток — это сумма отдельных токов, поэтому общая проводимость — это просто сумма отдельных проводимостей.
Возьмем приведенный ниже пример:
смоделируйте эту схему — схема создана с помощью CircuitLab
R1 имеет проводимость 1/1 Ом = 1 А/В, R2 составляет 1/2 Ом = 0,5 А/В. , а R3 составляет 1/4 Ом = 0,25 А/В. Сложите их все вместе, чтобы получить общую проводимость 1,75 А/В, затем инвертируйте результат, чтобы получить общее сопротивление 1/1,75 = 0,571 Ом.
Это дает общую формулу для параллельных сопротивлений:-
\$\frac{1}{Rt} = \frac{1}{R1} + \frac{1}{R2} + …\frac{1 }{Rn}\$
В частном случае только двух резисторов, подключенных параллельно, вы можете изменить формулу из
\$\frac{1}{Rt} = \frac{1}{R1} + \frac{1 }{R2}\$
до
\$Rt = \frac{R_1 R_2}{R_1 + R_2}\$
\$\конечная группа\$
3
\$\начало группы\$
смоделируйте эту цепь. Схема создана с помощью CircuitLab
Общий ток в цепи будет равен It = V/Rt
Согласно KCL It = I1+I2, где I1 — ток, протекающий через резистор R1, а I2 — ток, протекающий через резистор R1. ток, протекающий через резистор R2.
Если подставить (закон Ома):
V/Rt = V1/R1+V2/R2. Но поскольку резисторы включены параллельно V1 = V2.
Но так как между источником напряжения и резисторами нет резистора V = V1 = V2.
V/Rt = V1/R1+V2/R2 -> V/Rt = V/R1+V/R2 и если мы разделим на V, мы получим 1/Rt = 1/R1 + 1/R2.
\$\конечная группа\$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Параллельные резисторы: уравнение, схема, расчеты, сети
Когда оба вывода резистора соединены с каждым выводом другого резистора или резисторов, говорят, что они соединены параллельно. В отличие от цепей с последовательными резисторами, поскольку в сети с параллельными резисторами имеется несколько каналов для тока, ток в цепи может проходить по нескольким путям. Затем делители тока применяются к параллельным цепям.
В этой статье вы получите представление о параллельных резисторах, их схеме, уравнении, расчетах, диаграмме, сетях, токе и некоторых примерах.
Подробнее: Понимание серийных резисторов
Содержание
- 1 Резисторы в параллельном
- 1.1. Быстрый пример расчета параллельного сопротивления:
- 1.2 Присоединение к нашему новостному бюллету
- 2 Согласно сети. 3 Цепь параллельных резисторов
- 4 Уравнение для параллельного резистора
- 5 Различные схемы резисторов при параллельном подключении
- 6 Резисторы при параллельном подключении Примеры расчета
- 6. 1 Пример № 1
- 6.2 Резисторы в параллельном соединении Пример № 2
- 6.2.1 Посмотрите видео ниже, чтобы узнать больше о параллельных резисторах:
- 6.
- No3
- 8.1 Эквивалентное сопротивление цепи:
- 9 Заключение
- 9.1 Пожалуйста, поделитесь!
1 Пример № 1Параллельное соединение резисторов
Если выводы двух резисторов подключены к одним и тем же двум узлам, они параллельны. Общее эквивалентное сопротивление меньше, чем у наименьшего параллельного резистора. Поскольку ток питания может проходить во многих направлениях, ток может быть неодинаков во всех ветвях параллельной сети. Однако в параллельной резистивной сети падение напряжения на всех резисторах одинаково. Тогда все параллельно соединенные элементы имеют общее напряжение на них, и это справедливо для всех параллельно соединенных резисторов.
Таким образом, параллельная резистивная цепь определяется как цепь, в которой резисторы подключены к одним и тем же двум точкам (или узлам), и отличается наличием нескольких токовых путей, соединенных с одним и тем же источником напряжения.
Напряжение на резисторе R1 равно напряжению на резисторе R2, которое равно напряжению на резисторе R3, равному напряжению питания в приведенном ниже примере с параллельным резистором.
Расчет эквивалентного сопротивления для резистора, включенного параллельно
Согласно приведенной ниже диаграмме, для формирования более сложных сетей резисторы часто соединяют последовательно или параллельно. На схеме выше вы можете увидеть пример параллельных резисторов. Каждый резистор в параллельной цепи имеет одинаковое напряжение. С другой стороны, ток обратно пропорционален сопротивлению каждого резистора. Эквивалентное сопротивление множества параллельных резисторов рассчитывается следующим образом:
1Req=n∑i=11Ri=1R1+1R2+⋯+1Rn1Req=∑i=1n1Ri=1R1+1R2+⋯+1Rn
Подробнее: Различные типы резисторов
Ток через каждый резистор определяется по формуле:
Ii=VRiIi=VRi
Краткий пример расчета параллельного сопротивления:
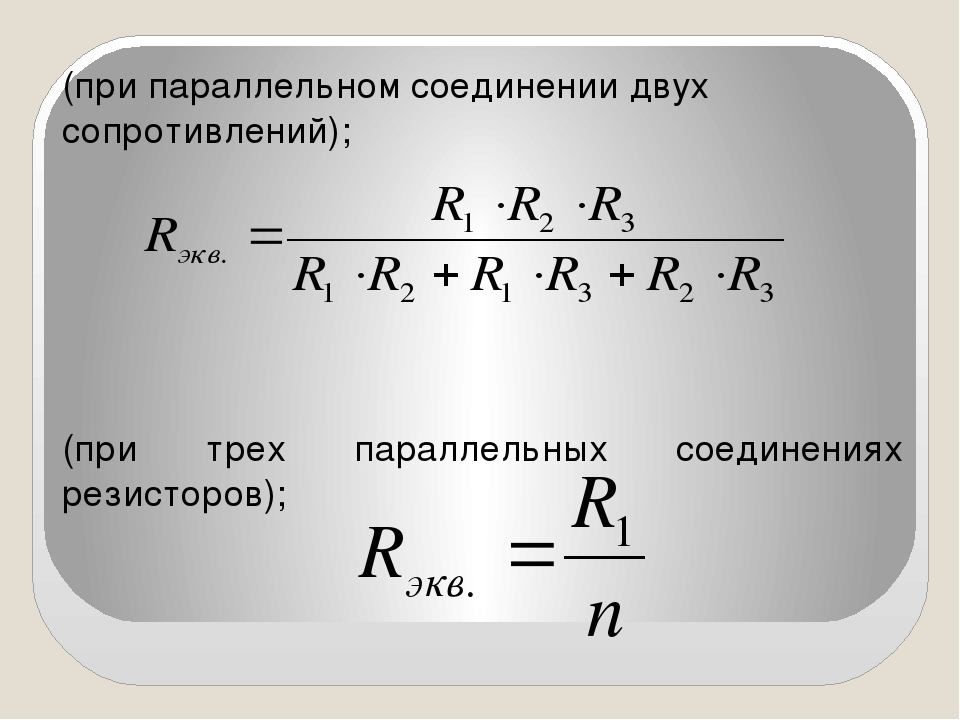
Разработчик схемы должен использовать резистор со значением 9 Ом и может выбирать из серии предпочтительных значений E-12 (…, 10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82, …).
Значение 9 Ом, к сожалению, недоступно в этой серии. Он решает построить аналогичное сопротивление 9Ом путем параллельного соединения двух стандартных значений. Эти процедуры используются для расчета эквивалентного значения сопротивления для двух параллельных резисторов: +R2R1⋅R21Req=R1+R2R1·R2
Req=R1⋅R2R1+R2Req=R1·R2R1+R2
Подробнее: Понимание металлооксидных пленочных резисторов
Приведенное выше уравнение пытается объяснить, что, если R1 равно R2, то Req составляет половину значения одного из двух резисторов. Для требования 9Ω, R1 и R2 должны иметь значение 2 x 9 = 18 Ω. Это стандартное значение для серии E.
Req=R1⋅R2R1+R2=18⋅1818+18=9ΩReq=R1·R2R1+R2=18·1818+18=9Ω эквивалентное сопротивление 9 Ом, как показано на диаграмме ниже.
Присоединяйтесь к нашему информационному бюллетеню
Решение сети с параллельными и последовательными резисторами
Методическое группирование резисторов обычно позволяет решать более сложные резисторные сети.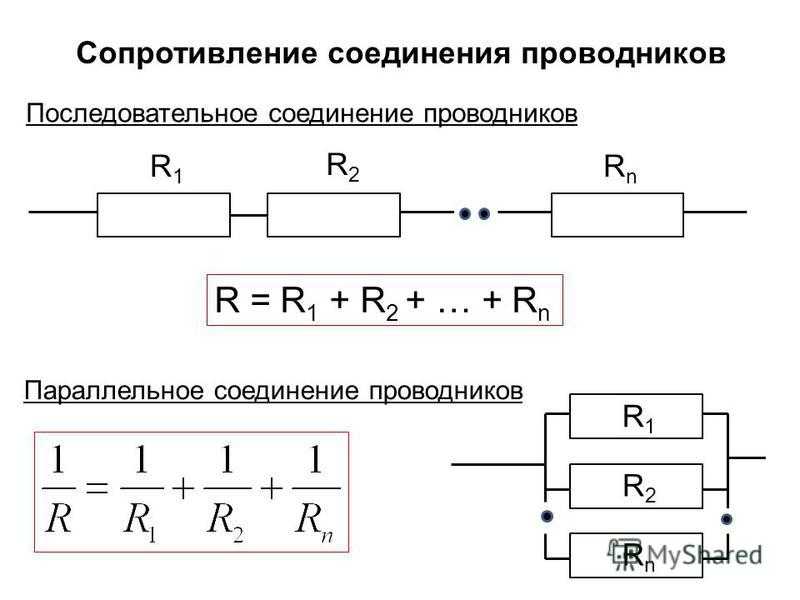
Три резистора соединены, как показано на левом изображении ниже. Резисторы R2 и R3 соединены последовательно. Они включены последовательно с резистором R1. Резисторы разделены на две группы для решения схемы, как показано на среднем изображении. R1 — единственный член группы 1. R2 и R3 составляют группу 2.
Сумма R2 и R3 может быть легко использована для вычисления эквивалентного сопротивления группы 2: параллельные резисторы. Эквивалентное сопротивление этой цепи вычисляется просто: +R3Req=R1·(R2+R3)R1+R2+R3
Подробнее: Знакомство с резисторами SMD (резисторы для поверхностного монтажа)
Более крупные сети могут быть решены путем повторного использования этих принципов для расчета параллельных и последовательных резисторов. Законы Кирхгофа применимы и к более сложным сетям. Резисторы R1, R2 и R3 подключены параллельно между двумя точками A и B в следующих резисторах в параллельной цепи.
Цепь параллельных резисторов
Общее сопротивление цепи последовательных резисторов, RT, равно сумме всех отдельных резисторов, сложенных вместе.
Эквивалентное сопротивление цепи RT рассчитывается по-разному для параллельных резисторов.
Вместо прямого сложения сопротивлений обратные (1/R) значения отдельных сопротивлений складываются вместе, при этом обратная алгебраическая сумма дает эквивалентное сопротивление, как указано.
Уравнение параллельного резистора
Алгебраическая сумма обратных величин отдельных сопротивлений является обратной величиной эквивалентного сопротивления двух или более резисторов, соединенных параллельно.
Подробнее: Что такое резисторы
Общее или эквивалентное сопротивление, RT, равно половине значения одного резистора, если два параллельных сопротивления или импеданса равны и имеют одинаковое значение. Р/2, Р/3, Р/4, Р/5, Р/6, Р/7, Р/8, Р/9, Р/10, Р/11, Р/12, Р/13, Р/ 14, R/15, R/16, R
Поскольку эквивалентное сопротивление всегда меньше наименьшего резистора в параллельной сети, при добавлении большего количества параллельных резисторов общее сопротивление RT всегда будет падать.
Параллельное сопротивление дает значение, известное как проводимость, символ G, с Сименсом, знак S, как единицу проводимости. (G = 1/R) Проводимость обратна или обратна сопротивлению. Чтобы преобразовать проводимость обратно в значение сопротивления, умножьте ее на обратную величину, что даст нам общее сопротивление RT параллельных резисторов.
Теперь мы знаем, что параллельные резисторы — это резисторы, подключенные между одними и теми же двумя точками. Однако параллельная резистивная цепь может иметь множество различных форм, кроме той, что показана выше, и ниже приведены некоторые примеры того, как резисторы могут быть соединены параллельно.
Различные схемы резисторов, включенные параллельно
Хотя пять приведенных ниже резистивных сетей кажутся разными, все они настроены как параллельные резисторы, поэтому применяются одни и те же требования и уравнения.
Примеры параллельного расчета резисторов
Пример № 1
Взгляните на приведенную ниже схему.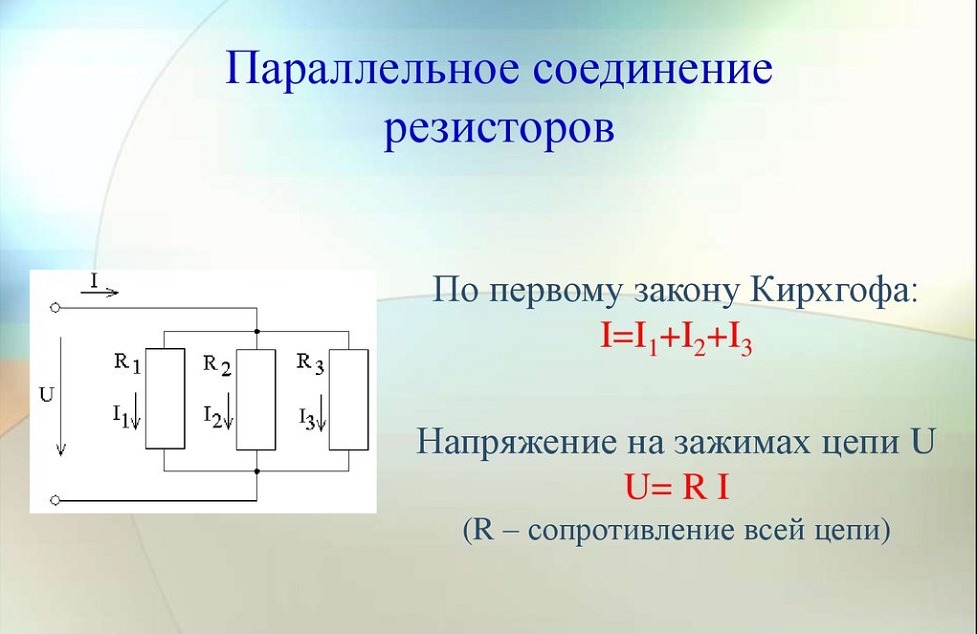
Рассчитайте общее сопротивление RT резисторов в следующей параллельной сети.
Общее сопротивление RT между A и B рассчитывается следующим образом:
Подробнее: Понимание термистора
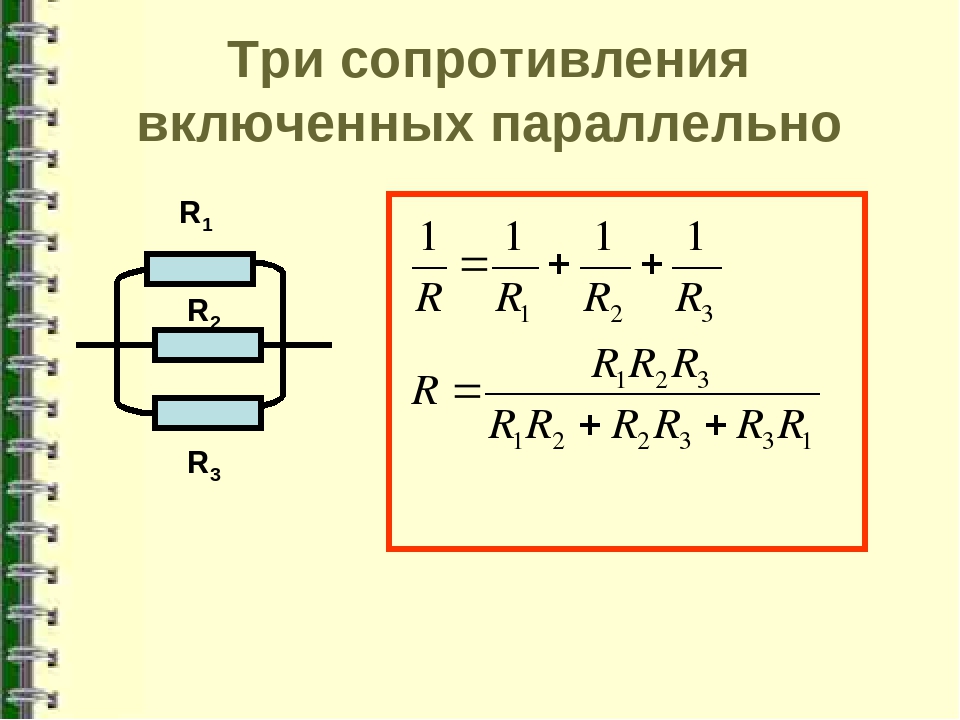
С помощью этого метода обратного расчета можно рассчитать любое количество отдельных сопротивлений, соединенных вместе в одной параллельной сети. .
Однако, если есть только два отдельных резистора, соединенных параллельно, мы можем определить общее или эквивалентное значение сопротивления, RT, используя гораздо более простую и быструю формулу, немного сократив обратные математические вычисления.
Ниже приведен значительно более быстрый способ вычисления двух резисторов, соединенных параллельно, с равными или неравными значениями, методом произведения на сумму:
Параллельные резисторы Пример №2 параллельная конфигурация.
Используя приведенную выше формулу для двух параллельно соединенных резисторов, общее сопротивление цепи R T можно рассчитать следующим образом: (RT) любых двух параллельно соединенных резисторов всегда МЕНЬШЕ, чем значение наименьшего резистора в комбинации.
Подробнее: Понимание варистора
Теперь давайте посмотрим на ток в цепи с параллельным резистором, что приведет нас к последнему примеру.
Посмотрите видео ниже, чтобы узнать больше о параллельных резисторах:
Это видео расскажет вам о расчетах параллельных резисторов:
Подробнее: Конденсатор
Токи сопротивления в цепи параллельного резистора
В параллельной цепи , общий ток I T представляет собой сумму всех отдельных токов, протекающих во всех параллельных ветвях.
Однако, поскольку значение сопротивления каждой ветви определяет величину тока, протекающего внутри этой ветви, величина тока, протекающего через каждую параллельную ветвь, может быть неодинаковой.
Несмотря на то, что параллельная комбинация имеет одинаковое напряжение на ней, сопротивления могут различаться, и, таким образом, ток, протекающий через каждый резистор, будет разным, как указано в законе Ома.
Рассмотрим два резистора, соединенных последовательно выше. Ток, протекающий через каждый из параллельно включенных резисторов (IR1 и IR2), не всегда одинаков, поскольку определяется сопротивлением резистора. Мы знаем, однако, что ток, входящий в цепь в точке А, должен также выйти в точке В.0005
Согласно законам тока Кирхгофа, «общий ток, выходящий из цепи, равен общему току, входящему в цепь — ток не теряется». В результате общий ток, протекающий в цепи, равен:
I T = I R1 + I R2
Используя закон Ома, ток, протекающий через каждый параллельный резистор в примере №2, можно рассчитать следующим образом.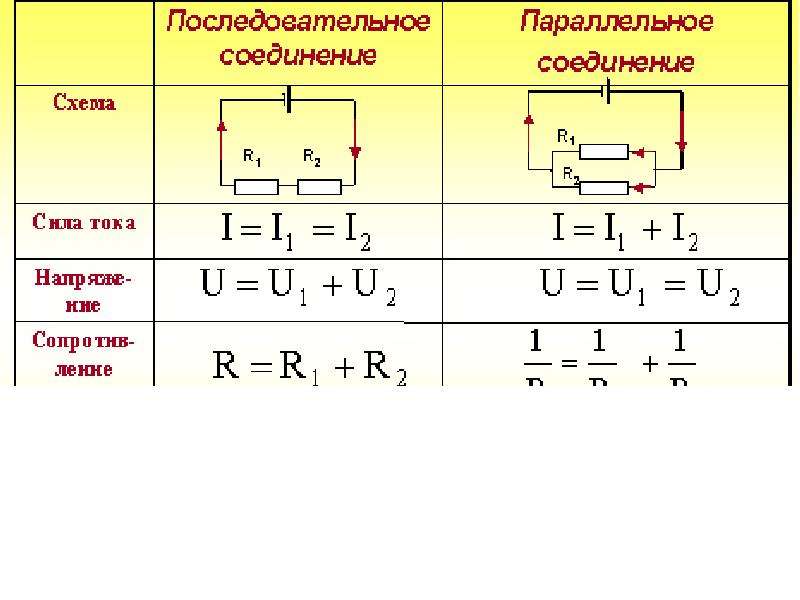
:
Ток, протекающий через резистор R1, рассчитывается следующим образом:
I R1 = V S ÷ R 1 = 12V ÷ 22KОм = 0,545 мА или 545 мкА
Происхождение через резистор R2 рассчитывается как:
I R2 = V S I R2 = V S . R2 = v S . R2 = V S 7. R2 = v S . R2 = v S 7. 2 7. = 12 В ÷ 47 кОм = 0,255 мА или 255 мкА Таким образом, общий ток I T , протекающий по цепи, равен: быть проверены непосредственно с помощью закона Ома как: I T = V S ÷ R T = 12 ÷ 15 кОм = 0,8 мА или 800 мкА (то же самое) Подробнее: Понимание ультраконденсаторов Ниже приведено уравнение для расчета полного тока, протекающего в цепи с параллельным резистором. который представляет собой сумму всех отдельных токов, объединенных вместе: I всего = I 1 + I 2 + I 3 …. многочисленные параллельные ответвления, параллельные сети резисторов также можно рассматривать как «делители тока». В результате параллельная цепь резисторов с N резистивными цепями будет иметь N токовых путей, сохраняя при этом общее напряжение между собой. Параллельные резисторы также можно заменять, не влияя на общее сопротивление или ток в цепи. Рассчитайте токи отдельных ветвей и общий ток, потребляемый от источника питания для следующего набора резисторов, соединенных параллельно, используя приведенную ниже диаграмму. Мы можем использовать закон Ома для определения тока отдельной ветви в параллельной цепи, потому что напряжение питания распределяется между всеми резисторами. Подробнее: Конденсаторы серии Полный ток цепи, I T , втекающий в параллельную комбинацию резисторов, будет тогда: Этот общий ток цепи, равный 5 амперам, также можно рассчитать и проверить, разделив напряжение питания VS на эквивалентное сопротивление цепи RT параллельной ответвляться. Тогда ток, протекающий в цепи, будет: Подробнее: Понимание параллельных конденсаторов Два или более резистора считаются соединенными параллельно, если оба их вывода соединены с каждым выводом другого резистора или резисторов. Напряжение на каждом резисторе в параллельной комбинации одинаково, но токи, протекающие через них, разные, как определяют их значения сопротивления и закон Ома. Тогда есть делители тока, которые представляют собой параллельные цепи. Это все для этой статьи, где обсуждаются схема, уравнение, расчеты, сети, ток и некоторые примеры параллельных резисторов. Я надеюсь, что вы получили много полезного от чтения, если да, пожалуйста, поделитесь с другими студентами. Спасибо за чтение, увидимся! Опубликовано Можно подумать, что если вам нужно конкретное сопротивление, вы найдете резистор с таким сопротивлением, и вам никогда не придется беспокоиться о соединении нескольких резисторов. Реальность такова, что параллельное или последовательное соединение резисторов чрезвычайно распространено, намеренно или в качестве побочного эффекта. От простых делителей напряжения до групп светодиодов, подключенных параллельно, вы найдете резисторы в комбинации практически везде. Когда резисторы соединены последовательно, это означает, что один резистор следует непосредственно за другим. Из двух узлов резистора один из этих узлов соединен с одним узлом другого резистора и больше ни с чем. Изображение поможет проиллюстрировать этот случай. Вы можете видеть, что если какое-либо электричество протекает через один из резисторов, ему некуда больше течь, кроме как через другой резистор. И если сопротивление не будет точно таким же, у вас будут разные напряжения на них. Давайте сделаем пример, чтобы показать, почему это так. При последовательном соединении двух резисторов мы получаем эквивалентное сопротивление 500 Ом — простое суммирование двух сопротивлений. Используя закон Ома, мы можем определить ток, протекающий через оба резистора. При 5 В на 500 Ом мы получаем 0,01 ампер или 10 миллиампер. Но затем, чтобы определить напряжение на каждом резисторе, мы снова используем закон Ома, но ищем зависимость напряжения от силы тока. Итак, умножаем ток на сопротивление. И, если у вас есть 1 В и 4 В, вы получите 5 В, давая нам тепло и нечетко, что мы сделали наши расчеты правильно. Итак, опять же, последовательно соединенные резисторы имеют одинаковый ток и, если они не имеют одинакового сопротивления, разные напряжения. Обратите внимание, что резисторы, соединенные последовательно, всегда имеют более высокое эквивалентное сопротивление. Когда резисторы соединены параллельно, это означает, что резисторы «разделяют» ток. Из двух узлов резистора оба этих узла подключены к обоим узлам другого резистора. Конечно, чтобы это имело какой-то смысл, эти узлы также *должны* быть подключены к чему-то еще — даже если это просто питание и земля. Поскольку оба узла подключены, видно, что напряжение на этих резисторах всегда будет одинаковым. Однако, поскольку они параллельны, если у них не одинаковое сопротивление, через них будут проходить разные токи. Чтобы найти эквивалентное сопротивление этих двух параллельно, можно было бы по отдельности рассчитать ток через резисторы, сложить этот ток вместе, а затем использовать закон Ома для расчета сопротивления, теперь, когда вы знаете напряжение и общий ток. Однако есть гораздо более простые способы сделать это, хотя это никогда не будет так просто, как с последовательными резисторами. Найти параллельное эквивалентное сопротивление не так уж и сложно, тем не менее мне удается сбить меня с толку, потому что я все еще умудряюсь забыть окончательную инверсию. Как видите, эквивалентность — это сумма обратных величин сопротивлений. И затем, как только эта сумма будет найдена, вы также инвертируете ее. Возможно, распространенная ошибка, или, может быть, просто то, с чем я сначала боролся, заключается в том, что я не забываю инвертировать это конечное число. Простой способ проверить это на работоспособность заключается в том, что если вы все сделали правильно, общее сопротивление будет ниже, чем самое низкое или наименьшее сопротивление включенных резисторов. Давайте сделаем образец, используя те же значения, которые мы использовали с последовательными резисторами. При этом мы добавляем 1/100 + 1/400 и получаем 1/80. Однако, если у вас есть только два резистора, вы можете использовать упрощенное уравнение для расчета эквивалентного сопротивления. А если два резистора одного номинала, то еще проще — делим сопротивление пополам! В противном случае вы можете использовать следующее уравнение: Вы можете соединить столько резисторов параллельно и последовательно, сколько хотите, ничто вас не остановит, хотя в какой-то момент это становится нелепым. И в качестве бонуса все это идеально подходит для катушек индуктивности, включенных параллельно и последовательно. Вот оно! Если что-то непонятно, напишите об этом в комментариях ниже, и мы либо ответим там, либо обновим этот учебник по мере необходимости. Если кто-нибудь даст мне схему, как я смогу определить, соединены ли резисторы последовательно или параллельно? При проверке последовательного или параллельного соединения резисторов необходимо помнить о двух вещах. Первое, что нужно помнить, это то, что очень часто резисторы не соединены последовательно или параллельно, но их взаимосвязь более сложна, и простые инструменты для нахождения эквивалентного сопротивления на самом деле не работают. Тем не менее, самый простой способ выяснить, соединены ли они последовательно или параллельно, и посмотреть, какой именно, — это посмотреть на два узла или на два конца каждого резистора. Если резисторы имеют один общий узел и к этому узлу больше ничего не подключено, то они соединены последовательно. Если у резисторов оба узла общие, даже если к этим узлам подключено что-то еще, то они параллельны. Если вы посмотрите на миниатюру этого видео, вы увидите, что на изображении слева параллельная конфигурация имеет оба конца (или оба узла) обоих резисторов, соединенных друг с другом. На правом изображении последовательная конфигурация имеет только один конец (или один узел) каждого резистора, соединенного вместе. 10 вопросов Интересуясь встраиваемыми системами, туризмом, кулинарией и чтением, Джош получил степень бакалавра электротехники в Университете штата Бойсе. Проработав несколько лет офицером CEC (Seabee) в ВМС США, Джош уволился и в конце концов начал работать над CircuitBread с кучей замечательных людей. Вопрос Если кто-нибудь даст мне схему, как я смогу определить, соединены ли резисторы последовательно или параллельно? A При проверке последовательного или параллельного соединения резисторов необходимо помнить о двух вещах. Первое, что нужно помнить, это то, что очень часто резисторы не соединены последовательно или параллельно, но их взаимосвязь более сложна, и простые инструменты для нахождения эквивалентного сопротивления на самом деле не работают. Тем не менее, самый простой способ выяснить, соединены ли они последовательно или параллельно, и посмотреть, какой именно, — это посмотреть на два узла или на два конца каждого резистора. Если резисторы имеют один общий узел и к этому узлу больше ничего не подключено, то они соединены последовательно. Если у резисторов оба узла общие, даже если к этим узлам подключено что-то еще, то они параллельны.2 I
R2 = V S2 I
R2 = V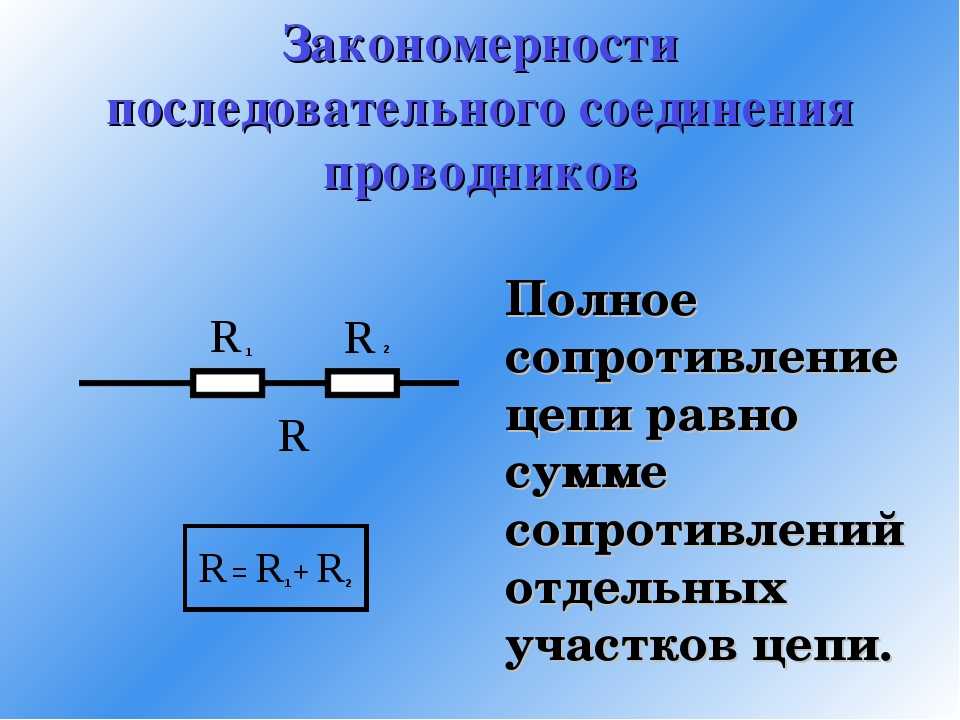
. + I n Параллельное соединение резисторов Пример №3
Эквивалентное сопротивление цепи:
Заключение
Как работают параллельные и последовательные резисторы?
youtube.com/embed/CRCZM6TLcFQ?rel=0″ frameborder=»0″ allow=»autoplay; encrypted-media» allowfullscreen=»»> Резисторы последовательно
Когда два резистора соединены последовательно, через них всегда проходит один и тот же ток. Таким образом, вы можете считать, что эквивалентное сопротивление двух последовательно соединенных резисторов представляет собой сумму отдельных сопротивлений.
Для резистора 100 Ом мы умножаем 0,01 на 100 Ом, что дает нам 1 В. Это означает, что в этой настройке резистор 100 Ом имеет 1 В на нем. Для резистора 400 Ом мы умножаем 0,01 на 400 Ом, что дает нам 4 В. Резисторы, соединенные параллельно
Изображение поможет проиллюстрировать, как выглядит простейший случай. Как найти параллельное эквивалентное сопротивление
Другими словами, вы находите параллельную эквивалентность, получая инверсию суммы инверсий. Поначалу это может показаться безумием, но взгляните на уравнение:
Получение обратной величины дает нам 80 Ом. Итак, эквивалентное сопротивление равно 80 Ом. Оно меньше, чем наименьшее сопротивление, поэтому мы можем чувствовать себя хорошо, по крайней мере, не слишком далеко. Если мы хотим, мы можем проверить, рассчитав общий ток, который проходит через комбинацию резисторов, а также резисторы по отдельности. 
Но *не* к конденсаторам! Резюме:
Упражнение
Автор:
Джош Бишоп
В настоящее время Джош живет на юге Айдахо с женой и четырьмя детьми. Часто задаваемые вопросы по учебнику
