Как рассчитать общее сопротивление при последовательном соединении резисторов. Какие существуют особенности параллельного соединения. Чем отличаются последовательные и параллельные цепи. Как решать задачи на смешанное соединение резисторов.
Последовательное соединение резисторов: принцип и расчет общего сопротивления
При последовательном соединении резисторов они подключаются друг за другом, образуя единую цепь. Главная особенность такого соединения заключается в том, что через все резисторы протекает одинаковый ток. Как рассчитать общее сопротивление при последовательном соединении? Для этого используется простая формула:
R = R1 + R2 + R3 + … + Rn
где R — общее сопротивление цепи, а R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Таким образом, при последовательном соединении общее сопротивление всегда больше сопротивления любого отдельного резистора в цепи. Это важное свойство, которое необходимо учитывать при проектировании электрических схем.
Параллельное соединение резисторов: особенности и расчет
При параллельном соединении все резисторы подключаются к одним и тем же точкам цепи. В этом случае напряжение на всех резисторах одинаково, а ток делится между ними. Как рассчитать общее сопротивление при параллельном соединении? Для этого используется следующая формула:
1/R = 1/R1 + 1/R2 + 1/R3 + … + 1/Rn
где R — общее сопротивление, а R1, R2, R3 и т.д. — сопротивления отдельных резисторов.
Важно отметить, что при параллельном соединении общее сопротивление всегда меньше сопротивления самого маленького резистора в цепи. Это свойство часто используется для снижения общего сопротивления цепи.
Сравнение последовательного и параллельного соединения резисторов
Чем отличаются последовательные и параллельные цепи? Основные различия заключаются в следующем:
- При последовательном соединении ток одинаков во всех элементах, а при параллельном — напряжение
- Общее сопротивление при последовательном соединении увеличивается, а при параллельном — уменьшается
- В последовательной цепи выход из строя одного элемента нарушает работу всей цепи, в параллельной — нет
- Параллельное соединение позволяет подключать больше потребителей к одному источнику питания
Понимание этих различий помогает правильно выбирать тип соединения при проектировании электрических схем.
Смешанное соединение резисторов: принципы расчета
На практике часто встречаются схемы со смешанным соединением резисторов, где присутствуют как последовательные, так и параллельные участки. Как решать задачи на смешанное соединение резисторов? Алгоритм решения следующий:
- Разбить схему на участки с однотипным соединением
- Рассчитать эквивалентное сопротивление для каждого участка
- Заменить участки эквивалентными резисторами
Этот метод позволяет решать даже сложные задачи, разбивая их на простые этапы.
Применение последовательного и параллельного соединения в электротехнике
Где используются различные типы соединений резисторов? Вот несколько примеров:
- Последовательное соединение применяется в делителях напряжения, измерительных приборах
- Параллельное соединение используется в бытовой электропроводке для подключения розеток
- В LED-светильниках часто используется смешанное соединение для управления яркостью
- В аккумуляторных батареях элементы могут соединяться как последовательно, так и параллельно
Правильный выбор типа соединения позволяет оптимизировать работу электрических устройств и систем.
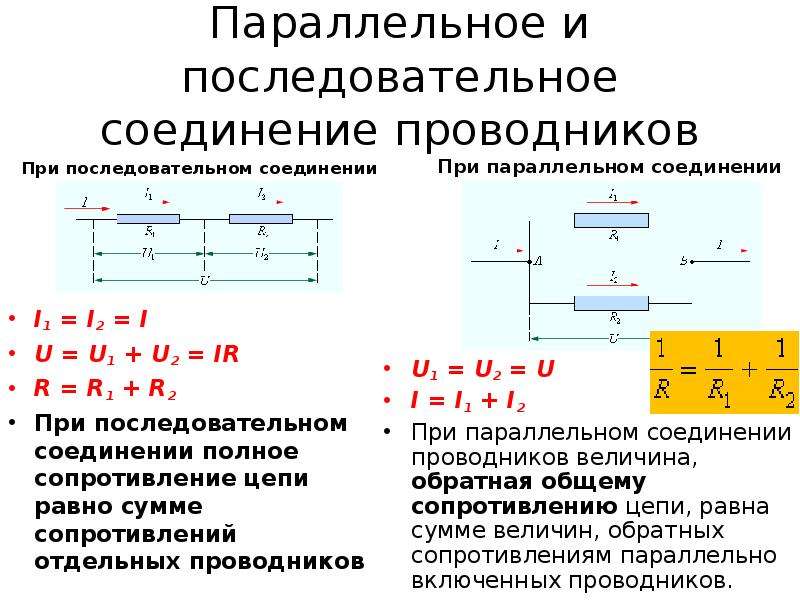
Законы Кирхгофа и их применение для анализа электрических цепей
Законы Кирхгофа являются фундаментальными принципами, используемыми для анализа электрических цепей. Как они помогают в расчетах сложных схем?
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Это позволяет составлять уравнения для токов в разветвленных цепях.
Второй закон Кирхгофа утверждает, что алгебраическая сумма напряжений в замкнутом контуре равна нулю. С его помощью можно анализировать распределение напряжений в цепи.
Применение законов Кирхгофа позволяет решать задачи для сложных электрических схем, которые нельзя свести к простому последовательному или параллельному соединению.
Практические задачи на расчет электрических цепей
Рассмотрим несколько типовых задач на расчет электрических цепей с резисторами:
Задача 1: Последовательное соединение
Три резистора с сопротивлениями 10 Ом, 20 Ом и 30 Ом соединены последовательно. Определите общее сопротивление цепи.
Решение: R = 10 + 20 + 30 = 60 Ом
Задача 2: Параллельное соединение
Два резистора с сопротивлениями 6 Ом и 3 Ом соединены параллельно. Найдите общее сопротивление.
Решение: 1/R = 1/6 + 1/3 = 1/2, откуда R = 2 Ом
Задача 3: Смешанное соединение
В схеме два резистора по 4 Ом соединены параллельно, а к ним последовательно подключен резистор 2 Ом. Определите общее сопротивление.
Решение: 1. Находим сопротивление параллельного участка: 1/R = 1/4 + 1/4 = 1/2, R = 2 Ом 2. Общее сопротивление: R = 2 + 2 = 4 Ом
Решение подобных задач помогает лучше понять принципы работы электрических цепей и развить навыки анализа схем.
Последовательное соединение резисторов. Схема соединения и примеры расчета
Главная » Справочник » Последовательное соединение резисторов. Схема соединения и примеры расчета
Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.
Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:
R = R1 + R2 + R3
То есть, в нашем случае общее сопротивление цепи будет равно:
R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм
Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.
Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.
Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).
Инвертор 12 В/ 220 В
Инвертор с чистой синусоидой, может обеспечивать питание переменно…
Подробнее
Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:
Используя закон Ома для участка цепи, напряжение на отдельных резисторов может быть вычислена следующим образом:
В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.
В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
Необходимо рассчитать падение напряжения на выводах «А» и «В»:
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Подробнее
Параллельное и последовательное соединение резисторов
В схемах используется параллельное, последовательное и смешанное подключение резисторов.
Необходимо помнить, что ток будет протекать по пути наименьшего сопротивления.
Содержание
- Последовательное соединение
- Параллельно сопротивление
- Калькулятор параллельного соединения резисторов
Последовательное соединение
При последовательном соединении общее сопротивление увеличивается. Общее сопротивление будет выше, чем сопротивление любого из резисторов.На всем участке цепи течет один и тот же ток, а общее сопротивление равно сумме всех сопротивлений. Для вычисления значения общего сопротивления необходимо к сопротивлению первого резистора прибавить сопротивление второго, третьего, четвертого резистора.
Rобщ = R1 + R2 + R3 + Rn
Например: R1 = 2 Om + R2 = 3 Om + R3 = 1 oM
Rобщ = 6 Om.
Другими словами:
При последовательном соединении резисторов их сопротивление складывается и общее сопротивление будет равно сумме R1 + R2 + R3…….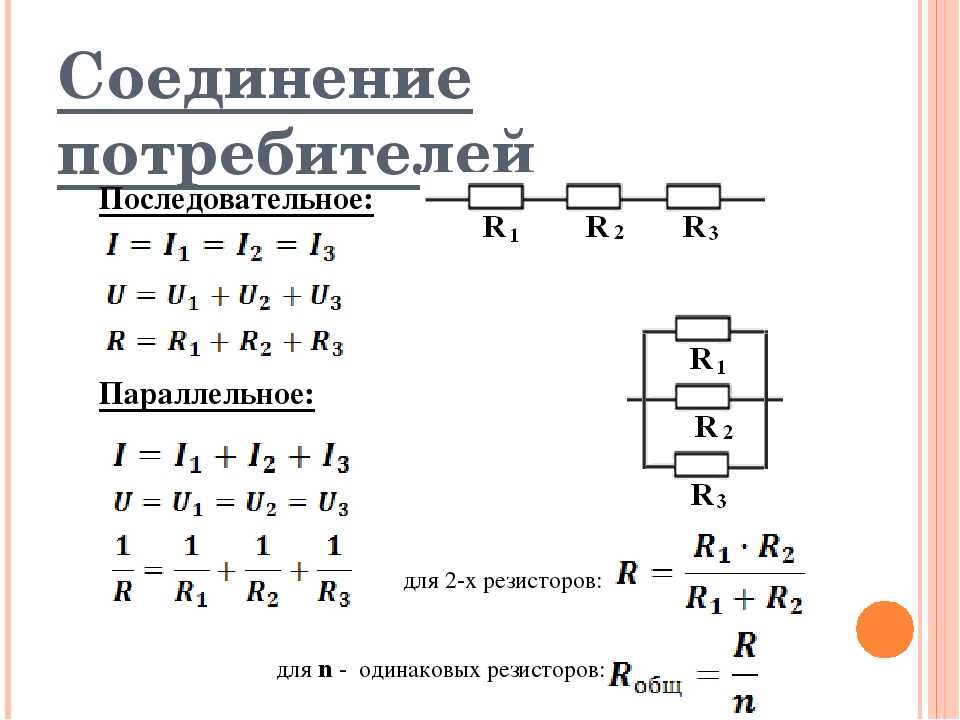
Параллельно сопротивление
При параллельном соединении общее сопротивление уменьшается. Общее сопротивление будет ниже, чем сопротивление любого из резисторов.При параллельном подключении резисторов, все немного интересней: Общее сопротивление всегда будет меньшим, чем значение наименьшего сопротивления в этой комбинации.
К каждому резистору при параллельном их соединении приложено одно и то же напряжение. А если сопротивлений резисторов в цепи при параллельном их соединении может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (в соответствии с законом Ома).
Для расчета общего сопротивления резисторов подключенных параллельно можно воспользоваться одной из следующих формул:
- Для нескольких параллельно соединенных резисторов с одинаковым номиналом:
\[ Rобщ = \frac{\color{red}R}{\color{blue}N} \]
\( Rобщ \) = общее сопротивление цепи или всех резисторов\( R \) = Номинал любого из резисторов
Предположим мы имеем 2 резистора соединенных параллельно.
Номинал каждого из которых равен 10 Ом.
Номинал каждого из которых равен 10 Ом.\[ Rобщ = ? \]
Исходя из формулы:
\[ Rобщ = \frac{\color{red}Rлюбого из резисторов = 10 Om}{\color{blue}2} \]
\[ Rобщ = 5 \]
Для нескольких параллельно соединенных резисторов с разным номиналом:
\[ \frac{1}{\color{red}R} = \frac{1}{\color{red}R1} + \frac{1}{\color{red}R2} +…+ \frac{1}{\color{red}Rn} \]
Калькулятор параллельного соединения резисторов
admin Учебник Leave a comment
Цепи серии
Представьте себе электрический ток, выходящий из батареи. Если резисторы соединены таким таким образом, чтобы часть тока могла проходить через один резистор, а остальные ток может идти через другой резистор, тогда цепь будет параллельной цепь .
I Т — полный ток параллельной цепи. Вы бы измерили этот ток
в любом месте до или после трехстороннего разделения, ведущего к трем резисторам. В
между перекрестком и R
Поскольку общий ток, I T , делится на три разные группы электроны, каждый из которых движется своим путем,
I T = Я 1 + Я 2 + я 3 +.
В параллельных цепях все
резисторы, независимо от их сопротивлений, испытывают одинаковое падение напряжения или
потенциальная разница, потому что все они имеют одинаковые точки входа и выхода
(соединения).
В Т = В 1 = В 2 = В 3 =V n
Если разделить формулу тока по зависимости напряжения получаем:
или R T = [Р 1 -1 + Р 2 -1 + Р 3 -1 + ] -1
|
а. Чему равно полное сопротивление цепи?
Р Т = [R 1 -1 + R 2 -1 + R 3 -1 ] -1
2 R 9 [12 -1 + 12 -1 +12 -1 ] -1 = 4 Вт б.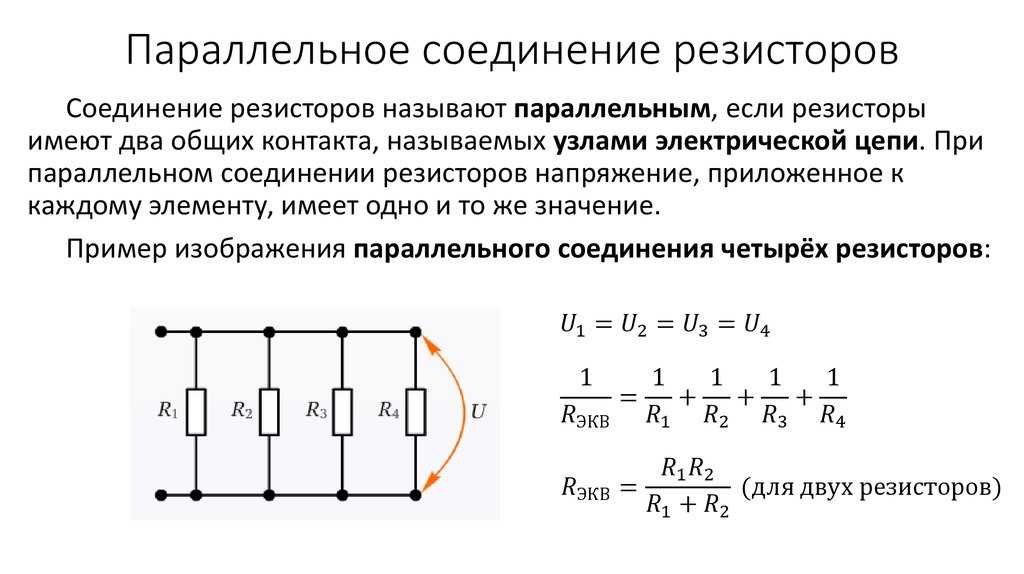
Каков общий ток?
I T = V/R T = 12/4 = 3 А
c. Какое напряжение (В 1 ) будет измеряется на каждом отдельном резисторе?
12 В (Напряжение параллельное постоянное.)
c. Какой ток потребляет каждый резистор?
I 1 = V/R 1 = 12/12 = 1 А. Остальные также по 1 А каждый, всего 3А.
Пример 2
рисунок кажется запутанным, но обратите внимание, что это параллельная цепь, потому что у электрона есть выбор. На стыке (показан красной точкой) электроны либо следуйте по зеленому маршруту, либо по оранжевому маршруту.
Применение I
1 = 1А; I 2 = 0,5 А; Р 1 = 10 Вт.
- Найти V 2 .
Помните, что параллельное напряжение постоянно. Итак, если мы найдем V 1 ,
мы будем знать V 2 .
В 1 = I 1 R 1 = 1(10) = 10 В. 02
- Найти R 2 .
R 2 = V/I 2 = 10/0,5 = 20 Вт.
- Используйте два метода для получения R T .
(1) Р Т = [Ч 1 -1 + R 2 -1 ] -1 = [20 -1 + 10 -1 ] -1 = 6,7 Вт.
(2) I T = I 3 = I 1 + I 2 = 1 + 0,5 = 1,5 A 0005 Вт
Пример 3
Какой эффект в параллельной схеме дает добавление еще резисторов есть на общий ток?
Текущее увеличение !
В схеме серии добавление дополнительных резисторов увеличивает
полное сопротивление и, таким образом, снижает ток.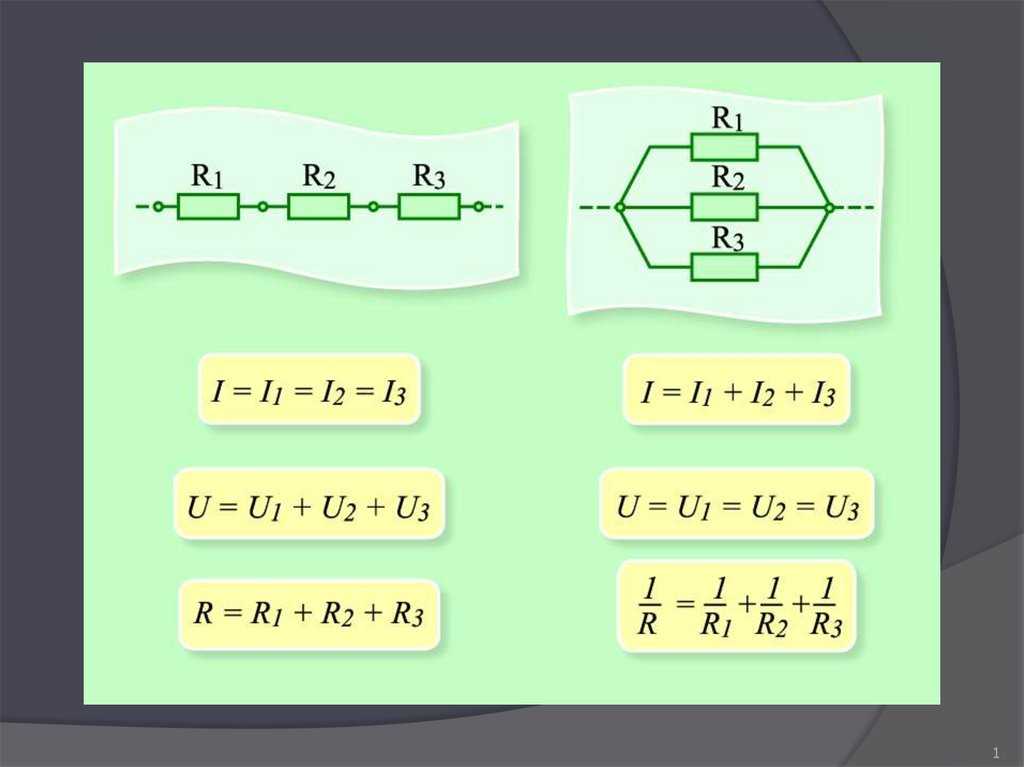
Но обратное верно в
параллельная схема, потому что добавление большего количества резисторов параллельно создает больше вариантов
и снижает общее сопротивление. Если тот же аккумулятор подключен к
резисторы, ток увеличится. Не убежден? Попробуйте:
[10 -1 + 10 -1 ] -1 = 5 Вт, но добавить резистор параллельно, и вы получите [10 -1 + 10 -1 + 10 -1 ] -1 = всего 3,3 Вт. меньшее сопротивление, вы столкнулись с более высоким общим током.
Еще одна интересная особенность параллельных цепей заключается в том, что если один компонент выключен, другие пути остаются жизнеспособными, так что электроны могут продолжать течь по цепи. Это причина того, что большинство ламп и розеток в доме подключены параллельно.
Как рассчитать общее сопротивление последовательной цепи?
от Veerendra
Как рассчитать общее сопротивление последовательной цепи?
Эффективное сопротивление последовательно соединенных резисторов
- В последовательной цепи есть три важные характеристики :
(а) Ток, проходящий через каждый резистор, одинаков.
(b) Разность потенциалов на каждом резисторе напрямую зависит от его сопротивления.
(c) Сумма разности потенциалов на каждом резисторе равна полной разности потенциалов источника. - Когда два или более сопротивления соединены встык так, что через каждое из них протекает одинаковый ток, говорят, что они соединены последовательно. Когда к батарее подключена последовательная комбинация сопротивлений, через каждое из них протекает одинаковый ток (I).
Когда к батарее подключена последовательная комбинация сопротивлений, через каждое из них протекает одинаковый ток (I). - Закон последовательного соединения сопротивлений: Закон последовательного соединения сопротивлений гласит, что при последовательном соединении нескольких сопротивлений их эквивалентное сопротивление равно сумме сопротивлений отдельных элементов. Таким образом, если R 1 , R 2 , R 3 … и т. д. соединены последовательно, то эквивалентное сопротивление (R) определяется выражением
R = R 1 + R 2 + R 3 + … …. (и) - Вывод математического выражения сопротивлений при последовательном соединении :
Пусть, R 1 , R 2 и R 3 — сопротивления, соединенные последовательно, I — ток, протекающий по цепи, т. е. проходящий через каждое сопротивление, а V 1 , V 2 и V 3 — разность потенциалов на R 1 , R 2 и R 3 соответственно. Тогда по закону Ома
В 1 = IR 9(ii) - + V 2 + V 3 … (iv)
- Используя уравнения (i)–(iv), мы можем написать ,
ИК = V = V 1 + V 2 + V 3
IR = IR 1 + IR 2 + IR 3
IR = I (R 1 0017 + Р 3 )
R = R 1 + R 2 + R 3
Следовательно, при последовательном соединении сопротивлений эквивалентное сопротивление выше, чем сопротивление каждого отдельного. - Эквивалентная схема показана на рис.
(и)
Некоторые результаты о комбинации серий:
- Когда два или более резистора соединены последовательно, общее сопротивление комбинации равно сумме всех сопротивлений по отдельности.
- Когда два или более резистора соединены последовательно, через каждый резистор протекает одинаковый ток.
- Когда несколько резисторов соединены последовательно, напряжение на комбинации
(т. е. напряжение батареи в цепи) равно сумме падения напряжения
(или разности потенциалов) на каждом отдельном резисторе.
Люди также спрашивают
- Чем отличаются последовательные и параллельные цепи?
- Как рассчитать общее сопротивление параллельной цепи?
- Что такое электрический ток?
- Что такое электрическое поле и как оно создается?
- Какая связь между электрическим током и разностью потенциалов?
- Электродвижущая сила, внутреннее сопротивление и разность потенциалов элемента/батареи
- Взаимосвязь между передаваемой энергией, током, напряжением и временем
- Power Rating and Energy Consumption of Various Electrical Appliances
- Three resistors, R 1 , R 2 and R 3 , are connected in series to a 6 V аккумулятор, как показано на рисунке.
Вычислите
(a) эффективное сопротивление R цепи,
(b) ток I в цепи,
(c) разность потенциалов на каждом резисторе, В 1 , В 2 и V 3 .
Решение:
Обратите внимание, что чем больше сопротивление, тем больше разность потенциалов на нем. Сумма разности потенциалов на каждом резисторе равна разности потенциалов на батарее.
Рубрики: Физика С тегами: рабочий лист комбинированных цепей с ответами, задачи сложных последовательных и параллельных цепей, последовательный и параллельный ток, вывод последовательностей, формула эффективного сопротивления, электричество, определение эквивалентного сопротивления, задачи эквивалентного сопротивления, Как рассчитать общее сопротивление последовательной цепи ?, как найти эквивалентное сопротивление, как решить задачи последовательно-параллельной цепи, определение параллельной цепи, примеры параллельных цепей, задачи с параллельными цепями с решениями, резисторы в последовательном и параллельном, последовательном и параллельном проблемы с цепями и ответы, определение последовательной цепи, схема последовательной цепи, проблемы с последовательной цепью с решениями, последовательная цепь против параллельной цепи.
