Что такое дискретный сигнал. Как происходит преобразование аналогового сигнала в дискретный. Какие виды дискретных сигналов существуют. Для чего используется дискретизация сигналов в цифровой электронике.
Что такое дискретный сигнал и его основные характеристики
Дискретный сигнал — это сигнал, значения которого определены только для отдельных моментов времени, называемых отсчетами. В отличие от непрерывного (аналогового) сигнала, дискретный сигнал имеет прерывистый характер и может принимать только конечное число значений.
Основные характеристики дискретного сигнала:
- Дискретность по времени — значения определены только для фиксированных моментов времени
- Дискретность по уровню — сигнал может принимать только определенные значения из конечного набора
- Период дискретизации — интервал времени между соседними отсчетами
- Частота дискретизации — число отсчетов в единицу времени
- Разрядность — количество битов, используемых для представления значения сигнала
Процесс преобразования аналогового сигнала в дискретный
Преобразование непрерывного аналогового сигнала в дискретный происходит в два этапа:
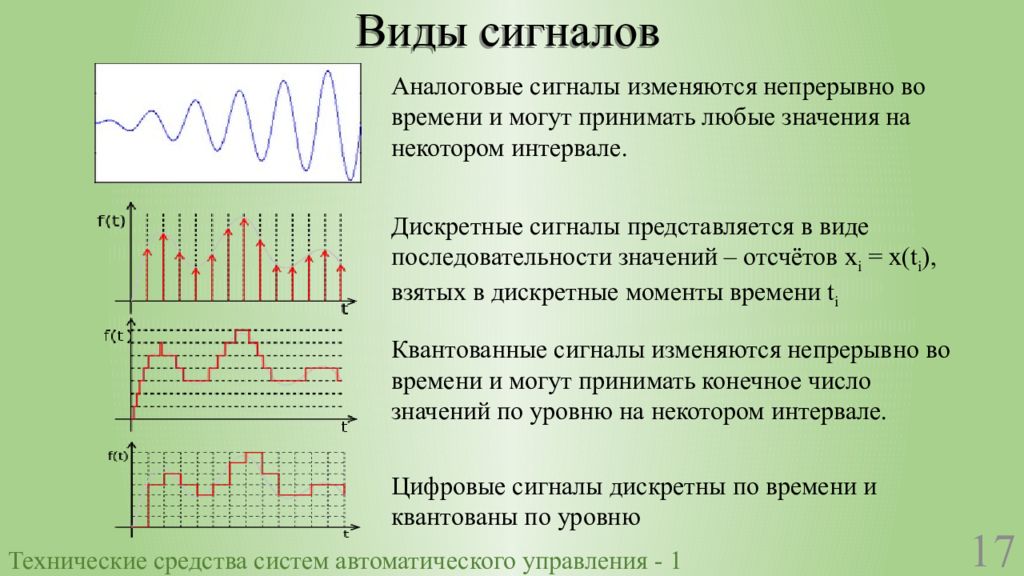
- Дискретизация по времени — взятие отсчетов сигнала через равные промежутки времени
- Квантование по уровню — округление значений отсчетов до ближайшего разрешенного уровня
Этот процесс называется аналого-цифровым преобразованием и выполняется с помощью АЦП (аналого-цифрового преобразователя). Ключевые параметры АЦП — частота дискретизации и разрядность квантования.
Основные виды дискретных сигналов
Можно выделить следующие основные виды дискретных сигналов:
- Импульсные сигналы — последовательность импульсов определенной формы
- Цифровые сигналы — последовательность двоичных значений (0 и 1)
- Кодово-импульсные сигналы — импульсы, модулированные по какому-либо параметру
- Дискретизированные аналоговые сигналы — отсчеты непрерывного сигнала
Применение дискретных сигналов в цифровой обработке
Дискретные сигналы широко используются в современной цифровой электронике и обработке информации:
- Цифровая обработка сигналов (фильтрация, спектральный анализ и др.)
- Цифровая связь и передача данных
- Цифровое аудио и видео
- Системы управления и автоматики
- Измерительная техника
Преимущества использования дискретных сигналов:
- Высокая помехоустойчивость
- Возможность сложной математической обработки
- Простота хранения и передачи информации
- Точность представления данных
Дискретизация сигналов по теореме Котельникова
Теорема Котельникова (теорема отсчетов) определяет условия, при которых дискретный сигнал полностью описывает исходный непрерывный сигнал. Согласно теореме, частота дискретизации должна как минимум в 2 раза превышать максимальную частоту в спектре исходного сигнала:
Fд ≥ 2Fмакс
где Fд — частота дискретизации, Fмакс — максимальная частота в спектре сигнала.
Это условие позволяет избежать наложения спектров (эффекта элайзинга) и обеспечить точное восстановление сигнала.
Квантование дискретных сигналов по уровню
Квантование — это процесс округления значений отсчетов до ближайших разрешенных уровней. Основные характеристики квантования:
- Шаг квантования — расстояние между соседними уровнями
- Число уровней квантования — определяется разрядностью АЦП
- Ошибка квантования — разность между исходным и квантованным значением
Чем меньше шаг квантования и больше число уровней, тем точнее представление сигнала, но больше требуемый объем памяти.
Восстановление аналогового сигнала из дискретного
Восстановление непрерывного сигнала из дискретного производится с помощью ЦАП (цифро-аналогового преобразователя) и включает следующие этапы:
- Формирование ступенчатого сигнала по отсчетам
- Сглаживание ступенчатого сигнала с помощью фильтра нижних частот
Качество восстановления зависит от частоты дискретизации, разрядности квантования и параметров сглаживающего фильтра.
Преимущества цифровой обработки дискретных сигналов
Использование дискретных сигналов и их цифровая обработка имеют ряд важных преимуществ:
- Высокая точность и стабильность характеристик
- Гибкость и универсальность алгоритмов обработки
- Возможность реализации сложных математических операций
- Помехоустойчивость при хранении и передаче данных
- Простота изменения параметров обработки
- Миниатюризация устройств обработки сигналов
Эти преимущества обусловили широкое распространение цифровых методов обработки сигналов в современной электронике и информационных технологиях.
Примеры непрерывных дискретных сигналов. Дискретный сигнал
Содержание
- Дискретность – это …
- Что такое дискретный
- Примеры простейшей дискретности
- Особенности непрерывного сигнала
- Формы представления дискретной информации
- Этапы дискретизации
- Что такое аналоговый сигнал
- Что такое цифровой сигнал
- В чем разница между аналоговым и цифровым сигналом
- Преимущества и недостатки сигналов разных видов
- Что такое аналоговая электроника?
- Преобразование сигнала
Дискретность – это …
Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.
В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.
Дискре́тность (от лат.
discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:
Дискретность можно толковать следующим образом:
- как меняющееся состояние между двумя и более стабильными положениями. К примеру, качающийся маятник: достигает точки А, затем вновь перемещается в точку В, и так до бесконечности, пока колебания не затихнут. Состояние маятника «в пути» можно рассматривать как дискретное состояние;
- как нечто целое, состоящее из отдельных частей. Например, дискретная структура.
Далее проанализируем особенности применения термина в различных областях.
Что такое дискретный
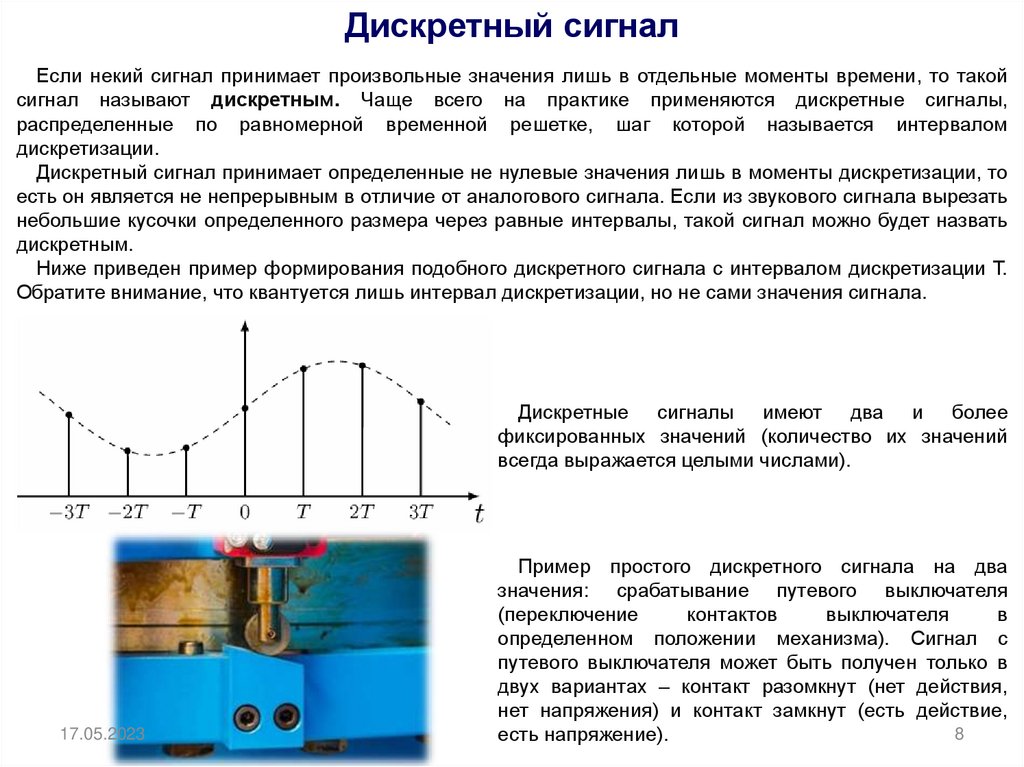
Дискретность применяется в вычислительной технике для пакетной передачи данных
Дискретный сигнал — тот, который в некотором интервале может принимать определённое число значений.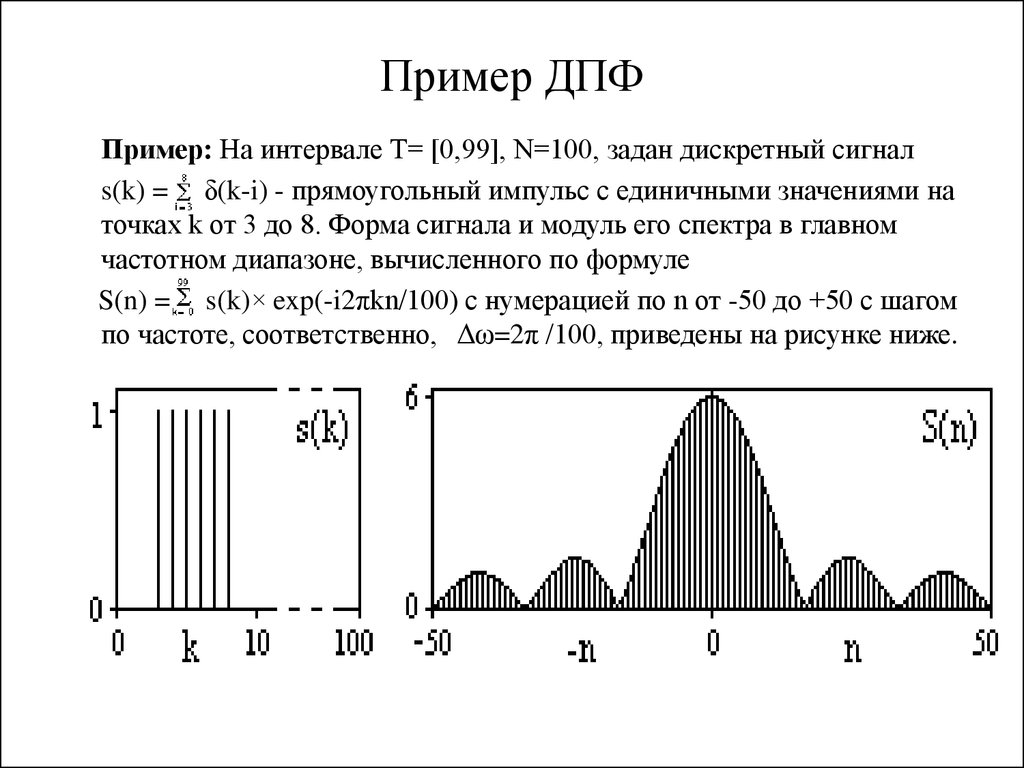 К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.
К таким сигналам относятся показания цифровых часов или приборов, а также тексты в книгах.
Благодаря достижениям в цифровой технике большинство электронных устройств в настоящее время являются цифровыми и работают с ДС. В то же время физические сигналы в природе имеют аналоговый вид. Преобразование НС в дискретный вид производится путём дискретизации его с помощью специальных устройств (АЦП). Обратное преобразование сигнала производится с помощью ЦАП.
Достоинствами цифровых систем, работающих на ДС, являются:
- высокая помехозащищённость и возможность работы каналов связи при больших шумах;
- простота передачи команд управления каналами;
- возможность цифровой обработки сигналов;
- лёгкость засекречивания.
Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, то есть внутреннее представление информации в нём дискретно.
Дискретизация входных сигналов (если она непрерывна) позволяет сделать их пригодными для дискретной обработки.
Все значения дискретного сигнала можно пронумеровать целыми числами
Основным отличием непрерывного сигнала от ДС является то, что он может иметь в заданном диапазоне любое значение, тогда как ДС может принимать только определённые значения.
К недостаткам систем, использующих ДС, можно отнести:
- увеличение полосы частот, требуемой для передачи сообщений;
- для обеспечения точного воспроизведения непрерывного сигнала при дискретизации требуется значительное количество уровней квантования и высокая частота;
- требование синхронизации;
- плохая совместимость с уже имеющимися аналоговыми системами.
Различные процессы могут быть описаны с помощью непрерывных или дискретных сигналов. Непрерывный сигнал может иметь любое значение из некоторого диапазона величин, тогда как для дискретного сигнала возможные его значения определены заранее.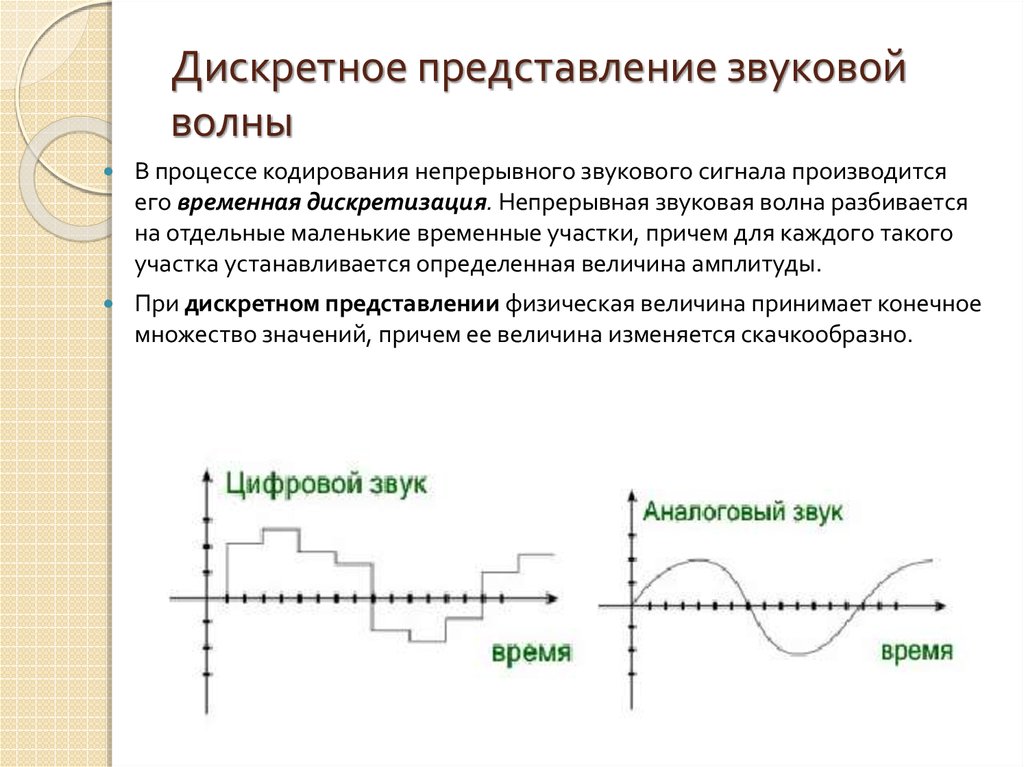 Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.
Во многих случаях при использовании цифровых методов обработки информации полезно преобразовать непрерывные сигналы в дискретные.
Существующие современные технологии связи, в том числе и разработанные для этого компьютерные программы, обеспечивают передачу голоса, являющегося звуковым потоком. При этом разработчики подобного оборудования и программного обеспечения сталкиваются с тем, что голосовой поток это непрерывная волна, передача которой возможна только на канале с высокой пропускной способностью. Его применение слишком затратно как в плане ресурсов, так и финансово. Эта проблема решается использованием принципов дискретности.
Дискретный сигнал представляет собой вместо стандартной непрерывной волны специальное цифровое выражение, способное ее описать. С установленной частотой параметры волны конвертируются в цифровую информацию и отправляются для приема. Фактически, получается обеспечить связь с минимальным применением ресурсов и энергии.
Дискретность позволяет существенно уменьшить суммарный поток данных, формируя из него пакетную передачу. При этом благодаря тому, что соблюдается выборка волны с промежутками между работой и паузами, то исключается вероятность искажения. Создается гарантия, что отправленная часть пакетных данных будет доставлена по предназначению, а за ней уже передастся следующая часть. В случае же с обыкновенными волнами, возможность помех намного выше.
При этом благодаря тому, что соблюдается выборка волны с промежутками между работой и паузами, то исключается вероятность искажения. Создается гарантия, что отправленная часть пакетных данных будет доставлена по предназначению, а за ней уже передастся следующая часть. В случае же с обыкновенными волнами, возможность помех намного выше.
Примеры простейшей дискретности
Учебники по физике для объяснения понятия дискретности при применении его к сигналу зачастую приводят аналогию с печатной книгой. Так, при ее чтении воспринимается непрерывный поток изложенной информации. При этом фактически вся изложенная в ней информация это код, состоящий из набора букв, пробелов и знаков препинания. Изначально способ общения человека – это голос, но посредством письма возможно записать звук с помощью буквенного кода. При этом, если рассматривать в плане емкости в килобайтах или мегабайтах, то объем напечатанного текста будет занимать меньше места, чем его звуковая запись.
Возвращаясь к примеру с книгой получается, что ее автор создает определенный дискретный сигнал, разбивая звуковой поток на блоки и излагая их определенным способом кодирования, то есть письменным языком. Сам читатель открывающий книгу посредством своих знаний в кодировании и мысли объединяет дискретные буквы в непрерывный информационный поток. Данный пример весьма удачно помогает упрощенным языком объяснить зачем нужна дискретность и почему она так тесно связана с сигналами, применяемыми в электронике.
Сам читатель открывающий книгу посредством своих знаний в кодировании и мысли объединяет дискретные буквы в непрерывный информационный поток. Данный пример весьма удачно помогает упрощенным языком объяснить зачем нужна дискретность и почему она так тесно связана с сигналами, применяемыми в электронике.
Простым примером визуальной дискретности можно назвать старые рисованные мультфильмы. Их кадр состоял из десятков картинок, которые шли друг за другом с небольшими паузами. Каждая последующая картинка немного изменяется, поэтому глазу человека кажется, что персонажи на экране двигаются. Именно благодаря дискретности вообще возможно формировать движущееся изображение.
Пример с рисованными мультфильмами отображает лишь часть свойства дискретности. Аналогичная технология применяется и при создании видео. Стоит вспомнить диафильмы или старые кинопленки, когда на одной длинной ленте идет множество маленьких картинок, при изменении которых создается эффект движения на экране. Хотя современные технологии и отошли от материальных носителей кадров такого плана, но по-прежнему используется принцип дискретности, хотя и видоизмененный.
Если дискретный сигнал квантуется как по времени, так и по уровню, то его называют цифровым сигналом
Сигнал считается непрерывным, если в заданных пределах он может иметь любое значение. С математической точки зрения это означает, что НС можно представить в виде непрерывной функции. Примерами такого сигнала является получаемый с микрофона сигнал о давлении на его мембрану звуковой волны или сигнал от термопары об измеряемой температуре.
Аналоговые системы для передачи информации, использующие НС, имеют следующие недостатки:
- пониженную помехозащищённость — это свойство связано с тем, что из-за непрерывности системы помеху, попавшую в сигнал, невозможно отличить от самого сигнала;
- затруднения при передаче сигналов управления;
- трудности при сопряжении с компьютером и другими цифровыми устройствами;
- трудности шифрования.
Дискретная форма представления информации тесно связана с двоичной системой счисления, ведь процессор обрабатывает всю информацию именно в ней. Как уже выяснилось, что ПК работает только с комбинациями двух значений 0 и 1, поэтому ему не понятно, что мы от него хотим, когда вводим в MS Excel формулу «=125,5/5». В этом случае, необходимо дискретная форма представления информации. Для преобразования из непрерывной системы в дискретную, необходимо разбить на участки. Например, если мы построим график движения поезда из точки А в точку Б по извилистой дороге, то у нас получается плавная линия, хотя на самом деле ее не может быть, ведь на разных участках движения скорость поезда изменяется. Дискретный процесс движения поезда будет выглядеть как точечный график, на котором точки, не соединены линиями и обозначают замеры скорости в разные отрезки участка.
Как уже выяснилось, что ПК работает только с комбинациями двух значений 0 и 1, поэтому ему не понятно, что мы от него хотим, когда вводим в MS Excel формулу «=125,5/5». В этом случае, необходимо дискретная форма представления информации. Для преобразования из непрерывной системы в дискретную, необходимо разбить на участки. Например, если мы построим график движения поезда из точки А в точку Б по извилистой дороге, то у нас получается плавная линия, хотя на самом деле ее не может быть, ведь на разных участках движения скорость поезда изменяется. Дискретный процесс движения поезда будет выглядеть как точечный график, на котором точки, не соединены линиями и обозначают замеры скорости в разные отрезки участка.
Исходя из этого можно резюмировать, что дискретизация в информатике – это преобразование непрерывного сигнала в дискретный.
После построения графика, все значения из десятичной системы счисления, нужно перевести в двоичный код. Когда это будет выполнено, процессор сможет работать с этой информацией.
Обратите внимание, что перевод в двоичную систему компьютер осуществляет самостоятельно, но после перевода непрерывного сигнала в дискретный.
Числовая информация представляется в дискретной форме с помощью алгоритмов кодирования, которые отвечают двум свойства: конечность и понятность. В зависимости от разрядности операционной системы 32 или 64 бита, будет меняться бинарный код чисел (количеством знаков в одном коде).
Свойства необходимые для дискретизации текстовой информации – это ценность, новизна, адекватность, полезность и истинность. Для преобразования текста в бинарный код используются следующие кодировки для русского алфавита КОИ-8, ISO, CP1251, Mac, CP866.
Звуковая информация обладает следующими основными свойствами:
- Частота волны звука.
- Амплитуда волны звука.
Перевод звука в дискретный сигнал заключается в замерах на определенных отрезках значений амплитуды. При этом процессе появляется понятие «квантование». Этот термин означает операцию, преобразующую громкость или амплитуду звуку в бинарный код.
Для графической информации основными свойствами в научной литературе определяют: полнота, объективность, достоверность, полезность, актуальность, адекватность. Но в общем смысле свойствами информации является палитра цветов, занимаемая площадь и поверхность. Кодирование графической информации осуществляется с учетом вида изображения (растровое, векторное, фрактальное, трехмерное).
Видеоинформации кодирует отдельно звуковую и графическую информацию.
Информационные параметры сигнала
Суть дискретизации информации в процессе обработки представлен как обмен сведениями, осуществляемый сигналами. Носителями которых являются физ.величины, представленные в пространстве и времени распределением сигналов. А информационными параметрами являются:
- Длительность импульсов.
- Амплитуда.
- Цвет изображения.
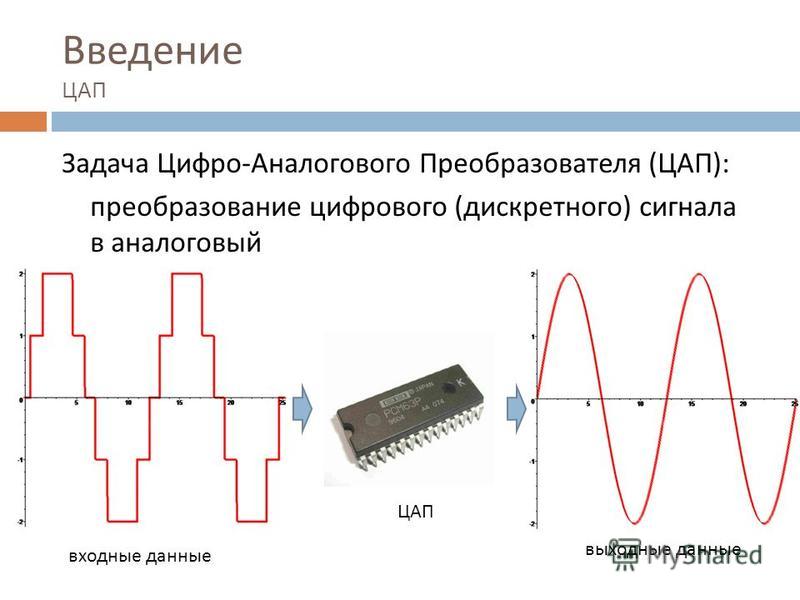
- Частота.
- Фаза сигнала.
- Продолжительность распределения импульсов в пространстве.
- Координаты точки изображения.
Этапы дискретизации
Первоначально, нужно разбить область на отрезки одинаковой длины, причем на каждом участке принимается постоянное среднее значение за показатель. Далее значения проецируют с оси х на ось у – это называется дискретным представлением функции, улучшаемую путем изменения длины отрезков в меньшую сторону.
В результате получено множество значений.
Обратите внимание, что так кодируется любое сообщение.
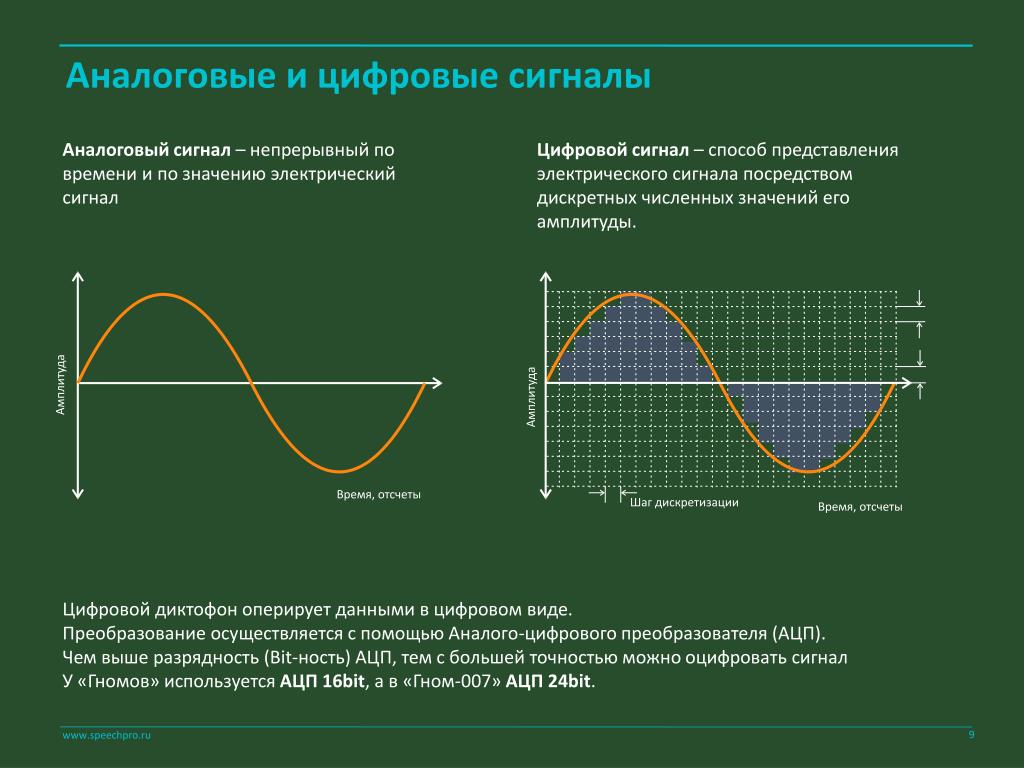
Аналоговый сигнал – это любой непрерывный сигнал, для которого изменяющаяся во времени характеристика (переменная) является представлением некоторой другой изменяющейся во времени величины. Иначе говоря, это информация, которая непрерывно изменяется во времени.
В аналоговом звуковом сигнале мгновенное напряжение непрерывно поменяется в зависимости от давления звуковых волн.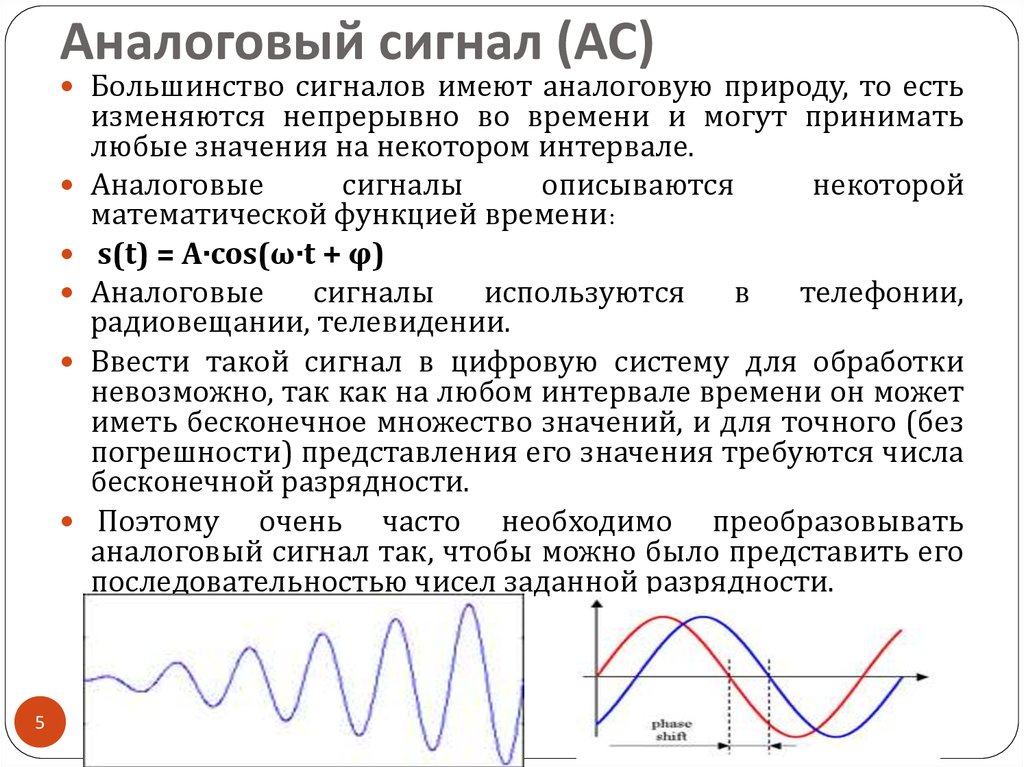 Он имеет отличия от цифрового сигнала, где перманентная величина представляет собой последовательность дискретных значений. Такая величина может принимать только одно из конечного числа значений.
Он имеет отличия от цифрового сигнала, где перманентная величина представляет собой последовательность дискретных значений. Такая величина может принимать только одно из конечного числа значений.
Термин аналоговый сигнал обычно относится к электрическим сигналам. Тем не менее, механические, гидравлические, пневматические, человеческая речь, а также иные системы могут передавать или рассматриваться как аналоговые сигналы.
Примером аналогового сигнала может служить восприятие человеческим мозгом проезжающего автомобиля. В случае, если бы его положение менялось каждые 5 секунд, аварии было бы не избежать.
Аналоговый тип сигнала непосредственно подвергается воздействию электронных шумов и искажений. Они привносятся каналами связи и операциями обработки сигналов. Они запросто могут ухудшать отношение сигнал/шум (ОСШ). Напротив, цифровые сигналы обладают конечным разрешением. Преобразование аналогового сигнала в цифровую форму вносит в сигнал низкоуровневый шум квантования. В цифровой форме сигнал может быть обработан или передан без внесения значительного дополнительного шума или искажений. В аналоговых системах трудно обнаружить, когда случается такое ухудшение. Тем не менее в цифровых системах отклонения и ухудшения могут не только обнаружиться, но и исправляться.
В цифровой форме сигнал может быть обработан или передан без внесения значительного дополнительного шума или искажений. В аналоговых системах трудно обнаружить, когда случается такое ухудшение. Тем не менее в цифровых системах отклонения и ухудшения могут не только обнаружиться, но и исправляться.
Самым серьёзным минусом аналоговых сигналов по сравнению с цифровой передачей является то, что аналоговый тип сигнала всегда содержит шум. По мере того, как сигнал передается, обрабатывается или копируется, неизбежно наличие шума, который проникает в путь прохождения сигнала. Будет происходить накопление шума как потери при генерации сигнала, постепенно и необратимо ухудшая отношение сигнал/шум. Это будет до тех пор, пока в крайних случаях сигнал не будет перегружен. Шум может проявляться как «шипение» и интермодуляционные искажения в аудиосигналах или «снег» в видеосигналах. Потери при генерации сигнала необратимы, поскольку нет надежного способа отличить шум от сигнала, отчасти потому, что усиление сигнала для восстановления ослабленных частей сигнала также усиливает шум.
Шумы аналоговых сигналов можно минимизировать благодаря экранированию, надежному подключению и использованию кабелей определенных типов, как коаксиальная или витая пара.
Любой тип информации может передаваться аналоговым сигналом. Нередко такой сигнал является измеренным откликом на изменения физических явлений, таких как звук, свет, температура, давление или положение. Физическая переменная преобразуется в аналоговый сигнал через преобразователь. К примеру, звук, который падает на диафрагму микрофона, вызывает соответствующие колебания тока. Ток генерируется катушкой в электромагнитном микрофоне. Это также может быть напряжение, которое создаётся конденсаторным микрофоном. Напряжение или ток называются «аналогом» звука.
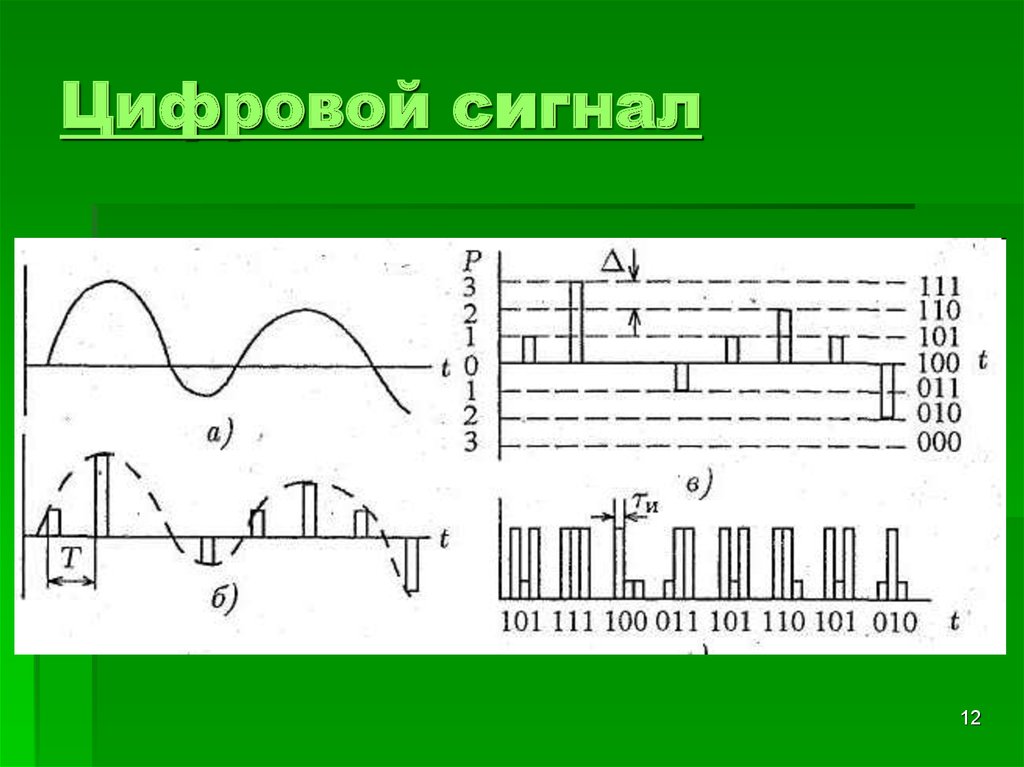
Цифровой сигнал – это сигнал, используемый для передачи данных в виде последовательности дискретных (прерывных) значений. Иначе говоря, в любой момент времени он может принимать только одно из конечного числа значений. Это и является одним из отличий от аналогового типа сигнала.
Несложные цифровые сигналы представляют информацию в дискретных полосах аналоговых уровней. Любой уровень в пределах диапазона значений имеет одно и то же информационное состояние. В большинстве цифровых цепей такой сигнал может иметь два возможных значения: двоичное и логическое. Они представлены двумя группами: одна вблизи опорного значения (обычно называется нулевыми вольтами). Другая вблизи напряжения питания.
Они соответствуют двум значениям ноль и один логического домена. Исходя из этого, в любой момент времени двоичный сигнал является одной двоичную цифру (бит). Из-за этой дискретизации относительно небольшие изменения уровней аналогового сигнала могут оставить дискретную огибающую. В результате схема игнорирует измерения состояния сигнала. Итого цифровые сигналы имеют устойчивость к помехам. Электронный шум, если он не слишком велик, не повлияет на цифровые схемы, тогда как шум всегда в значительной степени ухудшает качество аналоговых сигналов.
Иногда используются цифровые сигналы, которые обладают двумя состояниями (режимами работы).
Они имеют название двухзначная логика. Сигналы, которые же могут принимать три возможных состояния, называются трехзначной логикой.
В чем разница между аналоговым и цифровым сигналом
Аналоговый сигнал представляет собой непрерывную волну, которая постоянно меняется в течение определенного периода времени. Цифровой сигнал является также непрерывной волной, но которая несет информацию в двоичном формате и имеет дискретные значения.
Аналоговый сигнал всегда изображается в виде непрерывной синусоиды, тогда как цифровой сигнал представлен прямоугольными волнами.
Затрагивая специфику аналогового сигнала, описывается поведение волны в отношении амплитуды, периода или частоты и фазы волны. С другой стороны, затрагивая дискретные сигналы, описывается поведение волны в отношении скорости передачи битов и их интервалов.
Помимо этого, есть ещё ряд существенных отличий аналогового сигнала от цифрового:
- Диапазон аналогового сигнала строго не фиксирован.
 Диапазон цифрового сигнала конечен и может быть 0 или 1.
Диапазон цифрового сигнала конечен и может быть 0 или 1. - Аналоговый сигнал более склонен к искажениям, реагируя на шум, но цифровой – обладает устойчивостью к помехам как ответ на шум, поэтому цифровой редко сталкивается с какими-либо искажениями.
- Самым показательным примером аналогового сигнала может быть человеческий голос, а лучшим примером цифрового сигнала – передача данных в компьютер.
Аналоговое телевещание постепенно уходит в прошлое, поэтому сейчас телевизоры на 32 дюйма постепенно переходят на цифровое ТВ. Это же и касается телевизоров на 55 дюймов.
Связь и вещание цифрового типа являются практически абсолютно защищенными от шумов и от различных воздействий, которые есть у аналогового варианта. Суть в том, что используя цифровой тип, аналоговый сигнал, например, с микрофона на передающей станции автоматически преобразуется в код цифр, распространяя поток цифр и чисел. Звуку с определённой частотой и громкостью добавляется код радиоимпульсов. Частота и длительность импульсов задаётся заранее. Она одинакова как у передатчика, так и у приёмника. Импульса эквивалентен значению «1», а его отсутствие эквивалентно нулю.
Частота и длительность импульсов задаётся заранее. Она одинакова как у передатчика, так и у приёмника. Импульса эквивалентен значению «1», а его отсутствие эквивалентно нулю.
Следовательно, этот тип связи и называется цифровой. К примеру, наружная цифровая антенна для телевизора DA32 используется только для цифровых стандартов HDTV. Более того, чтобы не приобретать дорогое устройство, существует несколько способов того, как сделать антенну для цифрового ТВ своими руками.
Аналого-цифровой преобразователь – это устройство, которое задействовано в процессе преобразования аналогового сигнала в код из цифр. Аппарат, установленный в приемнике, который конвертирует код в аналоговый сигнал, – цифро-аналоговый преобразователь.
Сегодня мир постепенно отказывается от аналогового вещания, переходя на цифровое, которое является более качественным и имеет гораздо больше удобств и преимуществ.
Со времени изобретения аналоговая передача сигнала была значительно усовершенствована.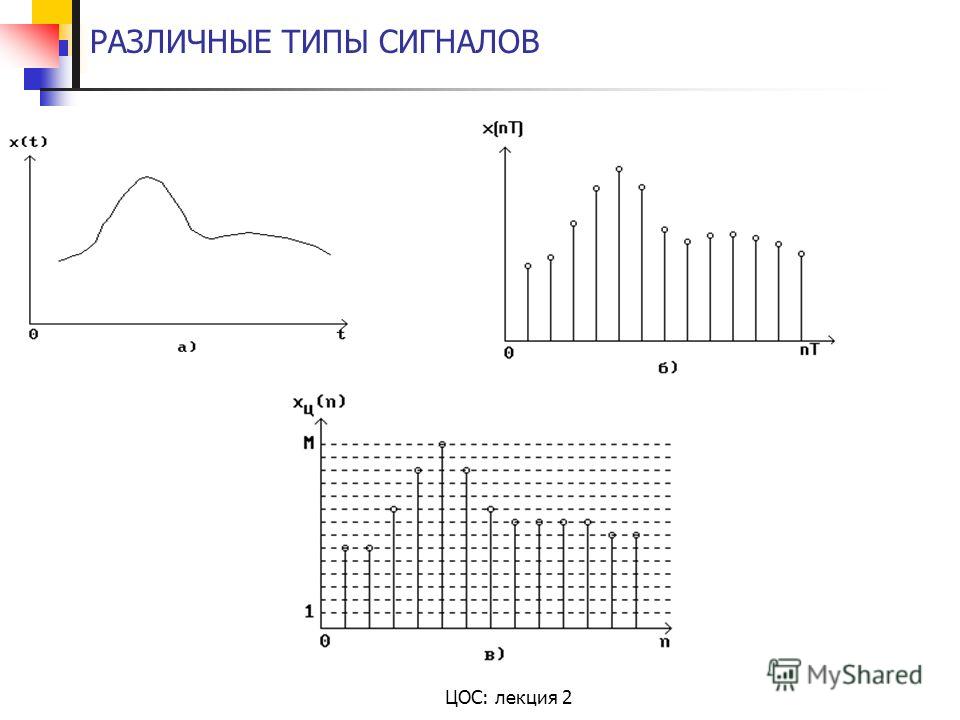 И прослужила долгое время передавая информацию, звук и изображение. Несмотря на множество улучшений сохранила все свои недостатки – шумы при воспроизведении и искажения при передаче информации. Но главным аргументом для перехода на другую систему обмена данными стал потолок качества передаваемого сигнала. Аналоговый не может вместить объём современных данных.
И прослужила долгое время передавая информацию, звук и изображение. Несмотря на множество улучшений сохранила все свои недостатки – шумы при воспроизведении и искажения при передаче информации. Но главным аргументом для перехода на другую систему обмена данными стал потолок качества передаваемого сигнала. Аналоговый не может вместить объём современных данных.
Совершенствование методов записи и хранения, прежде всего видео контента, оставили аналоговый сигнал в прошлом. Единственным преимуществом аналоговой обработки данных пока ещё является широкое распространение и дешевизна устройств. Во всём остальном аналоговый уступает цифровому сигналу.
Что такое аналоговая электроника?
Аналоговая электроника — это электроника, которая, в отличие от цифровой, работает не с дискретными сигналами, а с переменными непрерывными сигналами. Мы говорим, что цифровая электроника дискретна из-за того, что каждый сигнал может иметь только два значения. С другой стороны, в аналоговой электронике каждый сигнал имеет переменный диапазон.
Аналоговая электроника используется в аппаратном обеспечении ПК для ряда конкретных утилит, но следует особенно учитывать, что мир работает аналоговым образом и что во многих случаях необходимо преобразование цифрового сигнала в аналоговый и наоборот. .
Таким образом, наиболее очевидным примером этого являются ЦАП, цифро-аналоговые преобразователи и АЦП, аналого-цифровые преобразователи. И с этим мы также можем понять, какая из основных утилит является одной из самых популярных — утилит для динамиков и микрофонов. В первом из них цифровой сигнал преобразуется в аналоговый и через них генерируется звук. Во втором случае все наоборот, аналоговый сигнал оцифровывается.
Цифровыми сигналами гораздо проще манипулировать с помощью вычислений, не зря память хранит эти сигналы в цифровой форме, а процессоры разных типов также обрабатывают их в цифровом виде. Проблема? Цифровой требует большого количества битов и, следовательно, одновременных сигналов для достижения точности аналогового сигнала.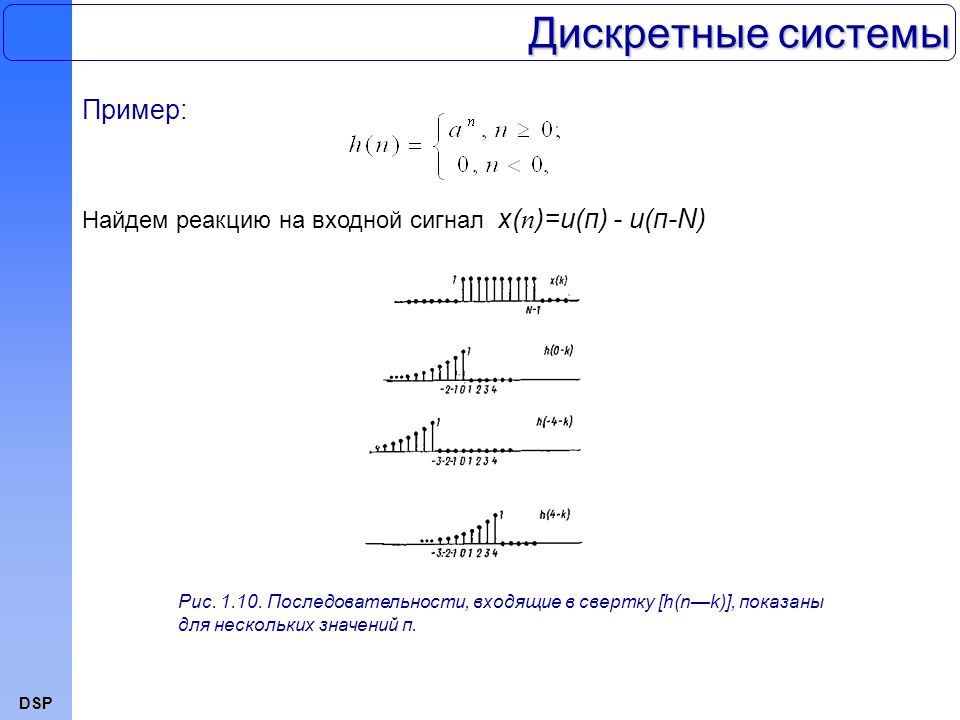
По мере того, как мы добавляем больше битов данных, мы можем сделать прямоугольную волну все более и более похожей на синусоидальную волну аналогового сигнала. Это то, что сегодня кажется нам тривиальным, но мы должны помнить, что в первые годы вычислений обработка данных была сильно ограничена из-за проблем с затратами.
В прошлом году периферийные устройства вывода, особенно мониторы, работали с аналоговыми сигналами очень низкой точности из-за процесса преобразования цифровых сигналов очень низкой точности в аналоговые. Сегодня этого больше не происходит, и мы очень точно имеем дело с изображением и звуком.
Источники
- https://KtoNaNovenkogo.ru/voprosy-i-otvety/diskretnost-diskretnyj-chto-ehto-tako.html
- https://kupi-elektriku.ru/osnovy-elektrotexniki/chem-otlichaetsya-nepreryvnyy-signal-ot-diskretnogo/
- https://electrosam.ru/glavnaja/jelektrotehnika/diskretnost/
- https://nauka.club/informatika/opisanie-protsessa-diskretizatsii-faylov-v-informatike.
 html
html - https://StroyVopros.net/elektrika/poleznaya-informatsiya/analogovyj-signal.html
- https://odinelectric.ru/knowledgebase/chem-otlichayutsya-analogoviy-signal-ot-tsyfrovogo
- https://itigic.com/ru/analog-circuits-what-they-are-made-of-and-their-utilities/
Как вам статья?
Задайте вопрос специалисту в комментариях
Нужна консультация
Дискретные сигналы — Преобразование измерительных сигналов (Инженерия)
9. Дискретные сигналы
Мы рассмотрели в предыдущих разделах методы описания аналоговых сигналов и ряд способов их преобразования: модуляцию, детектирование и фильтрацию. После осуществления модуляции сигнала, его усиления, высокочастотной фильтрации, демодуляции и низкочастотной фильтрации формируется сигнал постоянного тока, пропорциональный первичному сообщению. В таком виде сигнал может быть выведен на отчетное устройство или на самописец с целью его регистрации.
Теперь обратимся к другому классу сигналов – к дискретным сигналам и способам их преобразований.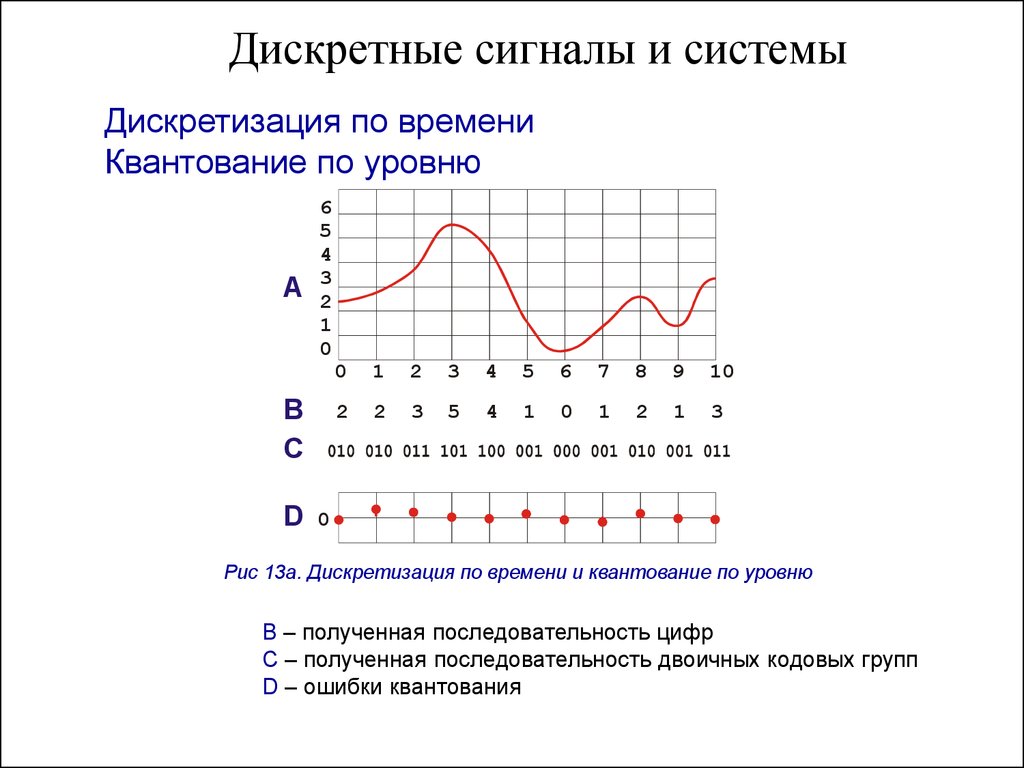 Аналоговый сигнал преобразуют в дискретный сигнал с целью его ввода в цифровой процессор. Здесь можно осуществить в цифровой форме самую изощренную обработку сигналов с целью выделения из них максимума информации, необходимой для решения поставленных перед Вами целей.
Аналоговый сигнал преобразуют в дискретный сигнал с целью его ввода в цифровой процессор. Здесь можно осуществить в цифровой форме самую изощренную обработку сигналов с целью выделения из них максимума информации, необходимой для решения поставленных перед Вами целей.
9.1 Аналого-цифровое и цифро-аналоговое преобразования
Обобщенная структура системы цифровой обработки сигналов представлена на рис. 9.1.
На вход поступает аналоговый сигнал x(t).
АЦП – аналого-цифровой преобразователь. На его выходе образуется сигнал, дискретизированный по времени и квантованный по уровню, то есть цифровой сигнал. Этот сигнал является потоком чисел, который в форме параллельного или последовательного кода поступает на цифровой процессор.
ЦП – цифровой процессор, который выполняет различные математические операции с поступающими числами. Наличие памяти позволяет запоминать и использовать в текущих расчетах ранее полученные значения сигналов. Результатом работы процессора является новая последовательность чисел.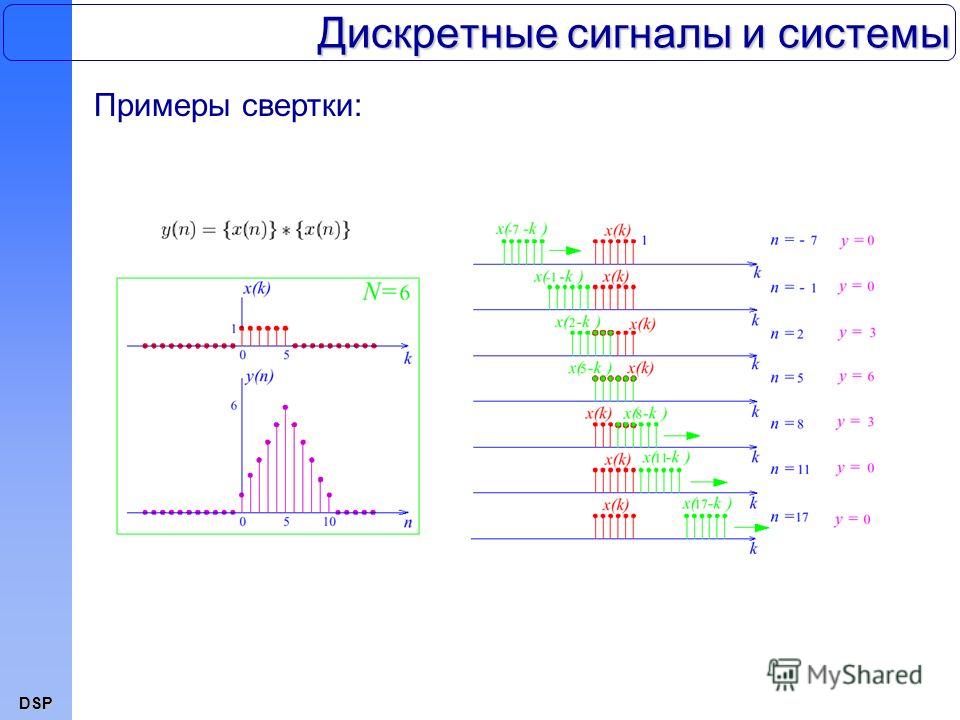 Они являются отчетами значений выходного аналогового сигнала.
Они являются отчетами значений выходного аналогового сигнала.
ЦАП – цифро-аналоговый преобразователь, осуществляющий восстановление выходного сигнала по его отчетам, образованным цифровым процессором. В результате получается ступенчатый сигнал, который еще нужно сгладить.
ФНЧ – фильтр нижних частот, осуществляющий сглаживание выходного сигнала и таким образом его преобразование в настоящий аналоговый сигнал.
В цифровой форме, то есть в цифровом процессоре, можно реализовать самые различные устройства и процедуры:
— анализаторы спектров,
— цифровые фильтры,
— нелинейные преобразования сигналов (логарифмирование, возведение в степень и т.д.), компенсация нелинейностей характеристик измерительных преобразователей,
— линейные преобразования, такие как интегрирование или дифференцирование сигналов,
— именно в цифровой форме осуществляется наиболее надежная передача данных на расстояние по каналам связи.
9.2 Дискретизация измерительных сигналов
Различные параметры физических процессов перед их вводом в любую информационную систему вначале преобразуются датчиками в электрические сигналы. В большинстве случаев эти сигналы являются непрерывно изменяющимися токами или напряжениями.
В большинстве случаев эти сигналы являются непрерывно изменяющимися токами или напряжениями.
Наиболее развитыми средствами информационной техники являются цифровые устройства, работающие с дискретными сигналами. Поэтому непрерывные сигналы необходимо уметь преобразовывать в дискретные. Это достигается тем, что непрерывные сигналы подвергаются операциям квантования по времени (дискретизации) и квантования по уровню.
В результате дискретизации реализация (рис. 9.2-а) непрерывного измерительного сигнала преобразуется в функцию дискретного времени, представленную последовательностью значений величин, называемых координатами сигнала. С помощью этих координат исходная функция непрерывного времени может быть может быть восстановлена с заданной точностью.
Координатами могут быть, например, мгновенные значения сигнала, отсчитанные в дискретные моменты времени (рис. 9.2-б).
При квантовании по уровню осуществляется преобразование величины (или координат сигнала) с непрерывной областью значений в значения величины с дискретной областью значений. Это преобразование реализуется путем замены мгновенного значения сигнала одним из конечного множества разрешенных значений или уровней квантования (рис. 9.2-в).
Это преобразование реализуется путем замены мгновенного значения сигнала одним из конечного множества разрешенных значений или уровней квантования (рис. 9.2-в).
Если провести нумерацию уровней, то значению сигнала (или его координатам) будет поставлено в соответствие некоторое число (например, – от -18 до +16 на рис. 1в), которое может быть выражено в двоичном или другом коде. Тогда каждое значение сигнала представляется последовательностью сигналов двух уровней, где наличие или отсутствие импульса на определенном месте соответствует нулю или единице в данном разряде двоичного числа. Так получается цифровая форма представления сигнала.
9.3 Общие сведения о методах дискретизации сигналов.
В самом общем виде дискретизацию реализации непрерывного сигнала на интервале времени совокупностью координат сигнала и последующее восстановление по ним исходного сигнала в виде его оценки можно записать в виде:
где — оператор представления сигнала совокупностью координат,
— оператор восстановления сигнала путем получения его оценки по совокупности координат.
Разность
образует погрешность дискретизации и восстановления сигнала.
Операторы представления и восстановления могут быть линейными или нелинейными, причем одному и тому же оператору представления можно поставить в соответствие различные операторы восстановления и наоборот. Решение задачи дискретизации заключается в совместном выборе пары операторов и , которые при известных статистических свойствах сигнала обеспечивают заданную погрешность дискретизации.
Линейные операторы в большей степени соответствуют требованиям простоты схемной реализации, поэтому в дальнейшем ограничимся только линейной дискретизацией. Линейные операторы представления и восстановления в самом общем виде должны иметь следующий вид:
Здесь — весовые функции, определяющие значимость различных координат сигнала,
— базисные или координатные функции.
Здесь необходимо отметить, что координаты сигнала получаются путем взвешенного (в соответствии с весовыми функциями) интегрирования сигнала по интервалу дискретизации . Это приводит к уменьшению влияния шумов за счет их усреднения за тот же интервал времени. Плохо, однако, то, что координаты сигнала получаются с некоторой задержкой во времени, по крайней мере, на время дискретизации. Для устранения этого недостатка используются специальные алгоритмы экстраполяции сигнала.
Это приводит к уменьшению влияния шумов за счет их усреднения за тот же интервал времени. Плохо, однако, то, что координаты сигнала получаются с некоторой задержкой во времени, по крайней мере, на время дискретизации. Для устранения этого недостатка используются специальные алгоритмы экстраполяции сигнала.
В зависимости от выбора весовых функций координаты сигнала могут представлять собой различные образования.
а) Коэффициенты некоторого ряда, аппроксимирующего изменения сигнала в каждом периоде дискретизации. Это обобщенная дискретизация. В частном случае может быть . Тогда координаты сигнала – это спектральные коэффициенты сигнала в системе базисных функций , определяющих разложение сигнала на интервалах дискретизации в обобщенный ряд Фурье. Вместо самого сигнала дальнейшим преобразованиям подвергается теперь последовательность его координат.
На рис. 9.3, сверху, изображена реализация сигнала на интервале времени Т от нуля до 0.5 с. В средней части рисунка построены две копии отрезка сигнала на малом интервале времени от 0. 2 до 0.25 с.
2 до 0.25 с.
Внизу слева дискретизированный сигнал на каждом шаге дискретизации представлен двумя координатами, двумя первыми спектральными коэффициентами разложения сигнала на шаге дискретизации в ряд по системе базисных функций Лежандра.
б) Текущие мгновенные значения сигнала, то есть выборки его значений через промежутки времени .
Весовыми функциями в этом случае являются смещенные дельта – импульсы
в моменты отсчета сигнала . Выражение
определяет при этом дискретизацию выборками.
На рис. 9.3 внизу (справа) представлен результат дискретизации сигнала выборками при шаге дискретизации с моментами отсчета . Из рисунка ясно видно различие в этих двух видах дискретизации.
в) Конечные разности, то есть приращения значений сигнала в моменты отсчета. Используются разности различных порядков:
— разности первого порядка n = I:
— разности второго порядка (n = 2), то есть разности разностей первого порядка:
— разности n-того порядка, то есть разности разностей n-1-го порядка.
В этом общем случае весовыми функциями будут линейные комбинации d — функций:
,
где — число возможных сочетаний из n по k. При дискретизации разностями 1-го порядка
.
Восстановление сигнала ведется в два этапа. На первом этапе по конечным разностям вычисляются значения последовательных выборок, а затем по выборкам находится оценка исходного сигнала.
Разностная дискретизация удобна тем, что разности лежат в меньших диапазонах, чем сам сигнал. При очень малых интервалах дискретизации разности могут не превышать шага квантования сигнала по уровню. В этом случае разности говорят только о знаке изменения сигнала и могут принимать только два значения: -1 или +1. Здесь мы получаем следующий вид дискретизации.
г) Дельта — дискретизация разностями n -того порядка.
Такого рода дискретизация обладает целым рядом очевидных преимуществ, однако здесь появляются две новых составляющих погрешности дискретизации, связанных:
— с накоплением раз допущенных ошибок;
— с возможностью появления сигналов с аномально высокой скоростью изменения.
Восстановление сигнала при любых операторах представления осуществляется обобщенным полиномом
По отношению к исходному сигналу этот полином называется аппроксимирующим. В частном случае, когда в качестве координат сигнала используются выборки, а базисные функции выбраны так, что значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, этот полином называется интерполирующим.
При выбранном операторе представления задача восстановления сигнала сводится к выбору аппроксимирующего или интерполирующего полинома. При обобщенной дискретизация восстановление обычно ведется на основе аппроксимации, а при дискретизации по выборкам или разностям — путем интерполяции.
9.4 Оценка погрешности дискретизации
Погрешность дискретизации будем характеризовать дисперсией, усредненной по интервалу дискретизации :
где — значения координат сигнала с учетом воздействия шума, вызванного, например, квантованием по уровню или другими внешними и внутренними воздействиями в устройствах преобразования и передачи сигналов. Шум подвергается дискретизации вместе с полезным сигналом, поэтому можно считать импульсным шумом .
Шум подвергается дискретизации вместе с полезным сигналом, поэтому можно считать импульсным шумом .
После возведения в квадрат в результате интегрирования получаем:
Подставим сюда . Если сигнал и шум не коррелированны, то погрешность дискретизации можно представить в виде суммы двух составляющих.
Одна из этих составляющих — собственная погрешность дискретизации по не зашумленным координатам:
Вторая составляющая вызывается действием шума и ее дисперсия составляет:
,
или, после некоторых преобразований,
Если — реализация случайного стационарного сигнала с нулевым математическим ожиданием, то первое слагаемое собственной погрешности дискретизации равно его дисперсии
а входящее в третье слагаемое математическое ожидание произведения координат и можно выразить через корреляционную функцию сигнала. Для этого преобразуем вначале математическое ожидание произведения координат к виду:
.
Но произведение двух интегралов можно представить в форме двойного интеграла. Поэтому
Поэтому
.
Операция взятия математического ожидания линейна. Поэтому знаки интегрирования и взятия математического ожидания можно поменять местами. В результате получаем:
.
Математическое ожидание, входящее во второе слагаемое собственной погрешности дискретизации, можно преобразовать аналогичным образом:
Теперь, с учётом стационарности измерительного сигнала , собственная погрешность дискретизации может быть представлена в виде:
Выражение для шумовой погрешности дискретизации значительно упрощается, если предположить, что шум является белым шумом с нулевым математическим ожиданием. Тогда, по аналогии с выражением для , имеем:
Поэтому окончательно имеем
.
Входящая в последнее выражение величина называется коэффициентом фильтрующей способности выбранной системы базисных функций по отношению к внешним помехам типа белого шума.
9.5 Оптимальная дискретизация.
Задача оптимальной дискретизации состоит в отыскивании такой системы весовых и базисных функций, которая обеспечивала бы получение минимальной собственной погрешности дискретизации при заданном числе N+1 координат сигнала, или получение минимального числа N+1 координат при заданной собственной погрешности дискретизации.
Карунен и Лоэв показали, что если — это реализация случайного стационарного сигнала с корреляционной функцией, то число координат N+1 будет минимальным, если в качестве координат используются коэффициенты обобщенного ряда Фурье (все — ортогональны и нормированы) и функции удовлетворяют интегральному уравнению Фредгольма второго рода
где
являются дисперсиями i- тых координат сигнала.
Уравнение в общем случае решить невозможно, однако оно позволяет выявить близость к оптимальной различных систем координатных функций.
Если выбранная система координатных функций удовлетворяет вышеприведенному уравнению Фредгольма, то погрешность дискретизации может быть вычислена по формуле
где — дисперсия дискретизируемого сигнала. Поскольку все зависят от времени дискретизации , то, используя полученное соотношение, можно по заданной допустимой погрешности дискретизации определить конкретное значение шага дискретизации.
Реализация метода оптимальной дискретизации очень сложна. Поэтому для практических целей желательно иметь универсальные координатные функции, применение которых возможно при не очень сложной аппаратуре, но которые в то же время обеспечивали бы близость дискретизации к оптимальной.
Поэтому для практических целей желательно иметь универсальные координатные функции, применение которых возможно при не очень сложной аппаратуре, но которые в то же время обеспечивали бы близость дискретизации к оптимальной.
9.6 Обобщенная дискретизация по полиномам Лежандра
Для дифференцируемых случайных сигналов координатными функциями, близкими к оптимальным, являются полиномы Лежандра. Полиномы Лежандра, ортогональные на интервале (-1, +1), имеют вид:
Полиномы Лежандра, ортогональные на интервале , где – шаг дискретизации, получаются заменой переменных . Тогда получим координатные функции:
Мощность этих полиномов равна . Поэтому ортонормированные полиномы имеют вид . Такими же должны быть и весовые функции .
Расчёты погрешности дискретизации по формулам, приведенным в предыдущем параграфе, существенно упрощаются, если предположить, что шаг дискретизации значительно меньше интервала корреляции исходного сигнала. В этом случае корреляционную функцию можно представить рядом Тейлора по степеням вблизи нуля и при интегрировании ограничиться несколькими первыми членами разложения.
Пример
Дискретизации подвергается случайный сигнал, имеющий спектральную плотность квазибелого шума с граничной частотой . Корреляционная функция такого сигнала имеет вид:
Представим её в виде степенного ряда:
Предположим, что все координат сигнала передаются одновременно как одна обобщенная координата с частотой или , где — шаг дискретизации.
Рассмотрим случаи использования различного числа координат сигнала.
I. используется только одна координата
На каждом шаге дискретизации определяется среднее значение сигнала, которое и используется в качестве координаты сигнала и применяется затем для его восстановления:
После восстановления сигнал представляется ступенчатой линией (рис.9.4), причём высота ступеней на каждом шаге дискретизации равна среднему значению сигнала в пределах этого шага. Вертикальными линиями отмечены границы интервалов дискретизации. Погрешность дискретизации характеризуется дисперсией
причём
Подставляя сюда корреляционную функцию в виде ряда по степеням и учитывая, что и , получим:
Погрешность дискретизации
Если задана допустимая погрешность дискретизации в долях стандартного отклонения измерительного сигнала, то, пользуясь этим выражением, можно найти допустимое значение шага дискретизации
Так если ширина спектра
то
II N+1=2, используются две координаты сигнала:
— первая координата
— вторая координата
На каждом шаге дискретизации определяются теперь эти две координаты, последовательности которых и используются затем для восстановления сигнала:
Восстановленный сигнал (рис. 9.5, сравни с рис. 9.4) на каждом шаге дискретизации представляет собой отрезок прямой линии, наиболее близкий к исходной кривой. Такая аппроксимация называется кусочно-линейной.
9.5, сравни с рис. 9.4) на каждом шаге дискретизации представляет собой отрезок прямой линии, наиболее близкий к исходной кривой. Такая аппроксимация называется кусочно-линейной.
Погрешность дискретизации составляет теперь
где дисперсия уже определена, а вычисляется как
Учитывая, что
,
получим следующее выражение для дисперсии второй координаты:
Теперь вычислим погрешность дискретизации и восстановления
При известной дисперсии собственной погрешности дискретизации шаг дискретизации теперь должен определяться как
При тех же условиях, что и в первом примере, шаг дискретизации должен теперь составлять
В условиях предыдущего примера то есть той же погрешности восстановления сигнала можно добиться при шаге дискретизации, в шесть раз большем, чем при ступенчатой аппроксимации.
III N+1=3, используя три координаты сигнала, две из которых и уже были определены. Третья координата находится как
С помощью этих трех координат сигнал на каждом шаге интегрирования приближается параболами второй степени:
Погрешность дискретизации после аналогичных вычислений принимает вид
Отсюда можно вновь найти шаг дискретизации при прочих равных условиях:
Шаг дискретизации увеличился еще почти в два раза.
Этот пример демонстрирует общее положение — увеличение числа координат приводит к увеличению допустимого шага дискретизации, но по мере роста числа координат — всё в меньшей и меньшей степени. Поэтому на практике число координат выбирают равным одному или двум и крайне редко N+1 принимается равным трем.
Дискретизация и восстановление сигнала с помощью полиномов Лежандра в большинстве случаев близка к оптимальной дискретизации, однако требует довольно сложных технических средств для своей реализации. Большее распространение в измерительных информационных системах получила дискретизация выборками, то есть представление сигнала в виде последовательности отчетов, которые берутся через определенный промежуток времени Т.
Этот интервал времени называется шагом дискретизации, а соответствующая ему частота
— круговой или, соответственно, линейной частотой дискретизации. Если частота дискретизации равна 1 кГц, то это означает, что в единицу времени, то есть в секунду, берется тысяча отчетов.
В дальнейшем мы будем более подробно заниматься именно сигналами, представленными последовательностями отчетов.
9.7 Описание сигналов, представленных выборками
9.7.1 Спектр дискретного сигнала
При шаге дискретизации и круговой частоте дискретизации , соответствующей линейной частоте , дискретный сигнал , полученный после дискретизации выборками из аналогового сигнала , определяется как , где — моменты взятия отчетов аналогового сигнала, — последовательные номера отчетов сигнала.
В результате дискретизации аналоговый сигнал преобразуется в дискретный сигнал (решетчатую функцию) , который мы будем часто обозначать просто, как . Аналогом преобразования Фурье для непрерывных сигналов является дискретное преобразование Фурье, которое определяется не как интеграл, а как сумма
Полученное выражение является комплексным, его модуль определяет спектральную плотность амплитуд или амплитудный спектр дискретного сигнала, а его аргумент – фазовый спектр сигнала.
Пример.
Задан аналоговый сигнал, представленный на рис. 9.6:
.
Сигнал является суммой экспоненциального всплеска, гармоники с амплитудой 2мВ на частоте 20 рад/с и гармоники с амплитудой 0.5мВ на частоте 150 рад/ с, которую можно рассматривать как шумовую составляющую.
Амплитудный спектр такого сигнала должен содержать:
— низкочастотную область, соответствующую экспоненциальному всплеску,
— δ – образным импульсам на частотах двух гармонических составляющих сигнала: высокий импульс на частоте 20 рад / с и более низкий импульс на частоте 150 рад / с.
Амплитудный спектр сигнала, вычисленный как модуль спектральной функции
изображен на рис. 9.7.
Характер амплитудного спектра полностью соответствует сделанным ранее предположениям. Он действительно включает в себя низкочастотную часть протяженностью от 0 до ~70 рад/ с. Кроме того, спектр содержит два δ – подобных всплеска на частотах 20 и 150 рад / с, причем последний всплеск лежит за границами низкочастотной части спектра.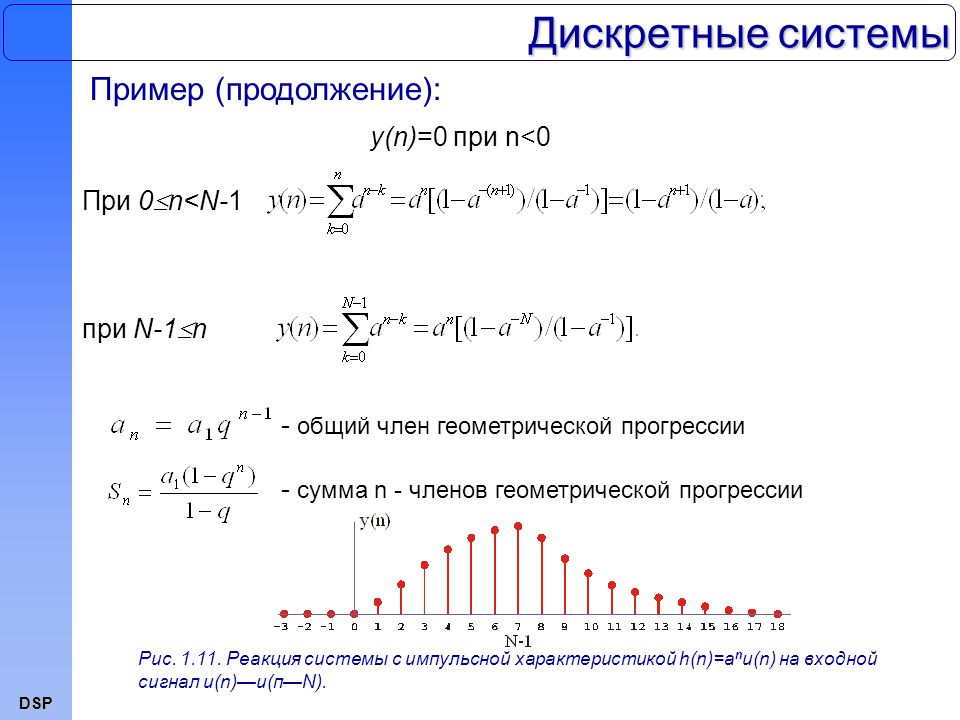
Проведем дискретизацию сигнала на частоте . Период дискретизации составит при этом Дискретизированный сигнал принимает вид:
.
Дискретный сигнал в виде последовательности отчетов в моменты времени изображен на рис. 9.8. Огибающая этого сигнала в некотором приближении повторяет исходный аналоговый сигнал (рис. 9.6), хотя некоторые его подробности могут быть и потеряны.
Дискретный сигнал должен иметь, конечно, гораздо более широкий спектр, который вычисляется по вышеприведенной формуле:
.
Спектр сигнала, вычисленный таким образом, представлен на рис. 9.9.
На рисунке четко прослеживаются основные особенности спектра дискретного сигнала и его взаимосвязь со спектром исходного аналогового сигнала. Эти особенности не связаны с конкретной формой сигнала и имеют общее значение, выходящее за рамки рассматриваемого примера.
1. Спектр дискретного сигнала периодический с периодом, равным частоте дискретизации (в нашем случае 400 рад/с).
2. В пределах половины частоты дискретизации спектр дискретного сигнала повторяет спектр исходного аналогового сигнала. Поэтому, если спектр аналогового сигнала укладывается в полосе частот, равной половине частоты дискретизации, то он без искажений повторяется с периодом, равным частоте дискретизации.
3. В этих условиях аналоговый сигнал может быть восстановлен без искажений с помощью идеального фильтра низких частот, полоса пропускания которого равна половине частоты дискретизации.
4. Если ширина спектра аналогового сигнала больше половины частоты дискретизации, то сдвинутые на период копии спектра исходного сигнала перекрывают друг друга и поэтому даже идеальный фильтр нижних частот не поможет восстановить исходный сигнал из дискретного сигнала.
На рис 9.10 представлен спектр дискретного сигнала, полученного после дискретизации того же аналогового сигнала, но при частоте дискретизации 200 рад/с, то есть вдвое меньшей, чем на рис. 9.9. Здесь пары δ – всплесков, соответствующие более высокой гармоники аналогового сигнала и находящиеся на рис.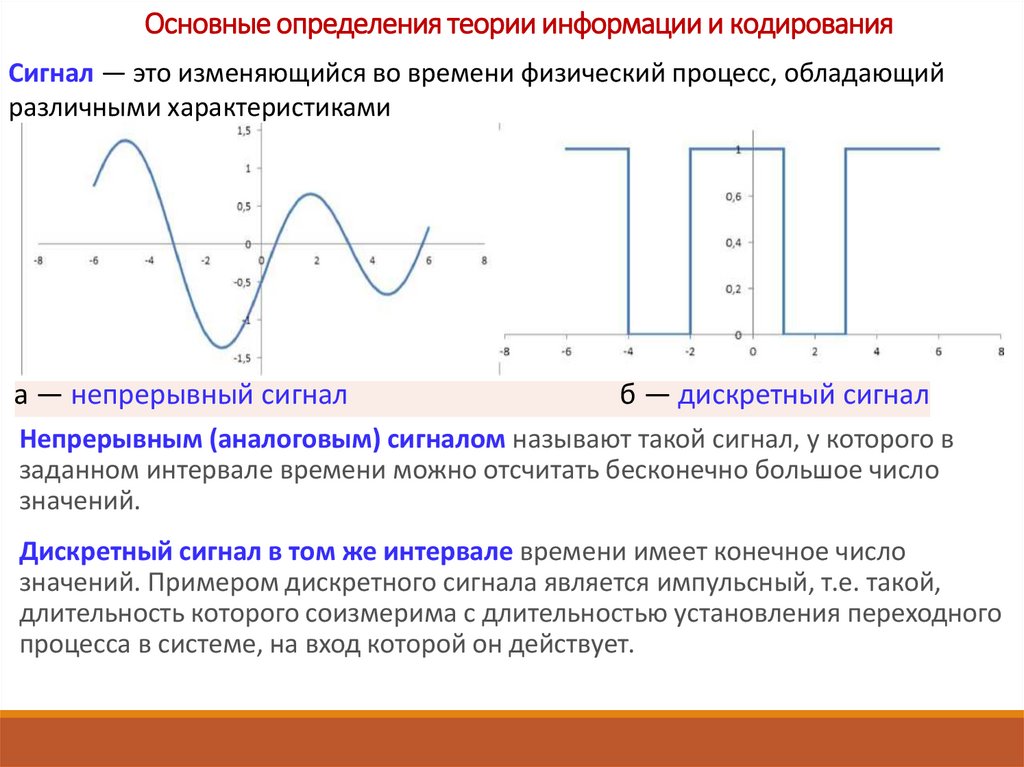 9.9 на частотах 150 рад/с и 400 – 150=250 рад/с, поменялись местами и располагаются теперь на частотах 150 рад/с и 200 – 150=50 рад/с.
9.9 на частотах 150 рад/с и 400 – 150=250 рад/с, поменялись местами и располагаются теперь на частотах 150 рад/с и 200 – 150=50 рад/с.
Восстановление аналогового сигнала с помощью идеального фильтра нижних частот с частотой среза 100 рад/с, равной половине частоты дискретизации, приведет к существенному искажению сигнала.
9.7.2 Теорема Котельникова
Возможность восстановления аналогового сигнала из последовательности его отчетов при достаточно высокой частоте дискретизации с помощью идеального фильтра нижних частот, которая была подробно рассмотрена в предыдущем разделе, формализуется теоремой Котельникова (в англоязычной литературе – теоремой Найквиста).
Теорема Котельникова звучит следующим образом. Можно со сколь угодно высокой точностью восстановить случайный аналоговый сигнал по его равномерным дискретным отчетам при соблюдении следующих условий:
— сигнал имеет ограниченный по протяженности (финитный) спектр, например от 0 до ;
— реализация сигнала наблюдается бесконечно долго как в прошлом, так и в будущем;
— дискретный сигнал формируется в виде последовательности отчетов аналогового сигнала с частотой дискретизации ;
— восстановление сигнала осуществляется по его точным (не зашумленным) отчетам с помощью обобщенного ряда Фурье по функциям отчета (функциям Котельникова):
.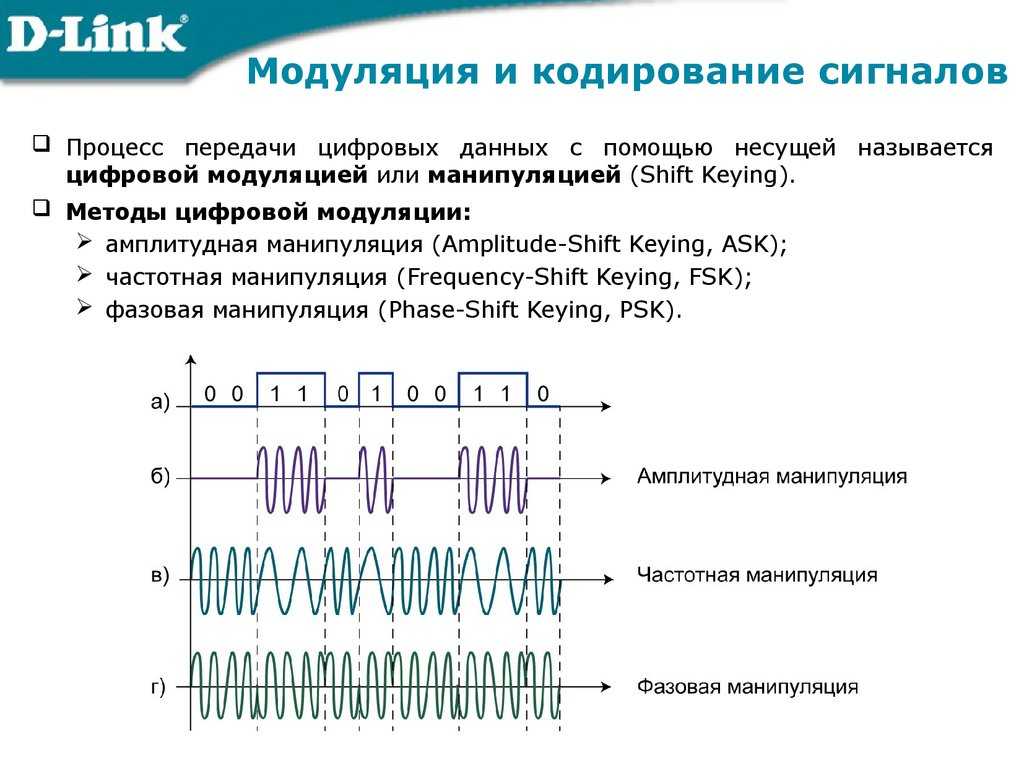
Функции отчета замечательны тем, что каждая k – тая из них принимает значение, равное единице, в момент взятия k – того отчета, и значение, равное нулю, в моменты любого другого отчета. Поэтому в моменты взятия отчетов восстановленный из дискретного сигнала аналоговый сигнал всегда совпадает с исходным аналоговым сигналом.
В качестве примера на рис. 9.11 представлена реализация некоторого аналогового сигнала x(t), а на рис. 9.12 – спектральная плотность амплитуд этой реализации. Граничная частота спектра сигнала имеет порядок 300 рад / с, поэтому частоту дискретизации сигнала можно принять равной 600 рад / с. Для простоты расчетов примем ее равной 628 рад/ с, тогда шаг дискретизации будет составлять 2π / 628=0,01 с.
На рис. 9.13 изображен небольшой фрагмент аналогового сигнала x(t) на интервале времени от 0,075 с до 0,15 с. Здесь же вертикальными отрезками представлены отчеты сигнала в моменты времени, разделенные шагами дискретизации
Ряд Котельникова представлен тремя функциями отчета (тонкие линии на рис.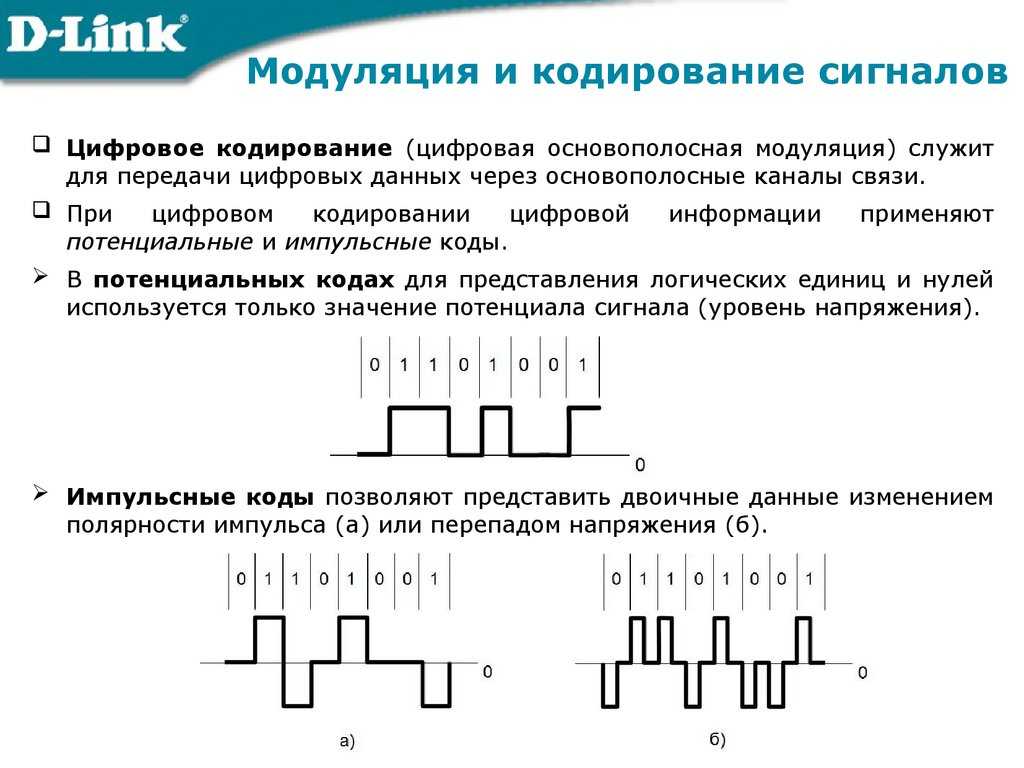 9.13), умноженными на значения отчетов, в моменты времени . Их сумма на этом интервале (0,10 – 0,12 с) уже очень близка к исходному сигналу. Степень близости восстановленного сигнала к исходному сигналу будет безгранично возрастать по мере учета все большего числа членов ряда Котельникова, если только выполняются условия ее справедливости.
9.13), умноженными на значения отчетов, в моменты времени . Их сумма на этом интервале (0,10 – 0,12 с) уже очень близка к исходному сигналу. Степень близости восстановленного сигнала к исходному сигналу будет безгранично возрастать по мере учета все большего числа членов ряда Котельникова, если только выполняются условия ее справедливости.
Следует всегда помнить, что теорема Котельникова дает лишь предельные, потенциально возможные соотношения для определения частоты дискретизации в идеализированных условиях, основными из которых является ограниченность спектра сигнала и бесконечная протяженность времени наблюдения сигнала. Однако эти соотношения практически никогда не выполняются.
Восстановление реальных аналоговых сигналов с неограниченным спектром по его отчетам, взятым за ограниченное время наблюдения, всегда связано с определенной погрешностью дискретизации, как и в случае дискретизации по полиномам Лежандра. Поэтому частоту дискретизации всегда следует выбирать гораздо большей, чем .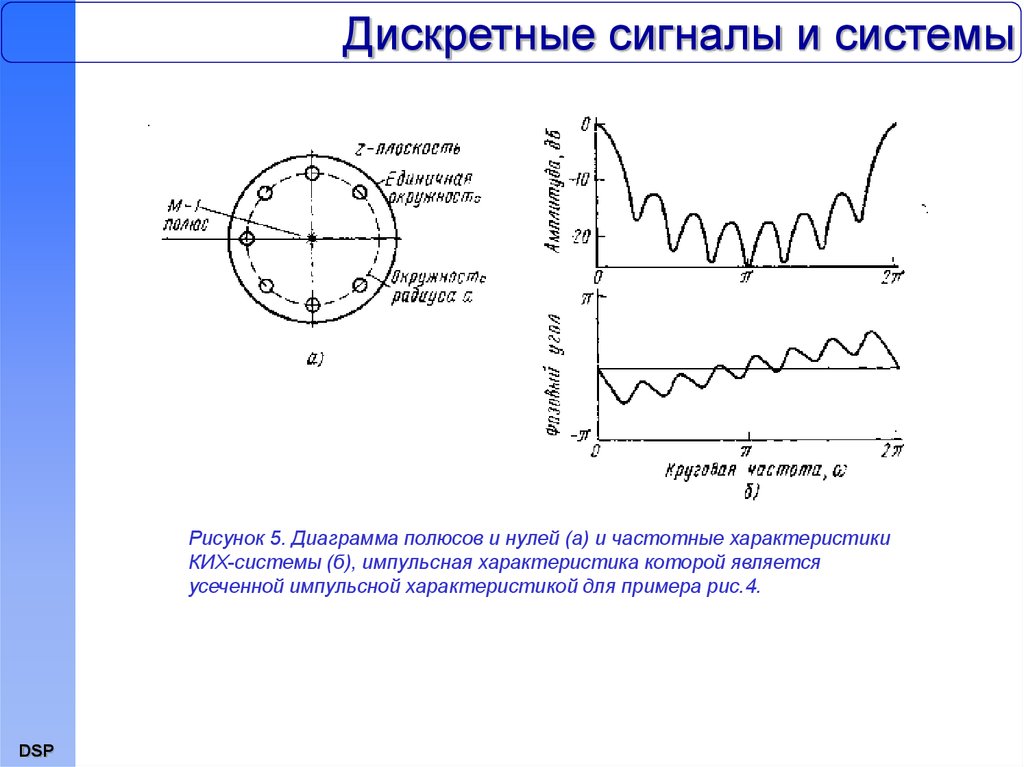 Погрешность дискретизации всегда имеет место, независимо от того, используются ли для восстановления сигнала функции Котельникова, или другие, более простые интерполяционные формулы.
Погрешность дискретизации всегда имеет место, независимо от того, используются ли для восстановления сигнала функции Котельникова, или другие, более простые интерполяционные формулы.
9.7.3 Z – преобразование дискретного сигнала
Вернемся к формуле дискретного преобразования Фурье:
.
В теории дискретных систем принято использовать несколько иную форму записи, связанную с введением Z – преобразования. Сделаем такую подстановку:
.
Тогда вышеприведенная формула значительно упростится:
.
Вновь полученная функция X(z) переменной z называется Z – изображением или Z – образом дискретного сигнала x(k).
Z – преобразования для дискретных сигналов и систем играют ту же роль, что и преобразование Лапласа для аналоговых систем. Поэтому рассмотрим ряд примеров определения Z – изображений некоторых типичных дискретных сигналов.
1. Единичный импульс (рис. 9.14) является дискретным аналогом δ — импульса и представляет собой единичный отчет с единичным значением:
Z – преобразование единичного импульса находится как
как и для δ — импульса Дирака.
2. Дискретный единичный скачок (рис. 9.15) — это полный аналог функции включения Хевисайда:
Z – образ единичного скачка найдется как
Полученная сумма – это сумма членов бесконечной геометрической прогрессии с начальным членом, равным 1, и знаменателем . Сумма членов ряда составляет:
.
3. Дискретная экспонента (рис. 9.16) — это сигнал, определяемый выражением:
При дискретная экспонента является убывающей (рис. 9.16), при — возрастающей, при — знакопеременной. Z – образ такой экспоненты
Как и в предыдущем случае, мы получили геометрическую прогрессию с нулевым членом, равным единице, но со знаменателем . Бесконечная сумма членов прогрессии определяет Z – образ экспоненты:
4. Дискретная затухающая гармоника. В противоположность предыдущим примерам запишем ее в общем виде:
где α – коэффициент затухания гармоники,
ω – частота гармоники,
φ – начальная фаза колебаний,
— период дискретизации.
Введем следующие обозначения:
На рис.9.17 представлен график дискретной затухающей гармоники при следующих данных: а=0.9, , φ=π/9. С учетом принятых обозначений выражение для дискретной затухающей гармоники можно представить в виде:
.
При получении Z – образа гармоники следует выразить функцию косинуса через сумму двух комплексных экспонент. Тогда, проделав целый ряд алгебраических и тригонометрических преобразований, в конце концов, можно будет получить следующее выражение:
.
Из приведенных примеров видно, что Z – образы большинства дискретных сигналов представляют собой дробно-рациональные функции от переменной . Происхождение Z – преобразования от преобразования Лапласа и Фурье приводит к тому, что Z – преобразование имеет и похожие свойства.
1. Линейность.
Z – преобразование линейно, так что если имеются два сигнала , то сумма этих сигналов имеет Z – образ .
2. Временная задержка дискретного сигнала.
Если дискретный сигнал x(k), имеющий Z – образ X(z), задержать на m шагов дискретизации , то задержанный сигнал y(k)=x(k-m) имеет Z – образ . Выражение можно рассматривать как оператор задержки сигнала на один шаг дискретизации.
Выражение можно рассматривать как оператор задержки сигнала на один шаг дискретизации.
3. Свертка дискретных сигналов.
По аналогии со сверткой аналоговых сигналов
,
Фурье – образ которой равен произведению Фурье – образов сворачиваемых сигналов, свертка двух дискретных сигналов определяется как
.
Z – образ свертки двух сигналов равен произведению Z – образов исходных дискретных сигналов
4. Умножение на дискретную экспоненту.
Если дискретный сигнал , имеющий Z – образ , умножается на экспоненту , то Z – образ произведения примет вид .
Рассмотренные свойства Z – преобразования позволяют во многих случаях без особого труда найти Z – образ заданного сигнала или решить обратную задачу – по известному Z – образу сигнала найти его представление во времени.
9.8 Цифровые фильтры
Под цифровым (или дискретным) фильтром понимается система преобразования дискретных сигналов, отвечающая требованиям линейности и стационарности. Линейность означает, что реакция системы на сумму сигналов равна сумме реакций на эти сигналы, подаваемые на вход системы по отдельности. Свойство стационарности системы требует того, чтобы задержка входного сигнала на произвольное число тактов (интервалов дискретизации сигнала) приводила бы только к такой же задержке выходного сигнала, никак не изменяя его форму.
Линейность означает, что реакция системы на сумму сигналов равна сумме реакций на эти сигналы, подаваемые на вход системы по отдельности. Свойство стационарности системы требует того, чтобы задержка входного сигнала на произвольное число тактов (интервалов дискретизации сигнала) приводила бы только к такой же задержке выходного сигнала, никак не изменяя его форму.
Существуют, правда, и нелинейные фильтры и фильтры с переменными параметрами, например, адаптивные фильтры, характеристики которых изменяются при изменении статистических свойств входных сигналов. Но в дальнейшем анализе мы ограничимся классом только линейных стационарных фильтров.
Понятие «фильтр » необходимо ассоциируется в нашем сознании с устройствами для подавления гармоник с частотами, лежащими в одних диапазонах, и пропускания гармоник с другими частотами. Цифровые фильтры также обладают частотно – зависимыми свойствами, однако область применения цифровых фильтров гораздо шире и охватывает вообще все виды дискретных преобразований.
Наиболее полной характеристикой фильтра является его разностное уравнение. Разностное уравнение цифрового фильтра устанавливает зависимость выходного дискретного сигнала фильтра в текущий момент времени
— от значения входного сигнала в тот же момент времени,
— от предыдущих значений входного сигнала,
— от предыдущих значений выходного сигнала.
При соблюдении требований линейности выходной сигнал фильтра должен быть линейной комбинацией предыдущих значений входного и выходного сигналов:
Здесь — коэффициенты разностного уравнения фильтра, которые полностью описывают его свойства, то есть реализуемый фильтром алгоритм преобразования входного сигнала.
Разностное уравнение фильтра можно записать в форме, очень похожей на запись линейного дифференциального уравнения стационарной аналоговой системы:
Отличие заключается лишь в том, что на месте производных входного или выходного сигналов соответствующих порядков здесь стоят сигналы, задержанные по времени на такие же числа шагов дискретизации.
Теперь подвергнем разностное уравнение фильтра Z – преобразованию:
Вынося за скобки в результаты Z – преобразования выходного и входного сигналов в обеих частях разностного уравнения, можно получить выражение для их отношения:
.
Полученное выражение носит название системной функции или функции передачи цифрового фильтра и является аналогом передаточной функции аналоговой динамической системы. Функция передачи физически реализуемой дискретной системы выражается отношением полиномов по отрицательным степеням переменной z. Функция передачи позволяет сразу же получить выражение для выходного сигнала фильтра через входной сигнал .
Для полного описания аналоговых линейных динамических систем Вы пользовались также импульсной функцией, которая представляет собой реакцию системы на входное воздействие в виде δ – импульса Дирака. Для цифровых фильтров ту же роль играет импульсная характеристика – реакция фильтра на единичный импульс. Функция передачи цифрового фильтра является результатом Z – преобразования его импульсной характеристики .
Подстановкой функция передачи цифрового фильтра превращается в его комплексный коэффициент передачи, то есть в амплитудно-фазовую частотную характеристику . Модуль комплексного коэффициента передачи образует амплитудно-частотную характеристику фильтра, а его аргумент – фазовую частотную характеристику:
Пример
Цифровой фильтр определяет среднее арифметическое из текущего и двух предыдущих значений входного сигнала. Разностное уравнение такого фильтра:
Функция передачи фильтра получается после Z – преобразования правой и левой частей этого уравнения:
и составляет:
.
Вычислим путем непосредственного подсчета импульсную функцию фильтра:
Импульсная функция равна 1/3 и остается постоянной в течении трех тактов отчета. После этого она становится равной нулю. Это означает, что импульсная функция фильтра является конечной.
Такого рода фильтры носят название КИХ-фильтры в противоположность БИХ–фильтрам, фильтрам с бесконечно – протяженной импульсной функцией.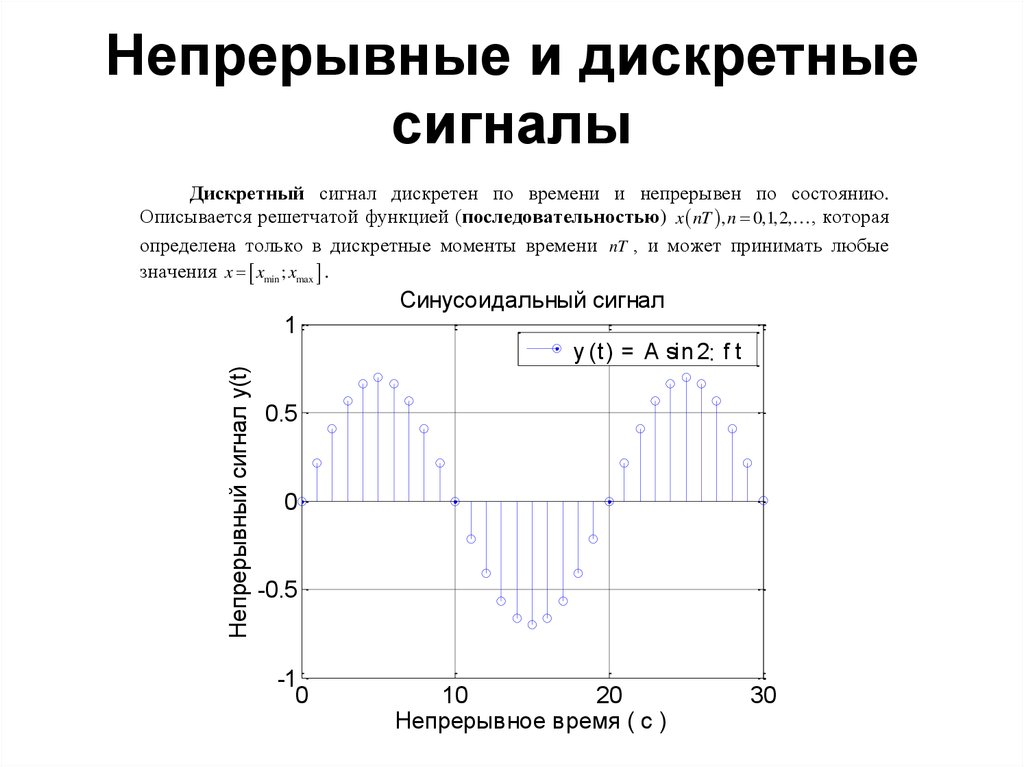
Комплексный коэффициент передачи получается из функции передачи фильтра подстановкой и составляет:
После проведения ряда тригонометрических преобразований это выражение приводится к виду:
Теперь просто определить АЧХ и ФЧХ фильтра:
Вам также может быть полезна лекция «57 Методика расследования причинения телесных повреждений».
Графики АЧХ и ФЧХ фильтра, вычисляющего значение каждого отчета как среднее арифметическое из трех предыдущих значений входного дискретного сигнала, представлены на рис.9.18. Частота дискретизации была при этом принята равной , так что интервал дискретизации равнялся 0,0157 с.
Из построенных графиков можно сделать следующие выводы относительно формы частотных характеристик цифровых фильтров:
1. Амплитудно – частотная характеристика цифрового фильтра является периодической функцией частоты, период повторения АЧХ равен частоте дискретизации.
2. Форма АЧХ цифрового фильтра определяется только выражением для функции передачи фильтра, но конкретный график АЧХ фильтра зависит от частоты дискретизации входного сигнала. Получается парадоксальный результат: свойства фильтра зависят от свойств входного сигнала. Во избежание этого парадокса частотные характеристики цифровых фильтров приходится рассматривать в функции безразмерной частоты . Именно в такой комбинации частота входит в выражение для комплексного коэффициента передачи фильтра.
Получается парадоксальный результат: свойства фильтра зависят от свойств входного сигнала. Во избежание этого парадокса частотные характеристики цифровых фильтров приходится рассматривать в функции безразмерной частоты . Именно в такой комбинации частота входит в выражение для комплексного коэффициента передачи фильтра.
3. график ФЧХ строится в виде, изображенном на графике рис. 9.18 только для того, чтобы уместить его в ограниченном пространстве рисунка. На самом деле скачков фазы на угол , конечно, нет. Запаздывание по фазе выходного сигнала относительно входного непрерывно растет линейно с ростом частоты.
4. Форма первого лепестка АЧХ полностью определяется видом функции передачи фильтра или его разностного уравнения. Подбирая соответствующим образом коэффициенты разностного уравнения фильтра можно построить фильтры нижних частот, фильтры высоких частот, полосовые и режекторные фильтры с заданными полосами прозрачности и непрозрачности.
9.1 Примеры непрерывных и дискретных сообщений.
 Дискретизация по времени и по уровню
Дискретизация по времени и по уровню Непрерывное Дискретизация
Волны дискритезазия Частоты
Непрерывное зависит от времени: звук изображение сигналы…
Дискретное: последовательность знаков
Преимущества дискретного: использование с взаимодействием цифровой среды, стандартные коды. Непрерывное сообш. Всегда можно Дискретизировать обрато можно не всегда
Дискретизация по времени U(t) U(tk) «Взятие отсчета» непрерывной величины в данный момент времени tk
(ето правило Найквиста вопрос 9.2)
Выбор шага дискретизация по времени
Выбор шага Δt (и, соответственно, частоты fd) дискретизации по времени выполняется из следующих соображений.
Очевидно, что с
уменьшением такой частоты дискретизации
пропорционально уменьшается объем
передаваемых данных, а значит — время
передачи или необходимый для хранения
объем памяти. С другой стороны, уменьшая
частоту отсчетов сигнала, мы рискуем
потерять информацию о высокочастотных
составляющих колебаний.
Частота дискретизации должна выбираться вдвое большей,
чем максимальная частота исходного сигнала:
fd = 2 fmax (3.1)
Это правило имеет простую интуитивно понятную интерпретацию: чтобы восстановить сигнал без потерь, нужно брать как минимум два отсчета на период его наиболее высокочастотной составляющей.
Дискретизация по уровню Шаг дискретизации по уровню Δu определяет максимальное значение погрешности дискретизации. При этом количество дискретных уровней сигнала очевидно можно определить исходя из диапазона его изменения:
N = (Umax — Umin)/ Δu (3.3)
С другой стороны, значение N связано с длиной чисел, которые его представляют, или, иначе говоря – с длиной цифрового кода. В общем случае такая связь устанавливается формулой:
N = mk (3.4)
Где m – основание системы счисления (или объем алфавита кода)
k – количество цифр при записи числа (длина кода).
Например, для
N=1000 необходимо три десятичных цифры (N
= 103).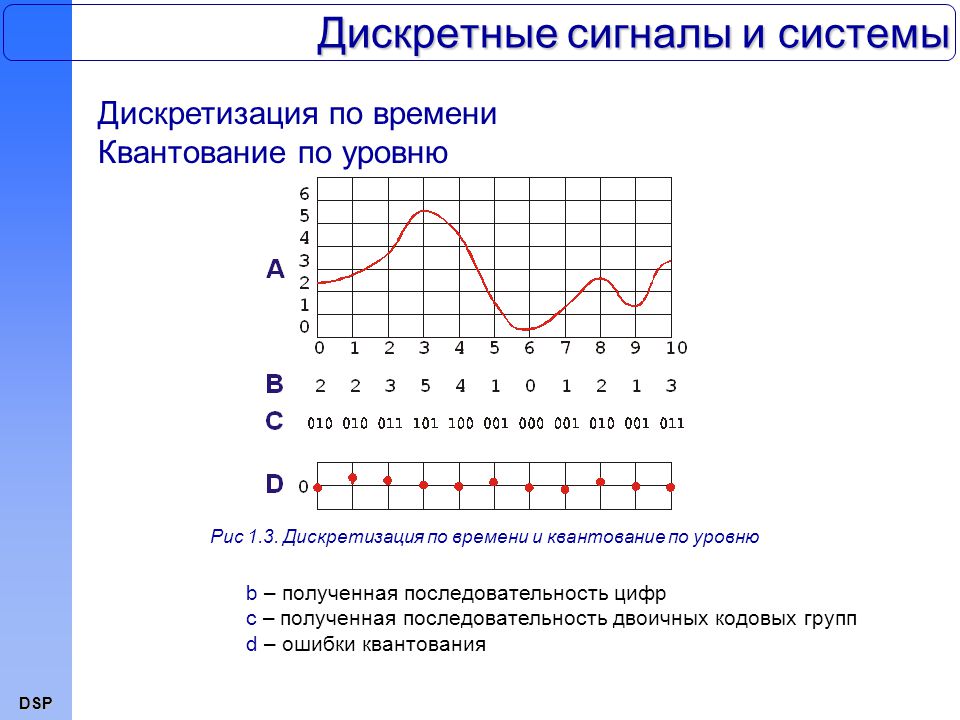 Действительно, диапазон от 000 до
999 позволяет представить 1000 чисел. Десять
двоичных разрядов позволяют закодировать
N=1024 значений (N = 210).
Действительно, диапазон от 000 до
999 позволяет представить 1000 чисел. Десять
двоичных разрядов позволяют закодировать
N=1024 значений (N = 210).
Как мы уже знаем, в современной цифровой технической среде передачи сообщений используется двоичное кодирование. Из соотношений (3.3) и (3.4) видно, что при двоичном кодировании увеличение длины кода k на один разряд позволяет увеличить количество уровней дискретизации N в два раза, а значит – вдвое сократить погрешность дискретизации Δu.
Наряду с абсолютной погрешностью Δu для характеристики точности дискретизации используется также относительная погрешность δu. Она характеризует точность дискретного представления конкретного уровня U сигнала, выраженную в % и определяется по формуле:
δu = Δu/U х 100% (3.5)
Например, если
значения сигнала кодируются восемью
двоичными разрядами (1 байт), то Δu =
Umax/28 = Umax/256 (примерно 0,4%). Такая точность
может показаться достаточно высокой,
однако, необходимо учитывать, что она
определяется по отношению к максимальному
диапазону сигнала. Вместе с тем, если
сигнал сам по себе слаб, то относительная
погрешность его дискретизации может
оказаться значительной. Так, если Uj ≈
0,1 Umax, то по при 8-разрядном кодировании
погрешность его дискретизации составит
уже около 4%. Этого, в частности,
недостаточно, чтобы с высоким качеством
воспроизводить оцифрованную музыку.
Вместе с тем, если
сигнал сам по себе слаб, то относительная
погрешность его дискретизации может
оказаться значительной. Так, если Uj ≈
0,1 Umax, то по при 8-разрядном кодировании
погрешность его дискретизации составит
уже около 4%. Этого, в частности,
недостаточно, чтобы с высоким качеством
воспроизводить оцифрованную музыку.
Для выполнения дискретизации сигнала по уровню используют широко распространенные электронные устройства (микросхемы) – аналого-цифровые преобразователи (АЦП). Функция АЦП состоит в получении двоичного кода, который соответствует амплитуде сигнала Uj, поданного на вход преобразователя. В нашем курсе нет возможности рассматривать технические детали. Отметим только, что АЦП имеют достаточное быстродействие, чтобы выполнить преобразование за время значительно меньшее Δt.
9.2 Правило Найквиста выбора частоты дискретизации. Примеры применения правила Найквиста при передаче звуковых сооющений
(см в 9.1)
9.3 Теорема Котельникова о восстановлении дискретизированной зависимости
Указанное
правило, впервые обосновал в 1928 году
Найквист. Позже оно было дополнено
строгим математическим доказательством
теоремы Котельникова, которая устанавливает
условия точного восстановления сигнала
по дискретным отсчетам. Поэтому часто
говорят о правиле и теореме
Найквиста-Котельникова.
Позже оно было дополнено
строгим математическим доказательством
теоремы Котельникова, которая устанавливает
условия точного восстановления сигнала
по дискретным отсчетам. Поэтому часто
говорят о правиле и теореме
Найквиста-Котельникова.
Теорема Котельникова гласит, что непрерывную функцию u(t), которая имеет конечный спектр с максимальной частотой fmax можно без потерь восстановить, по ее дискретным отсчетам u(kΔt), взятым с частотой fd = 1/Δt > 2 fmax,, используя процедуру: u(t) = Σ u(kΔt) sinс [2π fmax (t- kΔt)] (3.2)
Математическая функция sinс (функция Котельникова или “кардинальный синус”) определяется как sinс(x) = sinс(x)/x. Ее вид иллюстрирует рис.3.3. Согласно формуле (3.2) значения дискретных отсчетов u(kΔt) задают амплитуду каждой такой функции.
Рис.3.3. Вид функции Котельникова
Хотя согласно
теореме Котельникова fd должна быть
строго больше, чем 2 fmax , однако при этом
разница между ними может быть как угодно
мала. Таким образом, правило (3.1)
подтверждается. Однако, при доказательстве
использованы математические идеализации,
которые не вполне соответствуют
характеристикам реальных сигналов.
Так, утверждение об ограниченности
спектра означает, что сигнал должен
существовать на бесконечном интервале
времени. Суммирование в формуле ведется
также по бесконечному числу слагаемых
(k меняется от — ∞ до +∞).
Таким образом, правило (3.1)
подтверждается. Однако, при доказательстве
использованы математические идеализации,
которые не вполне соответствуют
характеристикам реальных сигналов.
Так, утверждение об ограниченности
спектра означает, что сигнал должен
существовать на бесконечном интервале
времени. Суммирование в формуле ведется
также по бесконечному числу слагаемых
(k меняется от — ∞ до +∞).
На практике частоту дискретизации с принимают согласно правилу Найквиста с некоторым запасом в сторону увеличения (обычно – порядка 10-20%).
Например, считается, что человеческое ухо не воспринимает звук с частотой выше fmax= 20 кГц. Отсюда – распространенная частота дискретизации звука fd = 44 кГц (≈20х2х1,10).
Правило выбора частоты дискретизации непрерывного сигнала широко используется на практике и его необходимо помнить.
1.5: Общие сигналы дискретного времени
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22841
- Richard Baraniuk et al.

- Университет Райса
Введение
Прежде чем приступить к изучению этого модуля, надеюсь, у вас есть представление о том, что такое сигнал и какими основными классификациями и свойствами он может обладать. В обзоре сигнал — это функция, определенная относительно независимой переменной. Эта переменная часто является временем, но может представлять любое количество вещей. Математически аналоговые сигналы с дискретным временем имеют дискретные независимые переменные и непрерывные зависимые переменные. В этом модуле описываются некоторые полезные аналоговые сигналы дискретного времени.
Важные сигналы дискретного времени
Синусоиды
Одним из наиболее важных элементарных сигналов, с которыми вам предстоит иметь дело, является синусоида с действительным знаком. В форме дискретного времени мы запишем общее выражение как
\[ A \cos (\omega n+\varphi) \nonumber \]
, где \(A\) — амплитуда, \(\omega\) — частота, а \(\varphi\) — фаза.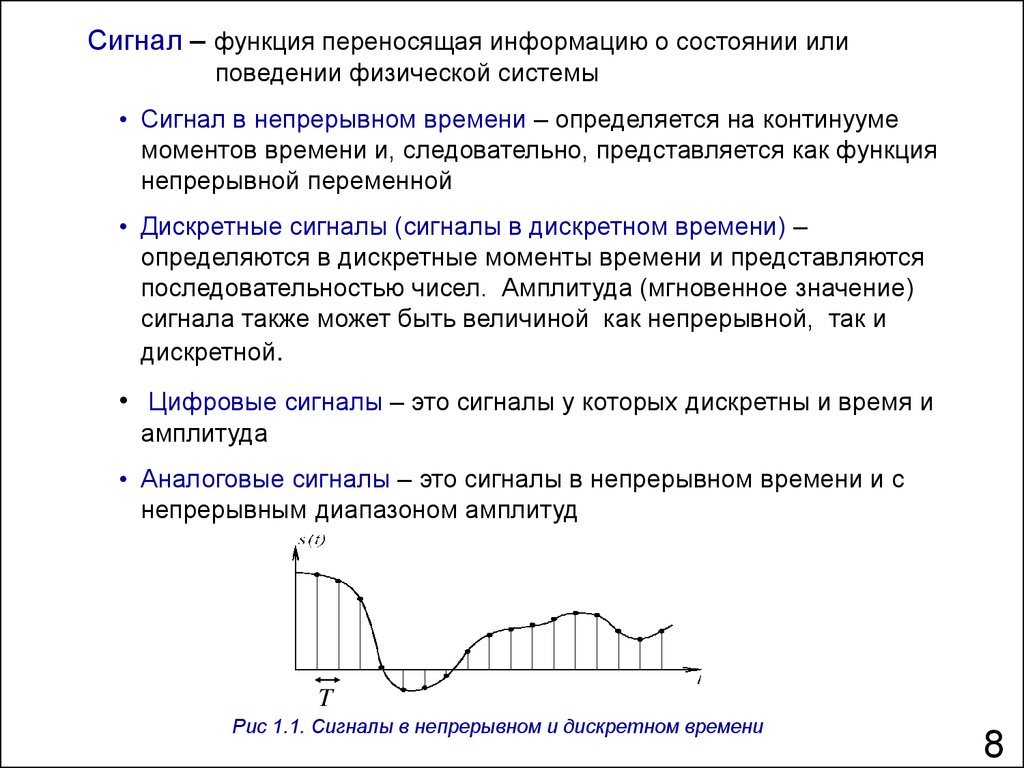 Поскольку \(n\) принимает только целые значения, результирующая функция является периодической только в том случае, если \(\frac{2 \pi}{\omega}\) является рациональным числом. 9{j(\omega+2 \pi) n} \nonumber \]
Поскольку \(n\) принимает только целые значения, результирующая функция является периодической только в том случае, если \(\frac{2 \pi}{\omega}\) является рациональным числом. 9{j(\omega+2 \pi) n} \nonumber \]
Учитывая это свойство, если у нас есть комплексная экспонента с частотой \(\omega + 2 \pi\), то этот сигнал «псевдонимирует» комплексную экспонента с частотой \(\omega\), подразумевая, что представления уравнений дискретных комплексных экспонент не уникальны.
Единичные импульсы
Вторым по значимости сигналом дискретного времени является единичная выборка , которая определяется как
\[\delta[n]=\left\{\begin{array}{l}
1 \text { если } n=0 \\
0 \text { иначе }
\end{массив}\right. \номер\]
Более подробная информация представлена в разделе, посвященном импульсной функции дискретного времени. А пока достаточно сказать, что этот сигнал имеет решающее значение при изучении дискретных сигналов, поскольку он позволяет использовать свойство просеивания при представлении и разложении сигналов.
Единичный шаг
Еще один очень простой сигнал — функция единичного шага определяется как
\[u[n]=\left\{\begin{array}{ll}
0 & \text {if } n<0 \\
1 & \text {if } n \geq 0
\конец{массив}\право. \nonumber \]
Функция шага является полезным инструментом для тестирования и определения других сигналов. Например, когда разные сдвинутые версии ступенчатой функции умножаются на другие сигналы, можно выбрать определенную часть сигнала и обнулить остальные.
Общая информация о дискретных сигналах времени
В этом модуле обсуждались некоторые из наиболее важных и наиболее часто встречающихся сигналов. Есть, конечно, и множество других сигналов, имеющих значительные последствия, которые здесь не обсуждаются. Как вы увидите позже, многие другие более сложные сигналы будут изучаться с точки зрения перечисленных здесь. Особо обратите внимание на сложные экспоненты и единичные импульсные функции, которые будут в центре внимания нескольких тем, включенных в этот курс.
Эта страница под названием 1.5: Common Discrete Time Signals распространяется по лицензии CC BY, ее автор, ремикширование и/или куратор Ричард Баранюк и др.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- Ричард Баранюк и др.
- Лицензия
- СС BY
- Программа ООР или издатель
- OpenStax CNX
- Показать оглавление
- нет
-
- Теги
-
- сложный экспоненциальный
- шт образец
- пошаговая функция
Цифровая обработка сигналов: дискретизация и дискретные сигналы
В предыдущем уроке я дал краткое представление об основах цифровой обработки сигналов. Теперь мы собираемся сделать еще один шаг в этом направлении. Чтобы выполнить часть обработки, нам сначала нужно понять сигналы дискретного времени, классификацию и их операции. В этом учебном пособии основное внимание будет уделено дискретным сигналам и системам дискретного времени .
Теперь мы собираемся сделать еще один шаг в этом направлении. Чтобы выполнить часть обработки, нам сначала нужно понять сигналы дискретного времени, классификацию и их операции. В этом учебном пособии основное внимание будет уделено дискретным сигналам и системам дискретного времени .
Что мы изучим в этом уроке: —
Ø Выборка
{ Ø Discrete-time Signals
{C}{ Ø Classification of Discrete-time signals
Ø Transformation of Discrete-time signals
Sampling
First we need to understand what is Процесс выборки ? Зачем нужна выборка ? Ответ на первый вопрос заключается в том, что сэмплирование — это процесс преобразования непрерывного сигнала в дискретный сигнал. В непрофессиональном определении вывод системы записывается через разные интервалы времени, эти интервалы времени не обязательно могут быть одинаковыми, но в этой серии руководств мы ограничим наше обсуждение только Выборка униформы .
Рис. 1. График, показывающий равномерную выборку набор значений S i (t) от i=0 до n называется выборками S(t). Интервал времени между двумя последовательными интервалами выборки называется Период выборки или Интервал выборки . Если временной интервал между двумя последовательными интервалами выборки одинаков и равен T,
f s = 1/T , , где f s — частота дискретизации.
Синусоиды с дискретным временем :-
Синусоиды с дискретным временем представляют собой очень важный тип сигнала, который следует изучать в рамках программы цифровой обработки сигналов. Итак, поскольку теперь у нас есть краткое представление о выборке, мы обсудим эти сигналы, а затем перейдем к теореме выборки. Синусоидальный сигнал с дискретным временем может быть выражен как
x(n)= Acos(? 0 n + Ø) , -? < п < +?
Где n — целое число, ? 0 — угловая частота, а также равна 2?f 0 , где f 0 — частота, а Ø — фаза сигнала. Синусоиды с дискретным временем являются периодическими, только если частота сигнала является рациональным числом. Нам нужно доказать это утверждение,
Синусоиды с дискретным временем являются периодическими, только если частота сигнала является рациональным числом. Нам нужно доказать это утверждение,
x(n+N) = x(n)
или, cos[2?f 0 (n+N) + Ø] = cos[2?f 0 (n) + Ø]
или, 2?f 0 N=2k?
или, f 0 =k/N
Кроме того, существует еще одно интересное свойство синусоид с дискретным временем. Дискретные сигналы, частоты которых разделены целым числом, кратным 2? идентичны. Пусть имеется еще один сигнал x 2 (t), который отличается от предыдущего сигнала разностью фаз 2?, тогда x 2 (t) можно записать как
x 2 (t) = Acos[(? 0 +2?)n + Ø]= Acos(? 0 n+2?n + Ø)= Acos(? 0 n + Ø)
что равно предыдущему сигналу x(t). Это можно интерпретировать так, как если бы сигнал имел частоту |?| > ?. Тогда можно сказать, что этот сигнал идентичен другому сигналу, полученному из сигнала с частотой |?| < ?.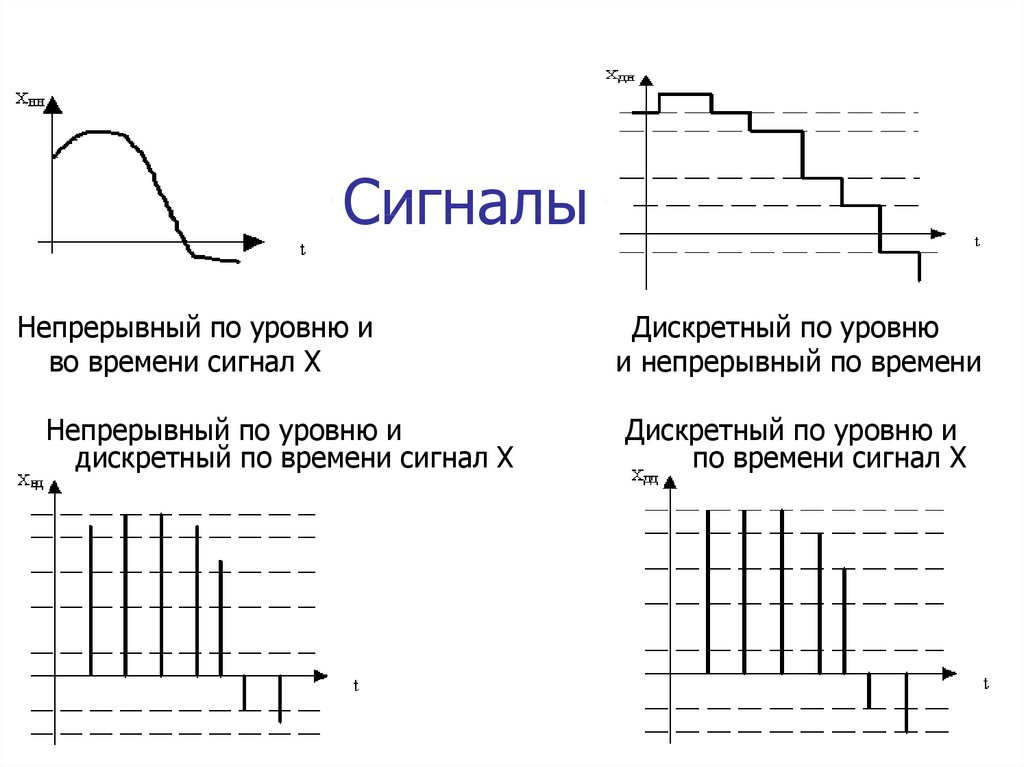 Таким образом, мы можем сказать, что
Таким образом, мы можем сказать, что
|?|? ?
Или, |f| ? ½
Все частоты в указанном выше диапазоне считаются уникальными, а все остальные частоты называются псевдонимами. Теперь пришло время ответить на второй вопрос, касающийся необходимости дискретизации: тот факт, что большинство сигналов в природе являются аналоговыми, удовлетворяет потребность в дискретизации, и, поскольку в моем предыдущем уроке я ясно показал преимущества цифровой обработки сигналов по сравнению с аналоговым сигналом. Обработка, чтобы получить дискретные сигналы, мы должны сделать выборку аналоговых сигналов. Теперь пусть х a (t) — аналоговый сигнал, а x a (t) с периодической выборкой частоты F для получения x a (nT) на частоте 1/T. Затем
Аналоговый сигнал, x a (t) = A cos(2?Ft + Ø)
Дискретный сигнал, x a (нТл) = A cos(2?FnT + Ø)
Или, x a (nT) = A cos(2?Fn/F s + Ø)
Как мы обсуждали выше в синусоидах дискретного времени |f| ? ½, Таким образом, мы заключаем, что
|F/F с | ? ½
Или, |F| ? F s /2
Таким образом, мы ясно видим, что если макс. частота сигнала равна F max , тогда частота дискретизации F s должна быть больше чем в два раза F max . Это также известно как частота дискретизации Найквиста. Всегда следует помнить, что F s должны быть в два раза больше «макс.» частотная составляющая сигнала, а не любая частота сигнала, иначе это вызовет затухание и искажение сигнала.
частота сигнала равна F max , тогда частота дискретизации F s должна быть больше чем в два раза F max . Это также известно как частота дискретизации Найквиста. Всегда следует помнить, что F s должны быть в два раза больше «макс.» частотная составляющая сигнала, а не любая частота сигнала, иначе это вызовет затухание и искажение сигнала.
Теорема о дискретизации: Если самая высокая частота, содержащаяся в любом аналоговом сигнале x a (t), равна F max =B, и дискретизация выполняется на частоте F s > 2B, то x a ( T) может быть точно извлечено из его образцов с использованием функции интерполяции,
G (T) = SIN (2? BT)/2? BT
Таким образом,
Дискретные сигналы
Дискретное время
Сигналы с дискретным временем
Функция (или последовательность) x(n) называется сигналом с дискретным временем, если независимая переменная принимает целые значения и несет некоторую информацию. Функция не определена в моменты времени между 2 образца, его не следует принимать за ноль, что является общим заблуждением среди студентов.
Функция не определена в моменты времени между 2 образца, его не следует принимать за ноль, что является общим заблуждением среди студентов.
Некоторые основные или элементарные сигналы или последовательности с дискретным временем:-
{C}{C}{C}{C}{C}{C}{C}{C}{C}{C}{ С}{С} 1. Единичная выборочная последовательность – представлена ?(n) и соответствует следующему соотношению, приведенному ниже. Этот сигнал также называют импульсом.
Рис. 2: График последовательности единичных образцов
{C}{C}{C}{C}{C}{C}{C}{C}{C}{C}{ C}{C} 2. Последовательность единичных шагов – представлена u(n) и подчиняется следующему соотношению, приведенному ниже.
Рис. 3: График последовательности шагов устройства
{ C}{C}{C}{C}{C}{C}{C}{C}{C}{C}{C}{C} 3. Сигнал рампы агрегата – представлен буквой u r (n) и следует следующему соотношению, приведенному ниже.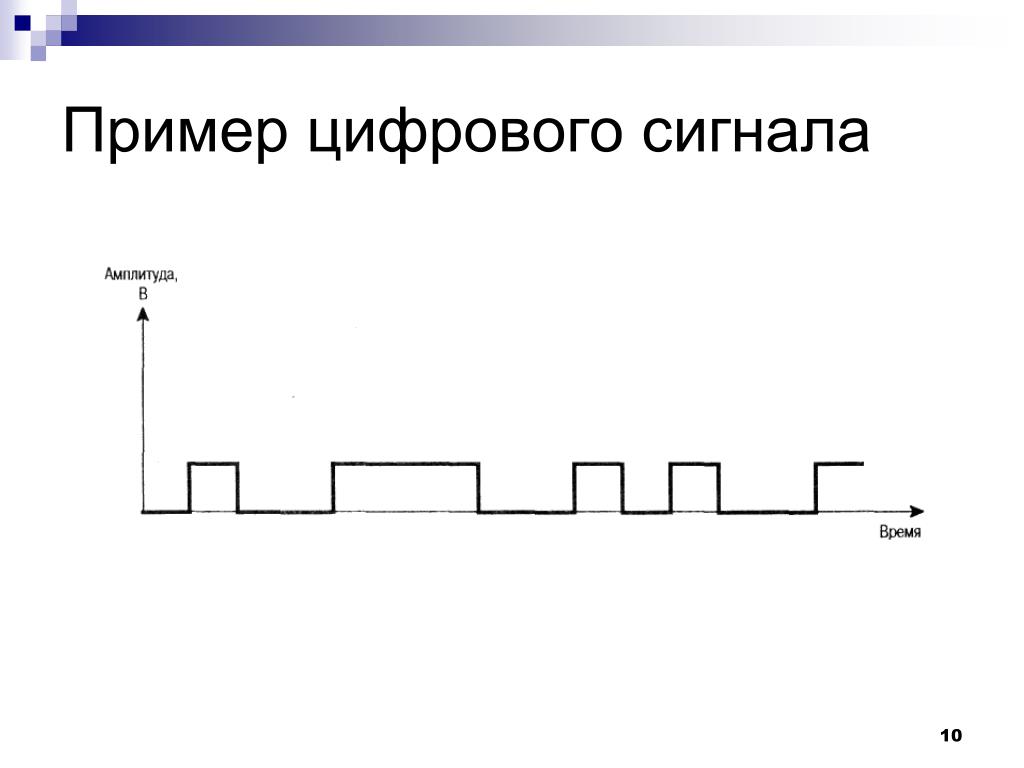
Рис. 4: График линейного сигнала агрегата
{C}{C}{C}{C}{C}{C}{C}{C}{C}{C}{ C}{C} 4. Экспоненциальный сигнал – представлен x(n) и подчиняется следующему соотношению, приведенному ниже.
x(n)= a n , для всех n
Где a — параметр, а график x(n) может быть разных типов в зависимости от значений a. Ваша задача выяснить различные возможности x(n) в зависимости от различных значений a.
Классификация дискретных сигналов
Классификация дискретных сигналов
Сигналы энергии и мощности: Пусть имеется сигнал x(n). Тогда мощность P и энергия E сигнала задаются как
Теперь, если сигнал или последовательность имеют конечную энергию, то есть E < ?. Тогда говорят, что это энергетический сигнал, и если мощность сигнала конечна, т. Е. P E < ?, то сигнал является сигналом мощности. В этом сценарии следует помнить о некоторых моментах: сигнал никогда не может быть одновременно сигналом мощности и энергии. Но сигнал не может быть ни тем, ни другим, то есть если сигнал имеет бесконечную мощность, а также бесконечную энергию. Если энергия сигнала рассчитывается за период, то она представляется как E N ,
Но сигнал не может быть ни тем, ни другим, то есть если сигнал имеет бесконечную мощность, а также бесконечную энергию. Если энергия сигнала рассчитывается за период, то она представляется как E N ,
Периодические и непериодические сигналы: Если сигнал или последовательность повторяются через фиксированный период времени, то говорят, что сигнал является периодическим по своей природе с основным периодом N, если N наименьший интервал, после которого он повторяется. В противном случае сигналы носят непериодический характер, т. е. если
Для всех n если, x(n+N)=x(n) , то x(n) является периодическим сигналом.
Симметричный (четный) и антисимметричный (нечетный) сигнал: можно сказать, что сигнал x (n) является симметричным и антисимметричным, если они следуют следующей взаимосвязи соответственно,
x (-n) = x (n) {Symmetric}
x (-n) = -x (n) {антисимметричный}
Каждый сигнал может быть выражен как комбинация четного и нечетного сигнала, где четная и нечетная составляющие получаются следующими соотношениями:
x E (n) = ½ [x (n) + x (-n)]
x o (n) = ½ [x (n)-x (-n)]
компоненты выше следуют их соответствующим условиям симметричности и антисимметричности. И теперь сигнал может быть выражен в виде суммы четных и нечетных компонентов следующим образом:0034
И теперь сигнал может быть выражен в виде суммы четных и нечетных компонентов следующим образом:0034
Преобразование независимой переменной :-
В следующих сериях руководств мы увидим, что система с дискретным временем использует некоторое преобразование исходного возбуждения в терминах независимой переменной для получения желаемого отклика. Итак, здесь мы узнаем о некотором преобразовании, которое можно выполнить с независимой переменной.
{ · Сдвиг: Сигнал x(n) можно сдвинуть во временной области, заменив n на n-k, где k — целое число, и в зависимости от знака k сигнал будет задерживаться или опережать во временной области .
x(n) => x(n-k)
Тогда, если k положительное, сигнал будет задержан во временной области, и если он начинался с n=0, то теперь он начнется с n=k -го -го интервала времени. Точно так же, если k равно –ve, сигнал будет опережать время на |k| единицы. Хотя следует учитывать, что при анализе сигналов в реальном времени опережение во времени не имеет физического значения.
Рис. 5: График, показывающий смещение сигнала
· Свертывание: Если мы заменим независимую переменную n на –n, то это называется складыванием сигнала или отражением сигнала относительно начала координат n=0.
Среди студентов распространено неправильное представление о коммутативных свойствах сдвига и свертки, но следует иметь в виду, что они не являются коммутативными по своей природе, т.е. складывание задержанного сигнала не то же самое, что задержка свернутых сигналов.
Например, пусть сигнал x(n),
первый случай: x(n) сначала складывается, а затем задерживается на k единиц. Таким образом, свертывание приведет к x(-n), а затем задержка того же свернутого сигнала приведет к x{-(n-k)} = x (-п+к).
второй случай: x(n) сначала задерживается на k единиц, а затем складывается, задержка приведет к x(n-k), а затем применение свертывания приведет к преобразованию сигнала в x(-n-k).
Итак, мы видим, что в обоих случаях полученные сигналы не совпадают.
Рис. 6: График, показывающий сворачивание сигнала
Масштабирование: Третье преобразование связано с заменой n на µn и называется масштабированием сигнала по времени. В следующем уроке мы узнаем о системы с дискретным временем, их представления и их классификация. В этой серии руководств мы сосредоточимся на системе LTI (инвариантной с линейным временем), поэтому необходимо иметь некоторое базовое представление о системах с дискретным временем, чтобы глубже погрузиться в детали систем LTI.
, поданные в соответствии с: Учебные пособия
с меткой: Обработка цифровых сигналов, дискретные временные сигналы, выборка
Страница не найдена
, не найден дольше существует. Возможно, вы сможете вернуться на домашнюю страницу сайта и посмотреть, сможете ли вы найти то, что ищете. Или вы можете попытаться найти его с помощью информации ниже.
Страницы:
- Возможности публикации
- Дом
- О
- Исследования
- Киберфизические системы
- Мультимедийные и сенсорные сети
- Умная сеть
- Динамические системы
- Цифровая криминалистика
- Безопасность физического уровня
- Безопасность мультимедиа
- Восстановление слепого изображения
- Слияние изображений
- Публикации
- Журналы
- Конференции
- Курсы
- ECE 1518: Семинар по идентификации, конфиденциальности и безопасности (киберфизическая безопасность интеллектуальной сети)
- ECE 286: Вероятность и статистика
- ECE 455: цифровая обработка сигналов
- ECE 316: Системы связи
- ECE 362: цифровая обработка сигналов
- Сигналы и системы
- Цифровая обработка сигналов в реальном времени
- Системы дискретного времени
- Кибер-физическая безопасность интеллектуальной сети
- Награды
- Ресурсы
- Контакт
- Быстрые ссылки
- Блог
Категории:
- награда
- новости
- публикация
- ресурс
- карьера
- курса
- исследование
Авторы:
- admin (57)
Ежемесячно:
- Апрель 2021
- Январь 2020
- Декабрь 2019 г.
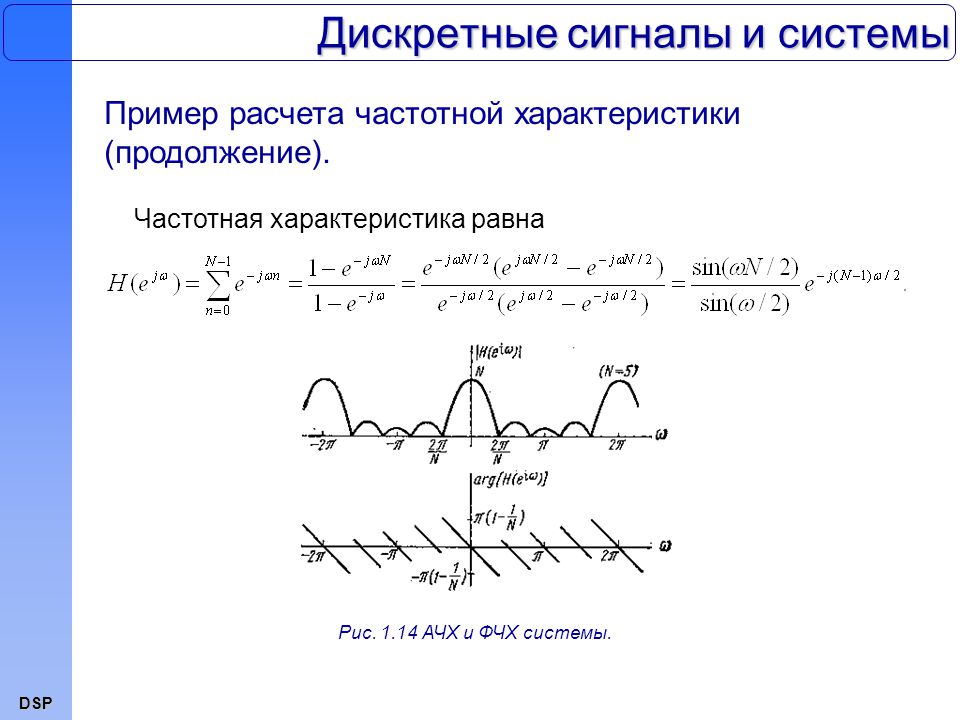
- август 2019
- Май 2019
- Январь 2019
- Апрель 2018
- Январь 2018 г.
- Декабрь 2017
- ноябрь 2017 г.
- Сентябрь 2017
- август 2017 г.
- июнь 2017 г.
- май 2017 г.
- Февраль 2017
- ноябрь 2016 г.
- Октябрь 2016 г.
- июль 2016 г.
- июнь 2016 г.
- май 2016 г.
- Март 2016 г.
- Январь 2016
- ноябрь 2015 г.
- Октябрь 2015 г.
- июль 2015 г.
- июнь 2015 г.
- Апрель 2015 г.
- март 2015 г.
- Декабрь 2014 г.
- ноябрь 2014 г.
- Октябрь 2014 г.
- май 2014 г.
- Январь 2014 г.
- ноябрь 2013 г.
- Октябрь 2013 г.
- июнь 2012 г.
- май 2012 г.
- декабрь 2011 г.
- ноябрь 2011 г.
- Апрель 2010 г.
- апрель 2009 г.
- март 2009 г.
- июнь 2004 г.
Последние сообщения:
- Текущие сообщения новостей
- CFP: Международная конференция по автономным системам 2020
- Возможности для написания дипломной работы по психиатрической информатике
- Специальный выпуск IET по интеллектуальным сетям, посвященный конфиденциальности и безопасности в интеллектуальных сетях
- Мастерская будущих дигилидеров
- Статья в журнале IEEE Signal Processing об адаптивной интеллектуальной сети
- 2019Вакансии в Исследовательской группе Кундура
- Симпозиум GlobalSIP по обработке информации, обучению и оптимизации для интеллектуальных энергетических инфраструктур
- Несколько вакансий в Исследовательской группе Кундура
- Как инженеры разрабатывают изменения
- Национальный день памяти и борьбы с насилием в отношении женщин
- Джин Кочиш получает награду Microgrid Blockchain за лучшую бумагу
- Бумага, представленная Smart Cybersecurity Network
- Elevate AI на фестивале Elevate в Торонто
- Джин Вэй получает награду НАСА за раннюю карьеру
- Пиратайини Шрикантха в выпуске, чтобы посмотреть!
- CFP: J-STSP: обработка сигналов и информации для критически важных инфраструктур
- Будут ли кибератаки усиливаться?
- Jin Wei получает награду IEEE PES GM 2016 за лучшую статью
- Зимняя школа IEEE SPS по киберфизическим системам
- Хаммад и Шриканта получают стипендию CW Bowman Graduate Scholarship
- Аспирантура: 5 W за 5 минут
- Специальный выпуск IET GTD по киберфизическим энергетическим системам: проектирование, моделирование, моделирование и управление
- Семинар IEEE GLOBECOM 2016 г.


 discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.
discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.