Как температура влияет на работу двигателя постоянного тока. Почему важно учитывать температурные эффекты при проектировании систем с двигателями. Каковы основные параметры двигателя, изменяющиеся с температурой. Как оптимизировать работу двигателя с учетом температурных изменений.
Влияние температуры на ключевые параметры двигателя постоянного тока
Температура оказывает существенное влияние на характеристики и производительность двигателей постоянного тока. При повышении температуры изменяются следующие ключевые параметры:
- Сопротивление обмоток двигателя увеличивается
- Магнитная индукция постоянных магнитов уменьшается
- Постоянная момента KT и постоянная напряжения KE уменьшаются
- Скорость холостого хода увеличивается
- Пусковой момент уменьшается
Эти изменения приводят к изменению наклона механической характеристики двигателя и его рабочих показателей. Поэтому при проектировании систем с двигателями постоянного тока крайне важно учитывать температурные эффекты.
Изменение сопротивления обмоток двигателя с температурой
Сопротивление медных обмоток двигателя увеличивается с ростом температуры согласно формуле:
R2 = R1[1 + α(T2 — T1)]
где:
- R1 — сопротивление при начальной температуре T1
- R2 — сопротивление при конечной температуре T2
- α — температурный коэффициент сопротивления меди (примерно 0.00393 1/°C)
Например, при нагреве обмоток от 25°C до 125°C их сопротивление увеличится примерно на 39%. Это приводит к увеличению потерь мощности в обмотках и снижению КПД двигателя.
Влияние температуры на магнитные свойства постоянных магнитов
С ростом температуры уменьшается остаточная магнитная индукция Br постоянных магнитов двигателя. Степень изменения зависит от типа магнитного материала:
- Для ферритовых магнитов: около -0.2% на 1°C
- Для магнитов NdFeB: от -0.09% до -0.15% на 1°C
- Для магнитов SmCo: около -0.035% на 1°C
Уменьшение магнитной индукции приводит к пропорциональному снижению постоянных момента KT и напряжения KE двигателя.
Изменение механической характеристики двигателя с температурой
Механическая характеристика двигателя постоянного тока описывает зависимость частоты вращения от момента нагрузки. При повышении температуры происходит следующее:
- Увеличивается скорость холостого хода из-за снижения KE
- Уменьшается пусковой момент из-за снижения KT и увеличения сопротивления
- Увеличивается наклон характеристики
В результате при той же нагрузке частота вращения нагретого двигателя будет ниже, чем у холодного. Это необходимо учитывать при выборе двигателя для конкретного применения.
Оптимизация работы двигателя с учетом температурных эффектов
Для обеспечения стабильной работы двигателя постоянного тока в условиях изменяющейся температуры можно применять следующие методы:
- Выбор двигателя с запасом по мощности и моменту
- Обеспечение эффективного охлаждения двигателя
- Применение систем управления с обратной связью по скорости
- Использование температурной компенсации в алгоритмах управления
- Выбор магнитных материалов с меньшей температурной зависимостью
Правильный учет температурных эффектов позволяет оптимизировать работу двигателя и обеспечить требуемые характеристики во всем диапазоне рабочих температур.
Влияние температуры на КПД двигателя постоянного тока
Повышение температуры оказывает негативное влияние на КПД двигателя постоянного тока по нескольким причинам:
- Увеличиваются потери в меди из-за роста сопротивления обмоток
- Снижается магнитная индукция, что уменьшает развиваемый момент
- Возрастают механические потери из-за изменения вязкости смазки
В результате максимальный КПД двигателя смещается в область меньших нагрузок. При работе с постоянной нагрузкой КПД нагретого двигателя будет ниже, чем у холодного.
Методы измерения температуры обмоток двигателя
Для контроля температуры обмоток двигателя в процессе работы применяются следующие методы:
- Встроенные термодатчики (термисторы, термопары)
- Измерение сопротивления обмоток
- Бесконтактное измерение ИК-излучением
- Тепловизионный контроль
Наиболее точным является метод измерения сопротивления, но он требует остановки двигателя. Встроенные датчики позволяют контролировать температуру в реальном времени.
Влияние температуры на срок службы двигателя
Повышенная рабочая температура значительно сокращает срок службы двигателя постоянного тока по следующим причинам:
- Ускоряется старение изоляции обмоток
- Снижаются свойства смазочных материалов
- Возможно размагничивание постоянных магнитов
- Увеличивается износ щеточно-коллекторного узла
Как правило, повышение рабочей температуры на каждые 10°C сокращает срок службы изоляции обмоток в 2 раза. Поэтому важно обеспечить эффективное охлаждение двигателя для увеличения его долговечности.
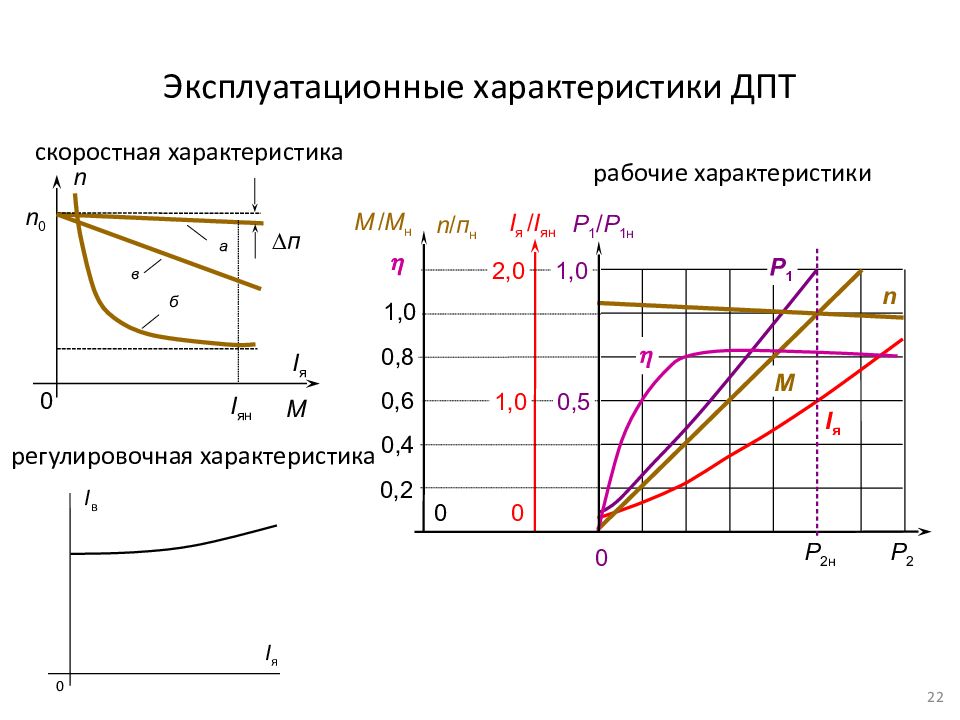
Рабочие характеристики
Рабочие характеристики ДПТ параллельного возбуждения малой мощности приведены на рис. 5.8.
Рис. 5.8
Рабочие характеристики двигателя представляют собой зависимости скорости вращения n, потребляемого тока I и мощности P1, момента на валу двигателя M, коэффициента полезного действия η от полезной мощности P2 при неизменном значении напряжения питания Uн = const, тока обмотки возбуждения Iвн=const и отсутствии добавочного сопротивления в якорной цепи Rд я
= 0. Они дают возможность судить об эксплуатационных свойствах двигателей и определять наиболее экономичные их режимы работы в условиях производства.Механическая характеристика двигателя постоянного тока
Механическими
характеристиками двигателя называются
зависимости установившейся частоты
вращения от момента на валу двигателя
– n=f1(M)
или ω=f2(M).
Характеристики называют естественными, если они получены при номинальных условиях питания (при номинальном напряжении), номинальном возбуждении и отсутствии добавочных сопротивлений в цепи якоря.
Характеристики двигателя называются искусственными при изменении любого из перечисленных выше факторов.
Подставим в уравнение ,выражения для определения тока и ЭДС ДПТ
Ея = СЕnФ,
Механическая характеристика двигателя постоянного тока с независимым и параллельным возбуждением имеет вид:
,
где Rяц = Rя + Rдоб – полное сопротивление цепи якоря, Ом;
RЯ – сопротивление обмотки якоря, Ом;
Rдоб – добавочное сопротивление в цепи якоря, Ом.
Анализируя выражение для построения механической характеристики, видим, что математически это уравнения прямой линии, пересекающей ось скоростей в точке n0, где
n0 = U/(·Ф)
– скорость холостого хода.
где Pн – номинальная мощность двигателя, Вт;
ωн – номинальная частота вращения, рад/сек.
Естественная механическая характеристика показана на рис. 5.9.
Для построения естественной механической характеристики (ЕМХ) необходимо найти две точки.
Одна из них определяется из паспортных данных двигателя для номинальных значений nн и Мн:
Мн = Pн/ωн , ωн = π·nн/30 = 0,105·nн,
где Pн – номинальная мощность двигателя, Вт;
ωн – номинальная частота вращения, рад/сек .
Вторая точка соответствует идеальному холостому ходу, когда I = 0 и М=0.
Скорость холостого хода можно найти из следующего уравнения при подстановке паспортных данных двигателя:
.
Регулирование скорости вращения дпт
Существует три основных способа регулирования частоты вращения машин постоянного тока: реостатное регулирование, регулирование изменением магнитного потока, регулирование изменением напряжения сети.
Реостатное регулирование частоты вращения осуществляется путем введения в цепь якоря дополнительных активных сопротивлений – резисторов, т.е. Rяц = (Rя + Rдоб) = var при U = Uн, Ф = Фн. Как видно из уравнения механической характеристики
при изменении величины добавочного сопротивления Rдоб в цепи якоря скорость идеального холостого хода n0 остается постоянной изменяется лишь жесткость характеристики.
Искусственные
механические характеристики (ИМХ) при
введении добавочного сопротивления в
цепь ротора двигателя постоянного тока
независимого возбуждения показаны на
рис.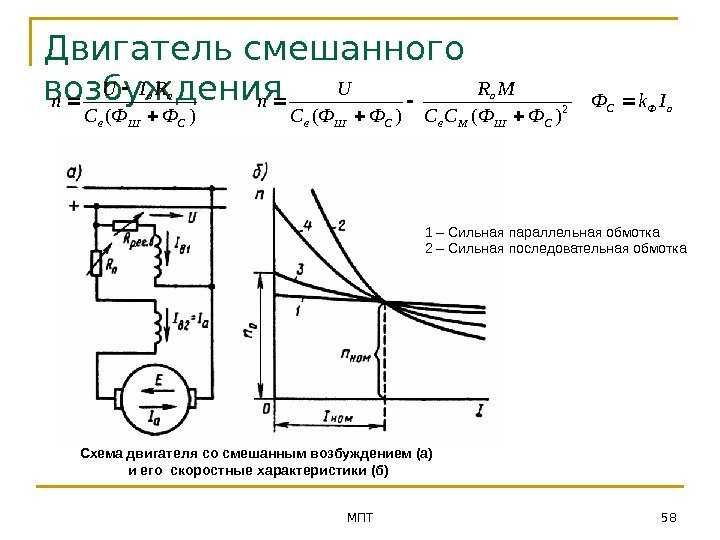
5.10.
Регулирование частоты вращения при изменении магнитного потока осуществляется преимущественно за счет ослабления магнитного потока Ф возбуждения двигателя, т.е. за счет уменьшения тока возбуждения iв.
При уменьшении магнитного потока обычно соблюдаются условия: U = Uн; Rдя= 0. В этом случае для скорости идеального холостого хода имеем
, тогда ,
где — скорость холостого хода для искусственной механической характеристики;
— скорость холостого хода для естественной механической характеристики.
Искусственные механические характеристики при уменьшении магнитного потока представлены на рис. 5.11.
Для регулирования частоты вращения двигателя постоянного токанезависимого возбуждения изменением питающего напряжения необходимы регулируемые источники напряжения.
Из
уравнения механической характеристики
видно, что с регулированием напряжения
связано изменение скорости идеального
холостого хода n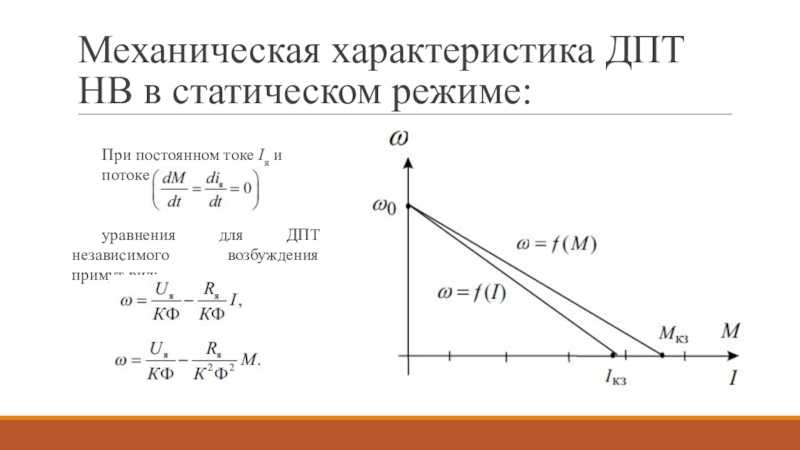
Это позволяет существенно расширить
диапазон регулирования. Регулирование
частоты вращения идет, как правило, вниз
от основной характеристики.Искусственные
характеристики при изменении
(уменьшении) напряжения будут иметь вид прямых. Механические
характеристики двигателя постоянного
тока независимого возбуждения при
изменении напряжения питания показаны
на рис. 5. 12.
20
Рабочие характеристики двигателей постоянного тока
Рабочие характеристики двигателей постоянного тока предназначены для определения характера прохождения энергии в электромеханическом преобразователе.
К рабочим характеристикам относятся характеристики: ω(P2), Iа(P2), P1(P2), M(P2), η(P2).
P2 – полезная мощность.
P1 – подводимая мощность.
Зависимость M(P2) называется моментной характеристикой.
Чтобы было более наглядно видно прохождение энергии через двигатель постоянного тока, постоим энергетическую диаграмму.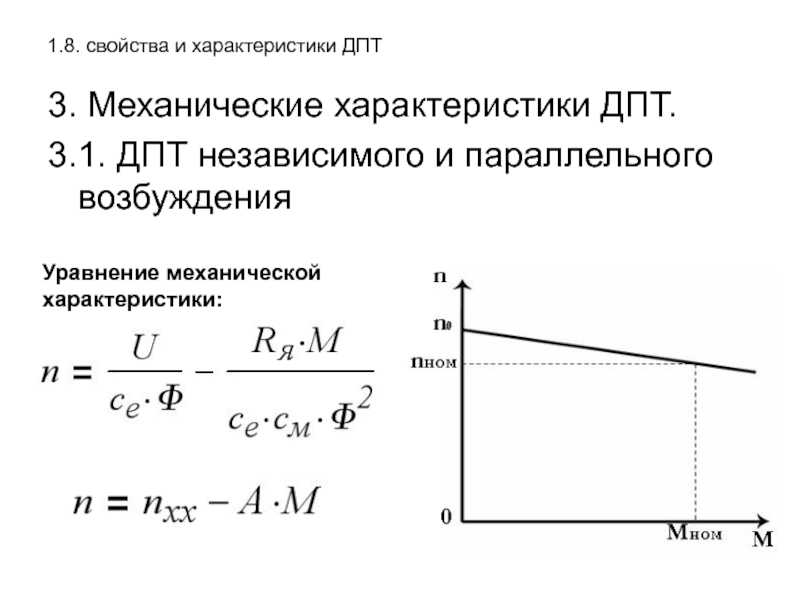
Энергетическая диаграмма строится в масштабе.
Как только по обмотке якоря начинает протекать ток, в обмотке якоря возникают электрические потери.
P1 = U · Iа
Pэл = Iа2 · rа
Полезная мощность P1 через воздушный зазор передается на вал двигателя и называется электромеханической мощностью.
Электромеханическая мощность может быть как электрическая, так и механическая, но эта мощность будет еще не полезная мощность. Часть электромеханической мощности преобразуется в магнитные потери, механически потери и добавочные потери.
Pэм = Eа · Iа = M · ω0
Энергетическая диаграмма двигателя постоянного тока с параллельным возбуждением.
Pв — потери на возбуждение.
Pэл. а — электрические потери в цепи якоря.
Pмг — магнитные потери, состоящие из потерей на гистерезис и вихревые токи в магнитопроводе машины.
Pмх – механические потери на трение в подшипниках, трении щеток о коллектор, коллектора и якоря о воздух, трение вентилятора о воздух. Механические потери зависят от конструкции машины и для каждого конкретного двигателя будут величиной постоянной.
Pд – добавочные потери, их называют технологическими потерями, так как они связаны с качеством выполнения машины. Добавочные потери учесть трудно, их берут: Pд=0,001·Pн
P1 – первичная электрическая мощность, потребляемая из питающей сети.
P2 – механическая мощность.
P2=M·ω
P2 = P1 — Pв – Pэл. а – Pм2 – Pмх – Pд
ΣP = Pв – Pэл. а – Pм2 – Pмх – Pд
η = P2 / P1 = (P1 – ΣP) / P1 = 1 – (ΣP / P1)
Рабочие характеристики двигателя постоянного тока с параллельным возбуждением Pн=10 кВт, Uн=220 В, nн=950 об/мин.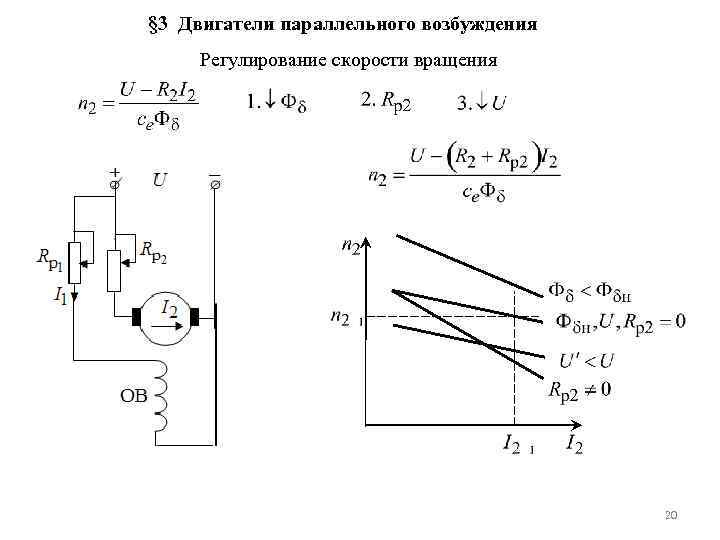
Характеристика ω(P2) будет отличаться для двигателя с независимым и параллельным возбуждениями. Все остальные характеристики будут иметь одинаковый вид для независимого и параллельного возбуждений.
Все рабочие характеристики строятся для интервала полезных мощностей от 0 до 1,25 Pн.
Как видно из кривой КПД, КПД сначала возрастает, затем в районе номинальной мощности достигает максимума и снижается при увеличении полезной мощности. КПД достигает максимума, когда электрические потери равны магнитным потерям.
Электрические потери называются переменными потерями. Магнитные потери называются постоянными потерями. На отрезке кривой КПД от 0 до Pн преобладают магнитные потери, далее начинают преобладать электрические потери.
https://ofild.ru/omsk/uslugi/spa-devichnik
Обзор | Повышение производительности щеточного двигателя постоянного тока
Обзор
Сохранить Подписаться
Пожалуйста, войдите, чтобы подписаться на это руководство.
После входа в систему вы будете перенаправлены обратно к этому руководству и сможете подписаться на него.
Изменение режима работы контроллера двигателя и определение оптимальной частоты ШИМ может значительно улучшить управление и производительность коллекторных двигателей постоянного тока. Используя CircuitPython, установите режим затухания вашего контроллера двигателя с быстрого на медленный и выберите частоту ШИМ ниже 100 Гц для улучшения результатов.
Перейдите к разделу Примеры кода , чтобы узнать, как это делается.
Работает с:
- CRICKIT FeatherWing
- CRICKIT для Circuit Playground Express
- Двигатель постоянного тока + шаговый двигатель FeatherWing
- Мотор/Шаговый/Сервощит
- DRV8871 Вывод драйвера двигателя постоянного тока
- DRV8833 Вывод драйвера постоянного/шагового двигателя
- TB6612 1.2A Драйвер шагового/постоянного тока
- L9110H Драйвер двигателя H-Bridge
- Драйвер двигателя L293D с двойным Н-образным мостом
Вспомогательные библиотеки кода:
- Adafruit Crickit для CircuitPython
- Мотор Adafruit для CircuitPython
- Комплект Adafruit MotorKit для CircuitPython
- Adafruit MotorShield для Arduino
Собранный двигатель постоянного тока + шаговый двигатель FeatherWing Add-on
Feather board без амбиций — это Feather board без FeatherWings! Это полностью собранный (с разъемами) двигатель постоянного тока + шаговый двигатель FeatherWing, который позволит.
..
Комплект Adafruit Motor/Stepper/Servo Shield для Arduino v2
Оригинальный комплект Adafruit Motorshield — один из наших самых любимых наборов, поэтому мы решили сделать что-то еще лучше. Мы улучшили комплект щита, чтобы сделать его лучшим,…
Adafruit CRICKIT FeatherWing для любого Feather
Иногда мы задаемся вопросом, смотрят ли когда-нибудь инженеры-робототехники фильмы. Если бы они это сделали, то знали бы, что превращение роботов в слуг всегда заканчивается бунтом роботов. Зачем вообще спускаться по этому…
Adafruit CRICKIT для Circuit Playground Express
Иногда мы задаемся вопросом, смотрят ли когда-нибудь инженеры-робототехники фильмы. Если бы они это сделали, то знали бы, что превращение роботов в слуг всегда заканчивается бунтом роботов. Зачем вообще спускаться по этому…
Ваш браузер не поддерживает видео тег.Adafruit DRV8833 Разветвительная плата драйвера шагового/постоянного тока
Включите два двигателя постоянного тока или включите один биполярный или однополярный шаговый двигатель с током до 1,2 А на канал с помощью DRV8833.
Этот чип драйвера двигателя является хорошей альтернативой драйверу TB6612. Вот так…
Адаптивная плата драйвера двигателя постоянного тока Adafruit DRV8871 — 3,6 А макс. Этот моторный драйвер имеет множество замечательных характеристик, которые делают его полезным для самых разных…
Ваш браузер не поддерживает видео тег.Adafruit TB6612 Разветвительная плата драйвера шагового/постоянного тока 1,2 А
Включите два двигателя постоянного тока, включите один биполярный или однополярный шаговый двигатель или запустите два соленоида с током 1,2 А на канал с помощью TB6612. Возможно, они более известны как «
Драйвер двигателя с двойным Н-мостом для постоянного тока или шаговых двигателей — 600 мА — L293D
Запустите четыре соленоида, два двигателя постоянного тока или один биполярный или однополярный шаговый двигатель с током до 600 мА на канал с помощью L293D. Возможно, они более известны как «водители в нашем…
». Ваш браузер не поддерживает видео тег.
L9110H Драйвер H-моста для двигателей постоянного тока — 8 DIP
Управляйте двумя соленоидами или одним двигателем постоянного тока с током до 800 мА на канал с помощью сверхпростого драйвера H-моста L9110H. Этот мостовой чип представляет собой корпус с 8 DIP-разъемами, поэтому его легко установить на любой…
Введение
Это руководство было впервые опубликовано 11 апреля 2021 г. Оно было последним обновлено 11 апреля 2021 г.
Эта страница (обзор) последний раз обновлялась 05 апреля 2021 г.
Текстовый редактор на базе tinymce.
Влияние температуры на характеристики двигателя постоянного тока
При использовании двигателей постоянного тока для любого типа применения необходимо учитывать влияние температуры, чтобы правильно использовать двигатель. Производительность изменится при изменении температуры двигателя. При просмотре кривых двигателя постоянного тока пользователь должен задать вопрос: «Эти кривые отображают характеристики двигателя при комнатной температуре или эти кривые иллюстрируют характеристики при максимальной номинальной температуре?» В зависимости от температуры и требуемой рабочей точки на кривой двигателя разница в производительности между «холодными» и «горячими» условиями может быть значительной.
После того, как конструкция двигателя завершена, включая размеры двигателя, магнитную цепь и конфигурацию обмотки двигателя, несколько характеристик, определяющих рабочие характеристики двигателя, становятся «теоретически» фиксированными; постоянная момента (KT), постоянная напряжения (KE) и сопротивление на клеммах двигателя (Rmt). Эти три значения будут определять выходной крутящий момент, скорость двигателя и результирующую выходную мощность в любой точке кривой двигателя при заданном напряжении на клеммах, а также общий наклон кривой двигателя.
Постоянные двигателя НЕ ЯВЛЯЮТСЯ ДЕЙСТВИТЕЛЬНО постоянными
Постоянные крутящего момента и постоянного напряжения определяются на этапе проектирования и являются функцией всей конструкции магнитной цепи. Они всегда равны при использовании единиц СИ. Например, если двигатель KT = 0,1 Нм/А, то двигатель KE = 0,1 В/(рад/с), при условии, что используются Нм и В/(рад/с). Сопротивление клемм двигателя также определяется на этапе проектирования количеством катушек, количеством витков катушки и диаметром магнитного провода.
Эти принципы применимы как к щеточным, так и к бесщеточным двигателям постоянного тока.
Однако фраза «постоянные двигателя» несколько неверна. Сопротивление обмотки и плотность потока постоянного магнита будут изменяться при изменении температуры. По мере увеличения температуры двигателя сопротивление обмотки будет увеличиваться в зависимости от температурного коэффициента меди. Плотность потока постоянных магнитов также будет уменьшаться в зависимости от температуры. Изменения в этих двух ключевых компонентах двигателя приведут к увеличению скорости двигателя на холостом ходу и уменьшению крутящего момента двигателя с заблокированным ротором, изменяя общий наклон кривой двигателя. Как только пользователь поймет эту концепцию, станет ясно, что характеристики двигателя, определенные с помощью быстрого динамометрического теста с двигателем при комнатной температуре, значительно отличаются от характеристик двигателя при работе при максимальной температуре под нагрузкой.
Кривая двигателя постоянного тока
Кривые характеристик двигателя постоянного тока могут быть созданы при различных условиях.
Например, кривая двигателя, показанная на рис. 1, представляет двигатель с разомкнутым контуром, быстро испытанный (для предотвращения нагрева) на динамометрическом стенде. Испытание будет выполняться путем быстрой загрузки двигателя от холостого хода до заторможенного ротора (опрокидывание) с использованием фиксированного напряжения на клеммах источника питания с низким выходным сопротивлением. Такой тест проводится для того, чтобы получить «базовый» показатель производительности двигателя, когда двигатель находится при комнатной температуре. Скорость вала двигателя и ток отображаются как функция крутящего момента двигателя. Из этого теста и нескольких показаний сопротивления можно определить значения постоянной крутящего момента, постоянного напряжения и сопротивления клемм. Эта информация очень полезна для приблизительной оценки основных характеристик двигателя и может быть достаточной для приложения, требующего прерывистой работы с длительным периодом отдыха между каждым рабочим циклом.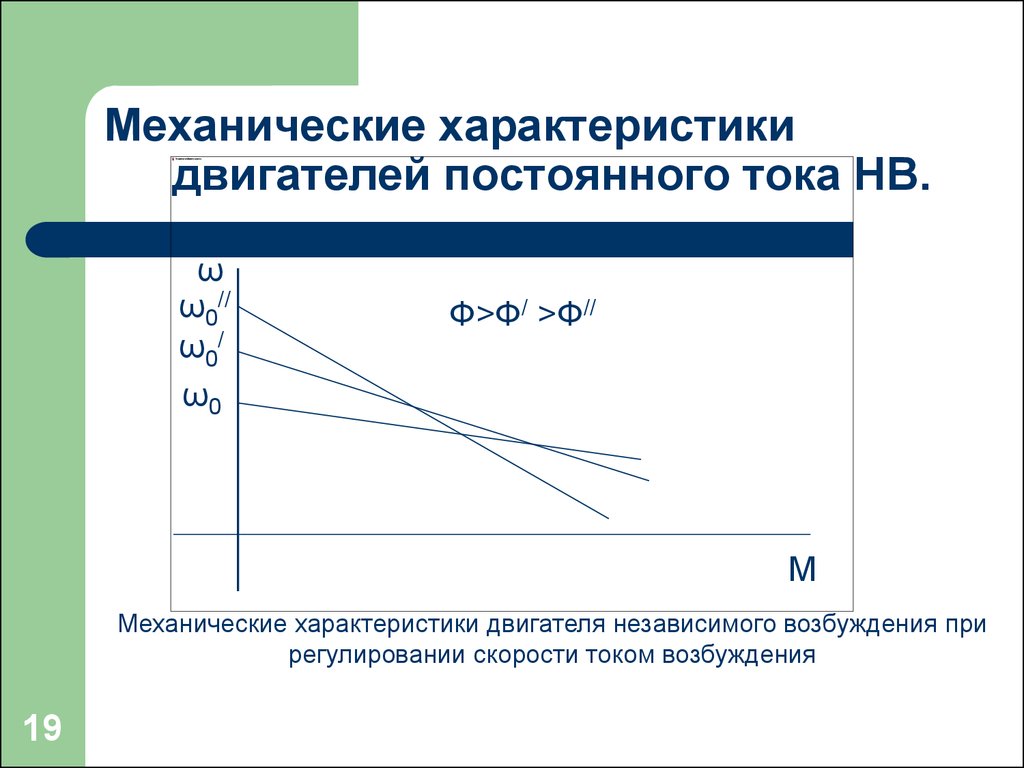
| Рис. 1 Типовая кривая двигателя постоянного тока: быстрое испытание производительности |
В таких приложениях, как повторяющиеся перемещения от точки к точке, приложениях, требующих частых пусков и остановок высокоинерционной нагрузки, или приложениях, требующих, чтобы двигатель вращался в течение длительных периодов времени (например, вентиляторы) данные двигателя, иллюстрирующие работу двигателя при комнатной температуре, неадекватны и могут привести к неправильному использованию двигателя или превышению максимальной номинальной температуры двигателя.
По мере увеличения температуры двигателя сопротивление будет увеличиваться, а константа крутящего момента и константа напряжения уменьшаться. Это приводит к увеличению скорости холостого хода и уменьшению крутящего момента при заблокированном роторе. На рис. 2 показан пример «холодного» и «горячего» режима работы одного и того же двигателя постоянного тока.
Кривая «горячего» двигателя показывает, насколько производительность может измениться при работе двигателя при повышенной температуре.
| Рисунок 2 Производительность: комнатная температура и повышенная температура |
Температурное воздействие сопротивления обмотки двигателя
Сопротивление обмотки двигателя (Rmt) является основной причиной выделения тепла внутри двигателя. Чтобы любой электродвигатель создавал крутящий момент, ток должен проходить через обмотки двигателя. Медь — отличный проводник, однако он не идеален; физика материалов и примеси заставят атомы вибрировать с большей скоростью по мере того, как течет больший ток. Результатом является постоянное повышение температуры обмоток двигателя. Все металлические проводники имеют положительный температурный коэффициент сопротивления. Это означает, что при повышении температуры сопротивление материала также увеличивается в зависимости от типа используемого проводника.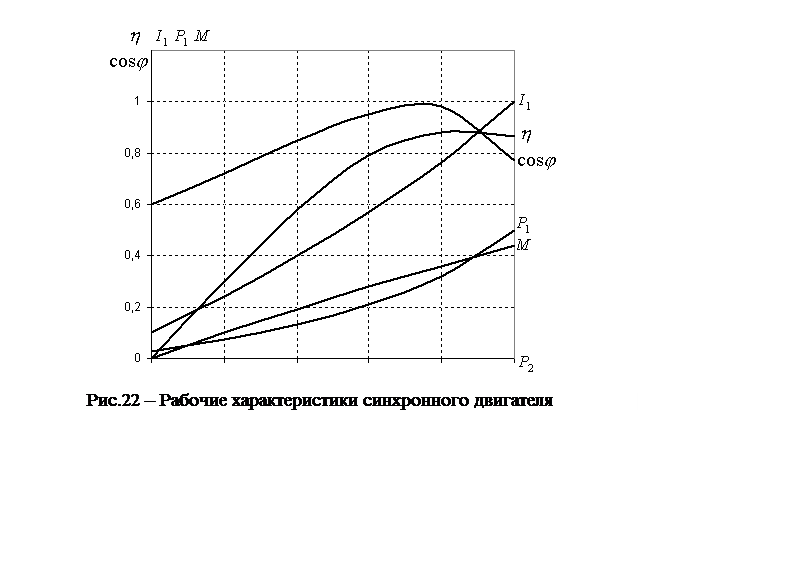
В электродвигателях обычно используется медный проводник, за исключением особых случаев. Во многих беличьих клетках асинхронных двигателей используется литой алюминий для простоты изготовления, но в подавляющем большинстве двигателей используется медный магнитный провод. В таблице 2 перечислены примеры металлов, используемых в электрических и электронных устройствах, и их соответствующие температурные коэффициенты (α).
| Таблица 1. Символы и единицы измерения |
| Таблица 2. Температурные коэффициенты для различных материалов |
Уравнения 1 и 2 иллюстрируют взаимосвязь между температурой обмотки, сопротивлением обмотки и рассеиваемой мощностью.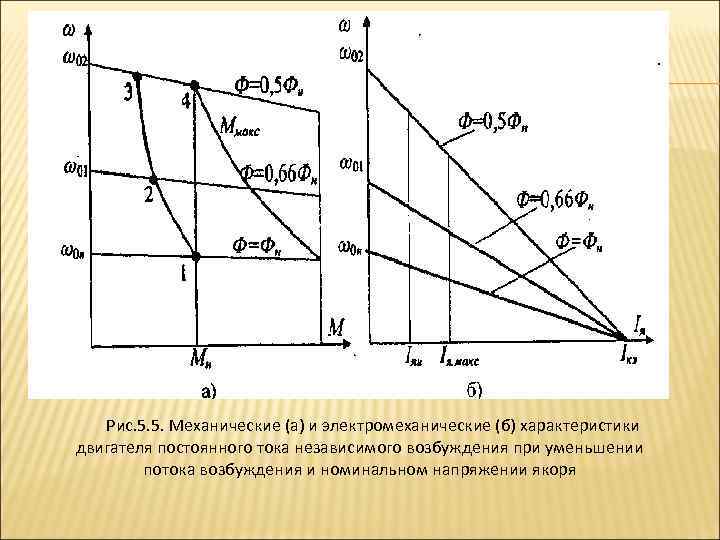
| Уравнение 1. Изменение сопротивления обмотки |
| Уравнение 2. Потери мощности из-за сопротивления обмотки |
Влияние температуры на плотность магнитного потока
Постоянная крутящего момента двигателя (K T ) и константа напряжения (K E ) напрямую связаны с плотностью магнитного потока (B r ) постоянных магнитов. В зависимости от физики используемого магнитного материала общая плотность магнитного потока будет изменяться на заданный процент с увеличением температуры магнита. По мере повышения температуры материала колебания атомов вызывают «рандомизацию» некогда выровненных магнитных моментов, что приводит к уменьшению плотности магнитного потока.
Если предположить, что двигатель работает в заданном расчетном окне, уменьшение плотности потока является временным и начнет восстанавливаться по мере остывания магнита. Однако, если максимальная номинальная температура магнитов превышена, произойдет частичное размагничивание, которое навсегда изменит работу двигателя.
Значения в таблице 3 представляют средние значения для классов материалов. Конкретные марки магнитов в классе материалов будут отличаться от значений, указанных ниже. Например, некоторые сорта неодимовых магнитов могут превышать указанную рабочую температуру в 150°C. В таблице показаны относительные различия между температурными характеристиками различных материалов. Если требуются точные значения, рекомендуется проконсультироваться с инженером по применению на заводе-изготовителе двигателя для получения конкретной информации.
| Таблица 3. Температурные коэффициенты для различных материалов постоянных магнитов |
Уравнение 3.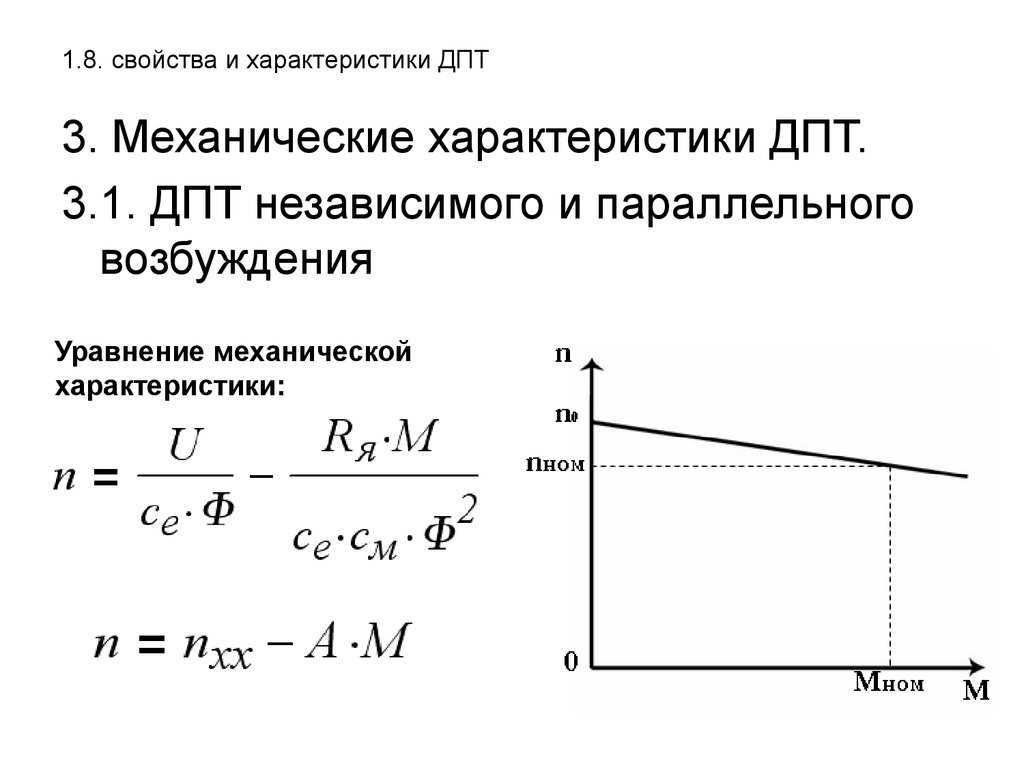 Изменение K T и K E (K T = K E при использовании единиц СИ) 3 |
Пользователи часто задают вопрос о связи КТ и КЭ в результате повышенной температуры. В случае использования единиц СИ одна всегда будет равна другой, и обе будут одинаково меняться с температурой.
В случае использования английских единиц K T и K E выражаются в унциях-дюйм/A (фунт-дюйм/A, фунт-фут/A и т. д.) и В/об/мин. Одно не равно другому при использовании этих единиц, но обе величины будут уменьшаться в одинаковой пропорции с повышением температуры.
Как это влияет на общую производительность двигателя?
При повышенной температуре двигателя наклон кривой двигателя постоянного тока увеличивается в результате увеличения скорости холостого хода и уменьшения крутящего момента заблокированного ротора (иногда называемого крутящим моментом).
На Рисунке 3 ниже показана общая площадь под конкретной кривой двигателя, которую можно рассматривать как диапазон стабильной работы от комнатной температуры до максимальной номинальной температуры двигателя.
| Рис. 3. Характеристики двигателя: «Неиспользуемая» область под кривой характеристик двигателя |
Другим термином, относящимся к наклону кривой двигателя постоянного тока, является «регулирование». Регулирование двигателя описывает, насколько изменится скорость вала при заданном изменении нагрузки на вал при подаче на двигатель фиксированного напряжения на клеммах (при работе в системе с разомкнутым контуром). Более пологая кривая скорость-момент приведет к меньшему изменению скорости вала при увеличении нагрузки. По мере того, как температура двигателя увеличивается и кривая становится более крутой, скорость вращения вала будет падать больше при том же увеличении нагрузки.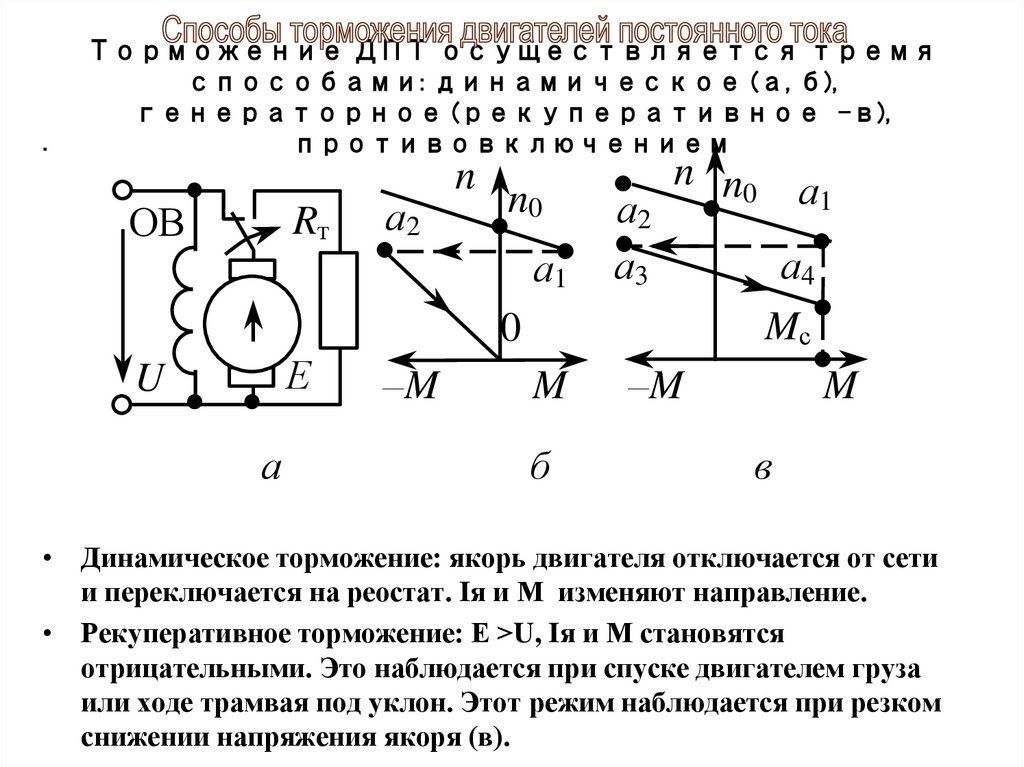
| Уравнение 4а. Теоретическое регулирование двигателя с использованием констант |
| Уравнение 4б. Регулирование двигателя с использованием кривой производительности |
Уравнения 4 и 5 можно использовать, чтобы проиллюстрировать резкое влияние на характеристики двигателя в результате уменьшения магнитного потока и увеличения сопротивления обмотки. Хотя будет увеличиваться скорость двигателя без нагрузки, а также уменьшаться крутящий момент заблокированного ротора, разница между крутящим моментом «холодного» и «горячего» ротора больше по сравнению с разницей между «холодным» и «горячим». -скорость загрузки.
Момент блокировки ротора сильно зависит как от сопротивления (R mt ), так и от постоянной момента (K T ).
Хотя на скорость холостого хода также будет влиять более высокое сопротивление при повышенной температуре, коэффициент сопротивления оказывает гораздо меньшее влияние на скорость холостого хода, поскольку он умножается на ток холостого хода (I 0 ), относительно небольшое число (сравните уравнения 5b и 5c).
| Уравнение 5а. Ротор двигателя заблокирован (опрокидывание) Ток |
| Уравнение 5б. Момент блокировки ротора (остановка) Крутящий момент |
| Уравнение 5c. Скорость двигателя без нагрузки |
Пользователь должен быть осторожным при проектировании системы, чтобы скорость вала соответствовала минимальной спецификации при заданной нагрузке и повышенной температуре двигателя.
В более сложной системе движения с использованием контроллера с обратной связью скорость вала можно регулировать в заданном диапазоне, чтобы она оставалась «фиксированной» при изменении требований к нагрузке. В следующем примере предполагается, что двигатель работает без обратной связи с регулируемым напряжением на клеммах постоянного тока.
Насколько могут измениться характеристики двигателя при заданных условиях?
| Условия: |
|
Рис. 4. Начальная производительность двигателя при 25°C |
При стабилизированном повышении температуры якоря на 100°C сопротивление на выводах будет выше, а плотность магнитного потока будет ниже по сравнению с начальной температурой двигателя 25°C. Это приведет к изменению R мт , К Т и К Е .
Важное примечание – В приведенных ниже расчетах предполагается, что температуры постоянного магнита и обмотки якоря идентичны. Якорь двигателя, являющийся частью машины, по которой проходит электрический ток, всегда будет иметь более высокую температуру, чем постоянные магниты. На практике фактическое изменение K T , K E и регулирование двигателя будет менее выраженным, чем показано в следующем примере.
Расчетные характеристики двигателя при повышенной температуре 125°C
| Увеличенное сопротивление на клеммах |
| R mt(f) = R mt(i) x [1 + α проводник (Ѳf — Ѳ i )] R mt(f) + x Ом 0,0040 (125°C — 25°C)] R mt(f) = 0,83 Ом |
| Пониженный крутящий момент и постоянное напряжение |
| (K используется как для K E , так и для K T в единицах СИ) )] K ( f ) = 0,071 В/(рад/с) x [1 + (-0,0020)(125°C — 25°C)] K ( f ) = 0,057 В/(рад/с) с) или Нм/А |
| Уменьшенный ток блокировки ротора (остановка) |
| I LR = V T / R mt(f) I LR = 24 В/0,83 Ом I LR = 28,92 А | А
| |
| Уменьшенный крутящий момент заблокированного ротора (опрокидывание) |
| T LR = ILR x K T(f) T LR = 28,92 A x 0,057 Нм/A T LR = 9017 Нм |
| Повышенная скорость без нагрузки |
| N 0 = 9,5493 x [(V T — I 0 x R MT (F) ) / K E (F) ] n ) / K E (F) ] N 0.  8 0. 0. 8 0. 8 0. 0. 8 0. 0. 0. 0. 0. . – 0,30 А x 0,83 Ом) / 0,057 В/(рад/с)] |
| Усиленный двигатель |
| R м = п 0 / T LR R м = 3979 об/мин / 1,65 Нм R м = 2412 об/мин / Нм |
| Таблица 4. Изменение характеристик двигателя |
| Рис. 5. Сравнение характеристик двигателя при 25°C и 125°C |
Интересно отметить, насколько производительность меняется при заданном повышении температуры двигателя. Хотя анализ полезен для понимания явления, он ни в коем случае не идеален.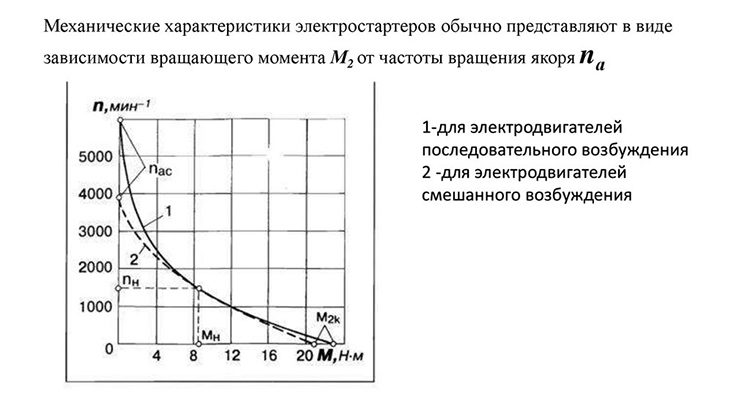
Например, следует помнить несколько вещей…
|
Однако приведенный выше анализ в первом приближении очень полезен для применения двигателя и понимания его ограничений в конкретном приложении.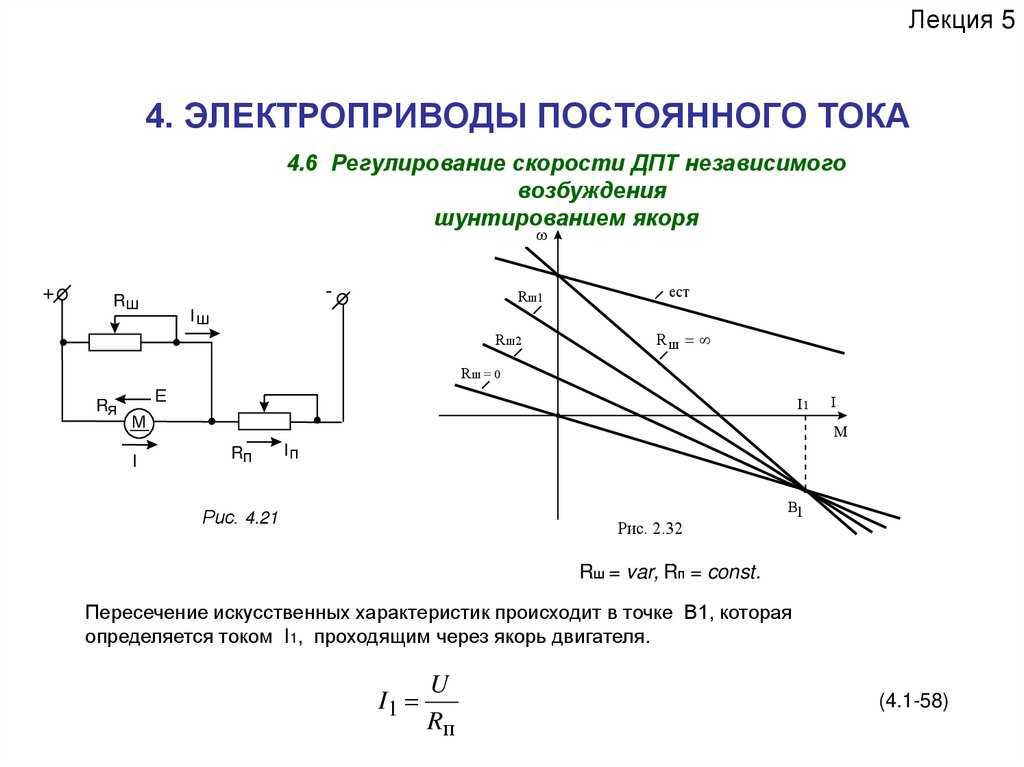
Постоянные двигателя и максимальная выходная мощность
Редко, если вообще когда-либо, двигатель работает на максимальной мощности очень долго. За исключением очень маленьких двигателей малой мощности, большинство из них не могут работать непрерывно при максимальной мощности без превышения номинальной температуры. Приведенные ниже уравнения можно использовать для определения мощности в любой точке кривой двигателя 9.0102 и максимальной выходной мощности.
| Уравнение 6а. Выходная мощность двигателя (в любой точке) |
| Уравнение 6б. Максимальная выходная мощность двигателя |
| Уравнение 6c. Максимальная выходная мощность двигателя (теоретическая) |
Уравнения 6b и 6c иллюстрируют влияние сопротивления двигателя на выходную мощность машины.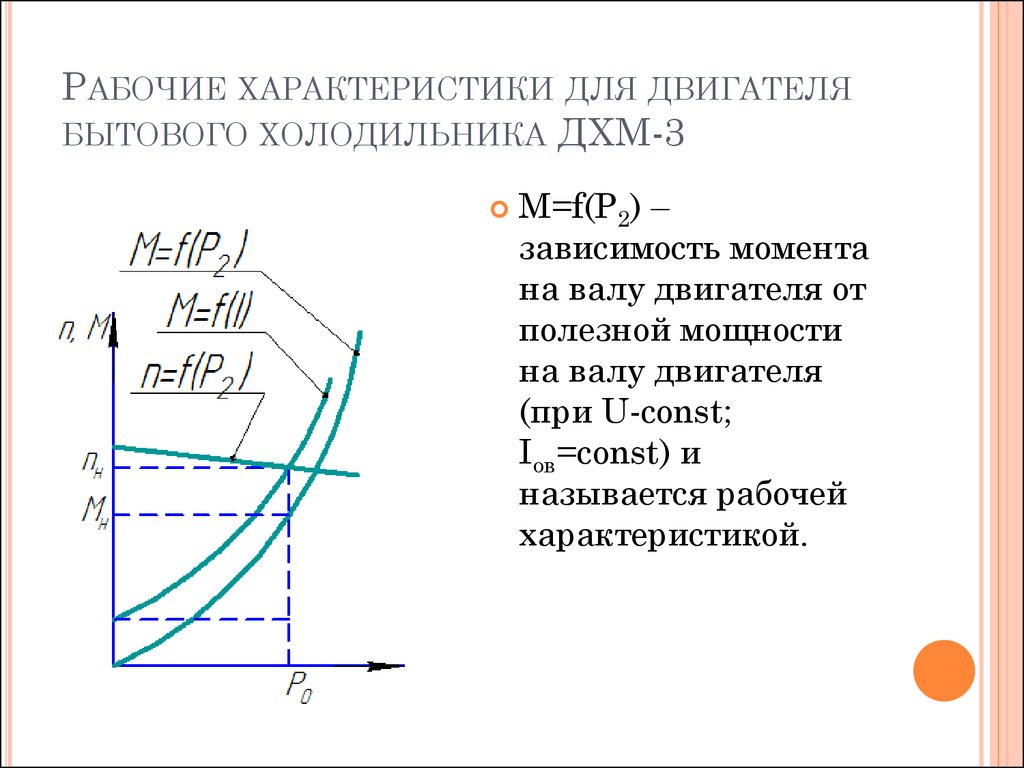
Хотя это не интуитивно понятно, глядя на уравнение 6b, более высокое сопротивление обмотки при повышенной температуре является основной причиной снижения максимальной выходной мощности двигателя. Несмотря на то, что плотность магнитного потока при повышенной температуре уменьшается, уменьшение TLR (из-за уменьшения KT) компенсируется увеличением ω0 (из-за уменьшения KE). Если бы сопротивление осталось прежним, то даже уменьшение плотности магнитного потока существенно не изменило бы максимальную выходную мощность машины.
В действительности, более высокое сопротивление (R mt ) в сочетании с уменьшенной плотностью магнитного потока (более низкая K T ) снижает заторможенный крутящий момент ротора намного больше, чем просто уменьшение плотности магнитного потока, что объясняет уменьшение по максимальной выходной мощности.
| Максимальная выходная мощность при 25°C |
| P макс(i) = 0,25 x ω 0 x T LR P макс(i) = 0,25 x 331 рад/с x 2,88 Нм P макс(i) = 238 Вт |
| Максимальная выходная мощность при 125°C |
| P MAX (F) = 0,25 x ω 0 x T LR P MAX = 0,25 x 417 RAD/S X 1,65 NM 248.  902 (F) P = 0,25 x 417 RAD/S X 1,65 NM . |
Максимальная мощность при повышенной температуре составляет примерно 70% от максимальной мощности при комнатной температуре. Это значительное изменение, и оно является прямым следствием увеличения сопротивления двигателя. Уравнение 6c даст результаты, которые находятся в пределах 1 или 2% от приведенных выше чисел. Это уравнение очень полезно для быстрой оценки максимальной мощности любого двигателя постоянного тока.
| Рис. 6. Максимальная мощность при 25°C и 125°C |
Опубликованные данные. Кривые двигателя бывают разных видов!
Большинство графиков характеристик двигателей постоянного тока содержат как минимум 2 кривые; скорость по отношению к крутящему моменту и ток по отношению к крутящему моменту.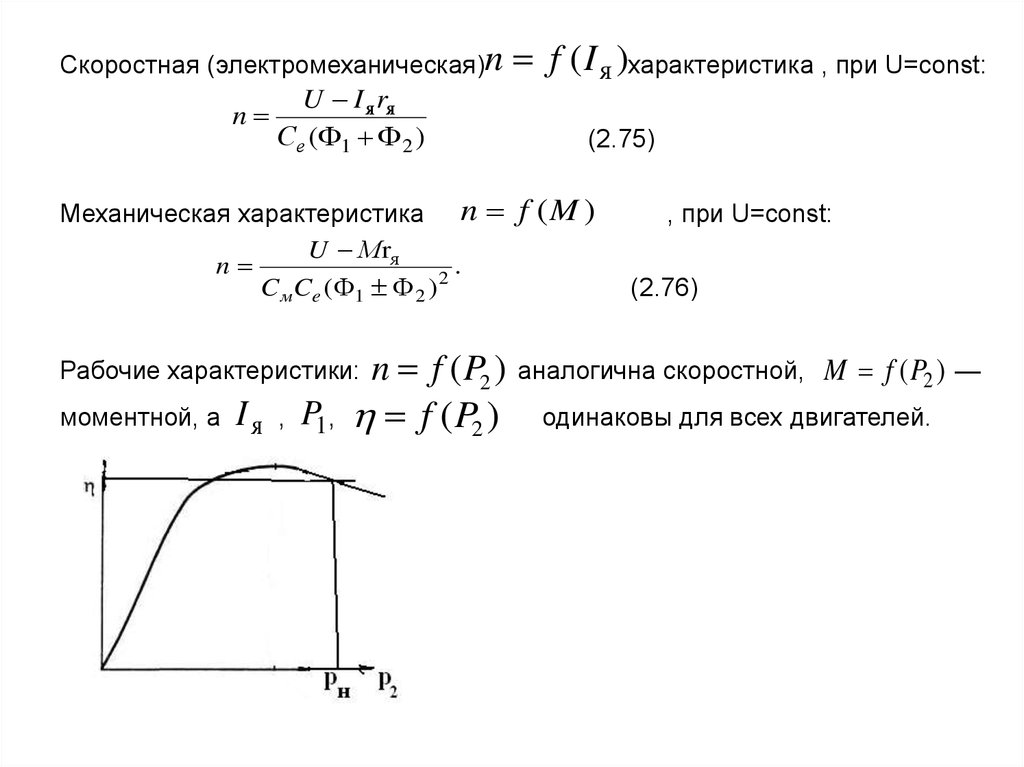
Производители могут решить отображать информацию немного по-другому, а также предоставлять другую информацию, такую как выходная мощность и кривые эффективности.
Пример кривой двигателя, показанный на рис. 1, исключает все другие переменные и предполагает, что двигатель испытывается при фиксированном напряжении на клеммах с использованием источника питания с низким импедансом и постепенно нагружается динамометром. Тест выполняется как можно быстрее, чтобы свести к минимуму повышение температуры двигателя. Если испытуемый двигатель представляет собой небольшой двигатель мощностью менее дробных лошадиных сил, динамометр может нагружать двигатель до тех пор, пока скорость вала не достигнет нуля или близкой к нулю оборотов в минуту. В случае более крупных двигателей динамометр может быть настроен на постепенную нагрузку двигателя приблизительно до точки максимальной мощности. Затем можно экстраполировать оставшуюся часть кривой. Полученные данные в любом случае представляют собой (теоретически) линейные зависимости скорости от крутящего момента и тока от крутящего момента.
Некоторые производители, в частности те, которые поставляют комплектные сервосистемы, могут представлять кривые производительности как «смесь» информации, которая включает ограничения на системном уровне. Рассматриваемые ограничения могут включать множество факторов, таких как допустимый постоянный ток, допустимый пиковый ток, ограничения мощности привода/усилителя, максимальное напряжение на шине постоянного тока, максимальная номинальная температура двигателя, насыщение двигателя и механические ограничения скорости. Многие производители могут отображать крутящий момент двигателя по оси «Y», а скорость — по оси «X». Примеры кривых на рисунках 7a и 7b показывают, как могут выглядеть данные, если учитывать такие факторы, как максимальная скорость вращения, максимальное повышение температуры и пиковый ток привода. Независимо от того, как публикуются данные или какие другие системные факторы учитываются, параметры двигателя R mt , K T и K E имеют решающее значение для понимания истинных возможностей двигателя.
| Рисунок 7а. Получение производительности «системы»: повышение температуры в установившемся режиме и ограничения системы |
| Рисунок 7б. Ось крутящего момента и скорости на рис. 7a перевернута |
Еще один фактор, который следует учитывать при оценке различных кривых производительности, заключается в том, что фактические условия испытаний не всегда могут быть очевидными. Разные поставщики будут публиковать разную информацию. В случае, когда двигатели быстро тестируются на динамометре (чтобы свести к минимуму повышение температуры), этот метод имеет тенденцию быть очень последовательным и обеспечивает хороший базовый уровень. Недостатком является то, что результаты не представляют наихудшие условия.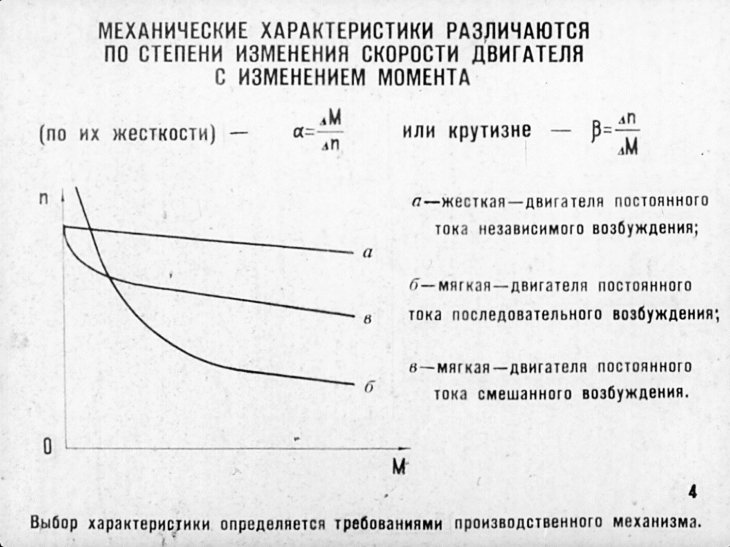
Если двигатели испытываются при максимальной номинальной температуре, пользователь лучше поймет возможности двигателя при использовании в приложениях, где температура двигателя стабилизируется на значении, значительно превышающем комнатную температуру. Недостатком является то, что существует множество других переменных, которые могут исказить результаты испытаний, такие как метод измерения температуры, монтаж двигателя (вызывающий эффект теплоотвода), поток воздуха вокруг двигателя и т. д. Некоторые производители двигателей испытывают свои двигатели при наихудших условиях. состояние корпуса; двигатель, стабилизированный до полной номинальной температуры без теплоотвода или принудительного воздушного потока. Не существует строгих правил, определяющих, как производитель должен представлять данные о производительности. При оценке информации важно помнить, что нужно задавать правильные вопросы.
Общая конструкция двигателя и теплопередача
Механическая конструкция влияет на характеристики теплопередачи в двигателе.
В двигателе постоянного тока с механическим коммутатором и щетками медные обмотки намотаны в пазах вокруг «вращающейся» части двигателя (называемой якорем). Тепло, выделяемое медными обмотками якоря, будет проходить через пластины якоря к валу двигателя и подшипниковой системе. Благодаря конвекции тепло также будет мигрировать через воздушный зазор к постоянным магнитам и корпусу, где оно в конечном итоге будет рассеиваться в окружающей среде. Несмотря на то, что некоторая часть теплопередачи происходит за счет прямой передачи через пакет ламинирования к подшипниковой системе и корпусу, большая часть генерируемого тепла будет проходить через воздушный зазор и через магниты.
В случае бесщеточного двигателя постоянного тока медные обмотки намотаны в пазах (в щелевом бесщеточном двигателе) или сформированы против магнитного сердечника (в бесщелевом бесщеточном двигателе) и выполнены как часть внутренней поверхности корпуса двигателя. . Эта конструкция обеспечивает прямой путь теплопроводности от выделяющей тепло меди к корпусу двигателя, где она будет рассеиваться в окружающую среду.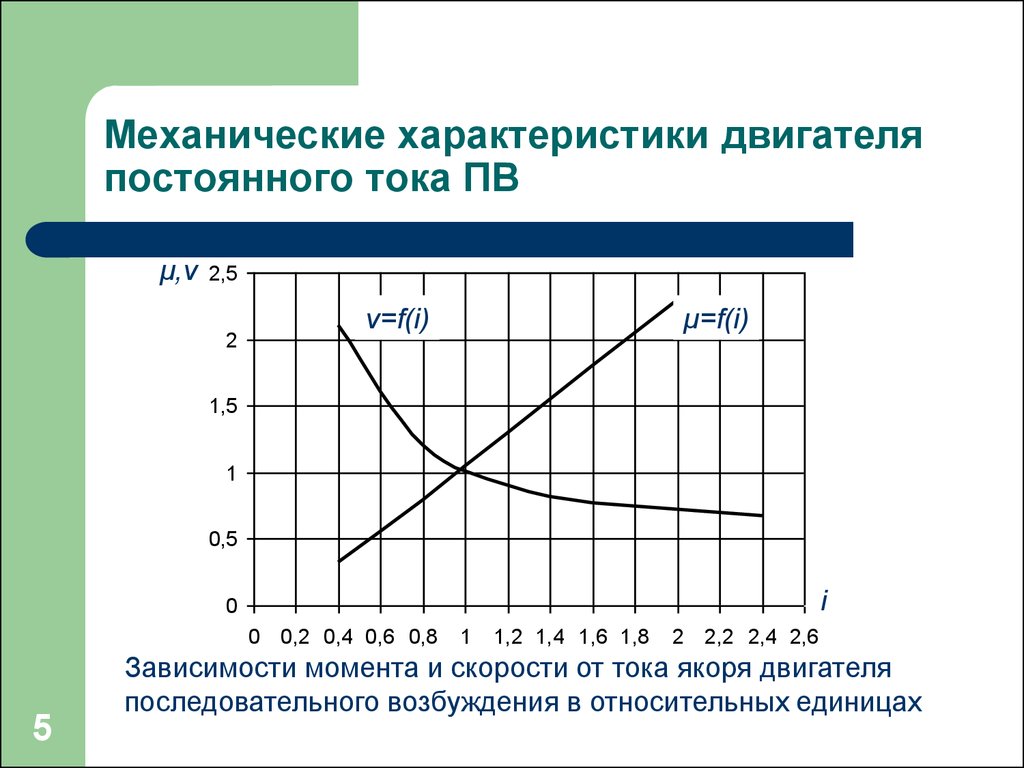
Постоянные магниты в бесщеточном двигателе находятся на вращающейся части машины.
В любом случае будет очень трудно, если вообще возможно, предсказать повышение температуры отдельных компонентов без эмпирического тестирования, но одно можно сказать наверняка; повышение температуры отдельных компонентов (горячих точек внутри двигателя) будет разным для щеточного и бесщеточного двигателей при прочих равных условиях.
Нет альтернативы прикладным испытаниям
Целью предыдущего обсуждения и примеров расчета является лучшее понимание того, как производительность двигателя изменяется в зависимости от температуры. Ничто не заменит тестирование и проверку двигателя в условиях эксплуатации. Надлежащая теоретическая обработка невозможна из-за большого количества задействованных переменных и допущений, однако примеры расчетов могут служить в качестве первого приближения для получения представления о величине возможных изменений.
Наилучший способ понять характеристики двигателя в реальных условиях эксплуатации — максимально точно смоделировать приложение, одновременно собирая данные о температуре с течением времени с помощью системы сбора данных.
