Расчет частоты lc контура. Колебательный контур: принцип работы, резонанс и применение

Что такое колебательный контур и как он работает. Какие бывают виды колебательных контуров. Как рассчитать резонансную частоту контура. Где применяются колебательные контуры в электронике.

Что такое колебательный контур

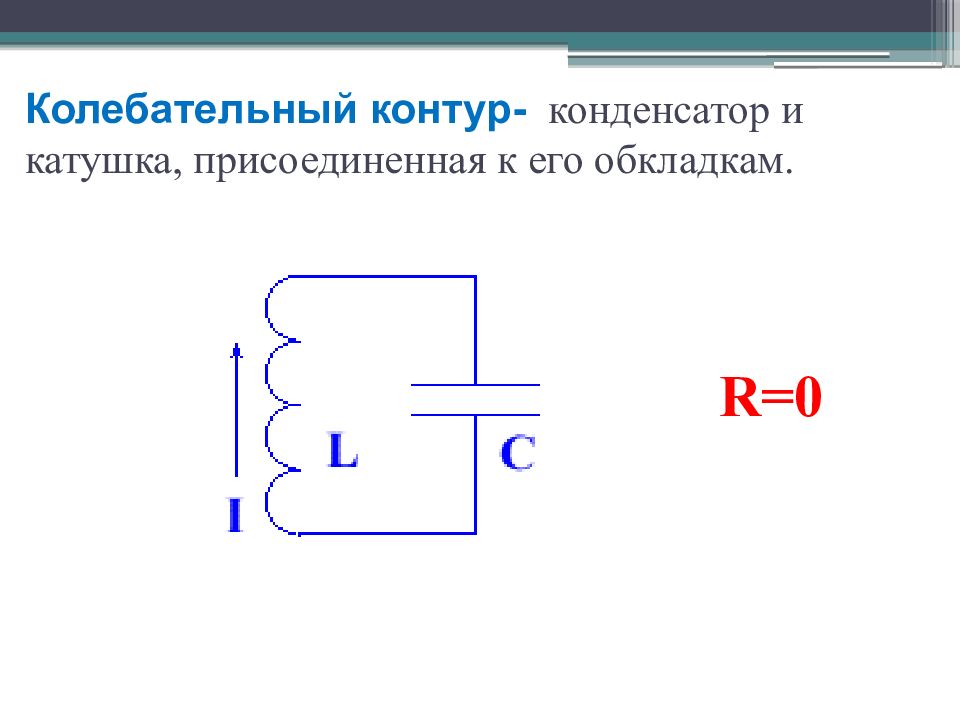
Колебательный контур — это электрическая цепь, состоящая из катушки индуктивности (L) и конденсатора (C), соединенных последовательно или параллельно. В таком контуре могут возникать электромагнитные колебания, при которых энергия периодически переходит из электрического поля конденсатора в магнитное поле катушки и обратно.

Основные характеристики колебательного контура:

• Резонансная частота — частота, на которой амплитуда колебаний максимальна
• Добротность — характеризует, насколько слабо затухают колебания в контуре
• Полоса пропускания — диапазон частот вблизи резонансной, в котором контур эффективно пропускает сигнал

Принцип работы колебательного контура

Работа колебательного контура основана на обмене энергией между электрическим полем конденсатора и магнитным полем катушки. Рассмотрим последовательность процессов:

1. Изначально конденсатор заряжен, вся энергия сосредоточена в его электрическом поле
2. Конденсатор начинает разряжаться через катушку, создавая в ней ток
3. Ток в катушке создает магнитное поле, энергия переходит в него
4. Когда конденсатор полностью разрядится, вся энергия окажется в магнитном поле катушки
5. Магнитное поле катушки начнет убывать, наводя ЭДС самоиндукции
6. ЭДС самоиндукции заряжает конденсатор, но уже с противоположной полярностью
7. Процесс повторяется, образуя электромагнитные колебания

Как рассчитывается период колебаний в идеальном контуре? Для этого используется формула Томсона:

T = 2π√(LC)

Где T — период колебаний, L — индуктивность катушки, C — емкость конденсатора.

Виды колебательных контуров

Выделяют два основных вида колебательных контуров:

Последовательный колебательный контур

В последовательном контуре катушка и конденсатор соединены последовательно. Его особенности:

• При резонансе имеет минимальное сопротивление
• Ток в ветвях одинаковый, а напряжения на элементах складываются
• Используется как режекторный фильтр для подавления определенных частот

Параллельный колебательный контур

В параллельном контуре катушка и конденсатор соединены параллельно. Его особенности:

• При резонансе имеет максимальное сопротивление
• Напряжение на элементах одинаковое, а токи в ветвях складываются
• Используется как полосовой фильтр для выделения определенных частот

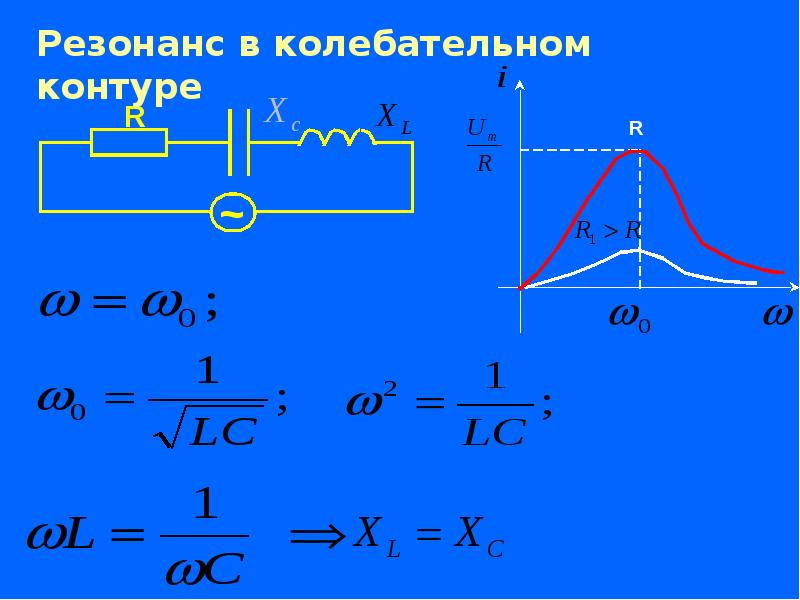
Резонанс в колебательном контуре

Резонанс — это явление резкого возрастания амплитуды колебаний при совпадении частоты внешнего воздействия с собственной частотой контура. При резонансе:

• Амплитуда колебаний достигает максимума
• Реактивные сопротивления катушки и конденсатора компенсируют друг друга
• В цепи остается только активное сопротивление

Как рассчитать резонансную частоту контура? Для этого используется формула:

f = 1 / (2π√(LC))

Где f — резонансная частота, L — индуктивность, C — емкость.

Применение колебательных контуров

Колебательные контуры широко используются в радиотехнике и электронике:

• В радиоприемниках для настройки на нужную частоту
• В генераторах электромагнитных колебаний
• В фильтрах для выделения или подавления определенных частот
• В системах беспроводной передачи энергии
• В измерительных приборах

Расчет параметров колебательного контура

При проектировании колебательных контуров важно уметь рассчитывать их основные параметры. Рассмотрим основные формулы:

Расчет резонансной частоты

Резонансная частота f0 рассчитывается по формуле:

f0 = 1 / (2π√(LC))

Где L — индуктивность в Генри, C — емкость в Фарадах.

Расчет добротности контура

Добротность Q можно рассчитать по формуле:

Q = (1/R) * √(L/C)

Где R — активное сопротивление контура в Омах.

Расчет полосы пропускания

Полоса пропускания Δf определяется как:

Δf = f0 / Q

Где f0 — резонансная частота, Q — добротность контура.

Как настроить колебательный контур

Настройка колебательного контура на нужную частоту производится следующими способами:

1. Изменение емкости конденсатора (переменный конденсатор)
2. Изменение индуктивности катушки (катушка с отводами)
3. Подстройка сердечника катушки
4. Изменение взаимной индуктивности связанных контуров

При настройке важно учитывать паразитные параметры элементов схемы, которые могут влиять на резонансную частоту.

Моделирование колебательных контуров

Для анализа работы колебательных контуров широко применяется компьютерное моделирование. Популярные программы для моделирования:

• SPICE — универсальный симулятор электронных схем
• MATLAB — мощный инструмент для математического моделирования
• LabVIEW — среда разработки виртуальных приборов

Моделирование позволяет:

• Рассчитать частотные характеристики контура
• Определить оптимальные параметры элементов
• Исследовать переходные процессы
• Оценить влияние паразитных параметров

Проблемы реальных колебательных контуров

В реальных колебательных контурах возникает ряд проблем, которые необходимо учитывать:

• Потери энергии из-за активного сопротивления элементов
• Паразитные емкости и индуктивности
• Нелинейность параметров элементов
• Влияние температуры на характеристики
• Взаимное влияние близко расположенных контуров

Для минимизации этих проблем применяются следующие методы:

• Использование элементов с высокой добротностью
• Экранирование контуров
• Температурная компенсация
• Точный расчет и моделирование

Перспективы развития колебательных контуров

Несмотря на то, что колебательные контуры известны давно, они продолжают развиваться. Основные направления развития:

• Миниатюризация контуров для применения в микроэлектронике
• Использование новых материалов с улучшенными характеристиками
• Применение в системах беспроводной передачи энергии
• Разработка перестраиваемых контуров с электронным управлением
• Интеграция с цифровыми системами обработки сигналов

Таким образом, колебательные контуры остаются важным элементом современной электроники, находя все новые области применения.

Калькулятор параллельного колебательного LC-контура

Конденсаторы Индуктивные компоненты Измерительные приборы

Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L, обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром. В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот. Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное — растет. При некоторой частоте ƒ₀, емкостное сопротивление конденсатора и индуктивное сопротивление катушки становятся численно равными: Xc = XL. При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний.

Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве емкостного и индуктивного сопротивлений, называют режимом резонанса токов. Явление резонанса токов используется в полосовых фильтрах для выделения определенной частоты. Такая схема необходима для работы телевизора, радиоприемника, ёмкостного генератора и т.п.

Расчет частоты резонанса параллельного LC-контура описывается формулами:

X_L =

2πƒL

X_C =

1

 

2πƒC

ƒ₀ =

1

 

2π√LC

X_L — индуктивное реактивное сопротивление, Ом;

X_С — ёмкостное реактивное сопротивление, Ом;

ƒ₀ — резонансная частота, Гц;

Расчет частоты резонанса LC-контура

Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура, или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.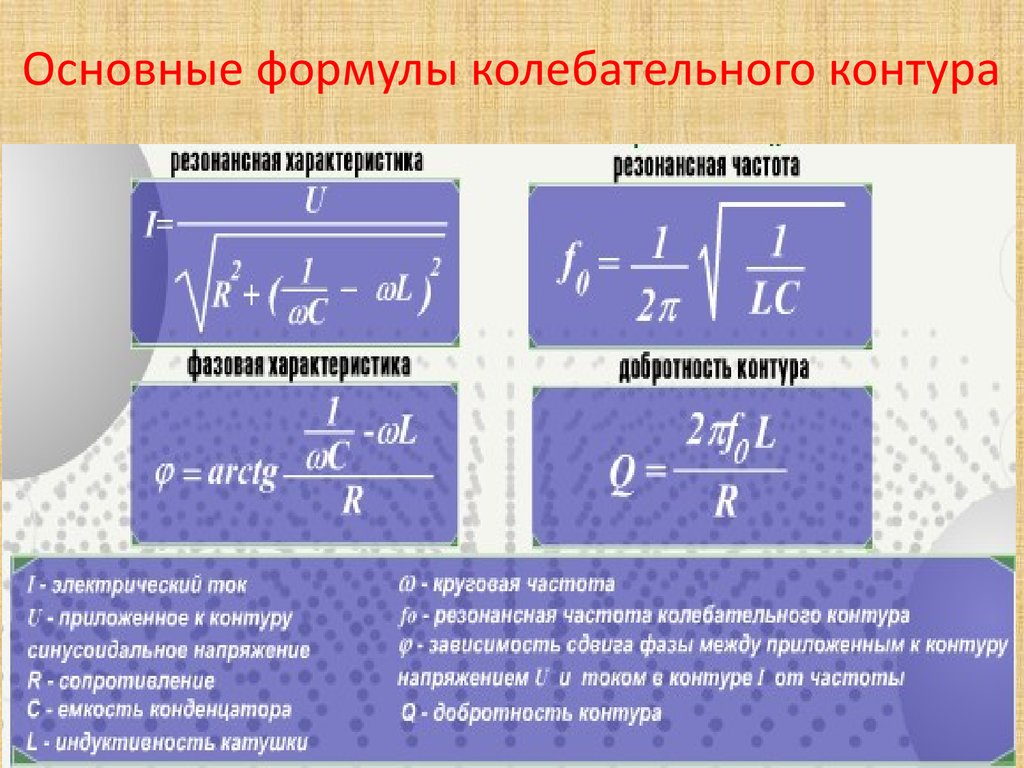

IC

IL

Iƒ

мкФнФпФ

ГнмГнмкГн

МГцкГцГц

X_L = X_C = ƒ₀ = φ = °

X_L > X_C Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного. Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°

Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс, тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.

Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…
Для подбора компонентов будет использована серия E12.

Подбор конденсатора на сайте

Подбор катушки индуктивности на сайте

Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!

Последовательный колебательный контур — Резонанс напряжений

Последовательный колебательный контур обозначение на схеме

Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.

Идеальный последовательный колебательный контур

 На схемах идеальный последовательный колебательный контур обозначается вот так:

где

L — индуктивность, Гн

С — емкость, Ф

Реальный последовательный колебательный контур

Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:

R  — это суммарное сопротивление потерь катушки и конденсатора

L — собственно сама индуктивность катушки

С — собственно сама емкость конденсатора

Принцип работы последовательного колебательного контура

Генератор частоты и последовательный колебательный контур

Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:

Генератор (Ген)у нас будет выдавать синус.

Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.

А вот и сама схема в реальности:

Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.

Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта U_ш , а также снимая осциллограмму с самого генератора U_ГЕН.

С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.

Влияние частоты генератора на сопротивление колебательного контура

В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.

Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.

Частота 200 Герц с копейками:

Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый

Добавляем частоту. 600  Герц с копейками

Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.

Добавляем частоту. 2 Килогерца

Сила тока стала еще больше.

3 Килогерца

Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.

4,25 Килогерц

Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.

И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.

Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.

Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.

Увеличиваем частоту еще больше

Сила тока начинает падать, а сдвиг фаз увеличивается.

22 Килогерца

74 Килогерца

Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.

Резонанс последовательного колебательного контура

Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:

Это явление носит название резонанса.

Не будем углубляться  в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.

Как вы помните, если у нас сопротивление  становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.

Формула Томсона (резонанса) для последовательного колебательного контура

Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора X_L=X_C , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:

Реактивное сопротивление конденсатора вычисляется по формуле:

Приравниваем обе части и вычисляем отсюда F:

В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.

Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.

Замеряем индуктивность катушки:

И замеряем нашу емкость:

Высчитываем по формуле нашу резонансную частоту:

У меня получилось 5, 09 Килогерц.

С помощью  регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)

Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол 😉

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как  среднеквадратичное напряжение  будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Добротность последовательного колебательного контура

Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:

Давайте посчитаем добротность в нашем случае.

Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала  генератора частоты 2 Вольта.

А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.

Считаем по формуле добротности:

Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.

Есть также вторая формула для вычисления добротности.

где

R — сопротивление потерь в контуре, Ом

L — индуктивность, Генри

С — емкость, Фарад

Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.

Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.

Видео на тему «Как работает колебательный контур. Резонанс»:

Резюме

Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.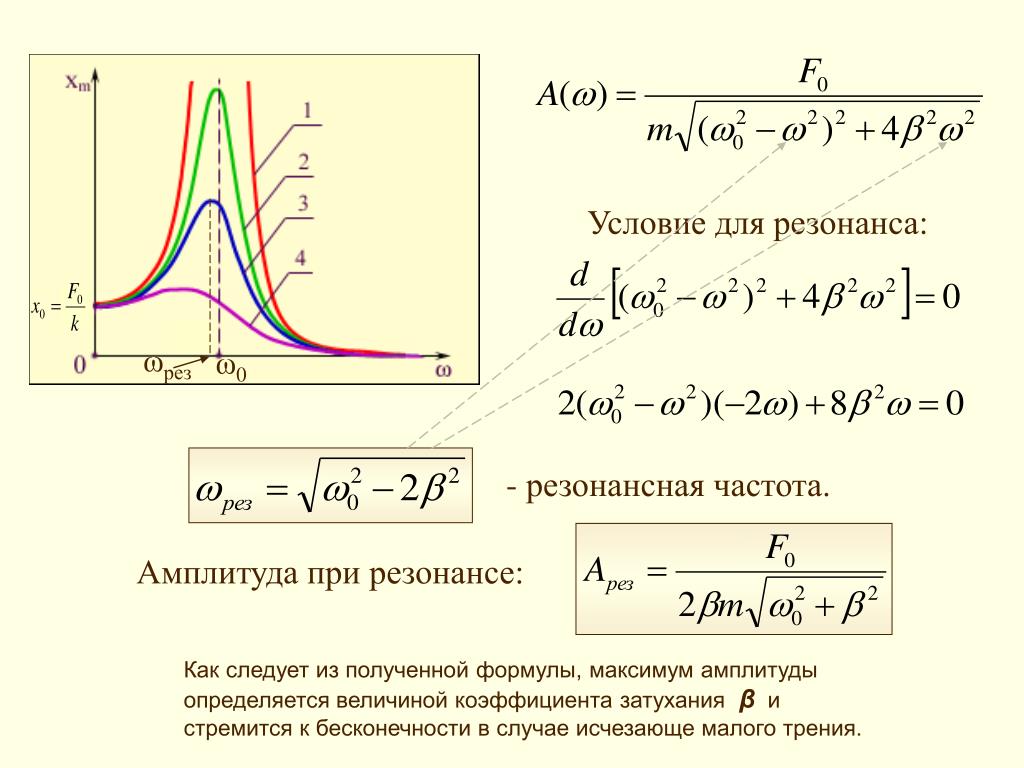

Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.

На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.

При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.

При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.

При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.

Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.

На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.

14.5 Колебания в LC-контуре – University Physics Volume 2

Глава 14. Индуктивность

Цели обучения

К концу этого раздела вы сможете:

• Объяснять, почему заряд или ток колеблются между конденсатором и индуктивностью, соответственно, при последовательном соединении
• Опишите взаимосвязь между зарядом и током, колеблющимся между конденсатором и катушкой индуктивности, соединенными последовательно

Стоит отметить, что и конденсаторы, и катушки индуктивности хранят энергию в своих электрических и магнитных полях соответственно. Цепь, содержащая катушку индуктивности ( L ) и конденсатор ( C ), может колебаться без источника ЭДС, перемещая энергию, хранящуюся в цепи, между электрическим и магнитным полями. Таким образом, концепции, которые мы развиваем в этом разделе, непосредственно применимы к обмену энергией между электрическим и магнитным полями в электромагнитных волнах или свете. Мы начнем с идеализированной цепи с нулевым сопротивлением, которая содержит катушку индуктивности и конденсатор, 9{2}}{С}.[/латекс]

Когда переключатель замкнут, конденсатор начинает разряжаться, создавая ток в цепи. Ток, в свою очередь, создает магнитное поле в индукторе. Конечным результатом этого процесса является передача энергии от конденсатора с его уменьшающимся электрическим полем к индуктору с его увеличивающимся магнитным полем.

Рисунок 14.16  (a–d) Колебания накопления заряда при изменении направления тока в LC-цепи. д) На графиках показано распределение заряда и тока между конденсатором и катушкой индуктивности. 9{2}.[/латекс]

После достижения своего максимума [латекс]{I}_{0},[/латекс] ток i(t) продолжает переносить заряд между обкладками конденсатора, тем самым перезаряжая конденсатор. Поскольку индуктор сопротивляется изменению тока, ток продолжает течь, даже если конденсатор разряжен. Этот непрерывный ток заставляет конденсатор заряжаться с противоположной полярностью. Электрическое поле конденсатора увеличивается, а магнитное поле индуктора уменьшается, и общий эффект заключается в передаче энергии от индуктора 9.0017 обратно на конденсатор. Согласно закону сохранения энергии, максимальный заряд, который вновь приобретает конденсатор, равен [латекс]{q}_{0}.[/латекс] Однако, как показано на рис. 14.16(в), пластины конденсатора заряжены против . к тому, чем они были изначально.

При полной зарядке конденсатор снова передает свою энергию катушке индуктивности, пока снова не разрядится полностью, как показано на рис. 14.16(d). Затем в последней части этого циклического процесса энергия возвращается к конденсатору, и восстанавливается исходное состояние цепи. 9{2}\text{/}2[/латекс]. При отсутствии трения в системе масса-пружина колебания продолжались бы бесконечно. Точно так же колебания цепи LC без сопротивления будут продолжаться вечно, если их не беспокоить; однако эта идеальная схема LC с нулевым сопротивлением непрактична, и любая схема LC будет иметь по крайней мере небольшое сопротивление, которое со временем будет излучать и терять энергию.

Частота колебаний без сопротивления 9{2}.[/латекс]

Эквивалентность двух систем очевидна. Чтобы перейти от механической системы к электромагнитной, мы просто заменим m на L , v на i , k на 1/ C и x на 900. 17 кв . Теперь x(t) равно

.

[латекс] х \ влево (т \ вправо) = А \ фантом {\ правило {0.2em} {0ex}} \ текст {cos} \ влево (\ омега т + \ varphi \ вправо) [/латекс]

, где [латекс]\омега =\sqrt{k\текст{/}м}.[/латекс] Следовательно, заряд конденсатора в Цепь LC задается

[латекс] q \ влево (т \ вправо) = {q} _ {0} \ фантом {\ правило {0.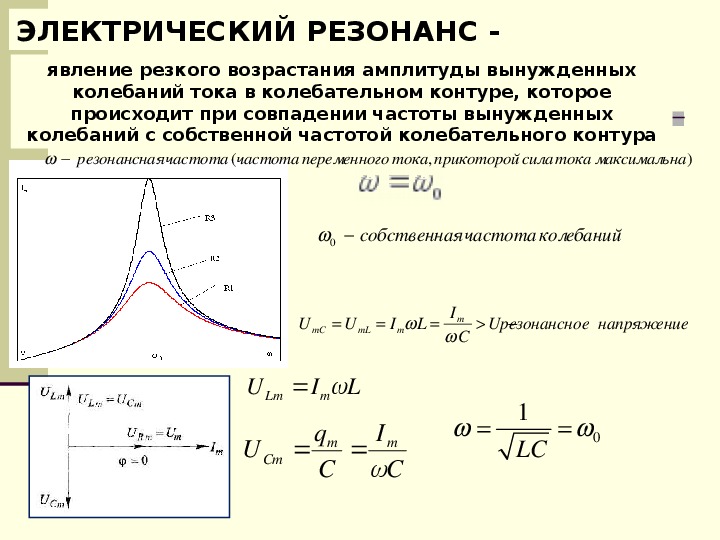 2em} {0ex}} \ текст {cos} \ влево (\ омега т + \ varphi \ вправо) [ /латекс]

где угловая частота колебаний в контуре

[латекс]\омега =\sqrt{\frac{1}{LC}}.[/латекс]

Наконец, ток в цепи LC находится путем взятия производной по времени от q(t) :

[латекс] я \ влево (т \ вправо) = \ гидроразрыва {dq \ влево (т \ вправо)} {дт} = \ текст {-} \ омега {q} _ {0} \ фантом {\ правило {0,2 em}{0ex}}\text{sin}\left(\omega t+\varphi \right).[/latex] 9{-5}[/latex] C. (a) Какова угловая частота колебаний в цепи? б) Каков максимальный ток, протекающий по цепи? в) Через какое время конденсатор полностью разрядится? (d) Найдите уравнение, которое представляет q(t) .

Стратегия

Угловая частота цепи LC определяется уравнением 14.41. Чтобы найти максимальный ток, максимальная энергия в конденсаторе устанавливается равной максимальной энергии в катушке индуктивности. Время, в течение которого конденсатор разрядится, если он изначально заряжен, составляет четверть периода цикла, поэтому, если мы вычислим период колебаний, мы сможем узнать, какую четверть этого времени нужно найти. {3}t\right).[/latex]

Значение

Соотношение энергий, установленное в части (b), — не единственный способ, которым мы можем приравнять энергии. В большинстве случаев некоторая энергия сохраняется в конденсаторе, а некоторая энергия хранится в катушке индуктивности. Мы можем поместить оба термина в каждую часть уравнения. Исследуя цепь только при отсутствии заряда на конденсаторе или отсутствии тока в катушке индуктивности, мы упрощаем уравнение энергии.

Проверьте свои знания

Угловая частота колебаний в 9{3}[/latex] рад/с. (a) Если [латекс]L=0,10\фантом{\правило{0,2em}{0ex}}\текст{H}[/латекс], что такое C ? (b) Предположим, что при [latex]t=0,[/latex] вся энергия запасается в индукторе. Каково значение [latex]\varphi ?[/latex] (c) Второй идентичный конденсатор подключен параллельно исходному конденсатору. Какова угловая частота этого контура?

Показать раствор

а. [латекс] 2,5 мк\текст {F}[/латекс]; б. [латекс]\pi \text{/}2\phantom{\rule{0. {3} \ фантом {\ правило {0.2em} {0ex} }\text{рад/с}[/латекс]

Резюме

• Энергия, передаваемая колебательным образом между конденсатором и катушкой индуктивности в цепи LC , происходит с угловой частотой [латекс]\омега =\sqrt{\frac{1}{LC}}[/latex] .
• Заряд и ток в цепи задаются как

  [латекс]\begin{array}{ccc}\hfill q\left(t\right)& =\hfill & {q}_{0}\phantom{\rule {0.2em}{0ex}}\text{cos}\left(\omega t+\varphi \right),\hfill \\ \hfill i\left(t\right)& =\hfill & \text{-}\ omega {q}_{0}\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\omega t+\varphi \right).\hfill \end{array}[/latex]

Концептуальные вопросы

Применяются ли правила Кирхгофа к цепям, содержащим катушки индуктивности и конденсаторы?

Показать решение

да

Может ли элемент схемы иметь как емкость, так и индуктивность?

Что в схеме LC определяет частоту и амплитуду колебаний энергии в катушке индуктивности или конденсаторе?

Показать решение

Амплитуда колебаний энергии зависит от начальной энергии системы. Частота в 9Схема 0017 LC зависит от значений индуктивности и емкости.

Проблемы

Конденсатор емкостью 5000 пФ заряжается до 100 В, а затем быстро подключается к катушке индуктивности 80 мГн. Определите (а) максимальную энергию, запасенную в магнитном поле индуктора, (б) пиковое значение тока и (в) частоту колебаний цепи.

Собственная индуктивность и емкость схемы LC составляют 0,20 мГн и 5,0 пФ. С какой угловой частотой колеблется контур? 9{-7}\phantom{\rule{0.2em}{0ex}}\text{s}[/latex]

Собственная индуктивность и емкость колебательного контура LC составляют [латекс] L = 20\phantom{\rule{0.2em}{0ex}}\text{мГн и}\phantom{\rule{0.2em}{ 0ex}}C=1.0\phantom{\rule{0.2em}{0ex}}\mu \text{F},[/latex] соответственно. а) Какова частота колебаний? б) Если максимальная разность потенциалов между пластинами конденсатора равна 50 В, какова максимальная сила тока в цепи?

В качающемся LC , максимальный заряд конденсатора [латекс]{q}_{м}[/латекс]. Определить заряд конденсатора и ток через катушку индуктивности, когда энергия распределяется поровну между электрическим и магнитным полями. Выразите ответ в терминах [латекс]{q}_{m}[/латекс], L и C .

Показать раствор

[латекс]q=\frac{{q}_{m}}{\sqrt{2}},I=\frac{{q}_{m}}{\sqrt{2LC}} [/латекс]

В схеме, показанной ниже, [латекс]{\текст{S}}_{1}[/латекс] одновременно размыкается и [латекс]{\текст{S}}_{2}[/латекс] закрывается. Определить: а) частоту результирующих колебаний, б) максимальный заряд конденсатора, в) максимальный ток через катушку индуктивности, г) электромагнитную энергию колебательного контура. 9{-12}\phantom{\rule{0.2em}{0ex}}\text{F}\hfill \end{массив}[/latex]

Глоссарий

LC схема

Схема

, состоящая из источника переменного тока, катушки индуктивности и конденсатора

.

Лицензии и атрибуты

Колебания в цепи LC. Автор: : Колледж OpenStax.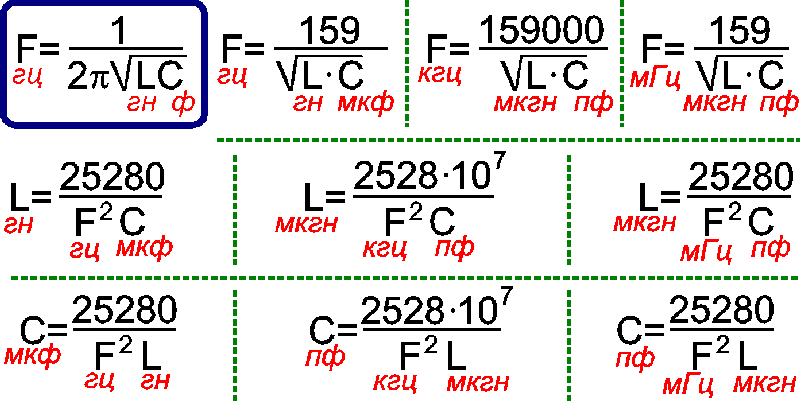 Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/14-5-oscillations-in-an-lc-circuit. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction

Калькулятор резонансной частоты — все RF

Резонансная частота LC-контура – ​​это частота, при которой индуктивное и емкостное сопротивления LC-контура равны.

Этот онлайн-калькулятор резонансной частоты разделен на три калькулятора.

Калькулятор 1: Вычисляет резонансную частоту LC-контура путем ввода значений индуктивности и емкости.

Калькулятор 2: Рассчитывает значение индуктивности LC-контура для заданной частоты и значения емкости.

Калькулятор 3: Рассчитывает значение емкости контура LC Tank для заданной частоты и значения индуктивности.

Калькулятор резонансной частоты

В LC-цепи резонансной частотой называется частота, при которой возникает резонанс, т. е. при этой частоте индуктивное и емкостное сопротивления LC-цепи равны.

Этот онлайн-калькулятор резонансной частоты вычисляет резонансную частоту LC-контура, вводя значение индуктивности (нГн) и емкости (пФ).

Этот онлайн-калькулятор также предоставляет следующие дополнительные калькуляторы:

1. Для расчета индуктивности (нГн) путем ввода значения емкости (пФ) и частоты (ГГц).
2. Чтобы рассчитать емкость (пФ), введите значение индуктивности (нГн) и частоты (ГГц).

Какова резонансная частота LC-контура? Пожалуйста, укажите еще пару моментов для резонансной частоты. Почему это важно, что такое резонансные цепи, как это влияет на цепь

В LC-цепи резонансной частотой называется частота, при которой возникает резонанс, т. е. на этой частоте индуктивное сопротивление и емкостная реактивность LC-цепи равны равный.