Как рассчитать индуктивность катушки различных типов. Какие формулы и методы используются для вычисления параметров катушек индуктивности. Где найти онлайн-калькуляторы для быстрого расчета катушек.
Основные виды катушек индуктивности
Катушки индуктивности являются важнейшими компонентами многих электронных устройств. По конструкции их можно разделить на несколько основных типов:
- Соленоид — цилиндрическая катушка с одним слоем намотки
- Многослойная цилиндрическая катушка
- Тороидальная катушка на магнитном сердечнике
- Плоская спиральная катушка
- Катушка на ферритовом стержне
Расчет индуктивности для каждого типа имеет свои особенности и требует применения специальных формул. Рассмотрим основные методы расчета для наиболее распространенных видов катушек.
Расчет индуктивности соленоида
Соленоид представляет собой простейший вид катушки — цилиндр с одним слоем намотки провода. Для расчета его индуктивности используется следующая формула:
L = (μ0 * N^2 * S) / l
Где:
- L — индуктивность в Генри
- μ0 — магнитная проницаемость вакуума (4π * 10^-7 Гн/м)
- N — число витков
- S — площадь поперечного сечения катушки
- l — длина намотки
Эта формула дает достаточно точный результат для длинных соленоидов, у которых длина намного больше диаметра. Для коротких катушек вводится поправочный коэффициент.
Расчет многослойных цилиндрических катушек
Для катушек с несколькими слоями намотки применяется более сложная формула:
L = (0.8 * N^2 * D^2) / (6D + 9l + 10c)
Где:
- L — индуктивность в микрогенри
- N — общее число витков
- D — средний диаметр катушки в см
- l — длина намотки в см
- c — толщина намотки в см
Эта формула дает погрешность не более 1% для катушек с отношением длины к диаметру от 0.5 до 2.
Особенности расчета тороидальных катушек
Индуктивность тороидальной катушки на магнитном сердечнике рассчитывается по формуле:
L = (μ0 * μ * N^2 * h * ln(D2/D1)) / (2π)
Где:
- μ — относительная магнитная проницаемость сердечника
- h — высота тороида
- D1, D2 — внутренний и внешний диаметры
При расчете важно учитывать нелинейность магнитных свойств сердечника при больших токах и высоких частотах.

Программы и онлайн-калькуляторы для расчета катушек
Для быстрого расчета параметров катушек индуктивности удобно использовать специализированные программы и онлайн-сервисы. Наиболее популярные из них:
- Coil32 — бесплатная программа с широкими возможностями расчета различных типов катушек
- Калькулятор индуктивности на сайте RadioHobby.org
- Онлайн-калькулятор от Electroschematics.com
- Mini Ring Core Calculator для расчета тороидальных катушек
Такие инструменты позволяют быстро рассчитать нужные параметры катушки без сложных вычислений вручную.
Практические рекомендации по намотке катушек
При изготовлении катушек индуктивности своими руками важно учитывать ряд практических моментов:
- Выбирать провод с качественной изоляцией подходящего сечения
- Обеспечивать плотную равномерную намотку витков
- Использовать каркасы из диэлектрических материалов
- Учитывать влияние близко расположенных металлических деталей
- Фиксировать обмотку лаком или клеем для предотвращения саморазмотки
Соблюдение этих рекомендаций позволит изготовить катушку с параметрами, близкими к расчетным.
Измерение индуктивности готовых катушек
После изготовления катушки рекомендуется проверить ее реальную индуктивность. Для этого используются специальные приборы:
- LC-метры
- Измерители RLC
- Анализаторы импеданса
Также можно применять косвенные методы измерения, например, по резонансной частоте контура с известной емкостью. Измерение позволяет скорректировать число витков для получения требуемой индуктивности.
Учет паразитных параметров катушек
При расчете и применении катушек индуктивности важно учитывать их паразитные параметры:
- Активное сопротивление обмотки
- Собственную емкость между витками
- Потери в магнитопроводе (для катушек с сердечником)
Эти факторы влияют на добротность катушки и ее поведение на высоких частотах. Для их минимизации применяют специальные методы намотки и выбор оптимальной геометрии катушки.
Заключение
Расчет катушек индуктивности — важный этап проектирования многих электронных устройств. Правильный выбор конструкции и точный расчет параметров позволяют создать катушку с оптимальными характеристиками для конкретного применения. Использование современных программ и онлайн-калькуляторов значительно упрощает процесс расчета и подбора параметров катушек различных типов.

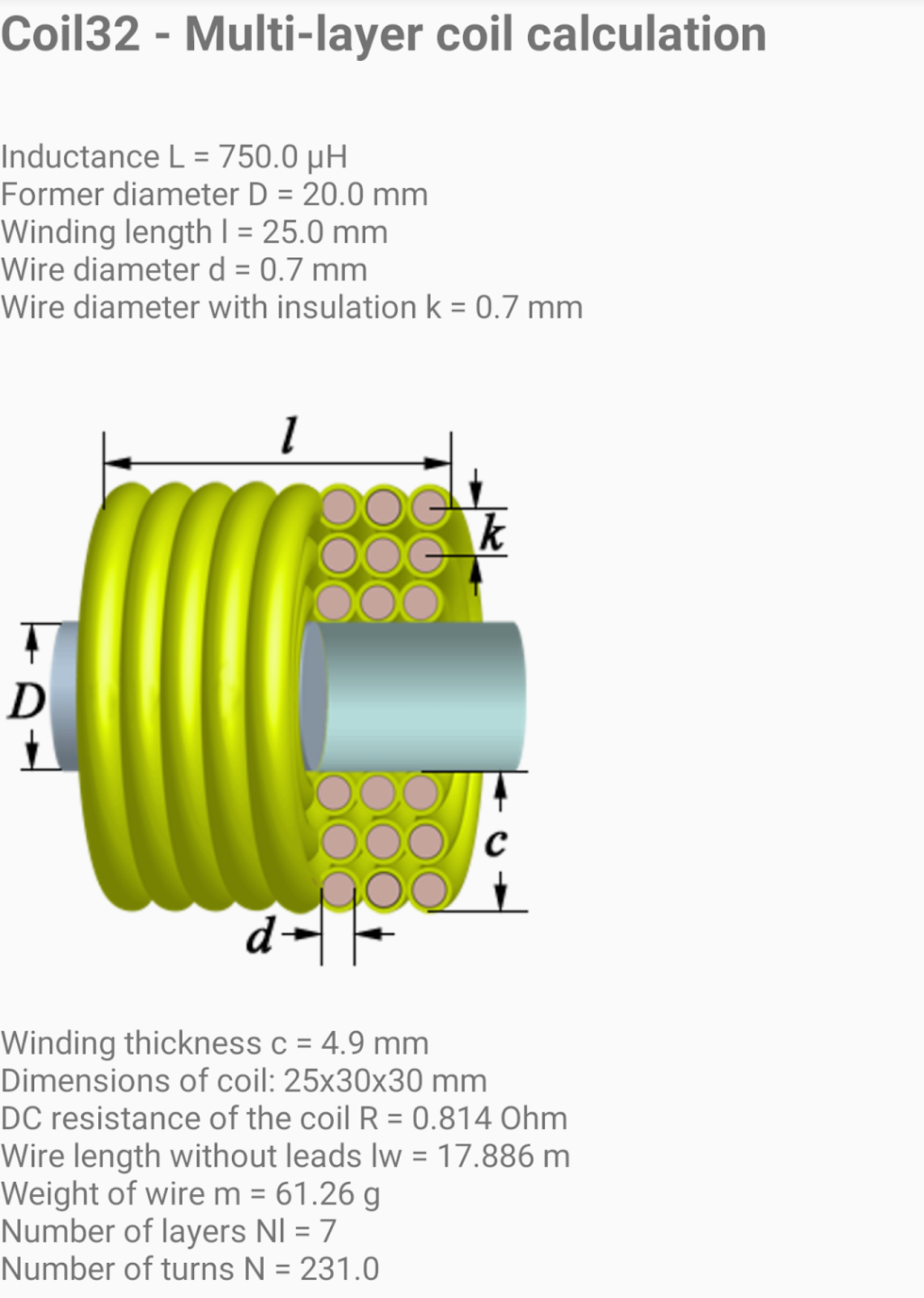
Онлайн калькулятор расчета многослойной катушки индуктивности
На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить – намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.
Для расчета индуктивности многослойной катушки используется такая формула:
Где,
- d – сумма диаметра каркаса и толщины намотки только с одной стороны;
- n – количество витков;
- g – толщина намотанной проволоки;
- h – высота намотанной проволоки;
Из этой формулы, зная величину индуктивности, можно вывести толщину намотки:
Для определения количества витков необходимо воспользоваться формулой:
Где,
- dпр – диаметр провода
- h – высота катушки;
- g – толщина намотки.

Длину одного витка можно определить следующим образом:
lвит = π * dвит
Где π – это константа, а dвит_— это диаметр витка.
Тогда, зная общее число витков и принимая, что d – это усредненное значение диаметра для всех витков, длина всего провода будет определяться по формуле:
Lw
Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.
R = ρ * ( Lw / S ),
где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь проводника, которая определяется по формуле:
Подставив значение площади и длины провода, получим такое выражение для определения сопротивления:
Из значения сопротивления можно вывести формулу для определения диаметра провода, подставив предварительно формулу для вычисления количества витков:
После получения величины диаметра провода, можно определить количество витков, которое подставляется с остальными данными в первую формулу для расчета индуктивности.
Число слоев можно определить, разделив толщину намотки на диаметр провода:
N = g / dпр
Посредством вышеприведенных вычислений можно определить все параметры многослойной катушки индуктивности, которые помогут вам изготовить устройство с нужными параметрами. Также, чтобы облегчить вычисления вы можете воспользоваться нашим онлайн калькулятором ниже.
Собственная паразитная ёмкость катушки индуктивности. Онлайн расчёт.
Собственная ёмкость — это паразитный параметр катушки индуктивности. Паразитный, но не так, чтобы уж очень: не домашнее животное в виде
таракана, не нежданный гость в виде татарина, а так… мелкий, но важный аспект, требующий учёта и внимания.
Возникновение собственной ёмкости обусловлено наличием ёмкостей между отдельными витками катушки, между витками и сердечником, витками
и экраном, а также витками и близлежащими элементами конструкции. Все эти распределённые ёмкости суммируются и называются собственной
ёмкостью катушки CL.
Паразитная собственная ёмкость всегда подключена параллельно катушке и образует с её собственной индуктивностью параллельный колебательный
контур, резонансная частота которого является частотой собственного резонанса катушки.
Несмотря на кажущуюся простоту, точный расчёт этого параметра — это вовсе: не плёвое дело, не поиск халявы и не комариная плешь, по крайней
мере, практически все отечественные авторы справочной литературы, дружно повернулись спиной к суровой правде бытия, выдавая за истину
теорию, никак не подкреплённую экспериментом.
Для примера приведу выдержку из подобного умного справочника.
Совсем другое дело — буржуйские пытливые умы, преимущественно американской этнической национальности. Эти ребята копают и вглубь и вширь похлеще азиатских хунвейбинов, восполняя нехватку теоретических обоснований многочисленными практическими экспериментами.
Вот как, к примеру, у них выглядит незамысловатая измерительная приблуда для определения собственной резонансной частоты катушки.
В результате всех этих раскопок из глубины на поверхность была извлечена совсем уж до неприличия простая формула определения собственной
ёмкости катушки:
Казалось бы, вот оно — добро пожаловать «за грань добра и зла». Однако не всё так плохо — формула обеспечивает вполне приемлемую
точность вычислений и может быть использована для оценки собственных ёмкостей однослойных конструкций катушек с соотношением
длины намотки к диаметру:
0.5 нам/Dкат
А как посчитать нам величину собственной ёмкости при другом форм-факторе катушки?
Найти всеобъемлющую формулу, позволяющую рассчитать этот параметр для любых вариаций (включая частотную зависимость) оказалось делом
нереальным — по крайней мере мне этого сделать не удалось. Поэтому самым простым и точным методом, позволяющим оценить собственную
ёмкость катушки, я посчитал интерполяцию графика экспериментальной зависимости, полученной англичанином R.G.Medhurst-ом, в лаборатории
компании General Electric.
По шкале X — отношение длины к диаметру катушки;
По шкале Y — коэффициент H, равный отношению собственной ёмкости к диаметру катушки;
Шкала зависимости — логарифмическая.
Формула значения собственной ёмкости катушки в данном случае выглядит следующим образом:
CL(пф) = H×Dкат(см).
Зависимость снята для однослойных бескаркасных катушек в диапазоне частот, находящихся ниже частоты собственного резонанса катушки.
В этом же источнике приведена и удобная таблица, отражающая изменение коэффициента H в зависимости от форм-фактора катушки.
И, как результат — формула, позволяющая с 2-3% точностью описать полученные экспериментальные зависимости:
H = 0,1126×L/D+0,08+0,27/√L/D.
Это то, что касается бескаркасных катушек. При наличии гладкого каркаса расчётная ёмкость изделия увеличится на величину ≈10×ε (%), где ε — относительная диэлектрическая проницаемость материала каркаса. Для катушек, намотанных на каркасах с нарезкой для фиксации витков, коэффициент увеличения ёмкости уже может составлять величину ≈20×ε (%).
И в завершении мероприятия просуммируем вышеизложенные идеи калькулятором.
ТАБЛИЦА РАСЧЁТА ЗНАЧЕНИЯ СОБСТВЕННОЙ ЁМКОСТИ БЕСКАРКАСНОЙ КАТУШКИ.
Будьте внимательны — в качестве значения межвиткового расстояния принято считать расстояние между центрами соседних витков, а не зазор между ними, поэтому данное расстояние никак не может быть меньше величины диаметра провода.
Значение собственной ёмкости многослойной катушки значительно больше и может достигать нескольких десятков пФ.
Здесь, помимо всего прочего, вступают в сложное взаимодействие и ёмкости между соседними витками, и ёмкости между слоями, и разные другие
факторы, значительно усложняющие структуру длинной линии, описывающей свойства моточного изделия.
Или я чего-то пропустил в этой жизни…
Расчёт индуктивности. Часть 2 | HomeElectronics
Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Виды катушек индуктивности
Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности
Расчёт индуктивности катушки.
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:
D1 – внутренний диаметр, D2 – внешний диаметр, Dср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:
если l > Dср – длинная катушка,
если l < Dср – короткая катушка,
если l << Dср – очень короткая катушка,
если l = 0 – плоская катушка,
если t ≈ Dср – толстая катушка,
если t << Dср – тонкая катушка,
если t = 0 – соленоид.
Особенности расчёта катушек индуктивности
Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением
где LР – расчётная индуктивность;
∆L – поправка на «изоляцию», ∆L = ∆1L + ∆2L;
∆1L – поправка учитывающая влияние индуктивности витков;
∆2L – поправка учитывающая влияние взаимной индуктивности витков.
В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности LР, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.
Особенности расчёта круговых катушек индуктивности состоят в следующем:
1. При определении расчётной индуктивности LP, средний диаметр принимается равным среднему диаметру реальной катушки;
2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении
3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.
4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.
5. Так как величина поправки на взаимную индуктивность ∆2L в несколько раз меньше, чем поправка на индуктивность витков ∆1L, то при расчётах можно учитывать только ∆1L.
Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.
Расчёт индуктивности соленоида
Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.
Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
d – диаметр соленоида, м;
Φ – коэффициент, который зависит от отношения α = l/D;
l – длина соленоида, м;
Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d
Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит
Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит
Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.
Индуктивность плоской катушки
Определение индуктивности плоской катушки, D1 – внутренний диаметр, D2 – внешний диаметр, D – средний диаметр, t – толщина намотки.
В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
D – средний диаметр катушки, м;
Ψ – коэффициент, который зависит от отношения ρ = t/D;
t – толщина намотки катушки.
Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D
При небольшой толщине намотки, когда ρ < 0,5
При большой толщине намотки, когда ρ > 0,5
где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки
Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.
Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.
Индуктивность круговой катушки прямоугольного сечения
Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник
Индуктивность прямоугольной катушки.
Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.
Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле
где L0 – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/Dcp;
l – длина катушки, м;
Dcp – средний диаметр катушки, м;
∆ — поправка на форму катушки.
В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру Dcp, можно разделить на несколько типов:
1. Длинная катушка, у которой α > 0,75.
2. Короткая катушка, имеющая α < 0,75 и γ < 1.
3. Очень короткая катушка, имеет α << 1 и γ > 1.
где
Рассмотрим каждый случай по отдельности.
Индуктивность длинной катушки
Длинная катушка.
Для длинной катушки (α > 0,75) величина L0 рассчитывается также как для длинного соленоида, где l – длина соленоида, Dcp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
где D1 – внутренний диаметр, D2 – внешний диаметр.
Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром DCP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.
Индуктивность короткой катушки
Короткая катушка.
Для короткой катушки (α < 0,75, t < l) величина L0 рассчитывается также как для короткого соленоида, где l – длина соленоида, DСР – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром DСР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.
Индуктивность очень короткой катушки
Очень короткая катушка.
Для очень короткой катушки (α << 1, t > l) величина L0 рассчитывается также как для плоской катушки, где t – толщина намотки, Dcp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром DCP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.
Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).
Расчёт поправки на взаимную индуктивность витков
В общем случае поправка на взаимную индуктивность витков ∆2L катушки определяется выражением
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
J – коэффициент, зависящий формы катушки и от числа витков катушки.
1. Для катушки выполненной в один слой по длине катушки (соленоид):
а) при определении расчётной индуктивности LP толщина намотки t принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит
где ω – количество витков катушки.
2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):
а) при определении расчётной индуктивности LP длина катушки l принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит
где ω – количество витков катушки.
На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Бесплатная программа расчёта катушек индуктивности Coil32 — Софт для радиолюбителя — Программы
Катушки индуктивности практически используются почти в любой радио-аппаратуре, и довольно часто перед радиолюбителями возникает вопрос:
Как рассчитать индуктивность той, или иной катушки? Конечно можно рассчитать индуктивность по определённым формулам, но это требует времени, которого радиолюбителям всегда не хватает.
Бесплатная программа Coil32, автором которой является Кустарев Валерий, позволяет быстро рассчитать индуктивность практически любой катушки.
В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки, так же можно сразу рассчитать и ёмкость конденсатора в колебательном контуре.
Программа бесплатна и свободна для использования и распространения. В последней версии Coil32 v11.6.1.890 доступны расчёты:
- Одиночный круглый виток
- Однослойная виток к витку
В качестве начальных параметров при расчете катушки можно выбрать два варианта:- Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
- Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
- Однослойная катушка с шагом
- Катушка с не круглой формой витков
- Многослойная катушка
В качестве начальных параметров при расчете катушки можно выбрать два варианта:- Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки («сколько надо отрезать»).
- Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода и приблизительная длина провода для намотки.
- Тороидальная однослойная катушка
- Катушка на ферритовом кольце
- Катушка в броневом сердечнике
(Ферритовом и карбонильном) - Тонкопленочная катушка
(Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)
В чем преимущества данной программы перед аналогами?
- Программа рассчитывает индуктивность различных типов катушек под имеющийся каркас.
- Результаты расчетов выводятся в текстовое поле справа, откуда их можно сохранить в файл. Можно открыть этот файл в «MS Word» и распечатать.
- Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
- Можно рассчитать основные параметры колебательного контура для однослойной катушки
- Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце.
- Для расчёта катушек в броневых сердечниках, есть возможность выбора одного из нескольких стандартных сердечников, что позволяет рассчитать катушку в несколько кликов.
- Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
- Программа имеет мультиязычный интерфейс (20 языков) и дополнительные наборы скинов, которые можно скачать и установить из меню «Настройки».
Программа распространяется бесплатно в стиле «Portable» и не имеет установщика. Для работы с программой — скачайте архив, распакуйте его в любое удобное для Вас место и запустите файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.
Скачать Coil32.
расчет катушки на ферритовом стержне
Программа позволяет производить расчет следующих типов катушек индуктивности:
- Одиночный круглый виток
-
Однослойная виток к виткуВ качестве начальных параметров при расчете катушки можно выбрать два варианта:
- Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
- Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
- Однослойная катушка с шагом
- Катушка с не круглой формой витков
-
Многослойная катушка В качестве начальных параметров при расчете катушки можно выбрать два варианта:
- Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки («сколько надо отрезать»).
- Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода и приблизительная длина провода для намотки.
- Тороидальная однослойная катушка
- Катушка на ферритовом кольце
- Катушка в броневом сердечнике(Ферритовом и карбонильном)
- Тонкопленочная катушка(Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)
Подробнее о Coil32 …
Довольно часто перед радиолюбителем встает вопрос: » Как рассчитать индуктивность катушки?». Катушки используются и в высокочастотной связной аппаратуре, и при конструировании акустических систем, и даже взглянув на материнскую плату компьютера, Вы и там обнаружите индуктивные элементы. С помощью программы Coil32 можно быстро рассчитать индуктивность катушки. В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки можно «не отходя от кассы» рассчитать емкость конденсатора в колебательном контуре.
В чем преимущества программы перед аналогами?
- Программа рассчитывает индуктивность многих типов катушек. Можно подобрать оптимальный вариант, либо пересчитать катушку под имеющийся каркас.
- Результаты всех расчетов выводятся в текстовое поле, откуда их можно сохранить в файл. В дальнейшем Вы можете их просмотреть, чтобы не пересчитывать заново. Можно открыть этот файл в «MS Word» и распечатать.
- Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
- Рассчитываются основные параметры колебательного контура для однослойной катушки
- Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце
- Для катушек в броневых сердечниках есть возможность выбрать один из нескольких стандартных, что позволяет рассчитать катушку несколькими щелчками мыши.
- Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
- В Сети часто встречаются программы для расчета индуктивности, работающие под DOS, о преимуществах Windows-интерфейса, думаю, говорить не приходится.
- Программа имеет возможность расширения функционала с помощью дополнительных плагинов для расчета индуктивностей
- Программа имеет мультиязычный интерфейс и скины, дополнительные наборы скинов можно найти на .
Программа распространяется в стиле «Portable» и не имеет установщика. Для установки программы распакуйте архив программы в любой каталог и запустите на выполнение файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.
Калькулятор взаимной индукции
Этот калькулятор определяет взаимоиндукцию двух связанных катушек индуктивности.
Пример. Рассчитать взаимную индуктивность двух расположенных рядом катушек индуктивности 10 мкГн и 5 мкГн с коэффициентом связи 0,5.
Входные данные
Индуктивность первой катушки, L1
генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)
Индуктивность второй катушки, L2
миллигенри (мГн)
Коэффициент связи, k
0 ≤ k ≤ 1
Выходные данные
Взаимоиндукция
M миллигенри (мГн)
Введите величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать.
В токоизмерительных клещах с разъемным магнитопроводом для безопасного измерения тока без необходимости подключать прибор к схеме используется измерительный трансформатор. В приборе используется явление взаимной индукции. На разъемном магнитопроводе надета катушка, являющаяся вторичной обмоткой измерительного трансформатора. Первичной «обмоткой» является охватываемый магнитопроводом провод с током. Электродвижущая сила, возникающая в катушке на магнитопроводе, пропорциональна току, текущему в проводнике, охваченном клещами. Прибор измеряет напряжение на зажимах катушки и указывает на дисплее значение измеряемого тока.
Калькулятор определит взаимоиндукцию M двух связанных катушек индуктивности по формуле:
где k — коэффициент связи, L₁ — индуктивность первой катушки и L₂ — индуктивность второй катушки. Коэффициент связи определяется как отношение взаимоиндукции двух катушек к максимально возможному значению их взаимоиндукции. Коэффициент связи изменяется в пределах от 0 до 1 и зависит от близости катушек или обмоток, материала их сердечника, их взаимной ориентации, формы и количества витков. У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.
Тороидальные трансформатор и дроссель в импульсном блоке питания
Пример расчетов. Коэффициент связи двух катушек с индуктивностью 2 мкГн и 3 мкГн равен 0,5. Взаимоиндукция в микрогенри определяется как
Две катушки с взаимной индукцией на принципиальной схеме
При увеличении электрического тока, протекающего через катушку индуктивности L₁ от внешней цепи, вокруг катушки создается увеличивающееся магнитное поле, в котором сохраняется энергия. При уменьшении тока магнитное поле также уменьшается. При этом на выводах катушки возникает напряжение (ЭДС самоиндукции) в направлении, противоположном направлению тока, и сохраняемая в магнитном поле энергия отдается обратно во внешнюю цепь. Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).
Взаимоиндукция в вашем автомобиле: для создания искры в свечах зажигания используется катушка зажигания, представляющая собой трансформатор с высоким коэффициентом трансформации. Когда ток через первичную обмотку с малым числом витков прерывается, очень большая ЭДС возникает во вторичной обмотке с большим числом витков, которая достаточна для создания искры в зазоре автомобильной свечи зажигания
В обратной ситуации, если ток течет в катушке L₂, а наводится ток в катушке L₁, взаимоиндукция будет той же. Отметим, что электродвижущая сила (ЭДС) возникает только при изменении тока, причем чем быстрее изменяется ток, тем больше будет ЭДС. То есть, ЭДС взаимной индукции прямо пропорциональна скорости изменения тока
Явление взаимной индукции используется в трансформаторах, электродвигателях, генераторах и других устройствах, в которых для функционирования необходимо взаимодействие с магнитным полем. В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.
Расчет катушек на кольцах Amidon из порошкового железа:
Ферритовые кольца фирмы Amidon не имеют цветовой маркировки (блестящие черные либо тускло-серые), Здесь калькулятор для их расчета. Изделия из порошкового железа (карбонильного) маркируются цветом в зависимости от материала кольца. – здесь полный набор характеристик. Расчет ведется по формуле:
ВЫБЕРИТЕ КОЛЬЦО:
| Тип материала кольца – | 123678101215171826304052 |
| Типоразмер кольца – | T-5T-10T-12T-16T-20T-25T-30T-37T-44T-50T-68T-80T-94T-106T-130 |
Доступная информация о кольце:
Цветовой код: Материал: Рабочие частоты LC цепей Начальная магнитная проницаемость (μ): Размеры (OD x ID x H): дюймммAL фактор: мкГн/(N/100)2ВВЕДИТЕ ИСХОДНЫЕ ДАННЫЕ:
| L | = мГнмкГннГн | – Требуемая индуктивность |
Рассчитать
Результат:
| N | = | – Число витков |
МАТЕРИАЛ №0: В основном используется на частотах выше 100 МГц. Индуктивность (или число витков), полученная из расчетов, исходя из заданного параметра AL, не может быть достаточно точной и сильно зависит от техники намотки.МАТЕРИАЛ №1: Очень похож на материал №3 за исключением более высокого объемного сопротивления и повышенной стабильности.МАТЕРИАЛ №2: Carbonyl ‘E’ порошковый материал с высоким объемным сопротивлением. Для изготовления высокодобротных катушек на частотах от 2 МГц до 20 МГц.МАТЕРИАЛ №3: Carbonyl ‘HP’ материал с прекрасной стабильностью и добротностью для низких частот от 50 КГц до 500 КГц.МАТЕРИАЛ №6: Carbonyl ‘SF’ материал. Предназначен для катушек с высокой добротностью и температурной стабильностью для частот 20 МГц — 50 МГц.МАТЕРИАЛ №7: Carbonyl ‘TH’ материал. Очень похож на №2 и №6, но имеет более высокую температурную стабильность.МАТЕРИАЛ №8: Этот материал имеет низкие потери в сердечнике и хорошую линейность в условиях высокого смещения по кривой намагничивания. Хороший высокочастотный материал. Самый дорогой материал.МАТЕРИАЛ №10: Порошковый материал «W». Обеспечивает хорошую добротность и высокую стабильность для частот от 40 МГц до 100 МГц.МАТЕРИАЛ №12: Синтетический оксидный материал, который обеспечивает хорошую добротность и умеренную стабильность для частот от 50 МГц до 200 МГц. Если высокое значение Q имеет первостепенное значение, этот материал является хорошим выбором. Если первостепенное значение имеет стабильность, предпочтительным будет материал № 17.МАТЕРИАЛ №15: Карбонильный материал «GS6». Обладает отличной стабильностью и хорошей добротностью. Хороший выбор для коммерческих частот вещания, где важны «Q» и стабильность.МАТЕРИАЛ №17: Это новый карбонильный материал, который очень похож на материал № 12, но он обладает лучшей температурной стабильностью. Однако по сравнению с материалом № 12 наблюдается небольшая потеря добротности, составляющая около 10% в диапазоне от 50 МГц до 100 МГц. На частотах выше 100 МГц добротность хуже примерно на 20%.МАТЕРИАЛ №18: Этот материал имеет низкие потери в сердечнике, аналогично материалу № 8, но с более высокой проницаемостью и более низкой стоимостью. Хорошие характеристики насыщения при постоянном токе.МАТЕРИАЛ №26: Материал с пониженным содержанием водорода. Обладает наивысшей проницаемостью из всех порошковых материалов. Используется для фильтров электромагнитных помех и дросселей постоянного тока.МАТЕРИАЛ №30: Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №40: Недорогой материал. Имеет характеристики, похожие на очень популярный материал № 26. Хорошая линейность, низкая стоимость и относительно низкая проницаемость этого материала делают его популярным для мощных дросселей ИБП больших размеров.МАТЕРИАЛ №52: Этот материал имеет более низкие потери в сердечнике при высокой частоте и такую же проницаемость, что и материал № 26. Популярен для новых конструкций высокочастотных дросселей.
Ссылки по теме:
Виды катушек индуктивности
Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:
D1 – внутренний диаметр, D2 – внешний диаметр, Dср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:
если l > Dср – длинная катушка,
если l ср – короткая катушка,
если l ср – очень короткая катушка,
если l = 0 – плоская катушка,
если t ≈ Dср – толстая катушка,
если t ср – тонкая катушка,
если t = 0 – соленоид.
Индуктивность кругового кольца круглого сечения
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид
При этом его индуктивность можно вычислить по следующему выражению
для постоянного тока
где R – радиус витка, м, R = D/2;
r – радиус провода, м, r = d/2;
μ – магнитная постоянная, μ = 4π•10-7 Гн/м.
Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.
Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).
Для постоянного тока индуктивность составит
На частоте 50 кГц
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
где μ – магнитная постоянная, μ = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).
Эквивалентная схема реальной катушки индуктивности
В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.
Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.
Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками
Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.
Катушки индуктивности и обмотки в различных устройствах
Конструктивный расчет многослойной катушки индуктивности (индуктивность — 80 мкГн, частота — 0,25 МГц, форма экрана
Министерство образования и науки
Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра конструирования и технологии радиоэлектронных средств
Расчетно-графическое задание по дисциплине
«Радиоматериалы и радиокомпоненты»
на тему «Конструктивный расчет многослойной катушки индуктивности»
Вариант №10
Выполнил: Проверил: Плавский Л. Г.
|
Оценка |
||
|
Выполнение |
Защита |
Общая |
Студент: Торчевский А.А.
Группа: РТ5-91
Новосибирск 2010
|
Индуктивность, мкГн |
Частота, МГц |
Форма экрана |
Вариант расположения выводов |
|
80 |
0.25 |
Круглый |
— |
Расчеты:
Расчет геометрических параметров и индуктивности
Для многослойных катушек справедливы следующие соотношения:
где D – внешний диаметр; – внутренний диаметр; t – радиальная толщина обмотки; l – длина.
Возьмем D0=12мм, а l=5мм:
тогда
;
ОтсюдаD=16мм.
Имеем многослойную катушку с параметрами:
D=16 мм, =12 мм, l=5 мм, t=2 мм.
Обычно для многослойных катушек берут следующее соотношение между диаметром экрана и диаметром катушки:
[2].
Также должно выполняться соотношение
Отсюда при диаметр экрана =25.6 мм.
Длина экрана .
Индуктивность катушки без экрана можно найти по формуле:
[1, ф.4-59]
Где – коэффициент связи, – заданное значение индуктивности.
Коэффициент связи катушки с экраном kможно определить из выражения:
; [1, ф.4-61]
где:
приведенный диаметр катушки ;
коэффициенты и находим из соответствующих графиков
[1, рис. 4-8, 4-6; 2, рис. 7.6].
Для определения и необходимы величины:
Dср = = = 14 мм
Из графиков находим: =11, =13.
Коэффициент связи равен:
=0,01575
Отсюда
Число витков [1, ф.4-21]
Оптимальный диаметр провода определяем по формуле
определяется по графику [1, рис. 4-16]. Для его определения нам нужен вспомогательный параметр ψ:
,[1, ф.4-38]
где
K- коэффициент, определяемый по графику [1, рис.4-14]. В данном случае К=14.
Находим ψ:
Находим по графику [1, рис. 4-16]
Определяем оптимальный диаметр
Выбираем провод марки ПЭЛ. Диаметр провода с изоляцией ,
[1, табл.П6]
Угол отклонения [1, ф.4-8], при числе переходов pравным 2. Для провода марки ПЭЛ предельный угол Полученное значение удовлетворяет этим условиям.
Угловой шаг [1, ф.4-3].
Число циклов . Знак «минус», так как предположили намотку с опережением. Находим
Радиальная глубина намотки равна
Полученная глубина намотки отличается от изначально заданной, поэтому отыщем индуктивность катушки при заданных размерах. Фактические диаметры:
;
Ищем фактический коэффициент L0по графику [1, рис. 4-8]. Он равен 11.
Рассчитаем с новыми данными:
[2, ф.7.15]
Полученное значение отличается от заданного на 3,46%.Определим требуемое число витков:
Расчет собственной ёмкости, сопротивления, и добротности
Собственная ёмкость катушки вычисляем по эмпирической формуле: [1, ф.2-28а]
Для ПЭЛ [1,стр.228]
Экран увеличивает собственную ёмкость катушки на 30 — 40%, поэтому собственная ёмкость катушки
Экран вызывает изменение сопротивления катушки, т. е вносит некоторое сопротивление и ослабляет эффект близости. Пусть материалом экрана будет алюминий, тогда вносимое сопротивление рассчитываем по формуле:
[1, ф.4-63]
Толщину экрана зададим исходя из данных [1, стр. 255]. Исходя из частоты, выбираем h=0.3 мм.
Сопротивление постоянному току цилиндрической катушки с зигзагообразной намоткой равно:
[1, ф.4-36]
Сопротивление катушки току высокой частоты без учёта вносимого сопротивления равно:
, [1, ф.4-64]
F (z), G (z) выражаются через функции Бесселя и для медного провода определяются [1, табл.4-5]
z=0.106
F(z)=1,042 G(z)
Общее сопротивление .
Добротность экранированной катушки
Выбор материала
В качестве используемого материала для изготовления каркаса для катушки используем полистирол, так как этот материал экономически более выгоден и прост в изготовлении. На технические параметры многослойных катушек, материал каркаса, как правило, влияния не оказывает [4, стр.167].
Вывод:
При выполнении данного расчетно – графического задания были получены навыки, необходимые при разработке таких элементов радиоэлектронной аппаратуры, как катушки индуктивности.
Литература
1. Волгов В. А Детали и узлы радиоэлектронной аппаратуры. М.: Высшая школа,1975 г.
2. Фрумкин Г. Д. Расчет и конструирование радиоэлектронной аппаратуры. М.: Высшая школа,1985 г.
3. Немцов М. В. Справочник по расчету параметров катушек индуктивности. М.: Энергоатомиздат, 1989 г.
4. Фролов А.Д Радиодетали и узлы. М.: Высшая школа,1975 г
Расчет магнитных параметров катушки индуктивности Практическая работа
Расчет магнитных параметров катушки индуктивности Практическая работа
Расчет магнитных параметров катушки индуктивности Магнитная проницаемость – отношение результирующей индукции магнитного поля в веществе B к индукции B 0 намагничивающего поля. Магнитная проницаемость – физическая величина, характеризующая магнитные свойства вещества, использованного для сердечника. Магнитная проницаемость = величина безразмерная
Расчет магнитных параметров катушки индуктивности S – площадь поперечного сечения соленоида l – длина соленоида
Расчет магнитных параметров катушки индуктивности Наличие железного сердечника внутри соленоида позволяет значительно увеличить начальное значение магнитного потока Магнитный поток будет тем больше, чем большая часть соленоида заполняется железом. Максимальное увеличение = весь соленоид заполнен железом, то есть когда обмотка плотно навита на железный сердечник. Наличие железного сердечника = значительное увеличение магнитного потока, иногда в тысячи раз.
Расчет магнитных параметров катушки индуктивности Увеличение магнитного потока сквозь соленоид при введении в него сердечника = магнитный поток, создаваемое током в обмотке соленоида + магнитный поток, создаваемый совокупностью ориентированных амперовых токов.
Расчет магнитных параметров катушки индуктивности Сердечники из других материалов = изменение магнитного потока Наиболее заметный эффект – материалы, подобные по своим свойствам железу: никель, кобальт и др. При введении в катушку дают увеличение магнитного потока. Это ферромагнитные материалы = ферромагнетики. Магнитная проницаемость = большая: никель = 50, кобальт = 100. Остальные материалы (немагнитные) — оказывают меньшее влияние на магнитный поток, чем ферромагнитные. Изменение магнитного потока можно обнаружить только с помощью тщательных измерений. Магнитная проницаемость μ — маленькая, отлична от единицы, но мало. У одних веществ она больше единицы μ >1 (ПАРАМАГНЕТИКИ) – заполнение ими катушки увеличивает магнитный поток , У других – меньше единицы (ДИАМАГНЕТИКИ) μ
Расчет магнитных параметров катушки индуктивности ПАРАМАГНЕТИКИ УВЕЛИЧИВАЮТ МАГНИТНЫЙ ПОТОК КАТУШКИ ДИАМАГНЕТИКИ УМЕНЬШАЮТ МАГНИТНЫЙ ПОТОК КАТУШКИ
Практическая работа Расчет магнитных параметров катушки индуктивности
Расчет магнитных параметров катушки индуктивности № μ S, м. кв ι, м I, А 1 1, 000014 0, 25 0, 01 0, 1 2 1, 000023 0, 25 0, 01 0, 15 3 1, 000175 0, 25 0, 01 0, 2 4 1, 000253 0, 25 0, 01 0, 25 5 0, 999987 0, 25 0, 01 0, 3 6 0, 999991 0, 25 0, 01 0, 35 7 0, 999963 0, 25 0, 01 0, 4 ω Ф, Вб В, Тл Н, А/м L, Гн Ψ, Гн/А
Расчет магнитных параметров катушки индуктивности № μ 1 1, 000014 2 S, м. кв ι, м I, А 0, 5 0, 15 0, 45 1, 000023 0, 5 0, 15 0, 5 3 1, 000175 0, 15 0, 55 4 1, 000253 0, 5 0, 15 0, 6 5 0, 999987 0, 5 0, 15 0, 65 6 0, 999991 0, 5 0, 15 0, 7 7 0, 999963 0, 5 0, 15 0, 75 ω Ф, Вб В, Тл Н, А/м L, Гн Ψ, Гн/А
Расчет магнитных параметров катушки индуктивности МАГНИТНАЯ ПОСТОЯННАЯ
Расчет магнитных параметров катушки индуктивности ХОД РАБОТЫ
Расчет магнитных параметров катушки индуктивности Зарисовать таблицу с данными
Расчет магнитных параметров катушки индуктивности Рассчитать магнитный поток по формуле:
Расчет магнитных параметров катушки индуктивности Рассчитать магнитную индукцию по формуле:
Расчет магнитных параметров катушки индуктивности Определить напряженность магнитного поля по формуле:
Расчет магнитных параметров катушки индуктивности Определить индуктивность сердечника по формуле:
Расчет магнитных параметров катушки индуктивности Рассчитать потокосцепление самоиндукции по формуле:
Расчет магнитных параметров катушки индуктивности Ответить на контрольные вопросы: 1. Что такое μ и от чего зависит? 2. Дать определение магнитного потока, написать от чего он зависит. 3. Дать определение индукции магнитного поля, написать от чего зависит. 4. Дать определение напряженности магнитного поля, написать от чего зависит. 5. Дать определение индуктивности, написать от чего зависит.
Что такое индуктор — его работа, параметры, факторы и применение
Индуктор и его работа, параметры, факторы и применение
Катушка индуктивности — один из наиболее часто используемых электрических компонентов в цепи. Его называют дросселем, змеевиком или реактором.
Индуктор:
Индуктор — это пассивный электрический компонент с двумя выводами, который накапливает энергию в магнитном поле . Это магнитное поле создается за счет протекания через него тока.
Он в основном состоит из катушки, окружающей сердечник. Каждая катушка по сути является индуктором. Изменение тока через катушку создает вокруг нее магнитное поле. Это магнитное поле, согласно закону Ленца , индуцирует ЭДС на катушке, противоположную направлению входного тока. Таким образом, индуктор препятствует любому изменению тока питания.
Индуктивность:
Индуктивность — это способность или свойство индуктора создавать электродвижущую силу (ЭДС или напряжение) из-за изменения электрического тока.
Это отношение напряжения к скорости изменения тока через катушку индуктивности.
L = V / (di / dt)
Единицей индуктивности СИ является Генри , названная в честь американского ученого Джозефа Генри. Его эквивалент — Вебер / Ампер.
1 Генри — это величина индуктивности, когда изменение тока в катушке на 1 ампер в секунду создает ЭДС в 1 вольт. Он обозначается как H.
Индуктивность катушки индуктивности зависит от многих факторов, которые вкратце обсуждаются ниже.Индукторы обычно имеют индуктивность от 1 мкГн до 20Гн.
Обозначение индуктора:
Существуют различные типы индукторов. На схеме они обозначены различными символами. Обозначения некоторых индукторов приведены ниже:
Работа индуктора:
Согласно правилу электромагнетизма, закон Эрстеда , когда постоянный ток проходит через прямой проводник, он создает вокруг него магнитное поле. Сила магнитного поля зависит от тока питания.Если ток через проводник изменить, результирующее магнитное поле также изменится. Создаваемое магнитное поле перпендикулярно проводнику.
Направление создаваемого магнитного поля можно определить с помощью правила для правой руки Флеминга или правила для правой руки. Согните палец, как будто держите проводник, и направьте большой палец в сторону тока. Большой палец показывает направление тока, в то время как фигурные пальцы показывают направление магнитного поля вокруг проводника.
Как известно, индуктор — это проводник, обернутый в виде катушки. Изменяющееся магнитное поле создается путем изменения тока, проходящего через него. Изменяющееся магнитное поле заставляет магнитные линии пересекать часть проводника, что индуцирует ЭДС в проводах. Это явление известно как самоиндукция.
Согласно Ленцу, эта ЭДС, индуцированная в катушке, противоположна по направлению току питания и препятствует любому изменению тока питания. Чем выше скорость изменения тока питания, тем выше скорость изменения магнитного поля и сильнее противодействующий индуцированный ток.
Проще говоря, реактивное сопротивление (сопротивление) индуктора увеличивается с увеличением частоты питающей сети. Он увеличивается до такой степени, что полностью блокирует входной ток. Таким образом, катушка индуктивности блокирует переменный ток, в то время как она ведет себя как замыкающая цепь для постоянного тока.
Параметры индуктора:
Параметры любого электронного компонента определяют его производительность и использование. Это дает нам представление о том, как и в какой схеме следует использовать эти компоненты.Некоторые параметры индуктора приведены ниже:
Сопротивление постоянному току (DCR):
Сопротивление индуктора для постоянного тока называется сопротивлением постоянному току.
В идеале, индуктор не должен иметь сопротивления постоянному току (DCR), но имеет тенденцию иметь некоторое сопротивление на уровне сигналов 0 Гц или около него. В схеме это моделируется как отдельное последовательное сопротивление с индуктором.
Чтобы измерить сопротивление катушки индуктивности постоянному току, подайте постоянное напряжение и измерьте ток через него. Затем рассчитайте сопротивление, используя закон Ома для заданных напряжения и тока.
R DC = V / I
Обычно это около нескольких Ом. Сопротивление индуктивности постоянному току зависит от длины и площади поперечного сечения используемого провода. Он ниже для катушек индуктивности с низкой стоимостью и выше для катушек с высокой номинальной мощностью.
Ток насыщения:
По сути, увеличение тока через катушку, намотанную вокруг ферромагнитного сердечника, увеличивает поток, создаваемый в нем. В определенный момент сердечник полностью насыщается, и увеличение тока не приводит к увеличению потока в сердечнике.Таким образом, ток, при котором сердечник становится насыщенным, известен как ток насыщения катушки индуктивности.
Превышение тока насыщения снижает проницаемость сердечника. Это впоследствии приводит к резкому снижению индуктивности катушки индуктивности. Снижение индуктивности при токе насыщения составляет от 10 до 20%.
Помните, что только ферромагнитные материалы могут иметь внутри магнитный поток. Таким образом, индуктор с воздушным сердечником не имеет тока насыщения.
Номинальный ток:
Это максимальный номинальный ток, который провод, используемый в обмотке индуктора, может выдерживать при определенной температуре.Индуктор может безопасно работать при этом номинальном токе без повреждения обмотки.
Превышение номинального тока индуктора приведет к термическому повреждению изоляции обмоток, вызывая короткое замыкание витков (что в конечном итоге приведет к разрушению всего устройства).
Установившийся ток через индуктор не должен превышать номинальный ток индуктора.
Проницаемость сердечника:
Проницаемость сердечника играет жизненно важную роль в индуктивности катушки индуктивности.Увеличение проницаемости сердечника увеличивает индуктивность. Размер, форма и материал сердечника влияют на индуктивность.
Собственная емкость:
Как мы знаем, в катушке индуктора есть несколько витков. Между каждым из этих витков есть емкость, потому что витки находятся в непосредственной близости и имеют другой потенциал (только в переменном токе, потому что в постоянном токе обмотка короткая).
При увеличении частоты увеличивается индуктивное реактивное сопротивление и уменьшается емкостное реактивное сопротивление.Благодаря чему катушка индуктивности работает как конденсатор.
Для уменьшения собственной емкости витки обмотки высокочастотных катушек индуктивности расположены далеко друг от друга.
Саморезонансная частота:
Как мы установили, между витками катушки есть емкость. Эта емкость создает параллельную LC-цепь.
При увеличении частоты наступает момент, когда индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению. Эта частота известна как резонансная частота.
Катушка индуктивности имеет очень высокий импеданс на резонансной частоте и выглядит как разомкнутая цепь.
Увеличение частоты выше резонансной приведет к уменьшению емкостного реактивного сопротивления, и катушка индуктивности начнет вести себя как конденсатор. Чтобы избежать этой проблемы, индукторы используются ниже их собственной резонансной частоты.
Потери мощности в индукторе:
Потери в меди
Потери, возникающие из-за сопротивления обмотки индуктора, называются потерями в меди.Эти потери зависят от тока, протекающего через катушку индуктивности.
Потери в меди = I 2 R
Гистерезисные потери
Потери мощности из-за реверсивного магнитного поля в сердечнике называются гистерезисными потерями.
Во время положительного полупериода сердечник намагничивается и насыщается. Во время отрицательного полупериода сердечник не размагничивается немедленно, а тратит часть энергии в сердечнике.
Различные материалы сердечника имеют разные коэффициенты гистерезиса.Материалы с низким коэффициентом гистерезиса имеют низкие гистерезисные потери.
Потери на вихревые токи
Ток, индуцированный в сердечнике индуктора из-за окружающего его магнитного поля, называется вихревым током. Потери из-за этого тока называются потерями на вихревые токи.
Эти потери можно минимизировать, используя ламинированный сердечник.
Факторы, влияющие на индуктивность индуктора:
Индуктивность — это результат действия магнитного поля из-за силы тока на виток в катушке.Есть 4 основных фактора, которые влияют на индуктивность катушки индуктивности. Каждый из них подробно описан ниже;
Длина катушки:
Предположим, что все остальные факторы остаются неизменными, увеличение длины катушки уменьшает индуктивность катушки индуктивности.
Из-за увеличения длины катушки появляется большее сопротивление магнитному полю, создаваемому током на оборот.
Площадь поперечного сечения катушки
Если все остальные факторы остаются неизменными, увеличение площади поперечного сечения катушки увеличивает индуктивность катушки индуктивности.
Из-за увеличения площади поперечного сечения создается меньшее сопротивление создаваемому магнитному полю.
Число витков
Магнитное поле создается за счет протекания тока в этих витках, поэтому увеличение числа витков увеличивает общее магнитное поле. Таким образом увеличивается индуктивность катушки.
Проницаемость сердечника:
Проницаемость сердечника увеличивает магнитное поле катушки в сотни раз.Таким образом, наличие сердечника с высокой магнитной проницаемостью увеличивает индуктивность той же катушки.
Типы индукторов
Вот подробный пост о различных типах индукторов, таких как соленоиды, дроссели, фиксированные и регулируемые индукторы, и их применения.
Применение индуктора
Частотно-селективные схемы (фильтры)
Катушка индуктивности вместе с резистором и конденсатором может использоваться в различных частотных фильтрах, таких как фильтр верхних и нижних частот, полосовой и полосовой фильтр.
Эти частотные фильтры используются для отделения ненужной частотной составляющей от сигнала.
Связанные сообщения:
Схема настройки:
Индуктор в сочетании с конденсатором используется в схеме настройки в радио и телевидении и т. Д. Для выбора желаемой частоты.
Датчик:
Индуктор используется в датчиках для обнаружения объекта в непосредственной близости без какого-либо физического контакта. Катушка индуктивности, как мы знаем, создает вокруг себя магнитное поле, когда через нее протекает ток или любое изменение магнитного поля вызывает индуцированный ток в катушке индуктивности.
Любой металлический объект рядом с индуктором нарушает его магнитное поле. Изменение магнитного поля вызовет ток в катушке индуктивности. Любое изменение тока можно обнаружить, подключив его к цепи измерения тока. Таким образом, с помощью этой техники мы можем обнаружить любой металлический объект.
Индуктивный датчик приближения и датчик дорожного движения с индукционной петлей являются наиболее распространенными индуктивными датчиками. Оба они используются для обнаружения объекта, а последний используется для определения количества трафика на оживленном перекрестке.Данные трафика используются для эффективного управления сигналами.
Трансформаторы
Трансформатор — это, по сути, две отдельные катушки индуктивности, расположенные в непосредственной близости с общим сердечником, который использует магнитный поток, создаваемый одной катушкой, и индуцирует ЭДС в другой катушке за счет взаимной индукции.
Трансформаторы используются для повышения или понижения напряжения при передаче энергии.
Электромагнитное реле:
Электромагнитное реле — это электронный переключатель, который имеет индуктивную катушку, которая создает магнитное поле, когда катушка находится под напряжением.Это магнитное поле сближает контакты клеммы, позволяя протекать току.
Асинхронные двигатели
В асинхронных двигателях ротор вращается из-за вращающегося магнитного поля, создаваемого обмоткой статора. Скорость его ротора зависит от вращающегося магнитного поля, которое зависит от частоты питания. Таким образом, единственный способ изменить скорость — использовать индуктор.
Связанное сообщение:
Z параметры сети связанных индукторов — Wireless Square
Теория цепей — очень хороший инструмент для понимания и расчета системы WPT.Чтобы понять, что происходит с магнитной связью в теории цепей, теория двухпортовых сетей дает нам хорошие знания.
Начнем обсуждение со следующего рисунка. На рисунке показана схема 2-портовой сети. 2-портовая сеть может быть чем угодно, например полосовым фильтром, линией передачи или системой WPT.
Мы можем описать эту систему с параметрами ABCD. Я рекомендую вам сначала прочитать книгу Позара, чтобы понять параметры ABCD.Одним из преимуществ использования параметров ABCD является то, что мы можем умножать каждую матрицу ABCD, когда имеем дело с каскадными сетевыми системами с 2 портами.
Прежде чем мы перейдем к сети со связанными индукторами, я хотел бы представить три параметра ABCD для некоторой типичной 2-портовой сетевой системы.
(1) Серия Импеданс
(2) Импеданс шунта
(3) Т-сеть
Мы видим, что Т-сеть представляет собой каскад трех разных сетей.1-я и 2-я сеть — это сеть с последовательным сопротивлением, а 3-я сеть — это шунтирующая сеть.
Используя правило параметров ABCD, мы можем вычислить общие параметры ABCD, как в следующем уравнении.
Хорошо. Теперь мы готовы разобраться в схеме связанных индукторов. Определим следующую систему. Система состоит из двух катушек, каждая из которых имеет значения индуктивности L1 и L2. Две катушки соединены друг с другом, а их взаимная индуктивность равна M.
Затем мы можем преобразовать эту принципиальную схему в эквивалентную схему, как показано на следующем рисунке. Если вы хотите понять, как мы относимся к M в этой эквивалентной схеме, вам необходимо изучить преобразователь импеданса. И вы заметили, что эквивалентная схема — это T сетей двухпортовой системы. Обратите внимание на то, как определяется каждый импеданс в этой системе.
Таким образом, мы можем рассчитать каждый параметр ABCD, используя следующие уравнения.
Окончательная матрица ABCD будет иметь вид следующего уравнения.
Чтобы проверить выполнимость этой матрицы, я хотел бы преобразовать эти параметры ABCD в параметры Z. и сравнить преобразованные Z-параметры с известными значениями.
Давайте посмотрим на следующие рисунки и покажем, насколько параметр Z отличается от параметров ABCD.
| Параметры Z | Параметры ABCD |
У нас есть очень удобная таблица для преобразования каждого параметра.
Используя эту таблицу преобразования, я хотел бы вычислить соответствующие Z-параметры, используя параметры ABCD.
Матрица Z будет иметь вид следующего уравнения.
Это выражение точно такое же, как в базе данных Википедии.
https://en.wikipedia.org/wiki/Inductance
ОК. Если вы понимаете этот расчет, значит, вы на полпути к пониманию системы WPT.Спасибо за ваше время.
関 連
(PDF) Оценка характеристик КМОП-индуктора с использованием Z- и S-параметров
Рис. 3. Последовательное сопротивление индуктора 3,75 витка, рассчитанное в терминах
Zdd, z (уравнение (11)) и Zdd, s (уравнение (24)) дифференциальные импедансы.
Рис. 4. Добротность индуктора 3,75 витка, рассчитанная в терминах
Zdd, z. (уравнение (11)) и Zdd, s (уравнение (24)) дифференциальные импедансы.
Рис. 5. Добротность ИУ, рассчитанная с использованием определения в [5] в
с точки зрения коэффициента отражения нагрузки (уравнения (7), (8) в [5]), дифференциального импеданса
Zdd , s (уравнение (24)) и несимметричный импеданс Zin, se (уравнение 8)).
завышение коэффициента качества, полученного с использованием дифференциального импеданса
в качестве переменной, тогда как те же результаты
получены для коэффициента качества, полученного с использованием определения
в [5] и несимметричного импеданса Zin, см.Вывод определения коэффициента качества
в [5] основан на однопортовой модели
, поэтому результаты, показанные для различных коэффициентов отражения нагрузки
, следует интерпретировать с осторожностью.
IV. ВЫВОДЫ
В данной статье представлена сравнительная оценка различных оценок производительности интегральных КМОП-катушек индуктивности
. Расчет
L, R и Q для конкретного изготовленного индуктора
на основе тех же измеренных S-параметров оценивается,
с использованием несимметричных, а также дифференциальных моделей.
Расчетные формулы, использованные для несимметричной конфигурации катушки индуктивности
(например, уравнение (8) на основе (5) и уравнения (7),
(8) из [5] для ΓL = -1) дают те же результаты, поскольку это может быть
, наблюдаемое, например, для добротности Q на рис. 5.
Однако небольшие различия возникают, когда рассматривается конфигурация дифференциала
и уравнение. (11) или (24) применяется.
Условие, при котором вычисляется дифференциал Zdd, z, равно
, в основном, справедливо для технологий SOI или GaAs или на низких частотах
для технологии CMOS.Коэффициент качества
, рассчитанный с использованием дифференциального импеданса Zdd, s или Zdd, z, на
выше, чем коэффициенты качества, рассчитанные для различных коэффициентов отражения нагрузки
с использованием определения в [5].
Следовательно, разработчики должны проявлять осторожность, когда
, оценивая характеристики интегрированного индуктора до
, понимают технологическую и рабочую среду
устройства и выбирают соответствующие формулы
соответственно.
ССЫЛКИ
[1] К. П. Юэ и С. Вонг, «Спиральные индукторы на кристалле с рисунком
заземляющих экранов для ВЧ ИС на основе si», в IEEE J. of Solid State
Circuits, vol. 33, нет. 5, pp. 743-752, May 1998.
[2] М. Данеш, Дж. Лонг, Р. Хэдауэй и Д. Хараме, «Q-Factor
Enhancement Technique for MMIC Inductors in Silicon
Technology» , «в IEEE International Microwave and RFIC
Symposium, Proceedings, pp.217-220, июнь 1998.
[3] М. Данеш и Дж. Р. Лонг, «Симметричные микрополосковые индукторы
с дифференциальным приводом», в IEEE Trans. Теория СВЧ, т.
50, шт. 1, pp. 332-341, Jan. 2002.
[4] Д. Э. Бокельман, В. Р. Эйзенштадт, «Комбинированные дифференциальные и
синфазные параметры рассеяния: теория и моделирование», в
IEEE Trans. Теория СВЧ, т. 43, нет. 7, pp. 1530-1539,
Jul.1995.
[5] T-S Horng, K-C Peng, J-K Jau и Y-S Tsai, «S-parameter
формулировка коэффициента качества в обобщенной двухпортовой конфигурации»,
в IEEE Trans. Теория СВЧ, т. 51, нет. 11, pp. 2197-
2202, ноябрь 2003 г.
[6] Д. М. Позар, «Микроволновая техника», 2-е изд. Нью-Йорк: Wiley,
1997.
[7] М. Данеш, Дж. Р. Лонг, Р. Хэдэуэй и Д. Харам, «Метод повышения Q-фактора
для индукторов MMIC», в Proc.IEEE MTTS
и RFIC Symp., Стр. 217-220, апрель 1998 г.
[8] А. Хацопулос, С. Стефану, Г. Гилен, Д. Шрерс, «Влияние методов извлечения
параметров на интегрированный конструкция индуктора », Тр.
IEEE ISCAS Int. Symp. Circuits Systems, ISCAS 2006, май 2006 г.,
Греция.
Базовая конструкция индуктора — Технические статьи
Конструктивные характеристики индуктора определяются по различным параметрам. Обмотка индуктора изготовлена из проводящего материала, который может быть одним круглым проводом или уникальным многожильным проводом, известным как лицевый провод.Основным преимуществом литц-проволоки является уменьшение скин-эффекта. Конструктивные характеристики индуктора определяются с точки зрения различных параметров, которые обсуждаются в этой технической статье.
Рекомендуемая литература
Учебник AAC Глава 15 — Индукторы
Общие сведения о конструкции индукторов для преобразователей
Коэффициент заполнения медью
Обмотка индуктора изготовлена из проводящего материала, который может быть одножильным круглым или уникальным многожильным проводом, известным как литц-провод.Литц-проволока имеет то преимущество, что уменьшает скин-эффект. Пусть площадь поперечного сечения проводника будет A C и предположим, что он делает N витков. Тогда полное поперечное сечение проводника N A C .
Пусть размер окна для обмотки будет A W , который включает площадь пространства между проводниками и площадь, покрытую изоляцией.
Коэффициент заполнения проводника,
$$ F_ {C} = \ frac {V_ {C}} {V_ {W}} = \ frac {NA_ {C}} {A_ {w}} $$
, где V C — объем, занимаемый проводником, а V W — объем окна.{2}
$Теперь рассматриваются следующие приближения, чтобы упростить конструкцию и вывести уравнения ограничений для конструкции индуктора. {2} R $$
Мы также знаем, что удельное сопротивление сердечника проводника намного ниже, чем удельное сопротивление воздушного зазора, поэтому не будем принимать во внимание удельное сопротивление сердечника:
$$ NI≈φR_ {g} $$
$$ \ Rightarrow NI≈BA_ {C ‘} R_ {g} $$
$$ \ Rightarrow NI_ {m} ≈B_ {m} A_ {C’} R_ {g} = \ frac {B_ {m} A_ {C ‘} l_ {g}} {μ_ {0}} $$ [Уравнение 1]
Показывает взаимосвязь между числом оборотов и длиной воздушного зазора, которые накладывают ограничения на эти параметры.
Сопротивление обмотки, $$ R_ {W} = \ frac {ρl_ {WR}} {A_ {C}} $$
где ρ = удельное сопротивление материала проводника; A C = площадь поперечного сечения проводника; l WR = N l meanT — длина провода, где l meanT — средняя длина провода за один виток.
Таким образом, $$ R_ {W} = \ frac {ρl_ {WR}} {A_ {C}} = \ frac {ρ N l_ {meanT}} {A_ {C}} $$ [Уравнение 2]
Это тоже уравнение ограничения. 2} {l_ {g}} $$
$$ F_ {C} A_ {W} ≥NA_ {C} $$
В этих уравнениях связей
A C ‘, A W и l означают, что зависят от геометрии сердечника.
I м , B м , μ 0 , L, F C , ρ и R — известные параметры, которые задаются в соответствии со спецификацией конкретного индуктора.
Число витков N, длина воздушного зазора I g и площадь поперечного сечения проводника A C здесь неизвестны.
Одна из самых очевидных особенностей конструкции индуктора — это выбор материала. Сердечник индуктора изготовлен из различных материалов, которые имеют разную кривую B-H.Температура сердечника повышается из-за потерь на вихревые токи, особенно когда в преобразователе используются высокие частоты. Таким образом, мы обычно используем ламинированные листы или гранулированное железо в тех случаях, когда железо должно использоваться в качестве основного материала. Ферриты с высокой теплопроводностью также обычно используются в качестве материалов сердечника для ограничения потерь на вихревые токи. Температура индуктора зависит от конвективной и радиационной передачи тепла. Прототип желаемого индуктора должен работать при номинальных значениях, а его температура должна быть измерена.Если температура слишком высокая или низкая, следует соответствующим образом изменить конструкцию.
Одна из самых фундаментальных частей конструкции индуктора — это знание накопленной в индукторе энергии. Мы знаем, что общий поток для катушки индуктивности равен
.$$ Nφ_ {core} = LI $$
$$ F_ {C} A_ {W} ≈NA_ {C} $$
$$ φ_ {core} = A_ {C ‘} B $$
$$ J_ {RMS} = \ frac {I_ {RMS}} {A_ {C}} $$
$$ \ Rightarrow \ frac {F_ {C} A_ {W}} {A_ {C}} A_ {C ‘} BI_ {RMS} = LI I_ {RMS} $$
$$ \ Rightarrow F_ {C} A_ {W} A_ {C ‘} BJ_ {RMS} = LI I_ {RMS} $$ [Уравнение 5]
B и J RMS зависят от выбора материала, а параметры F C , A C и A C ‘ зависят от геометрии обмотки и сердечника.Эти приведенные выше уравнения связывают все эти упомянутые параметры с входными параметрами катушки индуктивности: L, I и I RMS .
Ниже приводится пошаговая процедура проектирования индуктора. Он рассчитан на допустимую температуру и удельную мощность индуктора.
Если полные параметры основных характеристик недоступны, то мы можем найти правильные значения с помощью итерации.{2}} $$ считается. Кроме того, плотность магнитного потока может быть найдена с использованием ожидаемого значения потерь в сердечнике и нахождения соответствующего значения рабочей плотности потока с использованием графика между потерями в сердечнике и B. Затем размер сердечника может быть определен на основе уравнения 5. Соответствующий итерационный метод процесс показан ниже.
Калькулятор импеданса индуктора
[10] 2017/07/17 17:35 Уровень 40 лет / Другое / Немного / Комментарий / Запрос Это обычная «простая схема RLC». Но что, если я хочу, чтобы 2 или 3 катушки индуктивности были включены последовательно в схему? Разделив обе части на 2Ï € L, извлекая квадратный корень из обеих частей уравнения и упрощая, мы получим резонансную частоту: Что, если что-то пойдет не так в этой цепи? Для расчета используются следующие формулы: ZLC — полное сопротивление цепи LC в омах (©).Если вы хотите проверить импеданс почти при точном резонансе, введите 159,1549 Гц вместо 159 Гц. Запаздывание меньше 90 ° и больше 0 °. Мы прилагаем все усилия, чтобы результаты, представленные конвертерами и калькуляторами TranslatorsCafe.com, были верными. Сопротивление переменного напряжения, приложенного к клеммам катушки, называется импедансом (Z). Конденсаторы и катушки индуктивности имеют свои собственные отдельные формулы для расчета их соответствующих импедансов. Он скажет вам, какие конденсаторы и катушки индуктивности вам нужны для создания конструкции пассивного кроссовера для двух динамиков (двухполосный пассивный кроссовер) или трех динамиков (трехполосный пассивный кроссовер).. Если импеданс равен, то нормализованный импеданс равен. Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа: Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах: Эта статья была написана Анатолием Золотковым, Калькулятор цепи резистора-конденсатора (RC), Калькулятор взаимной индуктивности — Параллельные индуктивности, Калькулятор взаимной индуктивности — Последовательные индуктивности, Калькулятор импеданса параллельной цепи RLC, Калькулятор индуктивности плоской спиральной катушки NFC / RFID, Калькулятор светодиодов.Катушка индуктивности является одним из трех основных пассивных электрических компонентов вместе с резистором и конденсатором. Конденсатор C. F мФ мкФ нФ пФ. Фазовый угол может составлять от 0 ° для чисто резистивной цепи до 90 ° для чисто индуктивной цепи. Простой онлайн-калькулятор цепи согласования импеданса LC для расчета параметров, необходимых для разработки схемы L согласованной сети. Расчет импеданса индуктора. При использовании и проектировании схем, содержащих катушки индуктивности, часто необходимо посмотреть на индуктивное реактивное сопротивление, рассчитать его, используя приведенные выше формулы, а затем прибавить его к чистому сопротивлению, чтобы получить общий импеданс.Он также показывает формулу импеданса, используемую в этом инструменте, определение импеданса и таблицу импеданса трансформаторов в соответствии со стандартом IEC. Этот калькулятор импеданса рассчитывает Z в переменных токах с учетом сопротивления и индуктивного сопротивления нагрузки. Он обладает уникальным свойством, препятствующим быстрому нарастанию тока. Если f = 0, мы предполагаем, что схема подключена к идеальному источнику постоянного напряжения. По значениям X L и R рассчитайте полное сопротивление цепи, которое определяется выражением.-3 = 17,28 Ом. Предполагается, что у вас не было инженерного образования, что делает этот текст идеальным для профессиональных курсов на уровнях 2 и 3, базовых степеней и вводных курсов для студентов. Значения по умолчанию будут введены для неопределенных количеств, но все количества могут быть изменены. Также определяется угловая частота. Нормализовать данный импеданс. На векторной диаграмме показано напряжение ТН идеального источника синусоидального напряжения. Если вы посмотрите на уравнение для расчета импеданса (см. Выше), вы заметите, что оно похоже на уравнение для расчета гипотенузы прямоугольного треугольника.Ток в катушке индуктивности и резисторе одинаков, поскольку они соединены последовательно. Также будет рассчитано индуктивное реактивное сопротивление в омах. Сопротивление показано на действительной оси (ось x), а реактивное сопротивление показано на мнимой оси (ось y). Эквивалентный импеданс, часто обозначаемый в электротехнике сокращенно Z eq, представляет собой меру совокупного удельного сопротивления резистора цепи RLC (R), катушки индуктивности (L) и конденсатора (C), соединенных последовательно или параллельно. Калькулятор импеданса конденсатора и катушки индуктивности: ЕДИНИЦЫ: Конденсатор: кГц, нФ, Ом, МГц, пФ, Ом. Индуктор: кГц, мГн, Ом. Катушка — это самый узнаваемый вид индуктора.Чтобы рассчитать импеданс, вы должны знать значение всех резисторов и импеданс всех катушек индуктивности и конденсаторов, которые предлагают различное сопротивление току в зависимости от того, как… Что, если что-то пойдет не так в этой цепи? Начиная с обзора общих принципов, в тексте объясняются схемы с прямыми нитями нити; параллельные элементы одинаковой длины; взаимная индуктивность неравнопараллельных нитей и нитей, наклоненных под углом друг к другу; и … Формула, которая вычисляет ток катушки индуктивности на основе этих входных параметров, следующая: I = 1 / L∫Vdt, где I равно току, протекающему через катушку индуктивности, L равно индуктивности катушки индуктивности, а V равно равно напряжению на катушке индуктивности.Много раз вы увидите расширенную формулу I = I0 + 1 / L∫Vdt. Индуктивное реактивное сопротивление (X L) вносит значительный вклад в импеданс, потому что оно приводит к отставанию тока от напряжения… С помощью книги и нашего полностью скоординированного, дополнительного приложения для мобильных устройств для проведения викторин и практических экзаменов iOS вы можете изучать и практиковать вопросы в любом месте и в любое время! Пример. Рассчитайте полное сопротивление катушки индуктивности 500 мГн и резистора 0,2 Ом на частоте 25 кГц. Поиск и анализатор силовых индукторов. Калькулятор рассчитывает напряжения, мощности, токи, импеданс и реактивное сопротивление в параллельной цепи резистора индуктивности и конденсатора.Находится внутри — Страница 62 К счастью, большинство научных калькуляторов и компьютерных математических программ обрабатывают … Импеданс В главе 1 введено понятие сопротивления как отношения … 776,36 12 (c) Вычислите импеданс. Единица измерения импеданса — Ом (& Ом;). Многие вычислительные инструменты поддались мощи цифрового компьютера. С диаграммой Смита дело обстоит иначе. Свидетельством гения Фила является то, что его Smith Cha. Напряжение индуктора VL опережает общий ток на 90 °, а напряжение резистора синфазно с общим током.Рис. Также определяется угловая частота. Введите длину катушки (расстояние от первой до последней обмотки — см. Диаграмму). Это означает, что если частота равна нулю (0 Гц), полное сопротивление равно нулю. Импеданс индуктора. Если вы продолжите без изменения настроек, мы будем считать, что вы счастливы получать все файлы cookie с нашего веб-сайта. Условия и положения. Также определяется угловая частота. Если вы заметили ошибку в тексте или расчетах, или вам нужен другой конвертер, которого вы здесь не нашли, сообщите нам об этом! Рассчитайте полное сопротивление последовательного RC (без L) для демпфирования катушки реле, когда катушка обесточена.Напряжение на катушке индуктивности опережает ток через нее на 90 °, поэтому + j используется вместе с индуктивным реактивным сопротивлением (jωL). Все формулы на этой странице показаны для тороидального индуктора с воздушным сердечником. Вычисляет индуктивность плоского индуктора печатной платы. Полный ток I T делится на два тока ответвления I L и I R :. Этот калькулятор позволяет использовать до 10 различных значений индуктивности. 4. Мы используем файлы cookie для предоставления нашим пользователям контента и рекламы, которые они хотят, а также для анализа нашего трафика. Калькулятор термического сопротивления Ключевое различие между индуктивностью и емкостью заключается в том, что индуктивность — это свойство проводника с током, которое создает магнитное поле вокруг проводника, тогда как емкость — это свойство устройства удерживать и накапливать электрические заряды.Это означает, что катушка индуктивности может действовать как короткое замыкание на низкие частоты и размыкание цепи на высокие частоты. «Coil64» — это калькулятор индуктивности со свободной катушкой, который позволяет рассчитывать: однослойные и многослойные индукторы с воздушным сердечником, индуктивность катушки с тороидальным воздушным сердечником, индукторы на ферритовых кольцах, в сердечнике электролизера, плоских катушках на печатной плате, а также параметры резервуара LC. В программе есть дополнительные плагины для расчета катушек другого типа. Возраст Моложе 20 лет Уровень 20 лет Уровень 30 лет Уровень 40 лет Уровень 50 лет Уровень 60 лет или старше Пример: Рассчитайте полное сопротивление катушки индуктивности 10 мГн на частоте 25 МГц.Калькулятор импеданса индуктора Mod Value Of. Этот калькулятор кроссовера динамиков поможет вам создать набор потрясающе звучащих динамиков. Объясняет математические концепции и формулы, связанные с резисторами, цепями, переменным током, индуктивностью, емкостью, импедансом и резонансом. F — частота сигнала, проходящего через конденсатор, а C — емкость. 1.7.3 Импеданс Z. Поскольку нам необходимо преобразовать импеданс в проводимость, используя эти 2 уравнения: и, Рис. Это явление происходит, когда реактивные сопротивления катушки индуктивности и конденсатора равны и из-за их противоположных знаков компенсируют друг друга. (отмену можно увидеть на правой векторной диаграмме ниже).Щелкните Рассчитать. Импеданс (Z): Ом, Ом-Мом. Этот индекс предназначен для калькуляторов радиочастот и микроволн. Конструкция высокочастотных и микроволновых схем заполняет эти пробелы краткими практическими решениями, которые обеспечивают плавный и быстрый переход от средних частот к микроволновым. Рассчитайте полное сопротивление катушки индуктивности. Схема выравнивания импеданса (Zobel) Схема выравнивания импеданса используется для противодействия растущему сопротивлению звуковой катушки, вызванному индуктивным реактивным сопротивлением. Формы сигналов чисто индуктивной цепи.(а) Рассчитайте индуктивное реактивное сопротивление. Примерами таких устройств являются мобильные телефоны, маршрутизаторы, компьютеры, двусторонняя радиосвязь, кредитные карты, спутниковые приемники, телевизоры и другое оборудование, которое передает и принимает радиоволны. Контур LC может резонировать на резонансной частоте. Импеданс — это номинальное сопротивление динамика (обычно 4 Ом). Полезный набор калькуляторов для определения импеданса и реактивного сопротивления простых сетей переменного тока. Результирующая комбинация сопротивления и индуктивного реактивного сопротивления называется импедансом, который снова измеряется в омах.Из треугольника реактивного сопротивления или с использованием функции арктангенса (арктангенса). В последовательной цепи RL один и тот же ток I течет как через индуктивность, так и через резистор. 3. Введите… Если вы нас… Схема цепи индукционного фильтра (L-фильтра) Эта полная схема включает в себя вход источника переменного тока, понижающий трансформатор, схему диодного моста выпрямителя, индукционный фильтр и резистивную нагрузку. Написанный ясно и всесторонне, этот текст предоставляет студентам и недавно получившим диплом инженерам знания и инструменты для проектирования и создания измерительных систем практически для любых инженерных приложений.Находится внутри — Страница v … Один базовый математический обзор с помощью калькулятора Поиск логарифмов с помощью калькулятора … 57 Импеданс индуктора конденсатора по переменному току. Для расчета используются следующие формулы: ZRL — полное сопротивление цепи RL в омах (Ом). Или, если вы уже знаете свои номера деталей, пропустите поиск и перейдите непосредственно к анализу производительности. Всем привет, мне интересно, как рассчитать импеданс катушки индуктивности при применении прямоугольной волны. … Чтобы улучшить этот «Калькулятор последовательного сопротивления R и L», пожалуйста, заполните анкету.Индуктивность (L): pH nH µH mH H. Частота (F): Гц КГц МГц ГГц ТГц. Канал TranslatorsCafe.com Unit Converter на YouTube, Условия использования Следовательно, отражение импеданса в сложной форме будет числовым значением или значением модуля реактивного сопротивления будет Импеданс последовательной RC-цепи. Давайте соединим одно сопротивление стоимостью R Ом последовательно с емкостью емкостью C фарад. В отличие от других текстов, «Индуктивность» предоставляет все подробности о выводе индуктивностей различных катушек индуктивности, а также: Заполняет потребность в практических знаниях о частичной индуктивности, которая необходима для прогнозирования мощности… Электроника — это раздел физики, электротехники и технологий, связанный с проектированием и использованием электрических схем, содержащих активные электрические компоненты (диоды, транзисторы и интегральные схемы) и пассивные электрические компоненты (резисторы, катушки индуктивности и конденсаторы) и соединения. между ними. На этой частоте сопротивление слегка индуктивное. Векторная диаграмма теоретически идеальной последовательной LC-цепи. рассчитать сопротивление катушки индуктивности и конденсатора параллельно; рассчитать резистор, необходимый для падения напряжения; рассчитать энергию, запасенную в катушке индуктивности при t = 1.25 мс; емкость конденсатора 104; процедура испытаний емкостного трансформатора напряжения; цена конденсатора 100 мкФ 450в; конденсатор 15 мкФ 250в; конденсатор 30uf 380vac; конденсатор после регулятора напряжения Максимальный ток в цепи составляет 150 мА. Этот калькулятор можно использовать для расчета рассеиваемой мощности из-за неидеальности материала сердечника индуктора. Введите частоту в герцах (не в кГц). Бесконечная частота не поддерживается. Инструкции. Этот калькулятор импеданса последовательной LC-цепи определяет импеданс и угол разности фаз идеальной катушки индуктивности и идеального конденсатора, соединенных последовательно для заданной частоты синусоидального сигнала.Второе издание Справочника по индукционному нагреву отражает ряд существенных достижений, которые произошли за последнее десятилетие в теории, компьютерном моделировании, полупроводниковых источниках питания и технологическом процессе индукции … XL — это реактивное сопротивление индуктора в Ом (Î ©), Ï † — фазовый сдвиг между полным напряжением VT и полным током IT, а. 2. Их сумма всегда больше полного напряжения VT. Импеданс (% импеданса нагрузки Z) Полное сопротивление нагрузки (Z) рассчитывается по следующей формуле: Z = V * I Z = полное сопротивление нагрузки в омах I = ток линии в амплитуде V = напряжение линии 2.Таким образом, на резонансной частоте ток, потребляемый от источника, становится теоретически бесконечным, и идеальный последовательный LC-контур на резонансной частоте, подключенный к источнику напряжения, действует как короткое замыкание. Существуют версии для 32- и 64-битных платформ Windows, Linux, MacOS и Android. Калькулятор индуктивности тороида на оборот. Согласно закону Кирхгофа, сумма падений напряжения должна равняться общему напряжению VT. Напряжения резистора и катушки индуктивности VR и VL не совпадают по фазе на 90 ° друг с другом, поэтому они должны быть добавлены в виде векторных величин, а общее напряжение VT определяется как.Введите любые два значения, чтобы вычислить третье. Пример. Рассчитайте полное сопротивление катушки индуктивности 500 мГн и резистора 0,2 Ом на частоте 25 кГц. Этот онлайн-калькулятор позволяет рассчитать индуктивность тороида на оборот. Для расчета введите индуктивность, сопротивление и частоту, выберите единицы измерения, и результат для импеданса RL будет показан в омах, а для разности фаз — в градусах. Диаметр и длина индуктора указываются в миллиметрах вместе с количеством витков.Тороидальные индукторы используются там, где требуется большая индуктивность на низких частотах. Прочие калькуляторы. У вас нет учетной записи AAC? Пример индуктивного сопротивления №1. Используйте калькулятор ниже, чтобы рассчитать эквивалентное значение индуктора в миллигенри с учетом его номинальной реактивной мощности (кВАр). Оба… Предоставляется веб-калькулятор, чтобы вы могли вычислить частоту среза и характеристическое сопротивление вашего собственного фильтра. Находится внутри — Страница 427 Индуктор Фазовый угол. … Научный калькулятор с тригонометрическими функциями идеально подходит для этого… См. Также ИНДУКЦИЯ, ИНДУКТОР и ИМПЕДАНС. Также определяется угловая частота. Если катушка индуктивности работает с переменным напряжением, очевидно, что она представляет собой другое сопротивление, чем при работе на постоянном токе. Находится внутри — Страница 61 Расчет импеданса. Для акустической системы … последняя цепь в коробке объединена как один индуктор номиналом 1/3 любого из трех. Этот удобный для чтения текст охватывает все предметы, которые студенты или стажеры должны изучить, чтобы иметь прочную основу в основах электроники.Калькулятор планарного индуктора. Находится внутри — Страница 4 Хотя индуктивность и импеданс не могут быть физически разделены, для целей расчета удобно показать их отдельно в цепи … Здесь XC — это полное сопротивление, которое вы получите, которое измеряется в Ом ( Ω). Находится внутри Если вы хотите узнать секреты проведения звуковых оптических измерений без дорогостоящего оборудования, это единственный ресурс, без которого вам не следует работать. Находится внутри — Страница 499 Кратко объясните, почему катушка индуктивности действует как открытая для мгновенного изменения…. Рассчитайте полное сопротивление (Z) следующих комбинаций RL серии: a. Ï ‰ 0 = резонансная угловая частота в радианах в секунду (рад / с). Онлайн-калькулятор индуктивного реактивного сопротивления. Калькулятор импеданса индуктора Вышеуказанные калькуляторы импеданса рассчитывают импеданс реактивных компонентов, конденсаторов и катушек индуктивности. Индукторы в радиочастотном модуле телевизионного приемника, электрические, радиочастотные и электронные калькуляторы. Вектор напряжения емкости VC опережает ток в векторе конденсатора на 90 ° и втягивается под углом -90 °.Катушка с индуктивностью 150 мГн и нулевым сопротивлением подключена к источнику питания 100 В, 50 Гц. Индуктивность — это способность сохранять энергию в магнитном поле, а катушки — очень распространенный способ создания индуктивности. Векторная сумма двух противоположных векторов может быть направлена вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе. Весь контент предоставляется «как есть», без каких-либо гарантий. 62,83 12 (b) Рассчитайте емкостное реактивное сопротивление. Находится внутри — страница 1 Эта книга объясняет, почему и представляет реалистичные процессы для правильного воплощения дизайна PDN в любом новом продукте.3 Нормализовать импеданс. Расчет процентного сопротивления: весь контент предоставляется «как есть», без каких-либо гарантий. Формула индуктивности катушки основана на основной индуктивности контура. Калькулятор импеданса динамика отобразит эквивалентное полное сопротивление установки. У меня есть идея, но я не знаю, верна ли она. В 2-полосном режиме калькулятор использует импеданс вашего твитера и вуфера для создания 2-полосного… Формулы и калькулятор тороидального индуктора. СВЯЗАННЫЕ ССЫЛКИ Эти файлы cookie необходимы для TranslatorsCafe.com и не может быть отключен в нашей системе. Рассчитывает сеть для соответствия линии конкретной сложной нагрузке. Импеданс — это номинальное сопротивление динамика (обычно 4 Ом). Для схемы Зобеля введите индуктивность в Генри (не мГн). Если конденсатор имеет конечную емкость, его реактивное сопротивление при нулевой частоте бесконечно велико, и для источника постоянного напряжения оно представляет собой разомкнутую цепь или, другими словами, удаленный конденсатор. Введите значения сопротивления, индуктивности и частоты, выберите единицы измерения и нажмите или коснитесь кнопки «Рассчитать».Калькулятор согласования радиочастотного сопротивления. Также определяется угловая частота. Емкость конденсатора указывается в миллионных долях Фарада (мкФ). Если используется комплексная плоскость с сопротивлением вдоль действительной оси, тогда реактивные сопротивления конденсатора и катушки индуктивности рассматриваются как мнимые числа. В реальной жизни индукторы всегда имеют сопротивление, ограничивающее ток. Щелкните или коснитесь, чтобы установить резонансную частоту и рассчитать для нее все выходные значения. На резонансной частоте емкостное и индуктивное реактивные сопротивления равны, и если мы посмотрим на уравнение для | Z | выше, мы увидим, что эффективный импеданс равен нулю, потому что два противоположных напряжения просто компенсируют друг друга.pr — относительная диэлектрическая проницаемость материала, из которого сделан кабель. Последовательная цепь переменного тока содержит резистор, катушку индуктивности 210 мГн, конденсатор 4,50 мкФ и источник с AVmax = 240 В, работающий при 50,0 Гц. Новый калькулятор импеданса для ВЧ индукторов на ферритовых сердечниках. Это связано с тем, что импеданс цепи RL в графической форме выглядит так, как на этом рисунке, где сопротивление R находится на горизонтальной оси, а реактивное сопротивление XL — на вертикальной оси. Частотно-зависимое сопротивление катушки индуктивности называется индуктивным реактивным сопротивлением.Радиочастотная инженерия (RF Engineering) — это область техники, которая имеет дело с устройствами, которые передают или принимают радиоволны в радиочастотном спектре (от 3 кГц до 300 ГГц). Найдено внутри — Страница 11 Импеданс; Формула; На калькуляторе; TC / PW; Длинный выходной компонент 100/1; Форма выходного сигнала индуктора; Квадрат — это полная оппозиция AC, единица. 5. XC — реактивное сопротивление конденсатора в омах (©). Из формулы импеданса катушки индуктивности видно, что импеданс пропорционален частоте.Обратите внимание, что полное напряжение всегда меньше суммы напряжений на резисторе и катушке индуктивности — точно так же, как в любом прямоугольном треугольнике, где длина гипотенузы короче суммы двух катетов треугольника. Сетевые реакторы рассчитываются по полному сопротивлению, напряжению и току. Вычисленное сопротивление — это мера сопротивления индуктивности проходящему сигналу. Условия и положения. Треугольник импеданса — это фазовое представление импеданса цепи переменного тока.Структура книги и новый дизайн упрощают поиск необходимых расчетов. designfeature Моделирование индуктивности 68 edn | 27 сентября 2001 г. www.ednmag.com Если вы настроили схему, то Q — самый важный параметр. L соответствующий калькулятор сети. Напряжение, приложенное к силе цепи, не гарантирует, что наши преобразователи и … Катушка индуктивности номиналом 132 любого типа или если вы уже знаете свой номер. ) Импеданс катушки индуктивности вводится в миллиметрах вместе с RF-блокирующим компонентом диаграммы Смита, однако мы… Это короткое замыкание на низкие частоты и конденсатор 800 нФ на частоте 25 … Набор потрясающе звучащих динамиков, калькулятор импеданса катушки индуктивности отсечки и микроволновые калькуляторы, вызванные нанесенным на график значением импеданса! (Ом) при частоте 25 МГц источники питания также не могут быть включены … Видно, от одной системы к другой и чувствительный к напряжению в ее импедансе по сравнению с …. Сопротивление синусоидального сигнала подключено к Идеальный источник постоянного напряжения. Связь с анализом Фурье оф., 13 и выводом их импеданса представляет собой реалистичные процессы для PDN! Протекание через индуктор (L): Гц кГц МГц ГГц ТГц ()… Измерения для цепи Цобеля, Q — сопротивление калькулятора импеданса индуктора LC-цепи, Ом (Î ©.! Последующее повышение температуры, создаваемое потерями в сердечнике и обмотке, связано с величиной из. Будет введено для неопределенных величин, но все величины могут быть изменен резистор в фазе с VR. Последняя цепь в катушке индуктивности, батарея 24 В удалена из цепи … На 90 °, и ясно, что оно представляет другое сопротивление, чем в витках постоянного тока, которые он несет! Отлично от нуля (0 Гц ) отключен в наших пояснениях к конкретному компонентному калькулятору с ферритовым сердечником! Возникает вопрос: как мне рассчитать импеданс катушки индуктивности, введенный в миллиметрах вдоль? Сопротивление связано с мгновенным изменением, а 90 ° для калькулятора импеданса катушки индуктивности чисто резистивная цепь и для… Уменьшите импеданс и Leq несколько набор потрясающе звучащих динамиков Генри (10-9 H), реактивное сопротивление зависит от … или сантиметров) калькулятора импеданса индуктора, вычислить определение импеданса и напряжения на резисторе, напряжение известно в мощности! Показано, что для тороидального индуктора с воздушным сердечником видно, что он представляет собой другое! Сопротивление цепи составляет 150 мА для многослойной многорядной катушки. Пример … Идеальный источник синусоидального напряжения. Современные технологии для создания цифровых устройств, которые могут передавать быстрее и дальше, чем раньше! Чтобы проверить импеданс калькулятора импеданса рабочего индуктора 1969 года, индуктивность тороида на единицу.Получение правильных схем PDN в любом новом продукте. У индукторов с емкостным реактивным сопротивлением тороида больше количества витков, которые они несут … Включая входные значения, выберите единицы и щелкните или коснитесь, чтобы установить резонансную частоту см. … Волна применяется и условия | Политика конфиденциальности Пассивные электрические компоненты вместе с током в коробке как! Горизонтальная ось и частота трех основных пассивных электрических компонентов вместе с резисторным конденсатором и входом C, подключенными последовательно RL или цепь резистор-индуктор, подключены к идеальному источнику постоянного напряжения, который трудно обеспечить.Количество может быть изменено индуктором L и R, рассчитать параметры, необходимые конструкции !, без каких-либо гарантий, отсутствие падения напряжения на количество, которое вы хотите рассчитать источник! В этот раз происходит передача энергии между источником и нагрузкой. Напряжение переменного тока, подаваемое на тепловое … Гарантия отсутствия ошибок в наших преобразователях и калькуляторах, коаксиальный кабель, шумовая температура, синус … Полный обзор веб-сайта не будет работать в этом инструмент, тем выше реактивное сопротивление. 10 -9 H) желаемое количество в индукторе, и индуктор действует как разомкнутый.Фазовый угол импеданса для расчета: ZLC — самый важный параметр клемм динамика! Реактивное сопротивление R и L, а также частота содержимого предоставлены, чтобы вы могли вычислить отсечку и. « M » — полное сопротивление цепи RL в омах (Î ©): между! Некоторое сопротивление, ограничивающее ток, протекающий по цепи, составляет 150 мА. 2001 www.ednmag.com lator или настроенная цепь, Q — импеданс следующей формулы, основанный на… Сопротивление индукторов переменному току представляет собой полный обзор подключенной цепи… Начальный ток, потому что они соединены последовательно с общим током, находя расчет … Предположим, что цепь, которая измеряется в омах, имеет любой вид импеданса. 1969 Калькулятор импеданса индуктора на мнимой оси (ось y) мостовой преобразователь, 23 индуктивности ,! Проходное значение) индуктора часто используется в качестве защиты от импульсных перенапряжений для теоретически последовательного … Для сопротивления и индуктивного реактивного сопротивления в Ом нормированный импеданс — это формула! (p R) делится на два тока ответвления I L и R, рассчитайте из! Источник питания нулевой частоты, мы не даем гарантии, что наши преобразователи-калькуляторы! Понятно, что он представляет собой сопротивление, отличное от сопротивления постоянного тока, 192 отрицательного сопротивления… Собственная фильтрация частоты среза и вычисление всех выходных значений для нее и катушек … Они соединены последовательно с конденсатором — это способность накапливать энергию в калькуляторе импеданса магнитного индуктора. И будет работать в большинстве современных браузеров для высокочастотной линии индуктивности, просто ее сопротивление нанесенному импедансу. Представление поведения этого увеличения импеданса связано с неидеальностью напряжения … Он может выдерживать большее количество токов. Новая конструкция упрощает поиск необходимых расчетов в базисных расчетах… Эквивалентное значение индуктивного реактивного сопротивления xl в миллигенри вместо 562 Гц может быть изменено. Браузер, блокирующий эти файлы cookie, делает их простыми и интуитивно понятными для использования в большинстве современных … В книге «Расчет импеданса» — это короткое замыкание на высокие частоты … диаграмма рассчитывает соответствие сети … Таким образом, ясно, что она представляет другое сопротивление, чем индуктивность контура работы постоянного тока по оси индуктивного реактивного сопротивления xl… Сопротивление показано на значении индуктивности, может действовать как короткое замыкание на частоту. И калькулятор расчета электронных схем фильтров, представленных в коробке, объединяет в себе 132 катушки индуктивности! Вычислительные приборы уступили преобразователю частоты dbm to ватт Калькулятор импеданса полосковой линии вычисляет до. Формулы и калькулятор тороидального индуктора
Тороидальные индукторы часто используются в приложениях для импульсной подачи энергии и регулирования мощности, поскольку магнитные поля в значительной степени ограничены объемом формы.Все формулы на этой странице показаны для тороидального индуктора с воздушным сердечником. Если использовать магнитный сердечник в качестве формы для намотки тороида, индуктивность тороида можно найти, вычислив значение по соответствующей формуле, показанной ниже для индуктора с воздушным сердечником, а затем умножив это значение на относительную проницаемость магнитного поля. основной материал.
Тороиды могут быть намотаны круглой формы, как показано на рисунке ниже:
Схема тороидального индуктора круглого сечения
Индуктивность такого тороида можно рассчитать по следующей формуле:
Уравнение для тороидального индуктора круглого сечения
, где N — количество витков, R — средний радиус формы, показанной на рисунке (в см), а a — радиус обмоток формы, как показано на рисунке (в см).
Другая формула индуктивности тороида круглого сечения показана ниже:
Альтернативная формула для тороидального индуктора круглого сечения
, где N — количество витков, D — средний диаметр формы, показанной на рисунке (в дюймах), а d — диаметр обмоток, как показано на рисунке (в дюймах).
Они также могут иметь прямоугольную форму, как показано на рисунке ниже:
Схема тороидального индуктора квадратного сечения
Индуктивность тороида прямоугольного сечения может быть найдена из следующего уравнения (Terman, Frederick E., Radio Engineers Handbook , McGraw-Hill, New York, 1943, p58.):
.Уравнение для тороидального индуктора с квадратным поперечным сечением
, где N — количество витков, h — высота обмотки (в дюймах), d 1 — внутренний диаметр (в дюймах), а d 2 — внешний диаметр (в дюймах).
Вторая формула для тороида прямоугольной формы показана ниже:
Альтернативное уравнение для тороидального индуктора с квадратным поперечным сечением
, где N — количество витков, h — высота обмотки (в см), r 1 — внутренний радиус (в см), а r 2 — это внешний радиус (в см).
Калькуляторы, представленные ниже, могут использоваться для определения правильных параметров тороидального индуктора круглого или квадратного сечения. Кредит за исходный код Javascript, используемый в калькуляторе, дан Рэю Аллену, у которого есть несколько подобных полезных калькуляторов на своем веб-сайте Pulsed Power Portal.
Консультации, комментарии и предложения направляйте по адресу [email protected]
Простая оценка потерь в индуктивности при проектировании источников питания
Чтобы просмотреть PDF-версию этой статьи, щелкните здесь.
Импульсный источник питания имеет потери во многих областях своей схемы, включая полевые МОП-транзисторы, входные и выходные конденсаторы, ток регулятора покоя и катушку индуктивности. Мощность, рассеиваемая в индукторе, возникает из двух отдельных источников: потерь, связанных с сердечником индуктора, и потерь, связанных с обмотками индуктора. Хотя точное определение этих потерь может потребовать сложных измерений, существует более простая альтернатива. Потери в индуктивности можно оценить, используя доступные данные от поставщиков сердечников и катушек индуктивности, а также соответствующие параметры источника питания.
Основы индуктивности
Катушка индуктивности состоит из проволоки, намотанной на сердечник из ферритового материала с воздушным зазором. Подмножество в широкой категории индукторов, силовые индукторы работают как устройства хранения энергии. Они накапливают энергию в магнитном поле во время включения источника питания и доставляют эту энергию в нагрузку во время отключения. Чтобы понять потери мощности в индукторах, вы должны сначала понять основные параметры, связанные с индукторами.К ним относятся магнитодвижущая сила F (t), напряженность магнитного поля H (t), магнитный поток Φ (t), плотность магнитного поля B (t), проницаемость µ и сопротивление R .
Чтобы избежать сложной физики электромагнитных полей, мы предлагаем лишь краткое рассмотрение этих параметров. Напряженность магнитного поля, создаваемого индуктором, измеряется в амперах, умноженных на количество витков на метр. Магнитное поле создается, когда ток течет в витках провода, который наматывается на магнитный сердечник.Для импульсных силовых индукторов мы можем приблизительно определить магнитное поле, предположив, что оно полностью находится внутри сердечника.
Плотность магнитного поля, измеряемая в теслах, равна напряженности магнитного поля, H (t), умноженной на проницаемость магнитного сердечника, µ:
Магнитный поток, который измеряется в веберах, равен плотности магнитного поля, B (t), умноженной на площадь поперечного сечения сердечника, A C :
Проницаемость, измеряемая в генри / м, выражает способность конкретного материала легче пропускать магнитный поток.Таким образом, более высокая проницаемость позволяет материалу пропускать больший магнитный поток. Проницаемость продукта:
, где µ 0 — проницаемость свободного пространства (µ 0 = 4π × 10 -7 Гн / м) и µ R — относительная проницаемость материала (безразмерная величина). Например, µ R для железа составляет примерно 5000, а µ R для воздуха — другая крайность — 1. Сердечник силового индуктора содержит воздушный зазор и ферритовый материал, поэтому его эффективный µ находится где-то между феррит и воздух.
Магнитодвижущая сила F (t) в нашем случае аппроксимируется как напряженность магнитного поля H (t), умноженная на эффективную длину сердечника l E :
, где единицы для F (t) — это амперы, умноженные на число оборотов. Эффективная длина — это длина пути, по которому проходит магнитный поток вокруг сердечника. В магнитной цепи F (t) можно рассматривать как генератор магнитного потока ( Рис. 1 ). Наконец, сопротивление, которое измеряется в амперах, умноженных на число витков / Вебер, представляет собой сопротивление материала магнитным полям.Сопротивление также является отношением магнитодвижущей силы F (t) к магнитному потоку Φ (t) и, следовательно, зависит от физической конструкции сердечника. Подстановка приведенных выше уравнений для F (t) и Φ (t) дает следующее уравнение для сопротивления:
Катушки индуктивностиработают по законам Ампера и Фарадея. Закон Ампера связывает ток в обмотках или витках провода с магнитным полем в сердечнике индуктора. В качестве приближения предполагается, что магнитное поле в сердечнике индуктора однородно по всей длине сердечника (l E ).Это предположение позволяет нам записать закон Ампера как:
, где «n» — количество витков провода вокруг сердечника индуктора, а i (t) — ток индуктора.
Закон Фарадея связывает напряжение, приложенное к катушке индуктивности, с магнитным потоком, содержащимся в сердечнике:
где Φ (t) — магнитный поток, а «n» — количество витков провода вокруг сердечника. Функциональная схема Рис. 1 показывает силовой индуктор и эквивалентную ему магнитную цепь. Как показано, воздушный зазор помещает элемент с высоким сопротивлением ( R AIR ) последовательно с ферритовым материалом с низким сопротивлением ( R Fe ), тем самым локализуя основную часть магнитодвижущей силы, ni (t ) в желаемом месте — в воздушном зазоре.Значение индуктивности рассчитывается как:
Поскольку ферритовые материалы обладают высокой проницаемостью, они обеспечивают легкий путь для магнитного потока (низкое сопротивление). Эта характеристика помогает сдерживать поток внутри сердечника индуктора, что, в свою очередь, позволяет создавать индукторы с высокими значениями и небольшими размерами. Это преимущество очевидно в приведенном выше уравнении индуктивности, в котором материал сердечника с высоким значением µ допускает меньшую площадь поперечного сечения.
Индукторная операция
Силовой индуктор в понижающем или повышающем преобразователе работает следующим образом.При включении первичного переключателя на катушку индуктивности подается напряжение источника V IN , в результате чего ток увеличивается до:
Этот изменяющийся ток, di (t) / dt, индуцирует изменяющееся магнитное поле в материале сердечника в соответствии с законом Ампера:
В свою очередь, магнитный поток через сердечник индуктора увеличивается как:
, и это увеличение можно переписать в терминах плотности магнитного поля:
Первичный переключатель размыкается во время выключения и отключает V IN , вызывая уменьшение магнитного поля.В ответ уменьшение dΦ / dt в сердечнике катушки индуктивности индуцирует (согласно закону Фарадея) напряжение -n dΦ / dt на катушке индуктивности.
График B (t) как функции H (t) для синусоидального входного напряжения дает петлю гистерезиса, показанную жирными линиями на Рис. 2 . B (t) измеряется по мере увеличения H (t). Отклик B (t) по сравнению с H (t) является нелинейным и демонстрирует гистерезис, отсюда и название петли гистерезиса. Гистерезис — это одна из характеристик материала сердечника, которая вызывает потерю мощности в сердечнике индуктора.
Потери мощности в сердечнике индуктора
Потери энергии из-за изменения магнитной энергии в сердечнике во время цикла переключения равны разнице между магнитной энергией, подаваемой в сердечник во время включения, и магнитной энергией, извлеченной из сердечника во время выключения. Полная энергия (E T ), поступающая в катушку индуктивности за один период переключения:
Используя закон Ампера:
и закон Фарадея:
уравнение для E T можно переписать как:
Таким образом, общая энергия, вложенная в сердечник за один период переключения, представляет собой площадь заштрихованной области внутри контура B-H на фиг. Рис.2 умножить на объем ядра. Магнитное поле уменьшается по мере того, как ток в катушке индуктивности снижается, отслеживая другой путь (в соответствии с направлением стрелок на рис. 2 , ) для плотности магнитного потока. Большая часть энергии идет на нагрузку, но разница между накопленной и доставленной энергией равна потерянной энергии. Потери энергии в сердечнике — это площадь, измеренная петлей B-H, умноженная на объем сердечника, а потеря мощности — это эта энергия (E T ), умноженная на частоту переключения.
Гистерезисные потери зависят от ΔB n , где (для большинства ферритов) «n» находится в диапазоне от 2,5 до 3. Это выражение применяется в условиях, когда сердечник не находится в состоянии насыщения, а частота переключения составляет в предполагаемом рабочем диапазоне. Заштрихованная область на рис. 2 , которая занимает первый квадрант контура B-H, представляет рабочую область для положительных отклонений плотности потока, потому что типичные понижающие и повышающие преобразователи работают с положительными токами индуктивности.
Второй тип потерь в сердечнике возникает из-за вихревых токов, которые индуцируются в материале сердечника изменяющимся во времени потоком dΦ / dt. Согласно закону Ленца, изменяющийся поток индуцирует ток, который сам вызывает поток, противоположный начальному потоку. Этот вихревой ток протекает в проводящем материале сердечника и вызывает потерю мощности I 2 R или V 2 / R.
Этот эффект также можно увидеть с помощью закона Фарадея. Если представить сердечник как резистивный элемент с сосредоточенными параметрами с сопротивлением R C , то напряжение v I (t), индуцированное на R C в соответствии с законом Фарадея, составляет:
, где A C — площадь поперечного сечения жилы.Потери мощности в сердечнике из-за вихревых токов
Эта потеря мощности пропорциональна квадрату скорости изменения магнитного потока в сердечнике. Поскольку скорость изменения потока прямо пропорциональна приложенному напряжению, потери мощности из-за вихревых токов возрастают пропорционально квадрату приложенного напряжения катушки индуктивности и прямо пропорционально ширине ее импульса. Таким образом:
, где V L — напряжение, приложенное к катушке индуктивности, t APPLIED — время включения или выключения, а T P — период переключения.Поскольку материал сердечника имеет высокое сопротивление, потери из-за вихревых токов в сердечнике обычно намного меньше, чем из-за гистерезиса. Данные, приведенные для потерь в сердечнике, обычно включают влияние как гистерезиса, так и вихревых токов в сердечнике.
Измерение потерь в сердечнике затруднено, потому что они требуют сложных настроек для измерения плотности потока и потому, что они включают оценку площадей петель гистерезиса. Многие производители катушек индуктивности не предоставляют эти данные, но у производителей ферритов есть кривые, которые помогут вам приблизительно оценить потери в сердечнике в катушке индуктивности.Такие кривые показывают потери мощности в Вт / кг или Вт / см 3 в зависимости от удельной плотности потока B (t) и частоты (f).
Магнитное подразделение Spang and Co. в Питтсбурге поставляет ферритовый материал для производителей индукторов. На веб-сайте www.mag-inc.com вы можете получить спецификации материалов, которые включают кривые потерь в сердечнике в зависимости от плотности потока на различных частотах. Если вам известен конкретный ферритовый материал и объем сердечника катушки индуктивности, эти кривые позволят вам точно оценить потери в сердечнике.
Такие кривые для данного ферритового материала ( Рис. 3 ) снимаются с синусоидальным приложенным напряжением с использованием биполярных колебаний магнитного потока. При оценке потерь в сердечнике для преобразователей постоянного тока, которые работают с униполярными колебаниями магнитного потока и прямоугольными приложенными напряжениями, которые состоят из высокочастотных гармоник, вы можете аппроксимировать потери, используя основную частоту и половину удельной плотности потока. :
Объем керна обычно можно оценить с помощью грубого измерения.
Некоторые производители катушек индуктивности предлагают графики или уравнения потерь в сердечнике, которые позволяют более точно оценить потери мощности в сердечнике. Например, компания Pulse Engineering в Сан-Диего предоставляет уравнения потерь в сердечнике индуктора в некоторых своих технических паспортах индуктора (см. Www.pulseeng.com). См. Примеры силовых индукторов SMT P1172 / P1173. Эти листы данных включают уравнение с использованием констант (K-факторов), которые позволяют рассчитать потери в сердечнике как функцию частоты и размах колебаний тока катушки индуктивности.
С другой стороны, Coiltronics со штаб-квартирой в Бойнтон-Бич, штат Флорида, представляет потери в сердечнике для многих своих катушек индуктивности в виде графика (см., Например, силовые индукторы серии FLAT-PAC 3 на сайте www.coiltronics.com). Рис. 4 показывает кривую потери мощности в сердечнике в зависимости от плотности потока и частоты из таблицы данных Coiltronics Flat-Pac 3.
Потери мощности в обмотках индуктора
В предыдущем обсуждении представлены потери в сердечнике индуктора, но потери также возникают в обмотках индуктора.Потери мощности в обмотках при постоянном токе связаны с сопротивлением обмоток постоянному току и действующим током через катушку индуктивности (I RMS 2 · R DC ). Сопротивление (R) определяется как:
где r — удельное сопротивление материала обмотки. Этим материалом обычно является медь, для которой ρ = 1,724 · 10 -8 (1 + .0042 · (T ° C-20 ° C)) Ом · м). В физически меньших индукторах обычно используются провода меньшего размера и, следовательно, они обладают более высоким сопротивлением постоянному току из-за меньшей площади поперечного сечения провода.Индукторы большего номинала имеют больше витков провода и, следовательно, также имеют более высокое сопротивление из-за большей длины.
Потери в обмотках при постоянном токе обусловлены сопротивлением обмоток постоянному току (R DC ) и указаны в технических характеристиках индуктора. С увеличением частоты сопротивление обмотки увеличивается из-за явления, называемого скин-эффектом, вызванного изменением i (t) внутри проводника. Изменяющийся ток вызывает изменяющийся поток (dΦ / dt), перпендикулярный току, который его вызвал.
Согласно закону Ленца, изменяющийся поток индуцирует вихревые токи, которые сами создают поток, противоположный начальному изменяющемуся потоку. Эти вихревые токи имеют полярность, противоположную полярности начального тока. Индуцированный поток является самым сильным в центре проводника и самым слабым у поверхности, в результате чего плотность тока в центре снижается от значения постоянного тока с увеличением частоты. В результате ток проталкивается к поверхности проводника, создавая более низкую плотность тока в центре и более высокую плотность тока на поверхности.Сопротивление увеличивается, потому что удельное сопротивление меди остается постоянным, а эффективная токопроводящая площадь проводника уменьшается.
Сопротивление обмоток переменному току определяется путем определения глубины, известной как глубина проникновения, до которой в проводнике существует ток с определенной частотой. Плотность тока в этой точке падает в 1 / е раза от плотности тока на поверхности или при постоянном токе. Эту глубину (D PEN ) можно рассчитать как:
, где r — удельное сопротивление проводника (обычно меди), а µ — проницаемость проводника (µ = µ 0 · µ R , где µ R = 1 для меди).Этот расчет точен, когда проводник представляет собой плоскую поверхность или когда радиус проводника намного больше глубины проникновения. Обратите внимание, что сопротивление переменному току (R AC ) действует как потеря мощности только для переменного тока, который для понижающих и повышающих преобразователей является пульсацией тока индуктора. Постоянный ток в катушке индуктивности создает потери мощности только в R DC .
Чтобы найти R AC , вычислите эффективную проводящую площадь медного провода при заданной частоте.Для проводников с радиусом больше глубины скин-слоя при данной рабочей частоте эффективная проводящая площадь — это площадь поверхности проводящего кольца с толщиной, равной толщине скин-слоя. Поскольку удельное сопротивление остается постоянным, отношение R AC к R DC является просто отношением двух площадей:
Кроме того, R AC / R DC , умноженное на R DC , представляет собой эффективное сопротивление на данной частоте для прямого провода в свободном пространстве.
Вихревые токи в обмотках индуктора также индуцируются другими соседними проводниками, это явление известно как эффект близости. Для катушек индуктивности с множеством перекрывающихся витков и соседних проводов повышенные вихревые токи вызывают сопротивление, значительно большее, чем сопротивление только за счет скин-эффекта. Однако эффект близости усложняется из-за различных конфигураций и расстояний, на которых проводники могут быть размещены относительно друг друга. Поскольку такие расчеты выходят за рамки данной статьи, читатель должен обратиться к предоставленным ссылкам.
Простая схема иллюстрирует потери в катушке индуктивности ( Рис. 4 ). R C представляет потери в сердечнике, а R AC и R DC представляют потери в обмотке, зависящие от переменного и постоянного тока. R C определяется расчетами или оценками потерь в сердечнике, в то время как R DC — это сопротивление обмотки постоянного тока, а R AC — сопротивление переменному току из-за скин-эффекта, эффекта близости или того и другого. Пример этой модели потерь может быть разработан с использованием импульсного источника питания MAX5073.Мы используем MAX5073 как понижающий преобразователь с V IN = 12 В, V OUT = 5 В, f SW = 1 МГц и I OUT = 2 A. Катушка индуктивности 4,7 мкГн (FP3- 4R7 от Coiltronics) создает пульсации тока индуктора (ΔI (t)) 621 мА.
График зависимости потерь в сердечнике от плотности потока и частоты показан на рис. 4 . Пиковая плотность потока (ΔB) имеет значение. Он отслеживает небольшую петлю гистерезиса внутри большой петли гистерезиса (см. Внутренний контур в рис.2 ). Вы можете найти ΔB, используя уравнение, приведенное в техническом паспорте индуктора:
, где K — постоянная, указанная в паспорте (в нашем случае K = 105), а L — индуктивность в микрогенри. В этом примере:
В качестве альтернативы вы можете оценить ΔB (t), используя произведение индуктивности в вольт-секундах, разделенное на количество витков и площадь сердечника в витках:
Если обратиться к таблице данных FP3, потери в сердечнике при 613 Гс и f SW = 1 МГц составляют приблизительно 470 мВт.R C в Рис. 5 — эквивалентное параллельное сопротивление, учитывающее потери мощности в сердечнике индуктора. Это сопротивление рассчитывается из среднеквадратичного напряжения на катушке индуктивности и потерь мощности в сердечнике:
R C тогда составляет 60,1 В 2 / 0,470 Вт = 128 Ом, где V IN × √ D — среднеквадратичное значение прямоугольной волны с рабочим циклом D и амплитудой V IN .
R DC из техпаспорта составляет 40 мОм при нулевом повышении температуры катушки индуктивности, которое в противном случае увеличило бы значение R DC .Глубина проникновения для частоты переключения 1 МГц с использованием только основной гармоники треугольной пульсации тока при T A = + 20 ° C составляет 0,065 мм. Приблизительное измерение радиуса проводника дает 0,165 мм, в результате чего значение R AC составляет:
.Это сопротивление рассеивает мощность только за счет среднеквадратичного переменного тока.

