Сила тока при последовательном. Последовательное и параллельное соединение проводников: основные характеристики и применение

Как работает последовательное соединение проводников. Чем отличается параллельное соединение. Какие законы описывают эти типы соединений. Где применяются последовательные и параллельные цепи.

Последовательное соединение проводников: основные характеристики

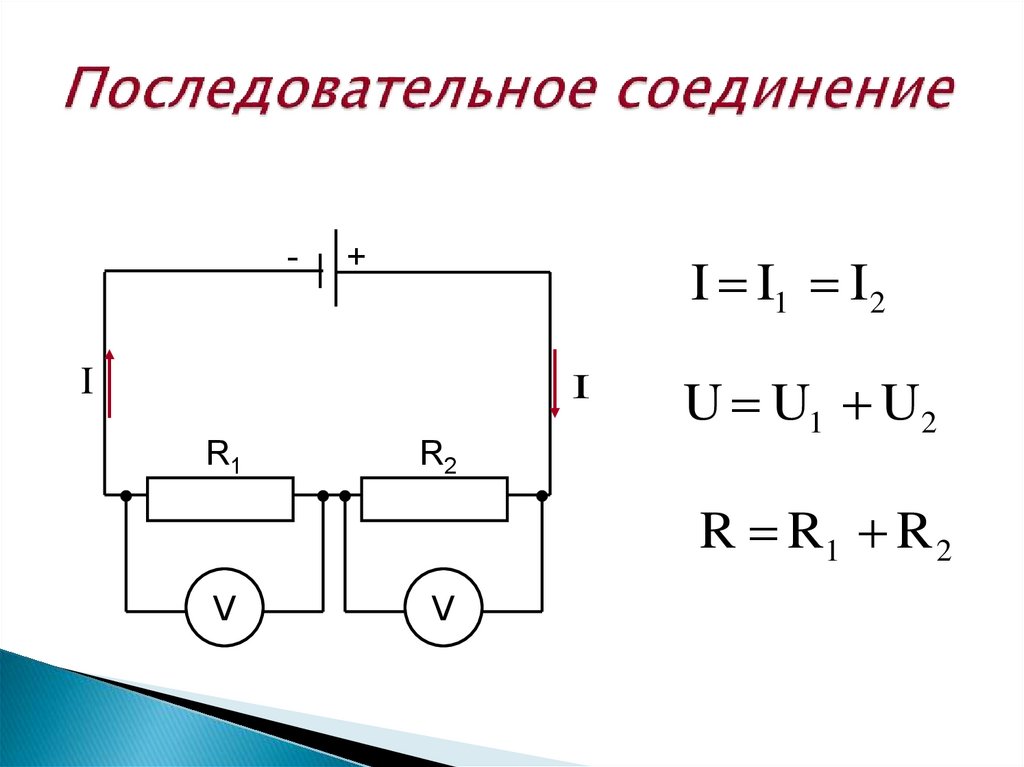
При последовательном соединении проводники включаются в цепь друг за другом, без разветвлений. Основные свойства такой цепи:

• Сила тока одинакова во всех участках цепи: I = I1 = I2 = … = In
• Общее напряжение равно сумме напряжений на отдельных участках: U = U1 + U2 + … + Un
• Общее сопротивление равно сумме сопротивлений отдельных проводников: R = R1 + R2 + … + Rn

Как работает последовательное соединение. Ток, проходя через первый проводник, затем проходит через второй и так далее. При этом на каждом участке происходит падение напряжения.

Параллельное соединение проводников и его особенности

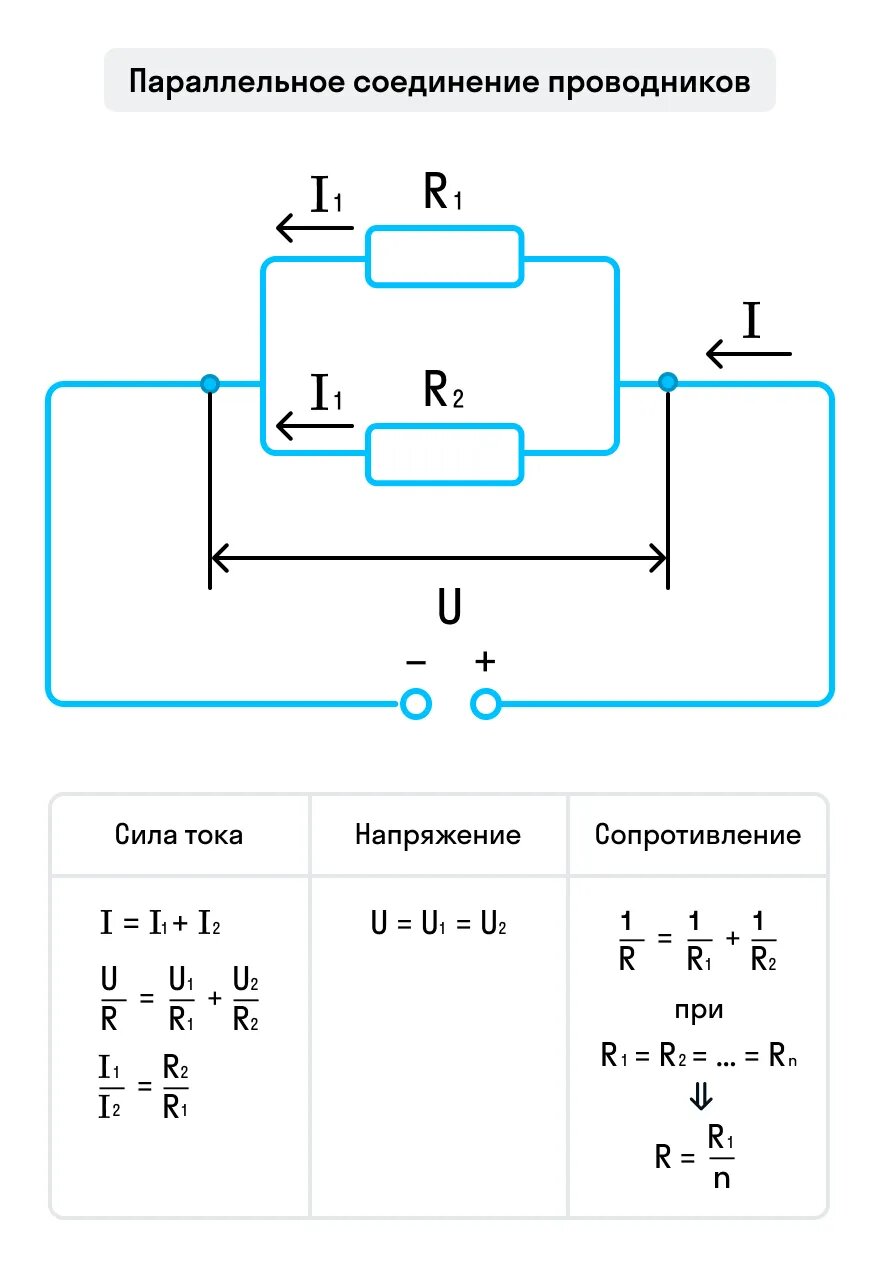
При параллельном соединении все проводники подключаются к общим точкам цепи. Характерные черты такой схемы:

• Напряжение на всех участках одинаково: U = U1 = U2 = … = Un
• Общий ток равен сумме токов в отдельных ветвях: I = I1 + I2 + … + In
• Обратная величина общего сопротивления равна сумме обратных величин сопротивлений отдельных проводников: 1/R = 1/R1 + 1/R2 + … + 1/Rn

Чем отличается параллельное соединение от последовательного. При параллельном подключении ток разветвляется по проводникам, а затем снова соединяется. Напряжение на всех участках одинаково.

Законы Кирхгофа для электрических цепей

Поведение тока и напряжения в разветвленных цепях описывается законами Кирхгофа:

1. Первый закон Кирхгофа: сумма токов, втекающих в узел, равна сумме токов, вытекающих из него.
2. Второй закон Кирхгофа: алгебраическая сумма напряжений вдоль любого замкнутого контура равна нулю.

Какие законы описывают последовательные и параллельные цепи. Для последовательного соединения применяется второй закон Кирхгофа, для параллельного — первый закон Кирхгофа.

Расчет сопротивления при различных соединениях

При последовательном соединении общее сопротивление увеличивается:

R = R1 + R2 + … + Rn

При параллельном соединении общее сопротивление уменьшается:

1/R = 1/R1 + 1/R2 + … + 1/Rn

Для двух параллельно соединенных проводников:

R = (R1 * R2) / (R1 + R2)

Применение последовательного и параллельного соединения

Где применяются последовательные цепи:

• Елочные гирлянды
• Предохранители и выключатели
• Делители напряжения
• Измерительные приборы с добавочными сопротивлениями

Где используется параллельное соединение:

• Бытовая электропроводка
• Многоламповые осветительные приборы
• Параллельное включение аккумуляторов
• Шунты для измерительных приборов

Смешанное соединение проводников

На практике часто встречаются цепи со смешанным соединением, сочетающим последовательные и параллельные участки. Расчет таких цепей проводится поэтапно:

1. Цепь разбивается на простые последовательные и параллельные соединения
2. Рассчитываются эквивалентные сопротивления для каждого участка
3. Постепенно цепь упрощается до одного эквивалентного сопротивления

Преимущества и недостатки различных типов соединений

Последовательное соединение:

Преимущества:

• Простота подключения
• Возможность использования элементов с разными номинальными токами

Недостатки:

• При выходе из строя одного элемента прерывается вся цепь
• Общее напряжение должно быть достаточным для всех элементов

Параллельное соединение:

Преимущества:

• Независимая работа потребителей
• Возможность подключения элементов с разными сопротивлениями

Недостатки:

• Необходимость большего тока от источника питания
• Сложность обеспечения равномерной нагрузки по ветвям

Методы измерения в электрических цепях

Для измерения характеристик электрических цепей используются различные приборы:

• Амперметр — для измерения силы тока (включается последовательно)
• Вольтметр — для измерения напряжения (включается параллельно)
• Омметр — для измерения сопротивления
• Мультиметр — комбинированный прибор для различных измерений

При измерениях следует учитывать влияние самих приборов на цепь. Например, для точного измерения напряжения вольтметр должен иметь большое внутреннее сопротивление.

Практические задачи на расчет цепей

Рассмотрим несколько типовых задач:

1. Три резистора с сопротивлениями 10 Ом, 20 Ом и 30 Ом соединены последовательно. Найти общее сопротивление цепи.

Решение: R = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ом

2. Два резистора 100 Ом и 200 Ом соединены параллельно. Рассчитать эквивалентное сопротивление.

Решение: 1/R = 1/R1 + 1/R2 = 1/100 + 1/200 = 3/200

R = 200/3 ≈ 66.7 Ом

3. В цепи с напряжением 12 В последовательно соединены две лампы с сопротивлениями 20 Ом и 40 Ом. Найти силу тока в цепи и напряжение на каждой лампе.

Решение:

Общее сопротивление: R = R1 + R2 = 20 + 40 = 60 Ом

Сила тока: I = U/R = 12/60 = 0.2 А

Напряжение на первой лампе: U1 = I * R1 = 0.2 * 20 = 4 В

Напряжение на второй лампе: U2 = I * R2 = 0.2 * 40 = 8 В

Заключение

Понимание принципов последовательного и параллельного соединения проводников является фундаментальным для работы с электрическими цепями. Эти знания позволяют:

• Правильно проектировать электрические схемы
• Рассчитывать параметры цепей
• Эффективно использовать электроприборы
• Обеспечивать безопасность электрических систем

Применение этих принципов охватывает широкий спектр областей — от бытовой электроники до промышленных электросистем. Дальнейшее изучение электротехники позволит глубже понять сложные электрические явления и их практическое применение.

Последовательное соединение проводников | Физика

Электрические цепи, используемые на практике, содержат, как правило, несколько потребителей электроэнергии. Эти потребители могут быть по-разному соединены друг с другом, например последовательно или параллельно.

При последовательном соединении потребителей они включаются в цепь поочередно друг за другом без разветвлений проводов между ними. Именно так соединены резисторы, изображенные на рисунке 41. Форма линий, обозначающих при этом соединительные провода, не играет роли, и потому схема цепи при одном и том же типе соединения может выглядеть по-разному.

Обозначим через I₁, U₁ и R₁ силу тока, напряжение и сопротивление на первом участке цепи (первом резисторе на рисунке 41, а), а через I₂, U₂ и R₂ силу тока, напряжение и сопротивление на втором участке цепи (втором резисторе на рисунке 41, а). Общее сопротивление обоих участков обозначим через R, общее напряжение на них — через U, а общую силу тока, которая совпадает с силой тока внутри источника, — через I. Тогда связь между общими значениями силы тока, напряжения и сопротивления с их значениями на отдельных участках цепи может быть выражена в виде следующих соотношений:

I = I₁ = I₂, (16.1) U = U₁ + U₂, (16.2) R = R₁

+ R₂. (16.3)

Чтобы убедиться в справедливости этих соотношений, следует собрать соответствующую цепь и с помощью амперметра и вольтметра произвести необходимые измерения.

Итак, при последовательном соединении проводников сила тока везде одинакова, напряжение в цепи равно сумме напряжений на отдельных участках, а общее сопротивление складывается из сопротивлений отдельных проводников.

Соотношения (16.1)-(16.3) допускают обобщение: все приведенные закономерности справедливы для любого числа последовательно соединенных проводников.

Из равенства (16.3) следует, что общее сопротивление последовательно соединенных проводников всегда превышает сопротивление любого из них. Это и понятно: ведь, соединяя проводники последовательно, мы как бы увеличиваем их общую длину, а с увеличением длины возрастает и сопротивление.

При последовательном соединении n одинаковых элементов (резисторов, ламп и т. д.) их общее сопротивление R превышает сопротивление R

1 одного из них в n раз:

R = nR₁

Общее напряжение U при этом делится на n равных частей, так что каждый из элементов цепи оказывается под напряжением U1 в n раз меньшим общего значения. Например, при включении в сеть с напряжением U = 220 В десяти последовательно соединенных одинаковых ламп каждая из них оказывается под напряжением U₁ = U/10 = 22 В.

Отличительной особенностью последовательного соединения проводников является то, что при отказе в работе хотя бы одного из них ток прекращается сразу во всей цепи. Вывернув, например, одну из ламп, изображенных на рисунке 42, мы увидим, как тут же перестанет гореть и другая (оставшаяся) лампа. Так что, если вы украсите новогоднюю елку гирляндой из последовательно соединенных лампочек и какая-то из них перегорит, то погаснет не только она, но и все остальные тоже.

Поэтому, чтобы определить, какая из лампочек перегорела, вам придется проверить всю гирлянду.

1. Какое соединение проводников называют последовательным? 2. Начертите схему цепи, изображенной на рисунке 42. 3. Какие три закономерности справедливы для последовательного соединения проводников? 4. Как находится общее сопротивление последовательно соединенных проводников в случае, когда они одинаковые? Как в этом случае распределяется между проводниками общее напряжение?

Как изменяется сила тока при параллельном соединении. Последовательное и параллельное соединение проводников

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.

На рисунке 78, а изображена цепь последовательного соединения двух электрических ламп, а на рисунке 78, б — схема такого соединения.

Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.

Рис. 78. Последовательное включение лампочек и источников питания

Последовательно соединены, например, аккумулятор, лампа, два амперметра и ключ в цепи, изображённой на рисунке 62 (см. § 38).

Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же , т. е.

А чему равно сопротивление последовательно соединённых проводников?

Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):

Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:

U 1 = IR 1 , U 2 = IR 2 .

Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи :

Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.

Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.

Пример 1 . Два проводника сопротивлением R 1 = 2 Ом, R 2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Запишем условие задачи и решим её.

Вопросы

1. Какое соединение проводников называют последовательным? Изобразите его на схеме.
2. Какая электрическая величина одинакова для всех проводников, соединённых последовательно?
3. Как найти общее сопротивление цепи, зная сопротивление отдельных проводников, при последовательном соединении?
4. Как найти напряжение участка цепи, состоящего из последовательно соединённых проводников, зная напряжение на каждом?

Упражнение

1. Цепь состоит из двух последовательно соединённых проводников, сопротивление которых 4 и 6 Ом. Сила тока в цепи 0,2 А. Найдите напряжение на каждом из проводников и общее напряжение.
2. Для электропоездов применяют напряжение 3000 В. Как можно использовать для освещения вагонов лампы, рассчитанные на напряжение 50 В каждая?
3. Две одинаковые лампы, рассчитанные на 220 В каждая, соединены последовательно и включены в сеть с напряжением 220 В. Под каким напряжением будет находиться каждая лампа?
4. Электрическая цепь состоит из источника тока — батареи аккумуляторов, создающей в цепи напряжение 6 В, лампочки от карманного фонаря сопротивлением 13,5 Ом, двух спиралей сопротивлением 3 и 2 Ом, ключа и соединительных проводов. Все детали цепи соединены последовательно. Начертите схему цепи. Определите силу тока в цепи, напряжение на концах каждого из потребителей тока.

1 Какое надо взять сопротивление R, чтобы можно было включить в сеть с напряжением V=220 В лампу, рассчитанную на напряжение Vо = 120 В и ток Iо = 4 А?

2 Две дуговые лампы и сопротивление R соединены последовательно и включены в сеть с напряжением V=110В. Найти сопротивление R, если каждая лампа рассчитана на напряжение Vо = 40 В, а ток в цепи I=12 А.

Напряжение на сопротивлении

По закону Ома

3 Для измерения напряжения на участке цепи последовательно включены два вольтметра (рис. 88). Первый вольтметр дал показание V1 = 20 В, второй- V2 = 80 В. Найти сопротивление второго вольтметра R2, если сопротивление первого вольтметра R1 = 5 кОм.

Через вольтметры протекает один и тот же ток I. Так как вольтметр показывает напряжение на собственном сопротивлении, то

и сопротивление второго вольтметра

4 Реостат из железной проволоки, миллиамперметр и источник тока включены последовательно. При температуре to = 0° С сопротивление реостата Ro = 200 Ом. Сопротивление миллиамперметра R = 20 Ом, его показание Iо = 30 мА. Какой ток It будет показывать миллиамперметр, если реостат нагреется до температуры t = 50° С? Температурный коэффициент сопротивления железа .

Последовательное и параллельное соединения проводников. Добавочные сопротивления и шунты

5 Проводник с сопротивлением R = 2000 Ом состоит из двух последовательно соединенных частей: угольного стержня и проволоки, имеющих температурные коэффициенты сопротивления . Какими следует выбрать сопротивления этих частей, чтобы общее сопротивление проводника R не зависело от температуры?

При температуре t общее сопротивление последовательно включенных частей проводника с сопротивлениями R1 и R2 будет

где R10 и R20 — сопротивления угольного стержня и проволоки при t0=0° С. Общее сопротивление проводника не зависит от температуры, если

В этом случае при любой температуре

Из последних двух уравнений найдем

6 Составить такую схему электропроводки для освещения одной лампочкой коридора, которая позволяет включать и выключать свет независимо в любом конце коридора.

Схемы электропроводки, позволяющие включать и выключать лампочку в любом конце коридора, показаны на рис. 347. У концов коридора устанавливаются два переключателя П1 и П2 каждый из которых имеет два положения. В зависимости от расположения выводов от сети может оказаться выгоднее с точки зрения экономии проводов вариант а) или б).

7 В сеть с напряжением V= 120 В включены две электрические лампочки с одинаковыми сопротивлениями R = 200 Ом. Какой ток пойдет через каждую лампочку при их параллельном и последовательном соединениях?

I1 = V/R=0,6 А при параллельном соединении; I2=V/2R=0,3 А при последовательном соединении.

8 Реостат со скользящим контактом, соединенный по схеме, приведенной на рис. 89, является потенциометром (делителем напряжения). При перемещении движка потенциометра снимаемое с него напряжение Vx изменяется от нуля до напряжения на клеммах источника тока V. Найти зависимость напряжения Vx от положения движка. Построить график этой зависимости для случая, когда полное сопротивление потенциометра Ro во много раз меньше сопротивления вольтметра r.

Пусть при данном положении движка сопротивление участка ах потенциометра равно rх (рис. 89). Тогда общее сопротивление этого участка и вольтметра (они соединены параллельно) а сопротивление остальной части потенциометра xb равно Таким образом, полное сопротивление между точками а и b будет

Ток в цепи I= V/R. Напряжение на участке ах

Так как по условию R0

т.е. напряжение Vх пропорционально сопротивлению rх. В свою очередь сопротивление rх пропорционально длине участка ах.

На рис. 348 сплошная прямая показывает зависимость Vx от rх, штрихпунктирная линия — зависимость Vx от rх, когда R0~r, т. е. когда в выражении для Vх нельзя пренебречь первым членом в знаменателе. Эта зависимость не является линейной, однако и в этом случае Vx изменяется в пределах от нуля до напряжения на клеммах источника V.

9 Найти сопротивление R биметаллического (железо- медь) провода длины l=100м. Диаметр внутренней (железной) части провода d=2 мм, общий диаметр провода D = 5 мм. Удельные сопротивления железа и меди . Для сравнения найти сопротивления железного и медного проводов Яж и Rм диаметра D и длины l.

Площади сечения железной и медной частей провода

(рис. 349). Их сопротивления

Сопротивление R биметаллического провода находится по формуле параллельного соединения проводников:

Сопротивления железного и медного проводов диаметра D и длины l

10 Найти общее сопротивление проводников, включенных в цепь по схеме, изображенной на рис. 90, если сопротивления R1= = R2 = R5 = Я6 = 1 Ом, R3 = 10 Ом, R4 = 8 Ом.

11 Общее сопротивление двух последовательно соединенных проводников R=5 Ом, а параллельно соединенных Rо=1,2 Ом. Найти сопротивление каждого проводника.

При последовательном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление

а при параллельном соединении

Согласно известному свойству приведенного квадратного уравнения (теорема Виета) сумма корней этого уравнения равна второму его коэффициенту с обратным знаком, а произведение корней-свободному члену, т. е. R1 и R2 должны быть корнями квадратного уравнения

Подставив значения Rо и R, найдем R1 = З Ом и R2 = 2 0м (или R1 =2 Ом и R2 = 3 Ом).

12 К проволочному кольцу в двух точках присоединены подводящие ток провода. В каком отношении делят точки присоединения длину окружности кольца, если общее сопротивление получившейся цепи в n = 4,5 раза меньше сопротивления проволоки, из которой сделано кольцо?

Точки присоединения подводящих проводов делят длину окружности кольца в отношении 1:2, т. е. отстоят друг от друга по дуге на 120град.

13 В цепи, изображенной на рис. 91, амперметр показывает ток I=0,04 А, а вольтметр — напряжение V=20 В. Найти сопротивление вольтметра R2, если сопротивление проводника R1 = 1 кОм.

14 Найти сопротивление R1 лампочки по показаниям вольтметра (V=50 В) и амперметра (I=0,5 А), включенных по схеме, изображенной на рис. 92, если сопротивление вольтметра R2 = 40 кОм.

Ток в общей цепи I=I1+I2, где I1 и I2 — токи, текущие через лампочку и вольтметр. Так как

Пренебрегая током I2 = 1,25мА по сравнению с I=0,5 А получим по приближенной формуле

то же значение сопротивления лампочки: R1 = 100 Ом.

15 Найти сопротивление проводника R1 по показаниям амперметра (I=5 А) и вольтметра (V=100В), включенных по схеме, изображенной на рис. 93, если сопротивление вольтметра R2 = 2,5 кОм. Какова будет ошибка в определении R1, если, предположив, что , при расчетах пренебречь током, текущим через вольтметр?

Показание вольтметра

где I1 и I2-токи, текущие через сопротивление и вольтметр. Общий ток

Если пренебречь током I2 по сравнению с I, то искомое сопротивление

Ошибка в определении R`1 будет

Учитывая, что

найдем относительную ошибку:

16 К источнику тока с напряжением V присоединены последовательно два проводника с одинаковыми сопротивлениями R. Какова будет разница в показаниях вольтметров с сопротивлениями R и 10R, если их поочередно подключать к концам одного из проводников?

Вольтметры с сопротивлениями R и 10R показывают напряжения

поэтому разница в показаниях вольтметров

17 К источнику тока с напряжением V= 12 В присоединены две лампочки (рис. 94). Сопротивления участков цепи r1 = r2 = r3 = r4 = г = 1,5 Ом. Сопротивления лампочек R1 = R2 = R = 36 Ом. Найти напряжение на каждой лампочке.

18 В схеме, изображенной на рис. 95, напряжение источника тока V=200 В, а сопротивления проводников R1=60Ом, R2 = R3 = 30 Ом. Найти напряжение на сопротивлении R1.

19 Электрическая цепь состоит из источника тока с напряжением V=180В и потенциометра с полным сопротивлением R = 5 кОм. Найти показания вольтметров, присоединенных к потенциометру по схеме, изображенной на рис. 96. Сопротивления вольтметров R1=6 кОм и R2 = 4кОм. Движок x стоит посередине потенциометра.

20 Три резистора включены по схеме, изображенной на рис. 97. Если резисторы включены в цепь в точках а и b, то сопротивление цепи будет R = 20 Ом, а если в точках а и с, то сопротивление цепи будет Rо = 15 Oм. Найти сопротивления резисторов R1, R2, R3, если R1=2R2.

Эквивалентные схемы включения изображены на рис. 350. Сопротивления реостатов

21 На сколько равных частей нужно разрезать проводник, имеющий сопротивление R = 36 Ом, сопротивление его частей, соединенных параллельно, было Ro — 1 Ом?

Весь проводник имеет сопротивление R = nr, где r-сопротивление каждой из п равных частей проводника. При параллельном соединении п одинаковых проводников их общее сопротивление R0 = r/n. Исключая r, получим

n может быть лишь целым положительным числом, большим единицы. Поэтому решения возможны только в случаях, когда R/Rо = 4, 9, 16, 25, 36,… В нашем случае

22 Из проволоки сделан каркас в форме куба (рис. 98), каждое ребро которого имеет сопротивление r. Найти сопротивление R этого каркаса, если ток I в общей цепи идет от вершины А к вершине В.

На участках Аа и bВ (рис. 351), ввиду равенства сопротивлений ребер куба и их одинакового включения, ток I равномерно разветвляется по трем ветвям и поэтому в каждой из них равен I/3. На участках ab ток равен I/6, так как в каждой точке а ток вновь разветвляется по двум ребрам с равными сопротивлениями и все эти ребра включены одинаково.

Напряжение между точками А и В складывается из напряжения на участке Аа, напряжения на участке ab и напряжения на участке bВ:

23 Из проволоки, единица длины которой имеет сопротивление Rl, сделан каркас в форме окружности радиуса r, пересеченной двумя взаимно перпендикулярными диаметрами (рис. 99). Найти сопротивление Rx каркаса, если источник тока подключен к точкам c и d.

Если источник тока подключен к точкам с и d, то напряжения на участках da и ab равны, поскольку проволока

однородна. Следовательно, разность потенциалов между точками а и b равна нулю. Ток на этом участке отсутствует. Поэтому наличие или отсутствие контакта в точке пересечения проводников ab и cd безразлично. Сопротивление Rx, таким образом, представляет собой сопротивление трех параллельно включенных проводников: cd с сопротивлением 2rR1, cad и cbd с одинаковыми сопротивлениями prR1. Из соотношения

24 Провод длины L=1 м сплетен из трех жил, каждая из которых представляет собой кусок неизолированной проволоки с сопротивлением единицы длины Rl = 0,02 Ом/м. На концах провода создано напряжение V=0,01 В. На какую величину DI изменится ток в этом проводе, если от одной жилы удалить кусок длины l=20 см?

25 Источник тока первоначально присоединяют к двум соседним вершинам проволочной рамки в форме правильного выпуклого n-угольника. Затем источник тока присоединяют к вершинам, расположенным через одну. При этом ток уменьшается в 1,5 раза. Найти число сторон n-угольника.

26 Как надо соединить четыре проводника с сопротивлениями R1 = 10м, R2 = 2 0м, R3 = 3 Ом и R4 = 4 0м, чтобы получить сопротивление R = 2,5 Ом?

Сопротивление R = 2,5 Ом достигается, когда проводники включены по схеме сметанного соединения (рис. 352).

27 Найти проводимость k цепи, состоящей из двух последовательных групп параллельно включенных проводников. Проводимости каждого проводника первой и второй групп равны k1=0,5Cм и k2 = 0,25 См. Первая группа состоит из четырех проводников, вторая- из двух.

28 Вольтметр рассчитан на измерение напряжений до максимального значения Vо = 30 В. При этом через вольтметр идет ток I=10 мА. Какое добавочное сопротивление Rд нужно присоединить к вольтметру, чтобы им можно было измерять напряжения до V=150В?

Для измерения вольтметром более высоких напряжений, чем те, на которые рассчитана шкала, необходимо включить последовательно с вольтметром добавочное сопротивление Rд (рис. 353). Напряжение на этом сопротивлении Vд=V-Vо; поэтому сопротивление Rд=(V-Vо)/I=12 кОм.

29 Стрелка миллиамперметра отклоняется до конца шкалы, если через миллиамперметр идет ток I=0,01 А. Сопротивление прибора R = 5 0м. Какое добавочное сопротивление Rд нужно присоединить к прибору, чтобы его можно было использовать в качестве вольтметра с пределом измерения напряжений V= 300 В?

Для измерения прибором напряжений, не превышающих V, необходимо последовательно с ним включить такое добавочное сопротивление Rд, чтобы V=I(R + Rд), где I-максимальный ток через прибор; отсюда Rд= V/I-R30 кОм.

30 Вольтметр, соединенный последовательно с сопротивлением R1 = 10 кОм, при включении в сеть с напряжением V=220 В показывает напряжение V1 = 70 В, а соединенный последовательно с сопротивлением R2, показывает напряжение V2 = 20 В. Найти сопротивление R2.

31 Вольтметр с сопротивлением R = 3 кОм, включенный в городскую осветительную сеть, показал напряжение V=125В. При включении вольтметра в сеть через сопротивление Ro его показание уменьшилось до Vо = 115 В. Найти это сопротивление.

Городская осветительная сеть представляет собой источник тока, обладающий внутренним сопротивлением, намного меньшим сопротивления вольтметра R. Поэтому напряжение V=125 В, которое показывал вольтметр при непосредственном включении в сеть, равно напряжению источника тока. Это значит, что оно не изменяется и при включении вольтметра в сеть через сопротивление Rо. Поэтому V=I(R + Rо), где I=Vо/R — ток, текущий через вольтметр; отсюда Rо = (V-Vо)R/Vо = 261 Ом.

32 Вольтметр с сопротивлением R = 50 кОм, подключенный к источнику тока вместе с добавочным сопротивлением Rд = 120 кОм, показывает напряжение Vо =100 В. Найти напряжение V источника тока.

Ток, текущий через вольтметр и добавочное сопротивление, I=Vо/R. Напряжение источника тока V=I(R+Rд)= (R+Rд)Vо/R = 340 В.

33 Найти показание вольтметра V с сопротивлением R в цепи, изображенной на рис. 100. Ток до разветвления равен I, сопротивления проводников R1 и R2 известны.

34 Имеется прибор с ценой деления i0=1 мкА/дел и числом делений шкалы N= 100. Сопротивление прибора R = 50 Ом. Как этот прибор приспособить для измерения токов до значения I=10 мА или напряжений до значения V= 1 В?

Для измерения более высоких токов чем те, на которые рассчитана шкала, параллельно прибору включается шунт с сопротивлением

для измерения напряжений последовательно с прибором включается добавочное сопротивление — ток, текущий через прибор при максимальном отклонении стрелки,

Напряжение на его клеммах в этом случае.

35 Миллиамперметр с пределом измерения токов I0 = 25 мА необходимо использовать как амперметр с пределом измерения токов I=5 А. Какое сопротивление Rш должен иметь шунт? Во сколько раз уменьшается чувствительность прибора? Сопротивление прибора R=10 Oм.

При включении параллельно прибору шунта (рис.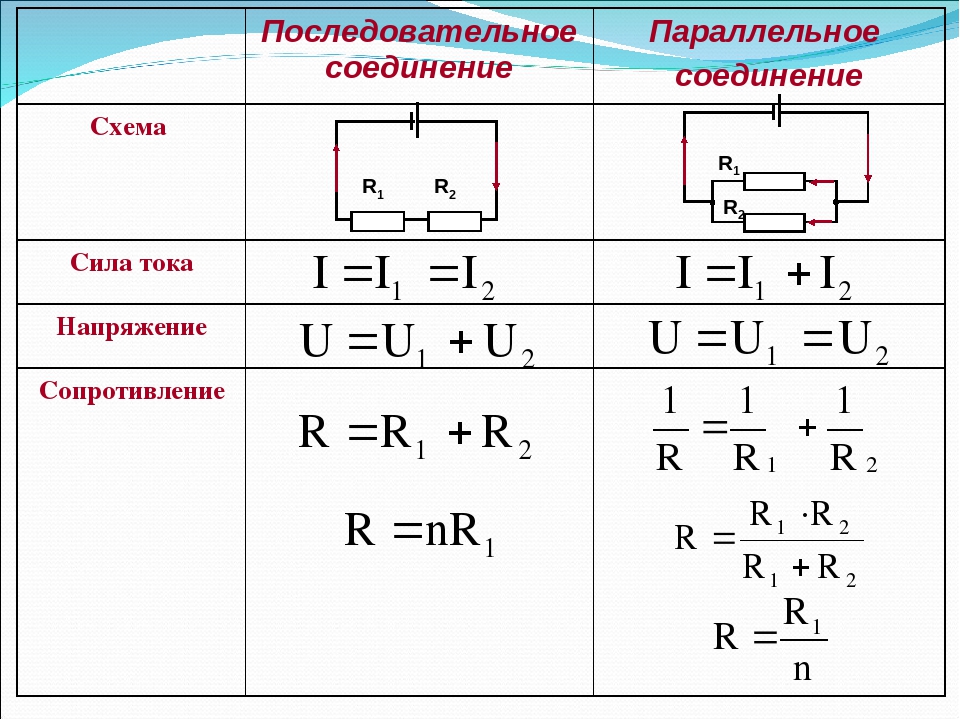 354) ток I должен делиться так, чтобы через миллиамперметр протекал ток Iо. Через шунт при этом течет ток Iш, т.е. I=Iо + Iш. Напряжения на шунте и на миллиамперметре равны: IоR = IшRш; отсюда

Rш=IоR/(I-Iо)0,05 Ом. Чувствительность прибора уменьшается, а цена деления прибора увеличивается в n=I/Iо=200 раз.

36 Амперметр с сопротивлением R = 0,2 Ом, накоротко присоединенный к источнику тока с напряжением V=1,5B, показывает ток I=5А. Какой ток I0 покажет амперметр, если его зашунтировать сопротивлением Rш=0,1 Ом?

37 При шунтировании гальванометра сопротивлениями R1, R2 и R3 в них ответвляется 90%, 99% и 99,9% тока I общей цепи. Найти эти сопротивления, если сопротивление гальванометра R = 27 Ом.

Так как шунты присоединяются к гальванометру параллельно, то условие равенства напряжений на гальванометре и на шунтах дает

38 Миллиамперметр с числом делений шкалы N=50 имеет цену деления i0 = 0,5 мА/дел и сопротивление R = 200 Ом. Как этот прибор приспособить для измерения токов до значения I= 1 А?

Наибольший ток, протекающий через прибор, Iо = iоN. Для измерения токов, значительно превышающих ток Iо, необходимо параллельно прибору включить шунт, сопротивление которого Rш значительно меньше сопротивления миллиамперметра R:

39 К амперметру с сопротивлением R = 0,1 Ом подключен шунт с сопротивлением Rш= 11,1 мОм. Найти ток, текущий через амперметр, если ток в общей цепи I=27 А.

Ток, текущий через шунт, Iш = I-Iо. Падения напряжения на шунте и амперметре равны: IшRш = IоR; отсюда Iо=IRш/(R+Rш) =2,7 А.

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U 1 + U 2 + U 3 или IR экв = IR 1 + IR 2 + IR 3 ,

откуда следует

R экв = R 1 + R 2 + R 3 .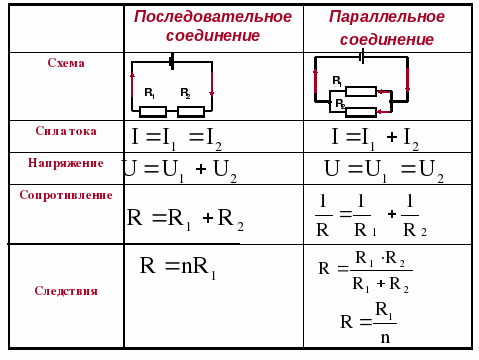

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

и по вышеприведенным формулам рассчитывают падение напряжений U 1 , U 2 , U 3 на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I 1 + I 2 + I 3 , т. е.

откуда следует, что

.

В том случае, когда параллельно включены два сопротивления R 1 и R 2 , они заменяются одним эквивалентным сопротивлением

.

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g экв = g 1 + g 2 + g 3 .

По мере роста числа параллельно включенных потребителей проводимость цепи g экв возрастает, и наоборот, общее сопротивление R экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

U = IR экв = I 1 R 1 = I 2 R 2 = I 3 R 3 .

Отсюда следует, что

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R. Сопротивления R 4 и R 5 включены параллельно, тогда сопротивление участка цепи cd равно:

.

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R 3 и R cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R 2 и R ad соединены параллельно, тогда сопротивление участка цепи аb равно

.

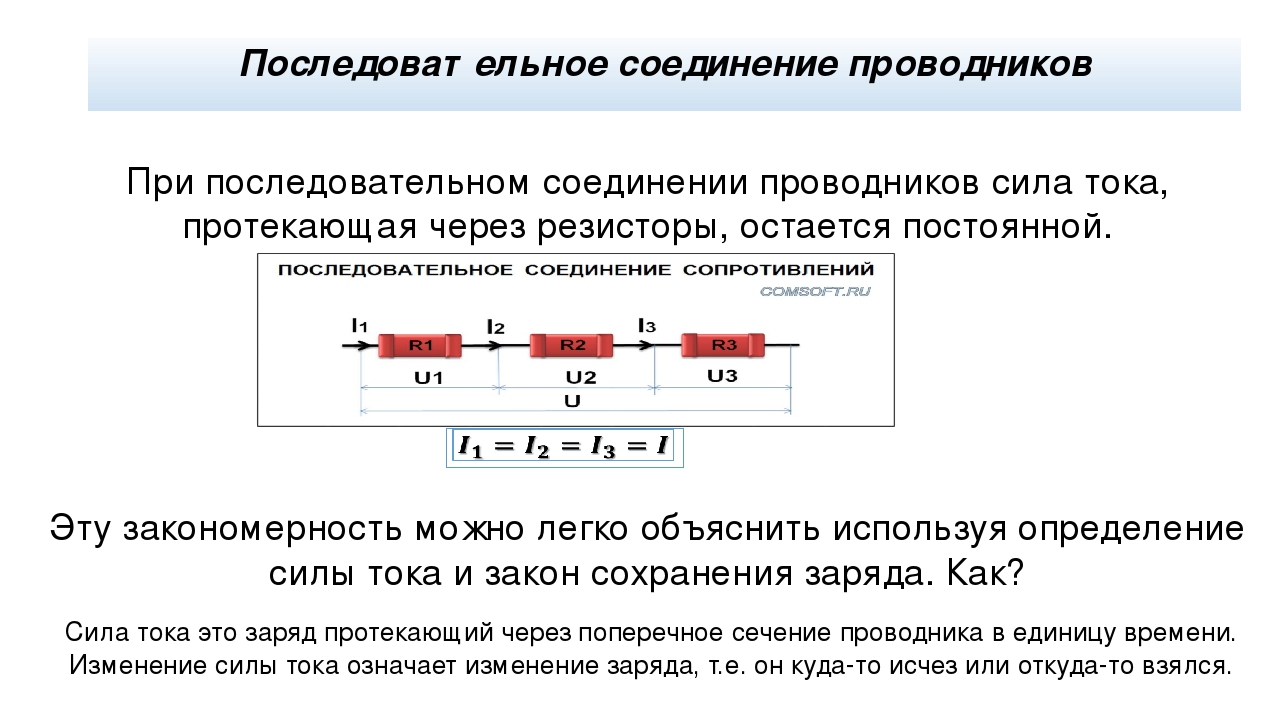
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R 1 и R ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.

Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока

Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.

Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б ).

Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е . Нагрузку подключают к генератору с помощью щеток 1 , прижимающихся к двум контактным кольцам 2 , которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В , размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v н :

e = Blv н (2. 1)

где В и l — постоянные величины, a v н — переменная, зависящая от угла α. Выразив скорость v н через линейную скорость катушки v , получим

e = Blv·sinα (2.2)

В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α .

Если угол α = π/2 , то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E m = Blv . Поэтому выражение (2.2) можно записать в виде

e = E m sinα (2.3)

Так как α есть угол поворота за время t , то, выразив его через угловую скорость ω , можно записать α = ωt , a формулу (2.3) переписать в виде

e = E m sinωt (2.4)

где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.

Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е , напряжений и и токов i справедливы законы постоянного тока.

Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е» .

Если число пар полюсов магнитов p ≠ 1 , то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,

f = Pn / 60

Из рис. 2.2 видно, что ωТ = 2π , откуда

ω = 2π / T = 2πf (2.5)

Величину ω , пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.

Графически изображенные на рис. 2.2 э. д. с. е и е» можно описать выражениями

e = E m sinωt; e» = E» m sin(ωt + ψ e» ) .

Здесь ωt и ωt + ψ e» — фазы, характеризующие значения э. д. с. e и e» в заданный момент времени; ψ e» — начальная фаза, определяющая значение э. д. с. е» при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ e = 0 ). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt ), а отрицательную фазу — вправо.

Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.

Разность углов φ , равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α . Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).

Когда для синусоидальных величин разность фаз равна ±π , то они противоположны по фазе, если же разность фаз равна ±π/2 , то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.

Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:

u = U m sin(ω t + ψ u ) ; i = I m sin(ω t + ψ i ) , (2.6)

причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ u — ψ i .

Уравнения (2.6) можно записать иначе:

u = U m sin(ωt + ψ i + φ) ; i = I m sin(ωt + ψ u — φ) ,

поскольку ψ u = ψ i + φ и ψ i = ψ u — φ .

Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ ).

Формы представления синусоидальных электрических величин.

Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.

1). Аналитическая форма представления

I = I m ·sin(ω·t + ψ i ), u = U m ·sin(ω·t + ψ u ), e = E m ·sin(ω·t + ψ e ),

где I , u , e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;

I m , U m , E m – амплитуды синусоидального тока, напряжения, ЭДС;

(ω·t + ψ ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;

ψ i , ψ u , ψ e – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0).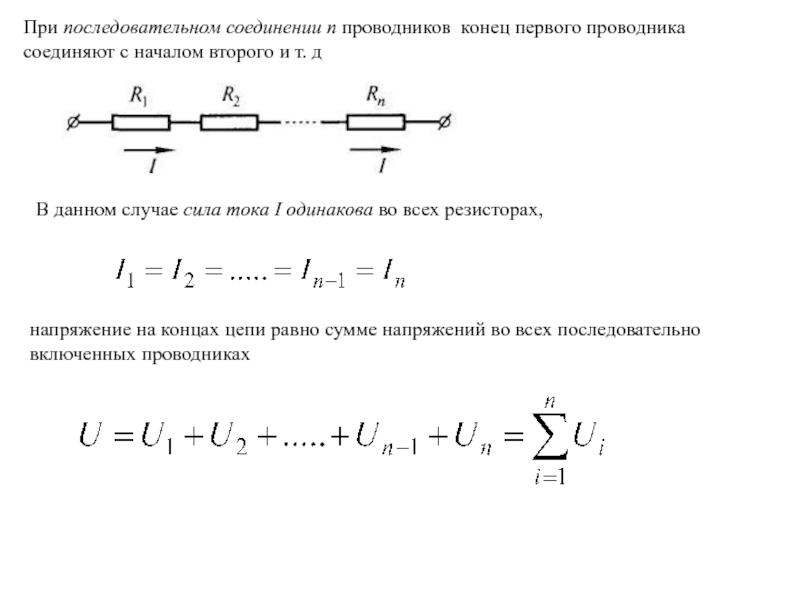 Начальная фаза может иметь как положительное так и отрицательное значение.

Графики мгновенных значений тока и напряжения показаны на рис. 2.3

Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ i φ . Сдвиг фаз между напряжением и током

φ = ψ u – ψ i = ψ u – (- ψ i) = ψ u + ψ i .

Применение аналитической формы для расчёта цепей является громоздкой и неудобной.

На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением

2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf . Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.

Рис. 2.4

Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4

3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.

Рис. 2.5

Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1 , ось ординат называют осью мнимых чисел и обозначают +j . (В некоторых учебниках ось действительных чисел обозначают Re , а ось мнимых – Im ). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:

а). Алгебраической

U = U ’+ jU «

I = I ’ – jI «,

где U «, U «, I «, I » – проекции векторов на оси действительных и мнимых чисел.

б). Показательной

где U , I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.

в). Тригонометрической

U = U ·(cosψ u + j sinψ u)

I = I ·(cosψ i – j sinψ i).

При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера

е j ·ψ = cosψ + j sinψ .

Неразветвлённые электрические цепи

Основы > Задачи и ответы > Постоянный электрический ток

Последовательное и параллельное соединения источников тока
Правило Кирхгофа

1 Найти разность потенциалов между точками а и b в схеме, изображенной на рис. 118. Э. д. с. источников тока e 1 = 1 В и e 2 =1,3 В, сопротивления резисторов R 1 = 10 Ом и R 2 = 5 Ом.
Решение:
Поскольку e 2 > e 1 то ток I будет идти в направлении, указанном на рис. 118, при этом разность потенциалов между точками а и b

2 Два элемента с э. д. с. e 1 = 1 ,5 B и e 2 r1 =0,6 Ом и r 2 = 0,4 Ом соединены по схеме, изображенной на рис. 119. Какую разность потенциалов между точками а и b покажет вольтметр, если сопротивление вольтметра велико по сравнению с внутренними сопротивлениями элементов?

Решение:
Поскольку e 2 > e 1 , то ток I будет идти в направлении, указанном на рис. 119. Током через вольтметр пренебрегаем ввиду
того, что его сопротивление велико по сравнению с внутренними сопротивлениями элементов. Падение напряжения на внутренних сопротивлениях элементов должно равняться разности э. д. с. элементов, так как они включены навстречу друг другу:
отсюда

Разность потенциалов между точками а и b (показание вольтметра)

3 Два элемента с э. д. с. e 1 =1.4B и e 2 = 1,1 В и внутренними сопротивлениями r =0,3 Ом и r 2 = 0,2 Ом замкнуты разноименными полюсами (рис. 120). Найти напряжение на зажимах элементов. При каких условиях разность потенциалов между точками а и b равна нулю?

Решение:

4 Два источника тока с одинаковыми э. д. с. e = 2 В и внутренними сопротивлениями r1 =0,4 Ом и r 2 = 0,2 Ом соединены последовательно. При каком внешнем сопротивлении цепи R напряжение на зажимах одного из источников будет равным нулю?

Решение:
Ток в цепи

(рис.361). Напряжения на зажимах источников тока

Решая первые два уравнения при условии V1=0, получим

Условие V2=0 неосуществимо, так как совместное решение первого и третьего уравнений приводит к значению R

5 Найти внутреннее сопротивление r1 первого элемента в схеме, изображенной на рис. 121, если напряжение на его зажимах равно нулю. Сопротивления резисторов R 1 = ЗОм, R 2 = 6 0м, внутреннее сопротивление второго элемента r 2 = 0,4 Ом, э. д. с. элементов одинаковы.

Решение:
Ток в общей цепи

По условию задачи напряжение на зажимах первого элемента

отсюда

6 При каком соотношении между сопротивлениями резисторов R 1 , R2, R3 и внутренними сопротивлениями элементов r1, r2 (рис. 122) напряжение на зажимах одного из элементов будет равно нулю? Э. д. с. элементов одинаковы.

Решение:

7 Два генератора с одинаковыми э. д. с. e = 6 В и внутренними сопротивлениями r1 =0,5 Ом и r2 = 0,38 Ом включены по схеме, изображенной на рис. 123. Сопротивления резисторов R 1 = 2 Ом, R2 = 4 Ом, R3 = 7 Ом. Найти напряжения V 1 и V2 на зажимах генераторов.

Решение:
Ток в общей цепи

где внешнее сопротивление цепи

Напряжения на зажимах первого и второго генератора
напряжение на зажимах второго генератора

8 Три элемента с э. д. с. e 1 = 2,2 В, e 2 = 1 ,1 В и e 3 = 0,9 В и внутренними сопротивлениями r 1 = 0,2 Ом, r 2 = 0,4 Ом и r з = 0,5 Ом включены в цепь последовательно. Внешнее сопротивление цепи R= 1 Ом. Найти напряжение на зажимах каждого элемента.

Решение:
По закону Ома для полной цепи ток

Напряжение на зажимах каждого элемента равно разности э. д. с. и падения напряжения на внутреннем сопротивлении элемента:


Напряжение на зажимах батареи элементов равно падению напряжения на внешнем сопротивлении цепи:

Напряжение на зажимах третьего элемента оказалось отрицательным, так как ток определяется всеми сопротивлениями цепи и суммарной э.д.с, а падение напряжения на внутреннем сопротивлении r3 больше, чем э.д.с. e 3 .

9 Батарея из четырех последовательно включенных в цепь элементов с э. д. с. e = 1,25 В и внутренним сопротивлением r = 0,1 Ом питает два параллельно соединенных проводника с сопротивлениями R1 = 50 Ом и R 2 = 200 Ом. Найти напряжение на зажимах батареи.

Решение:

10 Сколько одинаковых аккумуляторов с э. д. с. e = 1 ,25B и внутренним сопротивлением r = 0,004 Ом нужно взять, чтобы составить батарею, которая давала бы на зажимах напряжение V= 11 5 В при токе I =25 А?

Решение:
Напряжение на зажимах батареи

Следовательно,

11 Батарея из n = 40 последовательно включенных в цепь аккумуляторов с э. д. с. e = 2,5 В и внутренним сопротивлением r = 0,2 Ом заряжается от сети с напряжением V=121 В. Найти зарядный ток, если последовательно в цепь введен проводник с сопротивлением R = 2 Ом.

Решение:

12 Два элемента с э. д. с. e 1 = 1,25 В и e 2 = 1,5 В и одинаковыми внутренними сопротивлениями r = 0,4 Ом соединены параллельно (рис. 124). Сопротивление резистора R = 10 Ом. Найти токи, текущие через резистор и каждый элемент.

Решение:
Падение напряжения на резисторе, если токи текут в направлениях, указанных на рис. 124,

Учитывая, что I=I1+I2, находим

Заметим, что I1
13 Два элемента с э. д. с. e 1 =6 В и e 2 = 5 В и внутренними сопротивлениями r1 = 1 Ом и r2 = 20м соединены по схеме, изображенной на рис. 125. Найти ток, текущий через резистор с сопротивлением R = 10 Ом.

Решение:
Выбрав направления токов, указанные на рис. 362, составим уравнения Кирхгофа. Для узла b имеем I1+I2-I=0; для контура abef (обход по часовой стрелке)

и для контура bcde (обход против часовой стрелки)

Из этих уравнений найдем

14 Три одинаковых элемента с э. д. с. e = 1,6 В и внутренним сопротивлением r =0,8 Ом включены в цепь по схеме, изображенной на рис. 126. Миллиамперметр показывает ток I =100 мА. Сопротивления резисторов R 1 = 10Ом и R2 = 15 0м, сопротивление резистора R неизвестно. Какое напряжение V показывает вольтметр? Сопротивление вольтметра очень велико, сопротивление миллиамперметра пренебрежимо мало.

Решение:
Внутреннее сопротивление элементов

Сопротивление параллельно включенных резисторов

Общая э. д. с. элементов e 0 =2 e Согласно закону Ома для полной цепи

15 Сопротивления резисторов R 1 и R 2 и э. д. с. e 1 и e 2 источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. e 3 третьего источника ток через резистор R3 не течет?

Решение:
Выберем направления токов I1, I2 и I3 через резисторы R1, R2 и R3, указанные на рис. 363. Тогда I3=I1+I2. Разность потенциалов между точками а и b будет равна

Если

Исключая I1 находим

16 Цепь из трех одинаковых последовательно соединенных элементов с э.д.с. e и внутренним сопротивлением r замкнута накоротко (рис. 128). Какое напряжение покажет вольтметр, подключенный к зажимам одного из элементов?

Решение:
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим

Из закона Ома для участка цепи между точками а и b получим

Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
17 Источник тока с э.д.с. e 0 включен в схему, параметры которой даны на рис. 129. Найти э.д.с. e источника тока и направление его подключения к выводам а и b , при которых ток через резистор с сопротивлением R2 не идет.

Решение:
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I0+I2. При обходе контуров aefb и ecdf по часовой стрелке получим
Используя условие I2 = 0, находим

Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18 Два элемента с одинаковыми э.д.с. e включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента равно 2/3. Найти внутренние сопротивления элементов r1 и r 2, если r 1=2 r 2.

Решение:

19 Два одинаковых элемента с э.д.с. e = 1 ,5 В и внутренним сопротивлением r = 0,2 Ом замкнуты на резистор, сопротивление которого составляет в одном случае R1=0,2 Oм, В другом — R 2 = 20 Ом. Как нужно соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?

Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и e при последовательном соединении они равны 2r и 2 e . Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+rr. Поэтому ток больше при последовательном соединении.
20 Два элемента с э.д.с. e 1 =4В и e 2 = 2В и внутренними сопротивлениями r1 = 0,25 Ом и r 2 = 0,75 Ом включены в схему, изображенную на рис. 130. Сопротивления резисторов R1 = 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.

Решение:

21 К батарее из двух параллельно включенных элементов с э.д.с. e 1 и e 2 и внутренними сопротивлениями r1 и r 2 подключен резистор с сопротивлением R. Найти ток I , текущий через резистор R, и токи I1 и I 2 в первом и втором элементах. При каких условиях токи в отдельных цепях могут быть равными нулю или изменять свое направление на обратное?

Решение:
Выберем направления токов, указанные на рис. 366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим

Из этих уравнений находим

Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие

Ток I1=0 при

а ток I2 = 0 при

Токи I1 и I2 имеют направления, указанные на рис.366, если

Они меняют свое направление при

22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом- параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?

Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R № r, задача не имеет решения (n =1).
23 Батарея из n = 4 одинаковых элементов с внутренним сопротивлением r =2 Ом, соединенных в одном случае последовательно, в другом — параллельно, замыкается на резистор с сопротивлением R =10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с R и r.

Решение:

где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24 Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если n =10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э.д.с. элемента e = 2 В, его внутреннее сопротивление r = 0,2 Ом.

Решение:

25 Батарея составлена из N=600 одинаковых элементов так, что п групп соединены последовательно и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента e = 2 В, его внутреннее сопротивление r = 0,4 Ом. При каких значениях n и m батарея, будучи замкнута на внешнее сопротивление R = 0,6 Ом, отдаст во внешнюю цепь максимальную мощность? Найти при этом ток, текущий через сопротивление R.

Решение:
Общее число элементов N=nm (рис. 367). Ток во внешней цепи

где r/ m — внутреннее сопротивление группы из т параллельно соединенных элементов, а n r/ m — внутреннее сопротивление n групп, соединенных последовательно. Максимальная мощность (см. задачу 848) отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов n r/ m , т. е.
При этом через сопротивление R течет точек I=46 А.

26 Емкость аккумулятора =80 А Ч ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.

Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора:
При параллельном соединении n аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в n раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:

Заметим, однако, что энергия

отдаваемая батареей в цепь, и при последовательном и при параллельном соединении n аккумуляторов в n раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в n раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.
27 Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора Qo =64 А Ч ч .

Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость

Три параллельно включенные группы дают общую емкость батареи

28 Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви I =0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.

Решение:

29 Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока e 1 = 6,5 В и e 2 = 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.

Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом

Для контура abfg (обход по часовой стрелке),

Для контура bcdh (обход против часовой стрелки) и

для контура hdef (обход по часовой
стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим

Отрицательные значения токов I2, I4 и I6 показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.

Сила тока при последовательном соединении

В электрических цепях используются различные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае используется несколько сопротивлений, соединенных в единую цепочку друг за другом. То есть, начало одного резистора соединяется с концом второго, а начало второго – с концом третьего и так далее, до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.

Последовательное и параллельное соединение сопротивлений

Любая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока. Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.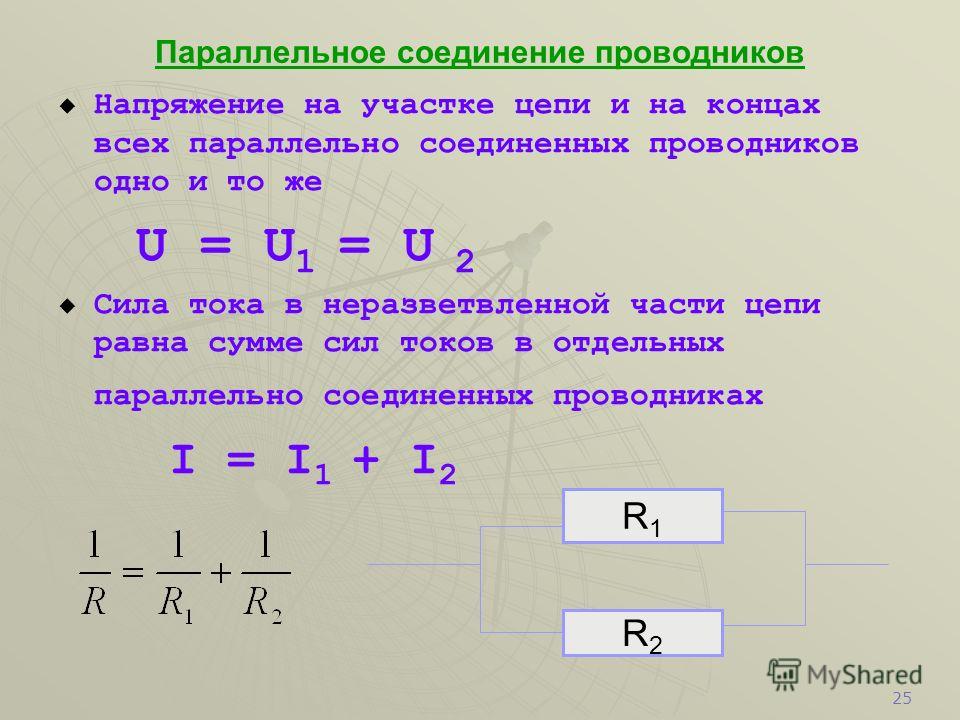

В большинстве электрических цепей применяются медные проводники. Каждая цепь содержит приемники энергии – нагрузки, обладающие различными сопротивлениями. Параметры соединения лучше всего рассматривать на примере внешней цепи источника тока, состоящей из трех резисторов R1, R2, R3. Последовательное соединение предполагает поочередное включение этих элементов в замкнутую цепь. То есть начало R1 соединяется с концом R2, а начало R2 – с концом R3 и так далее. В такой цепочке может быть любое количество резисторов. Эти символы используют в расчетах последовательные и параллельные соединения.

Сила тока на всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается лишь определить, каким будет напряжение при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.

При постоянном значении напряжения, ток при последовательном соединении будет находиться в зависимости от сопротивления цепи. Поэтому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Кроме того, изменятся ток и напряжение на каждой нагрузке. Основным недостатком последовательного соединения считается прекращение работы всех элементов цепи, при выходе из строя даже одного из них.

Совершенно другие характеристики тока, напряжения и сопротивления получаются при использовании параллельного соединения. В этом случае начала и концы нагрузок соединяются в двух общих точках. Происходит своеобразное разветвление тока, что приводит к снижению общего сопротивления и росту общей проводимости электрической цепи.

Для того чтобы отобразить эти свойства, вновь понадобится закон Ома. В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все характеристики отображаются следующим образом: сила тока – I = I1 + I2 + I3, напряжение – U = U1 = U2 = U3, сопротивление – 1/R = 1/R1 + 1/R2 + 1/R3.

При неизменном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один или несколько резисторов будут выключены из цепи, это никак не повлияет на работу других устройств, остающихся включенными. Данный фактор является основным преимуществом параллельного соединения электроприборов.

В схемах обычно не используется только последовательное соединение и параллельное соединение сопротивлений, они применяются в комбинированном виде, известном как смешанное соединение. Для вычисления характеристик таких цепей применяются формулы обоих вариантов.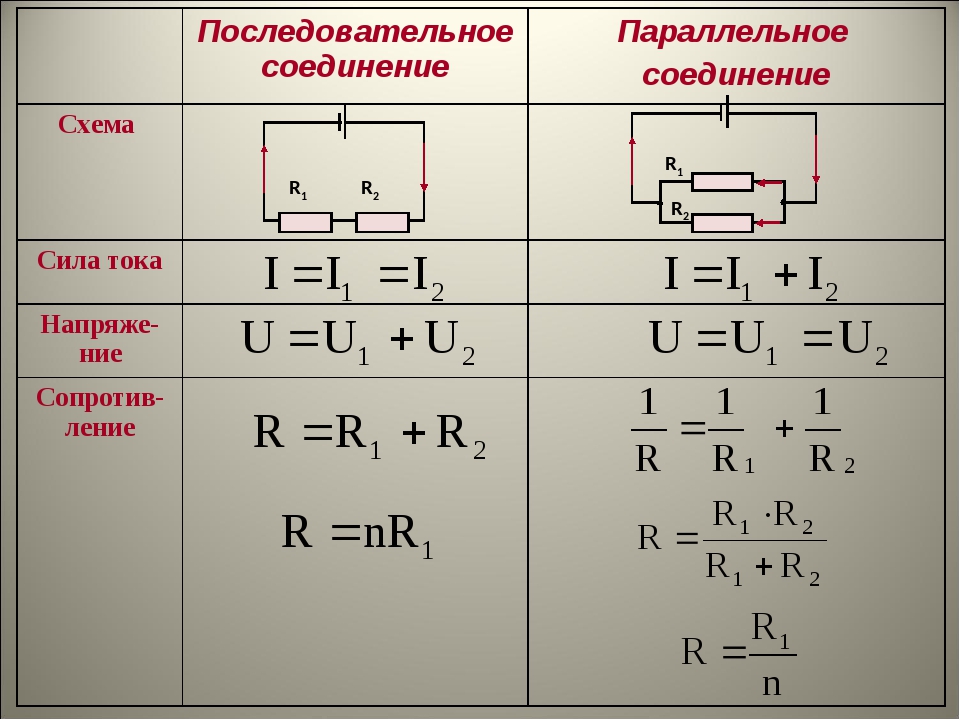 Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.

Законы последовательного и параллельного соединения проводников

Основным законом, применяемым при расчетах различных видов соединений, является закон Ома. Его основным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и обратно пропорциональной сопротивлению на данном участке. В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.

Более сложные вычисления с участием других величин требуют применения правила Кирхгофа. Его основное положение заключается в том, что несколько последовательно соединенных источников тока, будут обладать электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них. Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.

В том случае, когда ЭДС источников будет иметь разное значение, для расчетов силы тока на различных участках цепи применяются дополнительные правила Кирхгофа.

Последовательное соединение проводников — Технарь

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного проводника (или приемника электрического тока), а из нескольких различных проводников, которые могут быть соединены между собой по-разному.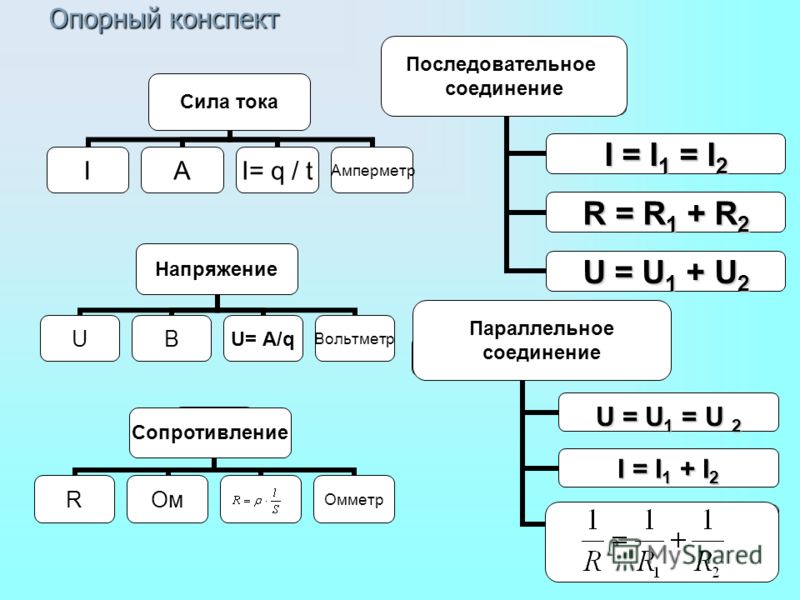 Зная сопротивление каждого из проводников и способ их соединения, можно рассчитать общее сопротивление цепи.

На рисунке 266, а изображена цепь последовательного соединения двух электрических ламп, а на рисунке 266, б — схема такого соединения. Если выключить одну лампу, то день разомкнется и другая лампа погаснет.

С последовательным соединением мы встречались в предыдущих параграфах. Так, последовательно соединены аккумулятор, лампа, два амперметра и ключ в цепи, изображенной на рисунке 249. Мы уже знаем, что при последовательном соединении проводников сила тока в любых частях цепи одна и та же.

А чему равно сопротивление последовательно соединенных проводников?

Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника. Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):

R = R1 + R2

Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:

U1 = IR1, U2 = IR2

Отсюда видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.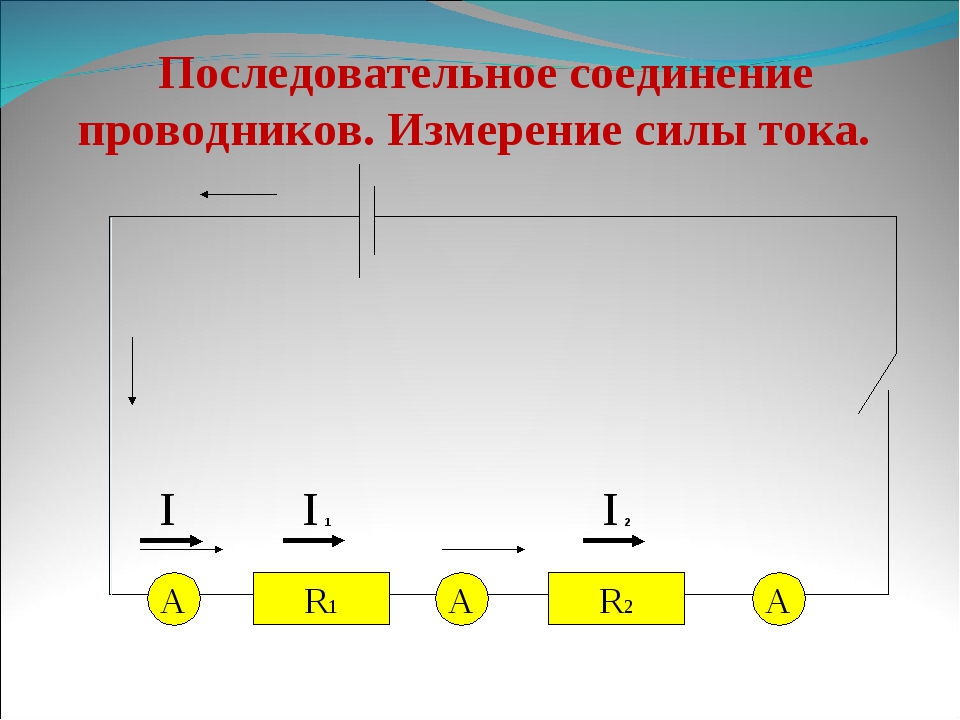 Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:

U = U1 + U2

Пример. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Вопросы. 1. Какое соединение проводников называют последовательным? Изобразите его на схеме. 2. Какая из электрических величин одинакова для всех проводников, соединенных последовательно? 3. Как найти общее сопротивление цепи, зная сопротивление отдельных проводников при последовательном их соединении? 4. Как найти напряжение участка цепи, состоявшего из двух последовательно соединенных проводников, зная напряжение на каждом из них?

Упражнения. 1. Цепь состоит из двух последовательно соединенных проводников, 02 сопротивление которых 4 и 6 Ом.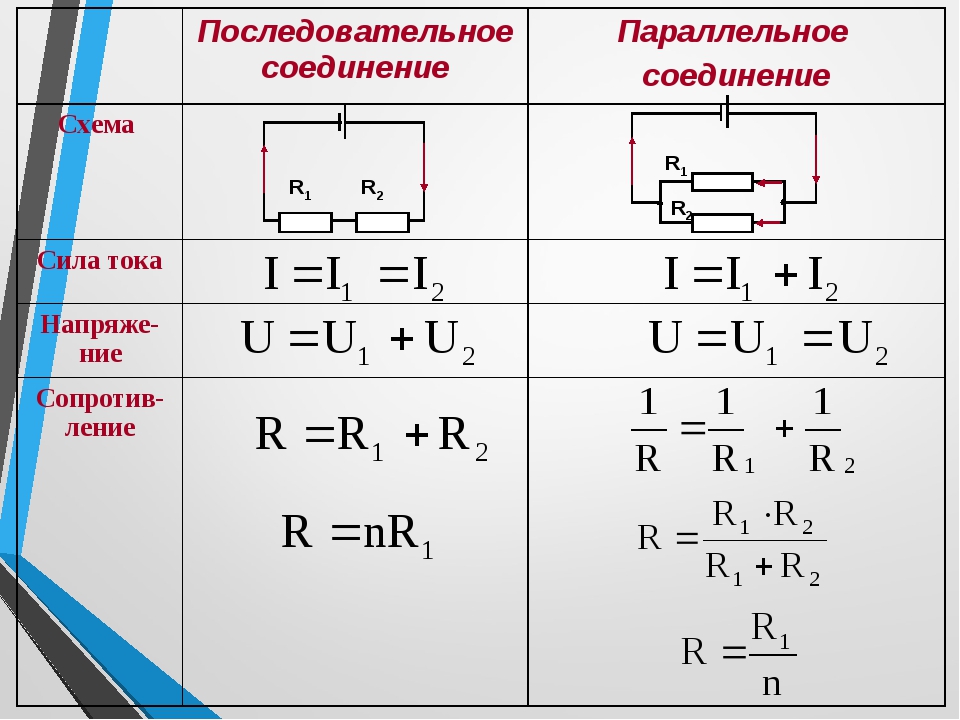 Сила тока в цепи 0,2 А. Найдите напряжение на каждом из проводников и общее напряжение. 2. Для электропоездов применяют напряжение 1200 В. Как можно использовать для освещения вагонов лампы, рассчитанные на напряжение 220 В каждая? Начертите схему включения ламп. 3. Две одинаковые лампы, рассчитанные на 127 В каждая, соединены последовательно и включены в сеть с напряжением 127 В. Под каким напряжением будет находиться каждая лампа?

Параллельное и последовательное соединение проводников. — Объяснение нового материала.

Комментарии преподавателя

Последовательное соединение проводников

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приёмника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.

На рисунке а изображена цепь последовательного соединения двух электрических ламп, а на рисунке б — схема такого соединения.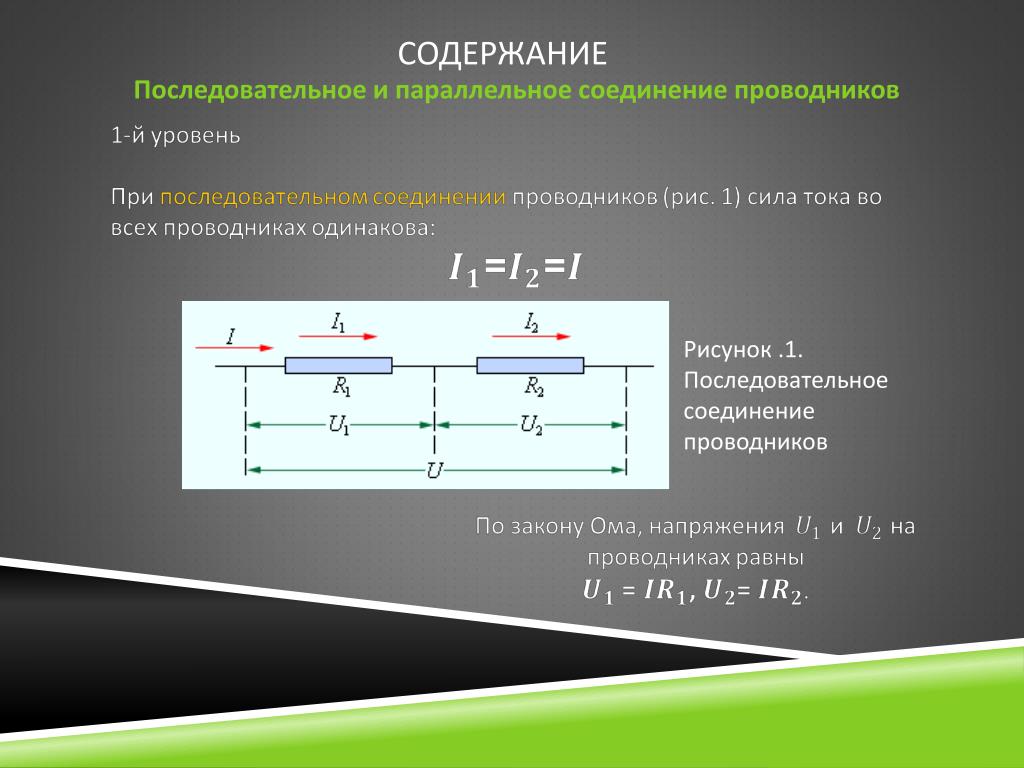 Если выключать одну лампу, то цепь разомкнётся и другая лампа погаснет.

Рис. Последовательное включение лампочек и источников питания

Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.

I = I1 = I2

А чему равно сопротивление последовательно соединённых проводников?

Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.

Последовательное соединение проводников

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):

R = R1 + R2

Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:

U1 = IR1, U2 = IR2.

Из приведённых равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.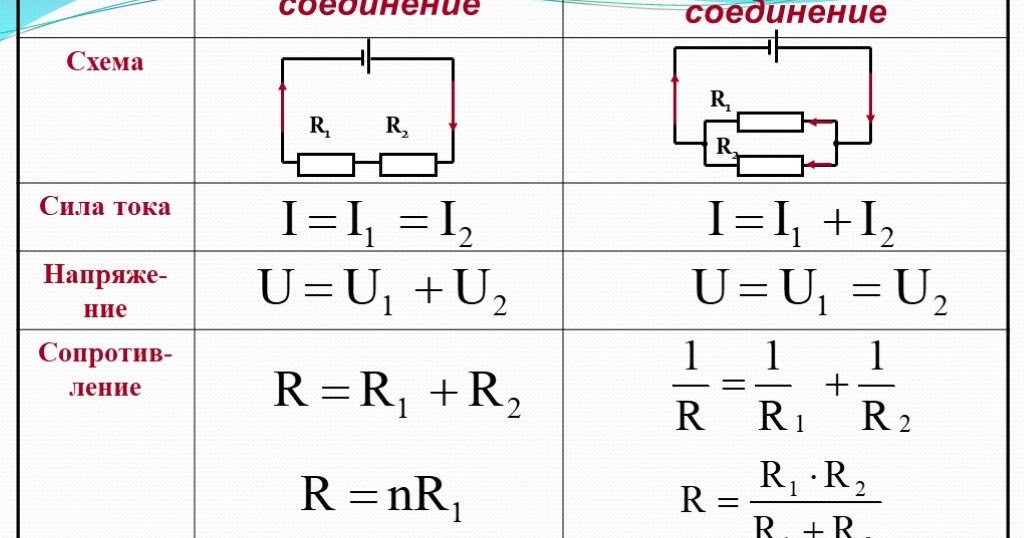

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:

U = U1 + U2.

Это равенство вытекает из закона сохранения энергии. Электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по участку цепи электрического заряда в 1 Кл. Эта работа совершается за счёт энергии электрического поля, и энергия, израсходованная на всём участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.

Все приведённые закономерности справедливы для любого числа последовательно соединённых проводников.

Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.

Запишем условие задачи и решим её.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ

 

Расчет параметров электрической цепи
при параллельном соединении сопротивлений:

1. сила тока в неразветвленном участке цепи равна сумме сил токов
во всех параллельно соединенных участках

2. напряжение на всех параллельно соединенных участках цепи одинаково

3. при параллельном соединении сопротивлений складываются величины, обратные сопротивлению :

( R — сопротивление проводника,
1/R — электрическая проводимость проводника)

Если в цепь включены параллельно только два сопротивления, то:

( при параллельном соединении общее сопротивление цепи меньше меньшего из включенных сопротивлений )

4. работа электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме работ на отдельных участках:

A=A1+A2

5. мощность электрического тока в цепи, состоящей из параллельно соединенных участков,
равна сумме мощностей на отдельных участках:

P=P1+P2

Для двух сопротивлений:

т.е. чем больше сопротивление, тем меньше в нём сила тока.

 

Использованные источники:

• http://www.tepka.ru/fizika_8, http://class-fizika.narod.ru
• https://www.youtube.com/watch?v=AW3n2XP4CQE
• https://www.youtube.com/watch?v=Bo1UwoBicew

 

Файлы

Нет дополнительных материалов для этого занятия.

Параллельное включение полупроводниковых приборов

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R.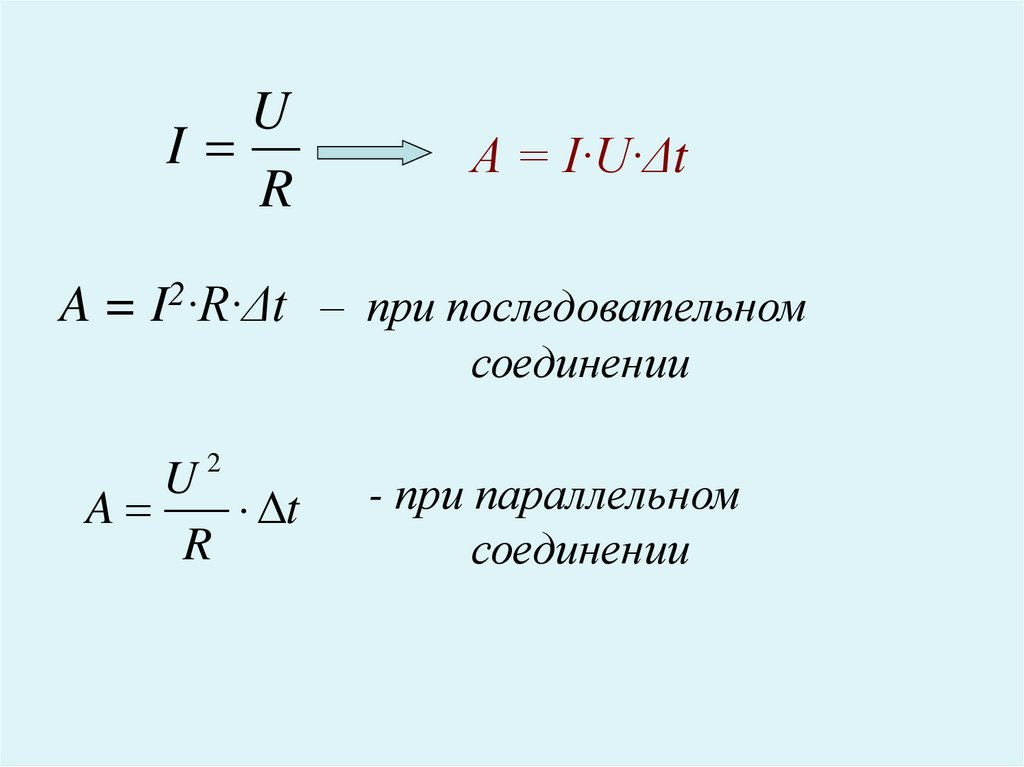 В результате получаем, что

I₁ = U/R₁

I₂ = U/R₂

I₃ = U/R₃

Если бы у нас еще были резисторы, соединенные параллельно, то для них

I_n = U/R_n

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.

I₁ = U/R₁

I₂ = U/R₂

I₃ = U/R₃

Если бы у нас еще были резисторы, соединенные параллельно, то для них

I_n = U/R_n

Следовательно,

I₁ = U/R₁ = 10/2=5 Ампер

I₂ = U/R₂ = 10/5=2 Ампера

I₃ = U/R₃ = 10/10=1 Ампер

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

I=I₁ + I₂ + I₃ = 5+2+1=8 Ампер

2-ой способ найти I

I=U/R_общее

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

I=U/R_общее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Последовательное соединение — диод

Последовательное соединение диодов без их шунтирования возможно при условии соединения диодов только одной группы, подобранной по величине наибольшего обратною тока.
 

Последовательное соединение диодов используется очень часто. Однако с дальнейшим увеличением ( / обр цены за каждый отдельно взятый диод заметно возрастают. В находится в пределах 10 дол.
 

Последовательное соединение диодов может производиться без специального подбора, если диоды шунтированы сопротивлениями.
 

Последовательное соединение диодов не допускается.
 

Допускается последовательное соединение диодов при условии шунтирования каждого диода резистором сопротивлением 100 кОм на каждые 100 В.
 

Допускается последовательное соединение диодов одного типономинала при условии обеспечения на каждом диоде значения максимально допустимого обратного напряжения для данного типономинала.
 

Допускается последовательное соединение одинаковых диодов для увеличения допустимого обратного напряжения и параллельное — для увеличения допустимого выпрямляемого тока. При последовательном соединении диодов обратное напряжение будет распределяться не равномерно, а пропорционально обратным сопротивлениям диодов, которые могут существенно отличаться по величине. Для выравнивания распределения напряжения на диодах параллельно каждому диоду включают сопротивление порядка 0 1 — н — т — 0 5 Мом. При параллельном включении диодов для исключения неравномерности нагрузки в них последовательно с каждым из них включают выравнивающее сопротивление в 10 — ь 50 ом.
 

При последовательном соединении диодов рекомендуется шунтировать диод резистором с сопротивлением 10 — 15 кОм на каждые 100 В амплитуды обратного напряжения.
 

При последовательном соединении диодов с целью увеличения выпрямленного напряжения рекомендуется применять диоды одного типа и шунтировать каждый прибор сопротивлением 10 — 15 кОм на каждые 100 В амплитуды обратного напряжения.
 

При последовательном соединении диодов с целью увеличения выпрямленного напряжения рекомендуется применять диоды одного типа и шунтировать каждый диод сопротивлением 10 — 15 кОм на каждые 100 В амплитуды обратного напряжения.
 

При последовательном соединении диодов с целью увеличения выпрямленного напряжения рекомендуется применять диоды одного типа и шунтировать каждый диод сопротивлением 10 — IS кОм на каждые 100 В амплитуды обратного напряжения.
 

При последовательном соединении диодов или тиристоров вследствие неодновременного окончания протекания обратного тока напряжение между вентилями не распределяется равномерно и воздействие перенапряжений на отдельные вентили усиливается.
 

При последовательном соединении диодов рекомендуется шунтировать диод резистором с сопротивлением 10 — 15 кОм на каждые 100 В амплитуды обратного напряжения.
 

При последовательном соединении диодов рекомендуется шунтировать диод резистором с сопротивлением 10 — 15 кОм на каждые 100 В амплитуды обратного напряжения.
 

При последовательном соединении диодов рекомендуется шунтировать диод резистором с сопротивлением 10 — 15 кОм на каждые 100 В амплитуды обратного напряжения.
 

Принципы подключения

Светоизлучающие диоды активно применяются в подсветке, индикации

Своими руками можно создать устройства, поэтому важно знать, как производить соединение светодиодов

К основным способам подключения относятся:

• параллельное;
• последовательное;
• комбинированное.

Основные причины выхода из строя светодиодных цепочек:

• неправильное соединение;
• некачественные диоды или блоки питания.

Конструкция излучающего диода подразумевает его подключение к источнику постоянного тока

При соединении важно соблюдать полярность компонента – если перепутать катод и анод, диод не будет излучать световой поток

Полярность

Определить, какой из электродов является плюсом, а какой – минусом, можно несколькими способами.

Первый – конструктивно. Обычный LED компонент имеет две ножки, длинная является плюсом (анодом), а короткая – катодом.

При помощи тестера. Для этого нужно взять мультиметр, перевести его в положение «Прозвонка» и прикладывать щупы к электродам. Когда красный щуп коснется анода, а черный катода – светодиод загорится. Если при перестановке на шкале высвечивается и не меняется «бесконечное» сопротивление, есть неполадка с элементом. Так что мультитестер используется и для проверки работоспособности излучающих приборов.

Визуальный осмотр. Можно посмотреть внутрь колбы. Широкая часть – это катод, а узкая – анод. Мощные светодиоды сверхъяркого типа имеют маркировку выводов «+» и «–». Компоненты для поверхностного монтажа обычно имеют специальный скос, который указывает на катод.

Включение в источник питания. Диод можно подключить к аккумулятору, батарее или другому блоку. Нужно постепенно повышать электропитание, которое вызовет свечение. Если компонент не горит, полярность следует поменять. Собирается такая схема проверки обязательно с использованием токоограничивающего резистора.

По технической документации. В паспорте прибора будет написано, какая полярность.

После определения плюса и минуса электродов нужно разобраться с методом подсоединения.

Какие светодиоды можно подключить к 12 Вольтам

Продавцы уверяют, что продают светодиоды, которые возможно подключить к источнику питания на 12 В. На самом деле это утверждение некорректно. У лед-лампочки нет строго определенного рабочего вольтажа, поэтому можно говорить только об источнике света, изготовленном из диодов.

Следует определить, что происходит в лед-лампочке во время свечения. В данном процессе самые важные 2 параметра: максимальный и рабочий (необходимый для свечения) ток. Они учитываются в производстве лед-матриц, но не при выборе источника тока.

Напряжение на лампочке чаще всего от 1,5 до 3,5 вольт, цифра зависит от цвета лампочки. Меньшее значение – красные диоды, самое большое – сверхяркие. Светящийся диод на 12 вольт – это матрица (сборка), в состав которой может входить любое количество кристаллов, соединенных последовательно. Подобных цепочек может быть несколько, они соединяются друг с другом параллельно.

Параллельное соединение резисторов онлайн калькулятор

Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться

Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

Для этого вам необходимо:

• Указать в графе “количество резисторов” их число, в нашем примере их три;
• После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
• Далее нажмите кнопку “рассчитать” и в окошке “параллельное сопротивление в цепи” вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку “сбросить”, чтобы обнулить значение параллельно включенных элементов калькулятора.

  Подключение магнитного пускателя через кнопочный пост видео

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

• Rсум – суммарное сопротивление параллельно соединенных элементов
• R1 – сопротивление первого резистора;
• R2 – сопротивление второго резистора;
• R3 – сопротивление третьего резистора;
• Rn – сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах

Онлайн калькулятор для расчета параллельного сопротивления позволит установить общее эквивалентное сопротивление в цепи R1 + R2 +Rn. Данный калькулятор можно смело назвать одним из самых простых и эффективных.

  Литейная машина под давлением

Для получения результатов вам необходимо ввести:

• Количество резисторов.
• Указать мощность каждого резистора (Ом).
• Нажать кнопку «Расчитать».

В результате вы сможете получить точно сопротивление резисторов в сети

Калькулятор для расчета параллельного сопротивления позволит безошибочно все определить, а это очень важно, так как ручной расчет считается достаточно сложным и трудоемким процессом. Наш калькулятор с легкостью поможет вам справиться со всем

Для того чтобы определить общее эквивалентное сопротивление, можно воспользоваться точным и удобным калькулятором. Где, внеся данные по количеству резисторов, калькулятор произведет расчет в автоматическом режиме.

Данное соединение является одним из 2-ух видов, в данном случае оба вывода 1-го из резисторов соединяются с выводами 2-го резистора. В иных случаях их принято соединять параллельно или последовательно, чтобы можно было создать схемы сложного типа.

  Многофункциональный станок своими руками чертежи

Для того чтобы найти ток, который протекает через определенный резистор, следует использовать формулу: Произведем расчеты согласно примеру Разрабатывается устройство, в котором есть необходимость использовать резистор, которое имеет сопротивление 8Ом. Исходя из того, что номинальный ряд согласно стандартным значениям таких резисторов не имеет, выходом будет использование 2-ух резисторов соединенных параллельно.

Для такого способа производятся следующие расчеты: Данная формула показывает, что в случае когда R1 = R2, R будет составлять ровно половину сопротивления 1-го из 2-ух резисторов. И если R=8Ом, то соответственно R1 и R2 = 2*8=16Ом.

Предложения и пожелания пишите на [email protected]

Поделитесь этим калькулятором на форуме или в сети!

Это помогает делать новые калькуляторы.

Параллельное подключение светодиодов

Здесь у нас всё наоборот. Силу тока нужно умножить на количество светодиодов, а падение напряжения посчитать только 1 раз.
Сила тока: I = 0,025 * 15 =0,375 А
Нам потребуется источник питания, способный выдать максимальный ток в 0,375 А. Округлим до 0,35 (помните, что лучше «недолить»?). По напряжению тоже укладываемся: 12 — 2 = 10. Остаётся с большим запасом.

Пытливый читатель, запнувшийся парой абзацев ранее, может воскликнуть: «Погодите! Так зачем нам 12 вольт, если мы можем обойтись и пятью?». «Можем!» — ответим ему мы. Но не торопитесь с выводами, это ещё не конец.

Мы определились, что светодиоды будут подключены параллельно. Необходимо ограничить ток в цепи. Допустим, специального драйвера у нас нет. Возьмём резистор. Рассчитаем необходимое сопротивление по давно известной формуле: 12 В * 0,35 А = 4,2 Ом. Подключим его между источником питания и анодами светодиодов:

Неправильное параллельное подключение трёх светодиодов

Вот, казалось бы, и всё. Но есть проблема:

ТАК ДЕЛАТЬ НЕЛЬЗЯ!!!

Как отмечалось выше, светодиоды не обязательно имеют те характеристики, которые заявлены производителем. Всегда есть разброс. И вот мы задали ток в 0,35 ампер и смотрим на светящуюся линейку светодиодов. Но всем им нужен разный ток. Одному , как мы и рассчитывали 25мА, другому — 20мА, третьему 21мА, а вот нашёлся совсем кривой светодиод, ему нужно всего 15мА. А мы пропускаем через него 25 — почти в 2 раза больше. Светодиод греется и быстро перегорает. В линейке стало на 1 светодиод меньше. Теперь для питания оставшихся светодиодов нам требуется 35мА. Пока всё не выглядит особенно плохо. Мы ограничили ток с запасом. Мы молодцы. Но не выдержал ещё один светодиод. Осталось 13. Теперь весь наш ток делится не на 15, а на 13 светодиодов. На каждый из них приходится по 26мА. Теперь абсолютно все светодиоды работают на повышенном токе. Очень скоро перегреется следующий. Самые стойкие получат уже по 29мА — 116% от номинала. Всего 2 перегоревших светодиода запустили цепную реакцию. Скоро вся линейка перегорит, а вы так и не поймёте почему (ну или поймёте, мы же только что всё разобрали). Собственно, избавиться от такого печального сценария просто. Нужно к каждому светодиоду поставить по собственному токоограничительному резистору. Для тока в 25мА и напряжения 12В нужен резистор на 480 Ом. Это не спасёт от проблемы «кривых» светодиодов, но их перегорание никак не повлияет на остальные.

Достоинства: высочайшая надёжность.Недостатки: высокое потребление тока, высокая стоимость схемы.

Правильное параллельное подключение трёх светодиодов

Параллельное подключение светодиодов — идеальный вариант. Всегда стремитесь к тому, чтобы подключать светодиоды параллельно и ограничивать ток каждого светодиода по отдельности своим резистором.  Если вы используете светодиодные драйверы (стабилизаторы тока), то каждому светодиоду нужно подключать свой драйвер. Именно поэтому параллельные схемы с большим количеством светодиодов становятся слишком дорогими. В реальности приходится идти на компромисс и объединять светодиоды в цепочки.

Последовательное и параллельное соединения диодов.

Если для выпрямительной схемы нельзя выбрать нужный тип диода в соответствии с заданным значением обратного напряжения или прямого тока, то используют два или более однотипных диодов с меньшими значениями параметров, включая эти диоды последовательно или параллельно.

Параллельное соединение диодов

Параллельное соединение диодов

При параллельном соединении диодов из-за возможного разброса параметров их токи будут неодинаковыми. Один из этих токов может превысить максимально допустимое значение, что приведёт к выходу из строя сначала одного, а затем и другого диода. Более равномерное распределения тока между параллельно соединёнными диодами достигается включением последовательно с каждым из них одинаковых по номиналу резисторов R_д. Сопротивление резисторов R_д должно быть в 5…10 раз больше, чем сопротивление диода в прямом направлении. В мощных выпрямительных устройствах для этой же цели используются индуктивные выравниватели токов.

Расчёт параллельного соединения диодов

Для начала расчёта необходимо определить требуемое количество параллельно соединённых диодов, исходя из того, что ток, проходящий через один диод не должен превышать значения максимально допустимого значения тока для данного типа диода, тогда количество параллельно соединённых диодов будет равно

, где

_mTnp

При дробных значениях расчётного количества диодов округление ведётся в большую сторону.

Значение сопротивления добавочных резисторов определяется по формуле

, где

_np.cp

Расчитаное сопротивление добавочных резисторов округляют до ближайшего стандартного сопротивления.

Пример расчёта параллельного соединения диодов

Рассчитать выпрямительную цепь, позволяющую получить выпрямленный ток I_выпр = 550 мА, если используются диоды Д226Б.

Так как средний прямой ток диода Д226Б I_{пр. ср} = 300 мА, то необходимо применить несколько параллельно соединённых диодов с добавочными резисторами. Рассчитаем количество параллельно соединённых диодов, примем k_T = 0,8

Возьмём n = 3.

Найдём значение сопротивлений добавочных резисторов

Выберем резистор из стандартного ряда сопротивлений Е24 (± 5%) R_доб = 6,2 Ом

Последовательное соединение диодов

Последовательное соединение диодов

Для обеспечения возможности работы выбранного типа диода в схеме выпрямителя с обратным напряжением, превышающим его максимально допустимое значение, следует соединять однотипные диоды последовательно. Если параметры не совпадают, то один из диодов оказывается под значительно большим напряжением, чем другой. Это может привести к пробою одного, а затем и другого диода. Выравнивание обратного напряжения на последовательно соединенных диодах достигается шунтированием каждого из диодов резистором R_ш. Ток, протекающий через эти резисторы, должен быть в 5…10 раз больше максимально возможного обратного тока диодов. В мощных высоковольтных выпрямительных устройствах для этой же цели диоды шунтируют конденсаторами С_ш или RC-цепью.

Расчёт последовательного соединения диодов

Для начала расчёта необходимо определить количество последовательно соединенных диодов, исходя из того что падение напряжения на каждом отдельно взятом диоде не должно превышать амплитудного значения напряжения, тогда количество последовательно включённых диодов будет равно

, где

U_m — амплитудное значение напряжения проходящее через диод, k_H – коэффициент нагрузки по напряжению (может принимать значения от 0,5 до 0,8), U_{obp max} — максимально допустимое обратное напряжение диода.

При дробных значениях расчётного количества диодов округление ведётся в большую сторону.

Значение сопротивлений шунтирующих резисторов определяется по формуле

, где

I_{обp max} — максимально допустимый обратный ток диода при максимальной температуре.

Пример расчёта последовательного соединения диодов

Рассчитать выпрямительную цепь для напряжения с амплитудным значением 700В, используя диоды Д226Б.

Так как максимально допустимое обратное напряжение диода U_обр.max = 300В, то для выпрямления необходимо применить цепочку из последовательно соединённых диодов с шунтирующими резисторами. Рассчитаем количество последовательных диодов, примем k_H = 0,7

Возьмём n = 4

Найдём значение сопротивлений шунтирующих резисторов

Выберем резистор из стандартного ряда сопротивлений Е24 (± 5%) R_ш = 1 MОм

Включение дополнительных и шунтирующих резисторов неизбежно связано с увеличением потерь мощности и уменьшением КПД выпрямительной схемы.

Основные выводы

При подключении светодиодной лампы к любому блоку питания учитывается:

• рабочий ток лампочки;
• сопротивление и мощность стабилизирующего элемента;
• для подключения к аккумулятору автомашины при расчетах используется не 12 В, а 14,5 В.

Схема подключения не меняется зависимости от мощности светодиода

При соединении с другими элементами схемы важно учесть полярность, так как ток в этих источниках света течет только в одном направлении

Если используется драйвер, то перед подключением желательно проверить его мощность (особенно, если деталь китайская)

Важно так же учесть, что падение напряжения на лед-лампах зависит от их цвета

Предыдущая
СветодиодыОсобенности устройства и схема светодиодных ламп на 220 В
Следующая
СветодиодыЧто такое светодиод: описание и характеристики

Оцените статью:

Соединение элементов питания и батарей

Источники напряжения обычно называют источниками питания. Для увеличения тока или напряжения, а может и того и другого источники питания (элементы, батареи) могут соединяться вместе. Существует три типа соединения элементов питания:
1. Последовательное соединение элементов.
2. Параллельное соединение элементов.
3. Последовательно-параллельное (смешанное) соединение элементов.

Последовательное соединение элементов.

При последовательном соединении элементов питания выделяются две схемы: последовательно-дополняющая и последовательно-препятствующая.
В последовательно-дополняющей схеме положительный вывод первого элемента питания соединяется с отрицательным выводом второго элемента питания; положительный вывод второго элемента питания соединяется с отрицательным выводом третьего элемента питания и т.д. (рисунок 3.11.)

Рисунок 3.11.Последовательное соединение элементов питания.

При таком соединении источников питания через все элементы будет течь одинаковый ток:

Iобщ=I1=I2=I3

Индексы в обозначениях токов указывают на номера отдельных источников питания (элементов или батарей питания)
А полное напряжение при последовательном соединении равно сумме напряжений (ЭДС) отдельных элементов:

Еобщ = Е1 + Е2 + Е3.

При последовательно-препятствующем включении источников питания, они соединяются друг с другом одноименными выводами. Но на практике такая схема не применяется или применяется, но очень редко.

Параллельное соединение элементов.

При параллельном соединении элементов питания, их одноименные выводы соединяются вместе, то есть плюс к плюсу, минус к минусу (рис 3.12).

Рисунок 3.11.Параллельное соединение элементов питания.

В этом случае общий ток будет равен сумме токов каждого элемента:

Iобщ=I1+I2+I3

Общее напряжение при параллельном включении источников питания будет равно напряжению каждого отдельного источника.

Еобщ = Е1 = Е2 = Е3.

Последовательно-параллельное соединение элементов напряжения.

Источники питания включают по последовательно-параллельной схеме для увеличения, как тока, так и напряжения. При этом основываются на том, что параллельное включение увеличивает силу тока, а последовательное увеличивает общее напряжение. На рисунке 3.13 показаны примеры последовательно-параллельных схем включения элементов питания.

Рисунок 3.11.Последовательно-параллельное соединение элементов питания.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Последовательная зависимость от положения возникает во время восприятия

Эксперимент 1: Последовательная зависимость от воспринимаемого положения

Десять субъектов из 12 показали положительную половину амплитуды DoG, что указывает на то, что воспринимаемое положение в данном испытании было значительно отклонено в направлении положение решетки на предыдущем (т.е. 1-спина) испытании, t (11) = 2,94, p = 0,013 (см. рис. 2a). Даже при сравнении ошибок испытуемых с разницей в позициях двух испытаний назад испытуемые показали достоверно положительные полуамплитуды DoG, t (11) = 3.82, p <0,01 (см. Рис. 2a), что означает, что даже положения решетки представили два испытания с обратным смещением воспринимаемого положения в данном испытании. Для трех и четырех повторных испытаний полуамплитуды DoG незначительно отличались от нуля: 3-back, t (11) = 1,51, p = 0,15; 4-спинка, т (11) = 0,47, п = 0,64 (см. Рис. 2а). Среднее время ответа среди испытуемых составило 1773 ± 612 мс. Таким образом, воспринимаемое положение решетки было сильно увлечено предыдущими положениями решетки, видимыми в течение 5 секунд (одно испытание назад, рис.2а) или 10 секунд назад (два раза назад, рис. 2а).

Мы также проанализировали ширину подгонки DoG, чтобы выяснить, определяет ли временная настройка последовательной зависимости (1-2 попытки назад) ее пространственную настройку (то есть ширину подгонки DoG). Не было статистически значимых различий в ширине между 1, 2, 3 и 4 испытаниями назад, как определено односторонним дисперсионным анализом, F (3, 44) = 0,09, p = 0,96. Кроме того, не было корреляции между половинными амплитудами и полушириной (см.рис.2b; r = -0,16, p = 0,26).

Эксперимент 2: последовательная зависимость положения не является следствием предыдущей двигательной реакции

В эксперименте 1 мы обнаружили, что испытуемые допускали постоянные ошибки, сообщая о предполагаемом местоположении решетки-мишени в текущем испытании, неправильно ориентируя ее в сторону местоположения, представленного на два предыдущих испытания.

В эксперименте 2 мы проверили, может ли это смещение положения быть следствием предыдущей двигательной реакции. В этом эксперименте в 33% испытаний задача регулировки положения была заменена ISI 1250 мс.Важно отметить, что испытания задач по корректировке положения (67% испытаний) и испытания без задач (33% испытаний) были представлены случайным образом, и наблюдатели не знали, попросили ли их ответить на цель или нет. данное испытание. Если последовательная зависимость, наблюдаемая в эксперименте 1, была вызвана предыдущей двигательной реакцией, то мы не должны ожидать никаких доказательств последовательной зависимости в задаче корректировки положения, если ей предшествовало испытание, содержащее ISI вместо задачи корректировки положения.Каждый испытуемый прошел 1380 испытаний, разделенных на 12 блоков.

В обеих последовательностях (см. Рис. 3) испытуемые показали средние положительные полуамплитуды DoG, предыдущий ответ: t (15) = 3,94, p <0,001; отсутствие предыдущего ответа: t (15) = 2,58, p = 0,02, что означает, что последовательная зависимость в воспринимаемой позиции не требовала предшествующей двигательной реакции (см. рис. 3, левая и правая полоски). Мы также обнаружили повышенную серийную зависимость, когда предыдущее испытание требовало ответа (см.рис.3, левая полоса), чем когда она не была (см. Рис. 3, правая полоса), t (15) = 3,87, p <0,001. Это усиление эффекта, наблюдаемого в условиях отклика, вероятно, было связано с тем, что испытуемым была представлена ​​дополнительная точка в том же положении решетки, что усилило эффект последовательной зависимости.

В качестве альтернативного анализа мы могли бы измерить последовательную зависимость от предыдущего ответа, вычислив ось x (см. Рис. 1c) как «скорректированное положение точки в предыдущем испытании (предыдущий ответ, а не предыдущий стимул) минус положение решетки. по текущему делу.Однако в этом конкретном анализе смещения двигательной реакции (Shaffer, 1978; Wing & Kristofferson, 1973), косвенные эффекты (Appelle, 1972; Cicchini, Mikellidou, & Burr, 2017; Mikellidou, Cicchini, Thompson, & Burr, 2015) или другие ошибки локализации (например, Kosovicheva & Whitney, 2017) могут быть последовательными и, следовательно, коррелировать между испытаниями. Любая из этих устойчивых предубеждений может создавать артефакты, напоминающие последовательную зависимость, но на самом деле не связанные между собой. Из-за этих методологических проблем в предыдущих исследованиях измерялась последовательная зависимость между текущими и предыдущими стимулами (Cicchini et al., 2017; Фишер и Уитни, 2014 г .; Liberman et al., 2014; Manassi et al., 2017), а не сравнивать предыдущий и текущий ответ.

Эксперимент 3a и 3b: быстрая последовательная зависимость в восприятии позиции

Недавно было предложено, что последовательная зависимость в восприятии позиции является феноменом мнемонических, а не перцептивных процессов (Bliss, Sun, & D’Esposito, 2017). Используя очень похожую парадигму ^{Footnote 1} , авторы варьировали задержку между предъявлением стимула (очень контрастная черная точка) и ответом (регулировка положения точки) и обнаружили, что положительная последовательная зависимость имеет место для задержек между целевой точкой и регулировочной точкой. это варьировалось от 1 до 10 секунд.Интересно, что при отсутствии задержки между целью и точкой настройки (и без маски) наблюдалось отрицательное последействие вместо положительной серийной зависимости (см. Рис. 2b в Bliss et al., 2017). Известно, что положительная серийная зависимость и отрицательные последствия, вызванные адаптацией, могут быть аддитивными (Alais et al., 2017; Cicchini et al., 2017; Fischer & Whitney, 2014; Taubert, Alais, et al., 2016), а отрицательное последействие Bliss et al. (2017) отчет может быть результатом адаптации к высококонтрастной, заметной целевой точке, как сообщали предыдущие авторы (Hess, Dakin, & Badcock, 1994; Whitaker et al., 1997). Чтобы уменьшить адаптацию и негативные последствия, в эксперименте 1 использовалась маска, следующая за стимулом. В экспериментах 3a и 3b мы удалили маску и изменили контраст цели, чтобы проверить, возникает ли серийная зависимость при нулевой задержке между предъявлением стимула и ответом.

Эксперимент 3a был таким же, как Эксперимент 1, за исключением того, что шумовая маска не была представлена ​​после представления целевой решетки. Шумовая маска была удалена, чтобы сохранить интервал между целевым и ответным стимулом равным нулю.Контраст решетки Майкельсона поддерживался на уровне 30%, как в экспериментах 1 и 2 (высококонтрастный эксперимент). Всего каждый наблюдатель выполнил 450 испытаний.

Субъекты не показали признаков серийной зависимости или отрицательного последействия. Половина амплитуды DoG незначительно отличалась от нуля для любого испытания, 1-back: t (11) = 1,30, p = 0,21; 2-спинка: т (11) = 2,01, p = 0,07; 3-спинка: т (11) = 0,67, р = 0,51; 4-спинка: т (11) = -1.40, p = 0,18 (см. Рис. 4а). Взятые вместе, эти результаты согласуются с предыдущими результатами (Bliss et al., 2017), показывая отсутствие последовательной зависимости для нулевой задержки между стимулом и ответом (эксперимент 3a) и последовательной зависимости для более длительных задержек (эксперименты 1-2). Однако это не означает, что задержка сама по себе является критическим фактором.

Критическим фактором, который модулирует последовательную зависимость воспринимаемого положения, может быть эффективный контраст целевого стимула. Предыдущие данные показали, что воспринимаемый контраст решетки может быть ослаблен последующей (обратной) маской (Breitmeyer, Rudd, & Dunn, 1981; Breitmeyer, Hoar, Randall, & Conte, 1984; Breitmeyer & Ogmen, 2000; Kolers, 1962). ; Raab, 1963), и, как следствие, ослабляется его отрицательное последействие (Gibson & Radner, 1937; Keck, Palella, & Pantle, 1976; Stecher, Sigel, & Lange, 1973).Соответственно, решетка с обратной маской показала последовательную зависимость (эксперименты 1 и 2), тогда как решетка без маски не показала никаких доказательств последовательной зависимости (эксперимент 3a). Следовательно, если очевидное уменьшение контрастности цели (а не задержка) определяет силу последовательной зависимости, мы предположили, что последовательная зависимость должна возникать с решеткой с более низким контрастом. В эксперименте 3b мы проверили эту гипотезу.

В эксперименте 3b мы уменьшили контраст решетки Майкельсона до 4% (эксперимент с низким контрастом).Наша цель была двоякой. Во-первых, за счет уменьшения контраста любое негативное последействие, вызванное адаптацией (Hess et al., 1994; McGraw et al., 2002; Whitaker et al., 1997), будет уменьшено. Во-вторых, испытуемые вынуждены уделять больше внимания решетке-мишени. Поскольку серийная зависимость сильно зависит от внимания (Fischer & Whitney, 2014), ожидается более сильное положительное смещение.

В соответствии с нашей гипотезой, испытуемые демонстрировали последовательную зависимость, даже при нулевой задержке между мишенью и ответным стимулом.Это справедливо для одного и двух испытаний назад, 1-back: т (10) = 5,18, p <0,001; 2-спинка: т (10) = 9,36, п <0,001; 3-спинка: т (10) = 2,07, п = 0,06; 4-спинка: т (10) = 1,15, п = 0,27 (см. Рис. 4б). Следовательно, критическим фактором, определяющим силу последовательной зависимости в суждениях о локализации, является яркостный контраст (или неопределенность в более общем смысле), а не задержка. Последовательная зависимость от позиции — это быстрый механизм, искажающий восприятие позиции сразу после предъявления стимула.Хотя последовательная зависимость все еще может модулироваться краткосрочной рабочей памятью (Bliss et al., 2017; Fritsche, Mostert, & de Lange, 2017), ее нельзя рассматривать как чисто зависимый от задержки или основанный на рабочей памяти процесс, отделенный от его перцептивный компонент (см. также Cicchini et al., 2017).

Построение последовательной зависимости в рабочей памяти цвета

1.

de Lange, F. P., Heilbron, M. & Kok, P. Как ожидания формируют восприятие ?. Trends Cogn. Sci. (Regul.Ред.) 22 , 764–779 (2018).

Google Scholar

2.

Киёнага А., Шимека Дж. М., Блисс Д. П. и Уитни Д. Серийная зависимость восприятия, внимания и памяти. Trends Cogn. Sci. (Рег. Ред.) 21 , 493–497 (2017).

Google Scholar

3.

Блисс, Д. П., Сан, Дж. Дж. И Д’Эспозито, М. Серийная зависимость отсутствует во время восприятия, но увеличивает визуальную рабочую память. Sci. Отчет 7 , 14739 (2017).

ADS PubMed PubMed Central Google Scholar

4.

Ся Ю., Либерман А., Яманаши Лейб А. и Уитни Д. Серийная зависимость в восприятии привлекательности. J. Vis. 15 , 1219 (2015).

Google Scholar

5.

Манасси, М., Либерман, А., Косовичева, А., Чжан, К.И Уитни, Д. Серийная зависимость позиции возникает во время восприятия. Психон. Бык. Ред. 25 , 2245–2253 (2018).

PubMed Google Scholar

6.

Czoschke, S., Fischer, C., Beitner, J., Kaiser, J. & Bledowski, C. Два типа последовательной зависимости в зрительной рабочей памяти. руб. J. Psychol. 110 , 256–267 (2018).

PubMed Google Scholar

7.

Alais, D., Kong, G., Palmer, C. и Clifford, C. Направление взгляда показывает положительную последовательную зависимость. J. Vis. 18 , 11 (2018).

PubMed Google Scholar

8.

Манасси, М., Либерман, А., Чейни, В. и Уитни, Д. Воспринимаемая стабильность сцен: последовательная зависимость в ансамблевых представлениях. Sci. Отчет 7 , 1971 (2017).

ADS PubMed PubMed Central Google Scholar

9.

Самаха, Дж., Свитцки, М. и Постл, Б. Р. Уверенность повышает последовательную зависимость в оценке ориентации. BioRxiv https://doi.org/10.1101/369140 (2018).

Артикул Google Scholar

10.

Суарес-Пинилья, М., Сет, А. К. и Розебум, В. Серийная зависимость в восприятии визуальной дисперсии. J. Vis. 18 , 4 (2018).

PubMed PubMed Central Google Scholar

11.

Фишер, Дж. И Уитни, Д. Серийная зависимость в визуальном восприятии. Нац. Neurosci. 17 , 738–743 (2014).

CAS PubMed PubMed Central Google Scholar

12.

Либерман, А., Чжан, К. и Уитни, Д. Последовательная зависимость способствует стабильности объекта во время окклюзии. J. Vis. 16 , 16 (2016).

PubMed PubMed Central Google Scholar

13.

Alexi, J. et al. Прошлый визуальный опыт влияет на оценку размеров тела. Sci. Отчет 8 , 215 (2018).

ADS PubMed PubMed Central Google Scholar

14.

Cicchini, G. M., Anobile, G. & Burr, D. C. Компрессионное отображение числа в пространство отражает механизмы динамического кодирования, а не статическое логарифмическое преобразование. Proc. Natl. Акад. Sci. США 111 , 7867–7872 (2014).

ADS CAS PubMed PubMed Central Google Scholar

15.

Фриче М., Мостерт П. и де Ланге Ф. П. Противоположные эффекты недавней истории на восприятие и решение. Curr. Биол. 27 , 590–595 (2017).

CAS PubMed Google Scholar

16.

Тауберт, Дж., Элайс, Д. и Берр, Д. Различные стратегии кодирования для восприятия стабильных и изменчивых черт лица. Sci. Отчет 6 , 32239 (2016).

ADS CAS PubMed PubMed Central Google Scholar

17.

Тауберт, Дж., Ван дер Бург, Э. и Элайс, Д. Любовь со второго взгляда: последовательная зависимость привлекательности лица в парадигме онлайн-свиданий. Sci. Отчет 6 , 22740 (2016).

ADS CAS PubMed PubMed Central Google Scholar

18.

Lieder, I. et al. Смещение восприятия указывает на медленное обновление при аутизме и быстрое забывание при дислексии. Нац. Neurosci. 22 , 256–264 (2019).

CAS PubMed Google Scholar

19.

Хуанг, Дж. Искажения при припоминании из зрительной памяти: два класса аттракторов в действии. J. Vis. 10 , 1–27 (2010).

CAS PubMed Google Scholar

20.

Чиккини, Г. М., Микеллиду, К. и Берр, Д. Серийные зависимости действуют непосредственно на восприятие. J. Vis. 17 , 6 (2017).

PubMed Google Scholar

21.

Пападимитриу, К., Уайт, Р. Л. и Снайдер, Л. Х. Призраки в машине II: нейронные корреляты помех памяти из предыдущего испытания. Cereb. Cortex 27 , 2513–2527 (2017).

PubMed Google Scholar

22.

Пападимитриу, К., Фердоаш, А. и Снайдер, Л. Х. Призраки в машине: вмешательство памяти из предыдущего испытания. J. Neurophysiol. 113 , 567–577 (2015).

PubMed Google Scholar

23.

Либерман А., Фишер Дж. И Уитни Д. Серийная зависимость в восприятии лиц. Curr. Биол. 24 , 2569–2574 (2014).

CAS PubMed PubMed Central Google Scholar

24.

Cicchini, G. M., Mikellidou, K. & Burr, D. C. Функциональная роль серийной зависимости. Proc. Биол. Sci. 285 , 20181722 (2018).

PubMed PubMed Central Google Scholar

25.

Ashourian, P. & Loewenstein, Y. Байесовский вывод лежит в основе систематической ошибки сокращения в задачах отложенного сравнения. PLoS ONE 6 , e19551 (2011).

ADS CAS PubMed PubMed Central Google Scholar

26.

Витцель, К., Олкконен, М., Гегенфуртнер, К. Р. Байесовская модель цветового эффекта памяти. Iperception 9 , 2041669518771715 (2018).

PubMed PubMed Central Google Scholar

27.

Narain, D., Remington, E. D., Zeeuw, C. I. D. и Jazayeri, M. Мозжечковый механизм для изучения априорных распределений временных интервалов. Нац. Commun. 9 , 469 (2018).

ADS PubMed PubMed Central Google Scholar

28.

Олкконен, М., Маккарти, П. Ф. и Оллред, С. Р. Смещение центральной тенденции в восприятии цвета: эффекты внутреннего и внешнего шума. J. Vis. 14 , 5 (2014).

PubMed Google Scholar

29.

Akrami, A., Kopec, C.D., Diamond, M.E. & Brody, C.D. Задняя теменная кора представляет собой сенсорный анамнез и опосредует его влияние на поведение. Природа 554 , 368–372 (2018).

ADS CAS PubMed Google Scholar

30.

Чекки, Г. А., Рао, А. Р., Сяо, Ю. и Каплан, Е. Статистика естественных сцен и обработка цвета коры головного мозга. J. Vis. 10 , 21 (2010).

PubMed PubMed Central Google Scholar

31.

Hardman, K. O., Vergauwe, E. & Ricker, T. J. Категориальные представления рабочей памяти используются для отложенной оценки непрерывных цветов. J. Exp. Psychol. Гул. Восприятие. Выполнять. 43 , 30–54 (2017).

PubMed Google Scholar

32.

Бэ, Г.-Й., Олкконен, М., Оллред, С. Р., Уилсон, К. и Фломбаум, Дж. И. Стимул-специфическая изменчивость цветовой рабочей памяти с отложенной оценкой. J. Vis. 14 , 7 (2014).

PubMed Google Scholar

33.

Паничелло, М. Ф., Де Паскуале, Б., Подушка, Дж. У. и Бушман, Т. Дж. Динамика исправления ошибок в зрительной рабочей памяти. Нац. Commun. 10 , 3366 (2019).

ADS PubMed PubMed Central Google Scholar

34.

Gold, J. I., Law, C.-T., Connolly, P. & Bennur, S. Относительное влияние априорных и сенсорных данных на переменную глазодвигательного решения во время перцептивного обучения. Дж.Neurophysiol. 100 , 2653–2668 (2008).

PubMed PubMed Central Google Scholar

35.

Сотиропулос, Г., Зейтц, А. Р. и Сериес, П. Изменение ожиданий относительно скорости изменяет воспринимаемое направление движения. Curr. Биол. 21 , R883 – R884 (2011).

CAS PubMed Google Scholar

36.

Соуза, А.С., Рерко, Л., Линь, Х.-Й. И Оберауэр, К. Сосредоточенное внимание улучшает рабочую память: последствия для моделей с гибкими ресурсами и дискретной емкостью. Аттен. Восприятие. Психофизика. 76 , 2080–2102 (2014).

PubMed Google Scholar

37.

Чжан, В. и Лак, С. Дж. Дискретные представления с фиксированным разрешением в визуальной рабочей памяти. Природа 453 , 233–235 (2008).

ADS CAS PubMed PubMed Central Google Scholar

38.

Фостер, Дж. Дж., Бсалес, Э. М., Джаффе, Р. Дж. И Эйв, Э. Активность альфа-диапазона выявляет спонтанные представления пространственного положения в зрительной рабочей памяти. Curr. Биол. 27 , 3216–3223 (2017).

CAS PubMed PubMed Central Google Scholar

39.

Wimmer, K., Nykamp, ​​D. Q., Constantinidis, C. & Compte, A. Динамика выпуклого аттрактора в префронтальной коре объясняет точность поведения в пространственной рабочей памяти. Нац. Neurosci. 17 , 431–439 (2014).

CAS PubMed Google Scholar

40.

Shafto, M.A. et al. Протокол исследования Кембриджского центра старения и нейробиологии (Cam-CAN): перекрестное, многопрофильное, многопрофильное исследование здорового когнитивного старения. BMC Neurol. 14 , 204 (2014).

PubMed PubMed Central Google Scholar

41.

Тейлор, Дж. Р. et al. Хранилище данных Кембриджского центра старения и нейробиологии (Cam-CAN): структурные и функциональные данные МРТ, МЭГ и когнитивные данные из поперечной выборки продолжительности жизни взрослых. Neuroimage 144 , 262–269 (2017).

PubMed PubMed Central Google Scholar

42.

Бэйс, П. М., Каталао, Р. Ф. Г. и Хусейн, М. Точность визуальной рабочей памяти устанавливается путем выделения общего ресурса. J. Vis. 9 , 1–11 (2009).

PubMed Google Scholar

43.

Алмейда, Р., Барбоса, Дж. И Компте, А. Основа нейронной схемы для визуально-пространственной точности рабочей памяти: вычислительное и поведенческое исследование. J. Neurophysiol. 114 , 1806–1818 (2015).

PubMed PubMed Central Google Scholar

44.

Нассар, М.Р., Хелмерс, Дж. К. и Франк, М. Дж. Чанкинг как рациональная стратегия сжатия данных с потерями в визуальной рабочей памяти. Psychol. Ред. 125 , 486–511 (2018).

PubMed PubMed Central Google Scholar

45.

Чжан, В. и Лак, С. Дж. Внезапная смерть и постепенное ухудшение зрительной рабочей памяти. Psychol. Sci. 20 , 423–428 (2009).

PubMed PubMed Central Google Scholar

46.

Нильссон, Т. Х. и Нельсон, Т. М. Отсроченные совпадения монохроматических оттенков указывают на характеристики зрительной памяти. J. Exp. Psychol. Гул. Восприятие. Выполнять. 7 , 141–150 (1981).

CAS PubMed Google Scholar

47.

Ванделл Б. А., Дюмулен С. О. и Брюэр А. А. Карты полей зрения в коре головного мозга человека. Нейрон 56 , 366–383 (2007).

CAS PubMed Google Scholar

48.

Джонсон, Э. Н. и Маллен, К. Т. Цвет коры головного мозга. В Human Color Vision (ред. Кремерс, Дж. и др. ) 189–217 (Springer, Нью-Йорк, 2016).

Google Scholar

49.

Бохон, К. С., Герман, К. Л., Хансен, Т. и Конвей, Б. Р. Представление перцептивного цветового пространства в задней нижней височной коре макака (комплекс V4). Eneuro https://doi.org/10.1523/ENEURO.0039-16.2016 (2016).

Артикул PubMed PubMed Central Google Scholar

50.

Чанг, Л., Бао, П. и Цао, Д. Ю. Изображение цветных объектов в цветовых пятнах макака. Нац. Commun. 8 , 2064 (2017).

ADS PubMed PubMed Central Google Scholar

51.

Паничелло, М. Ф. и Бушман, Т. Дж. Селективный контроль рабочей памяти в префронтальной, теменной и зрительной коре. BioRxiv https://doi.org/10.1101/2020.04.07.030718 (2020).

Артикул Google Scholar

52.

Compte, A., Brunel, N., Goldman-Rakic, P. S. & Wang, X. J. Синаптические механизмы и сетевая динамика, лежащие в основе пространственной рабочей памяти в модели кортикальной сети. Cereb. Cortex 10 , 910–923 (2000).

CAS PubMed Google Scholar

53.

Килпатрик, З. П. Синаптические механизмы вмешательства в рабочую память. Sci. Отчет 8 , 7879 (2018).

ADS PubMed PubMed Central Google Scholar

54.

Carter, E. & Wang, X.-J. Растормаживание, опосредованное каннабиноидами, и рабочая память: динамическое взаимодействие множественных механизмов обратной связи в модели непрерывного аттрактора префронтальной коры. Cereb. Cortex 17 (Дополнение 1), i16-26 (2007).

PubMed Google Scholar

55.

Блисс, Д. П. и Д’Эспозито, М. Синаптическое увеличение в модели кортикального контура воспроизводит последовательную зависимость в зрительной рабочей памяти. PLoS ONE 12 , e0188927 (2017).

PubMed PubMed Central Google Scholar

56.

Stein, H. et al. Нарушенная серийная зависимость предполагает дефицит синаптического потенцирования при энцефалите против NMDAR и шизофрении. BioRxiv https://doi.org/10.1101/830471 (2019).

Артикул Google Scholar

57.

Barbosa, J. et al. Взаимодействие между постоянной активностью и динамикой без активности в префронтальной коре во время рабочей памяти. Нац. Neurosci. https://doi.org/10.1038/s41593-020-0644-4 (2020).

Артикул PubMed Google Scholar

58.

Кастильо, П. Э., Юнтс, Т. Дж., Чавес, А. Э. и Хашимотодани, Ю. Эндоканнабиноидная передача сигналов и синаптическая функция. Нейрон 76 , 70–81 (2012).

CAS PubMed PubMed Central Google Scholar

59.

Паничелло, М. Ф., Де Паскуале, Б., Подушка, Дж. У. и Бушман, Т. Динамика исправления ошибок в зрительной рабочей памяти. BioRxiv https://doi.org/10.1101/319103 (2018).

Артикул Google Scholar

60.

Oberauer, K. & Lin, H.-Y. Интерференционная модель зрительной рабочей памяти. Psychol. Ред. 124 , 21–59 (2017).

PubMed Google Scholar

61.

van den Berg, R., Shin, H., Chou, W.-C., George, R. & Ma, W.J. Изменчивость в точности кодирования определяет ограничения кратковременной зрительной памяти. Proc. Natl. Акад. Sci. США 109 , 8780–8785 (2012).

ADS PubMed PubMed Central Google Scholar

Контекстная информация поддерживает последовательную зависимость нескольких визуальных объектов по эпизодам памяти

Поведенческая парадигма

В четырех экспериментах испытуемые запоминали два визуальных объекта за испытание.После небольшой задержки один из них был подан для отчета (рис. 1). В то время как направление движения служило функцией запоминаемого содержимого, объекты дополнительно отличались несколькими особенностями контекста. Эти контекстные функции были релевантными для задачи, когда они служили сигналом для обозначения целевого объекта, в противном случае они не имели отношения к задаче. Мы оценили серийную зависимость, то есть систематическое смещение ошибки отчета к объектам предыдущего испытания, между объектом, которому была дана ссылка, и каждым объектом из предыдущего испытания с учетом их контекста конгруэнтности.В эксперименте 1 два объекта были представлены последовательно с цветом и порядковой позицией как релевантная для задачи и нерелевантная контекстная характеристика, соответственно. В эксперименте 2 мы изменили актуальность задач этих контекстных функций. В экспериментах 3 и 4 мы использовали цвет и пространственное положение в качестве релевантных для задачи контекстных характеристик, соответственно, и объекты были представлены одновременно. В четырех экспериментах мы изучали влияние трех различных контекстных характеристик: цвета, порядкового и пространственного положения.Эти контекстные особенности могут по-разному влиять на серийную зависимость, поскольку они качественно различаются. Во-первых, в то время как цвет и пространственное положение присущи визуальному представлению объекта, последовательное положение возникает исключительно во временном контексте эпизода воспоминания с последовательно представленными объектами. Во-вторых, в отличие от цвета, временная и пространственная информация считается фундаментальной для определения идентичности объекта ¹⁹ .

Рис. 1: Экспериментальная парадигма и определение объекта.

a В каждом испытании участники должны были запоминать направления движения (обозначенные здесь серыми стрелками только для иллюстрации) двух последовательно представленных точечных полей (S1 и S2) и сообщать об одном из них после небольшой задержки, регулируя ориентацию линия (возможные направления регулировки указаны здесь серыми стрелками только для иллюстрации). Целевой объект, о котором должно было быть сообщено, был обозначен цветом (Эксперимент 1) или последовательным положением (Эксперимент 2). b Каждый объект может быть определен относительно его характеристики содержимого, здесь направление движения 25 °, и относительно его контекстных характеристик, здесь цвета (красный) и порядкового положения (первое в последовательности, S1).Контекстная функция, с помощью которой цели были поданы, была релевантной для задачи функцией, тогда как другая функция не имела отношения к задаче (например, цвет и порядковая позиция в Эксперименте 1, соответственно). c Мы оценили влияние трех факторов на ошибку ответа для элемента (цели) в текущем испытании: цвет (такой же или разный), порядковое положение (такое же или разное) и роль (цель или нецелевое) предмет в предыдущем испытании.

Эксперимент 1

В соответствии с предыдущими выводами ^3,6,15,20 , мы наблюдали значительную последовательную зависимость между испытаниями, даже несмотря на то, что два элемента были закодированы для каждого испытания, а один был подан для отчета.В частности, заявленное направление движения в текущем испытании систематически привлекало элементы, представленные в предыдущем испытании. Это притяжение следовало кривой в форме производной Гаусса (DoG) с параметром амплитуды 1,59 ° (исходное SD: 0,303 °, нижние 95% перестановок между -1,38 ° и 0,89 °, p <0,001, d _est = 0,966, R ² = 0,078) и параметр w , равный 0,033, что соответствует ширине 34.38 ° (полная ширина на половине высоты, FWHM). Мы провели односторонние тесты на перестановку ( n = 20), чтобы оценить, отличается ли это притяжение от нуля и между условиями.

Важно отметить, что конгруэнтность контекстных признаков повлияла на серийную зависимость содержания объекта (рис. 2). Последовательная зависимость модулировалась релевантным для задачи контекстным признаком, т. Е. Цветом, поскольку она была сильнее, когда текущий элемент имел тот же цвет, что и стимул в предыдущем испытании (амплитуда = 2,32 °, SD = 0,295 °, ниже 95% перестановки между -1.95 ° и 1,16 °, p <0,001, d _est = 1,359 , R ² = 0,091) по сравнению с тем, когда их цвета различались (амплитуда = 0,87 °, SD = 0,646 °, ниже 95% перестановок между -1,30 ° и 0,84 °, p = 0,038 , d _est = 0,252, R ² = 0,012) (разница амплитуд = 1,46 °, p <0,001 , d _est = 0.856,). Точно так же наблюдаемая серийная зависимость была настроена более широко, когда текущий элемент имел тот же цвет, что и предыдущий стимул (FWHM = 37,45 °), по сравнению с тем, когда они имели разные цвета (FWHM = 28,59 °) ( w разница: -0,010 , равна разнице FWHM: 8,86 °, p = 0,047 , d _est = 0,727). Напротив, не относящаяся к задаче серийная позиция модулировала серийную зависимость только частично. Сила последовательной зависимости, когда текущий стимул предъявлялся в одной и той же последовательной позиции (амплитуда = 1.56 °, SD = 0,331 °, нижние 95% перестановок между -1,60 ° и 0,89 °, p <0,001, d _est = 0,520 , R ² = 0,052) было сравнимо с тем, когда они были представлены в разных последовательных положениях (амплитуда = 1,76 °, SD = 0,303 °, ниже 95% перестановок между -1,43 ° и 0,94 °, p <0,001, d _est = 1,178 , R ² = 0,046) (разность амплитуд = -0.20 °, p = 0,239 , d _est = −0,328). Однако мы наблюдали более широко настроенную серийную зависимость, когда текущие и предыдущие стимулы предъявлялись в одной и той же последовательной позиции (FWHM = 39,45 °) по сравнению с тем, когда их последовательные положения различались (FWHM = 28,03 °) ( w разница: -0,012 , равна разнице FWHM: 11,42 °, p = 0,011 , d _est = 0,266).

Рис. 2: Результаты эксперимента 1.

Ошибки ответа (ордината) показаны как функция разности направлений движения (абсцисса) между элементом предыдущего испытания и целью текущего испытания. Положительные значения на оси абсцисс указывают на то, что целевое направление было смещено против часовой стрелки относительно элемента предыдущего испытания. Положительные значения на ординате указывают на отклонение направления отклика по часовой стрелке от истинного целевого направления. Серийная зависимость была выявлена ​​с помощью средних групповых ошибок ответа (тонкие линии), с соответствующими заштрихованными областями, отображающими стандартную ошибку среднего группового значения.Производная по Гауссу (DoG, соответствие модели показано жирными линиями) была подогнана к ошибкам ответа для оценки систематической ошибки ответа. Сплошные линии указывают на значительную погрешность, а пунктирные линии — на незначительную погрешность. Черные закрашенные кружки и черные пунктирные линии показывают амплитуды и FWHM соответствия DoG и сопровождаются символом, указывающим результат прямого сравнения оценок параметров. (односторонние перестановочные тесты, 20 участников). Звездочки указывают на значение p <0.05, а метка «н.с.» указывает на незначительный результат со значением p ≥ 0,05. a И амплитуда, и ширина последовательной зависимости были больше между предметами одного цвета, чем между предметами разного цвета (разница амплитуд: p < 0,001 , разница в ширине: p = 0,047 ). b Ширина серийной зависимости была больше между изделиями с одинаковыми порядковыми позициями, чем между изделиями с разными порядковыми позициями (разница амплитуд : p = 0.239 , разница ширины: p = 0,011 ). c Значительная последовательная зависимость наблюдалась от цели предыдущего испытания, но не от предыдущего нецелевого (разница амплитуд: p < 0,001 , разница ширины: p < 0,001 ). Исходные данные представлены в виде файла исходных данных.

Эксперимент 1 выявил значительную привлекательную предвзятость только к целевым элементам предыдущего испытания.Мы наблюдали последовательную зависимость от предыдущих целей (амплитуда = 2,99 °, SD = 0,428 °, более низкие 95% перестановок между -2,80 ° и 1,40 °, p <0,001, d _est = 1,351, R ² = 0,140; FWHM = 38,30 °), но не в направлении предыдущих нецелевых (амплитуда = 0,71 °, SD = 0,699 °, ниже 95% перестановок между -1,23 ° и 0,72 °, p = 0,0519, d _est = 0,358 , ² = 0.003 ; FWHM = 11,33 °). Следовательно, параметры анализа аппроксимации кривой не могли быть интерпретированы для эффекта от нецелевых. Однако, поскольку тест перестановки был почти значимым, мы рассчитали тест между двумя факторами, который показал более сильную и более широко настроенную последовательную зависимость от целей, чем от нецелевых (разница амплитуд = 2,28 °, p <0,001 , d _est = 1.042; w разница: −0.070, равняется разнице FWHM: 26,97 °, p <0,001 , d _est = 1,359), но подчеркните, что этот результат следует интерпретировать осторожно.

В дополнение к вычисленным контрастам мы исследовали возможные взаимодействия между цветом, порядковой позицией и предыдущей ролью, но не нашли значительных результатов (подробности на дополнительном рисунке 1 и дополнительной таблице 1). Кроме того, мы вычислили 4-сторонний дисперсионный анализ с цветовыми факторами, предыдущим положением элемента, текущим положением элемента и предыдущей ролью (см. Дополнительный рис.2 и Дополнительная таблица 5).

Эксперимент 2

Совпадение цвета и порядкового номера по-разному повлияло на серийную зависимость в Эксперименте 1. Это наблюдение нельзя было однозначно отнести к релевантности задачи, потому что обе особенности также различались по значимости. В то время как цвет является важной характеристикой, присущей внешнему виду предмета, последовательное положение определяет временную структуру испытания и является неотъемлемой частью кодирования стимулов. Чтобы проверить, определяет ли релевантность задачи контекстной функции модуляцию конгруэнтностью контекста, мы поменяли местами релевантность задачи обеих функций в эксперименте 2.Мы также устранили любую связь между порядковым номером и цветом, позволив двум предметам в испытании иметь один и тот же цвет. Более того, эксперимент 1 только выявил значительную привлекательную склонность к предыдущим целевым элементам. Чтобы получить более убедительные доказательства потенциальной серийной зависимости от нецелевых, мы значительно увеличили количество участников.

Мы снова наблюдали последовательную зависимость между испытаниями, когда целевой элемент был подан через последовательное положение с амплитудой 2.00 ° (SD = 0,200 °, ниже 95% перестановок между -0,93 ° и 0,57 °, p <0,001 , d _est = 1,123, R ² = 0,118) и FWHM 34,63 °. Мы провели односторонние тесты на перестановку ( n = 49), чтобы оценить, отличается ли это притяжение от нуля и между условиями.

Важно отметить, что эксперимент 2 разрешил два открытых вопроса. Во-первых, он показал, что актуальность задачи определяет влияние контекстной конгруэнтности на серийную зависимость.Мы обнаружили, что последовательная зависимость модулируется контекстным признаком задачи, то есть последовательной позицией (рис. 3). Сила последовательной зависимости была увеличена, когда текущий стимул был представлен в той же последовательной позиции, что и предыдущий (амплитуда = 2,33 °, SD = 0,204 °, более низкие 95% перестановок между -1,15 ° и 0,71 °, p < 0,001 , d _est = 1,243, R ² = 0,106) по сравнению с тем, когда они были представлены в разных последовательных позициях (амплитуда = 1.82 °, SD = 0,200 °, ниже 95% перестановок между -0,87 ° и 0,56 °, p <0,001 , d _est = 0,881, R ² = 0,045) ( разность амплитуд = 0,52 °, p = 0,009 , d _est = 0,387). Кроме того, мы наблюдали более широко настроенную серийную зависимость между элементами в одном и том же (FWHM = 44,60 °) по сравнению с различными серийными позициями (FWHM = 26,04 °) ( w разница: -0.018, равно разнице FWHM: 18,56 °, p <0,001 , d _est = 0,840). Напротив, цвет, который был актуален для задачи в эксперименте 1, но не имел отношения к задаче в эксперименте 2, не модулировал последовательную зависимость. Серийная зависимость, когда текущий элемент имел тот же цвет, что и предыдущий стимул (амплитуда = 2,06 °, SD = 0,195 °, ниже 95% перестановок между -1,19 ° и 0,65 °, p <0,001 , d _est = 0.674, R ² = 0,076) было сравнимо с тем, когда их цвета различались (амплитуда = 1,93 °, SD = 0,275 °, ниже 95% перестановок между -1,33 ° и 0,63 °, p <0,001 , d _est = 0,812, R ² = 0,057) (разность амплитуд = 0,13 °, p = 0,347 , d _est = — 0,065). То же самое верно и для ширины настройки (тот же цвет: FWHM = 36.00 °, разные цвета: FWHM = 33,27 °, w разница = -0,0003, равна FWHM разница: 2,73 °, p = 0,228 , d _est <0,001).

Рис. 3: Результаты эксперимента 2.

Последовательная зависимость (ордината) показана как функция разности направлений движения (абсцисса) между элементом предыдущего испытания и целью текущего испытания. Подробнее см. Рис. 2 и Методы. Серийная зависимость была выявлена ​​с помощью средних групповых ошибок ответа (тонкие линии), с соответствующими заштрихованными областями, отображающими стандартную ошибку среднего группового значения.Модель DoG (показана жирными линиями) была адаптирована к ошибкам ответа для оценки систематической ошибки ответа. Сплошные линии указывают на значительную систематическую ошибку, а пунктирные линии — на незначительную. Черные закрашенные кружки и черные пунктирные линии показывают амплитуды и FWHM подгонок DoG и сопровождаются символом, указывающим результат прямого сравнения оценок параметров (односторонние тесты перестановки, 49 участников). Звездочки указывают на значение p <0.05 и «н.с.» указывает на несущественный результат со значением p ≥ 0,05. a Серийная зависимость существенно не различалась между предметами одного цвета и разных цветов (разница амплитуд: p = 0,347, разница ширины: p = 0,228). b И амплитуда, и ширина серийной зависимости были больше между изделиями с одинаковыми порядковыми позициями, чем между изделиями с разными порядковыми позициями (разница амплитуд: p = 0.009, разница ширины: p <0,001). c И амплитуда, и ширина последовательной зависимости были больше для предыдущих целей, чем для нецелевых (разница амплитуд: p <0,001, разница в ширине: p <0,001) Исходные данные представлены в виде файла исходных данных.

Во-вторых, эксперимент 2 разрешил открытый вопрос, могут ли нецелевые объекты из предыдущих испытаний также вызывать серийную зависимость. Увеличивая количество испытуемых, мы действительно наблюдали привлекательную тенденцию к предыдущим нецелевым показателям, хотя и с заметно меньшей амплитудой для предыдущих нецелевых целей, чем для целей (предыдущие цели: амплитуда = 3.46 °, SD = 0,240 °, ниже 95% перестановок между -1,59 ° и 0,92 °, p <0,001 , d _est = 1,654, R ² = 0,176; предыдущие нецелевые: амплитуда = 0,60 °, SD = 0,297 °, нижние 95% перестановок между -0,62 ° и 0,44 °, p = 0,009 , d _est = 0,421, R ² = 0,005; разница амплитуд между предыдущими целями и нецелевыми: 2.86 °, p <0,001 , d _est = 1,192). Это также верно для ширины настройки (предыдущие цели: FWHM = 37,98; предыдущие нецелевые: FWHM = 22,28 °; w разница = -0,021, равна разнице FWHM: 15,70 °, p <0,001 , d _est = 1,070).

Мы снова исследовали возможные взаимодействия, которые не дали существенных результатов (см. Дополнительный рис. 1 и дополнительную таблицу 2), и вычислили 4-х сторонний дисперсионный анализ (см. Дополнительный рис.2 и дополнительная таблица 6).

Эксперименты 3 и 4

Чтобы обобщить результаты экспериментов 1 и 2 на частую ситуацию одновременного предъявления объектов, мы представили два цветных точечных поля одновременно в разных пространственных положениях (рис. 4) в экспериментах 3 и 4. В эксперименте 3, пространственное положение не имело отношения к задаче, а цвет использовался в качестве ориентира (аналогично эксперименту 1), тогда как в эксперименте 4 пространственное положение было релевантным для задачи контекстным признаком.

Рис. 4: Экспериментальная парадигма экспериментов 3 и 4.

В каждом испытании участники должны были запоминать направления движения (обозначенные здесь серыми стрелками только для иллюстрации) двух одновременно представленных точечных полей (S1 и S2) и сообщать об одном из них после небольшой задержки путем настройки ориентации линии (возможные направления настройки указаны здесь серыми стрелками только для иллюстрации). Целевой объект, о котором должно было быть сообщено, был обозначен цветом (эксперимент 3) или пространственным положением (эксперимент 4).

Эксперименты 3 и 4 показали значительную последовательную зависимость между испытаниями (Эксперимент 3: амплитуда = 2,14 °, SD = 0,383 °, более низкие 95% перестановок между -1,98 ° и 1,18 °, p <0,001 , d _est = 0,551, R ² = 0,042 и FWHM = 40,33 °; эксперимент 4: амплитуда = 1,51 °, SD = 0,477 °, нижние 95% перестановок между -1,72 ° и 0,90 °, p <0,001 , d _est = 0.807, R ² = 0,034 и FWHM = 32,65 °). Мы провели односторонние тесты на перестановку ( n = 20 в каждом эксперименте), чтобы оценить, отличалось ли это притяжение от нуля и между условиями.

Важно отметить, что эксперименты 3 и 4 показали, что результаты экспериментов 1 и 2, касающиеся влияния релевантных для задачи контекстных характеристик, обобщаются на условия с одновременным представлением (рис. 5). В частности, в эксперименте 3 мы наблюдали, что релевантный для задачи цвет влияет на серийную зависимость, что демонстрируется значительным смещением привлекательности, когда текущий стимул имел тот же цвет, что и предыдущий (амплитуда = 2.13 °, SD = 0,492 °, ниже 95% перестановок между -2,31 ° и 1,37 °, p <0,001 , d _est = 0,585, R ² = 0,052; FWHM = 45,66 °), но не между стимулами разного цвета (амплитуда = -0,62 °, SD = 0,991 °, нижние 95% перестановок между -1,77 ° и 1,08 °, p = 0,224, d _est = −0,806 , R ² = 0,011 ; FWHM = 113.32 °). Прямое статистическое сравнение, к которому следует относиться с осторожностью, показало значительную разницу амплитуд в 2,74 ° ( p = 0,005 , d _est = 1,112), но не было существенной разницы между шириной настройки ( w разница: 0,015, равна разнице FWHM: -67,65 °, p = 0,153 , d _est = 0,604). Точно так же эксперимент 4 также показал, что относящаяся к задаче пространственная позиция модулирует последовательную зависимость.Мы наблюдали привлекательное смещение, когда текущий стимул был представлен в том же пространственном положении, что и предыдущий (амплитуда = 3,01 °, SD = 0,409 °, более низкие 95% перестановок между -2,75 ° и 1,58 °, p <0,001 , d _est = 0,879, R ² = 0,040 ; FWHM = 39,41 °), но не между стимулами с разными пространственными положениями (амплитуда = 1,26 °, SD = 0,891 °, ниже 95 % перестановок между -2,68 ° и 1.63 °, p = 0,137 , d _est = 0,358, R ² = 0,010; FWHM = 42,22 °). Контраст, к которому снова следует относиться с осторожностью, указывает на более сильную последовательную зависимость между предметами с одинаковым пространственным положением по сравнению с предметами с другим пространственным положением (разность амплитуд = 1,75 °, p = 0,005 , d _est. = 0,151), но нет существенной разницы в ширине настройки ( w разница: 0.002, равно разнице FWHM: -2,81 °, p = 0,379 , d _est = 0,806).

Рис. 5: Результаты экспериментов 3 и 4.

Последовательная зависимость (ордината) показана как функция разности направлений движения (абсцисса) между элементом предыдущего испытания и целью текущего испытания (эксперимент 3 : панели a — c , эксперимент 4: панели d — f ). Подробнее см. Рис. 2 и методы.Серийная зависимость была выявлена ​​с помощью средних групповых ошибок ответа (тонкие линии), с соответствующими заштрихованными областями, отображающими стандартную ошибку среднего группового значения. Модель DoG (показана жирными линиями) была адаптирована к ошибкам ответа для оценки систематической ошибки ответа. Сплошные линии указывают на значительную систематическую ошибку, а пунктирные линии — на незначительную. Черные закрашенные кружки и черные пунктирные линии показывают амплитуды и FWHM подходов DoG и сопровождаются символом, указывающим результат прямого сравнения оценок параметров (односторонние тесты перестановки, 20 участников на эксперимент).Звездочки указывают на значение p <0,05, а «н.с.» указывает на несущественный результат со значением p ≥ 0,05. a Серийная зависимость наблюдалась между предметами одного цвета, но не между предметами разного цвета (разница амплитуд: p = 0,005, разница ширины: p = 0,153). b Серийная зависимость наблюдалась между предметами с одинаковым пространственным положением, но не между предметами с разным пространственным положением (разница амплитуд: p <0.001, разница ширины: p = 0,154). c Серийная зависимость наблюдалась от цели предыдущего испытания, но не от предыдущего нецелевого (разница амплитуд: p = 0,003, разница ширины: p = 0,012). d Серийная зависимость наблюдалась как для предметов одного цвета, так и для разных цветов, без разницы между обоими условиями (разница амплитуд: p = 0,434, разница ширины: p = 0,284). e Серийная зависимость наблюдалась между предметами с одинаковым пространственным положением, но не между предметами с разным пространственным положением.(разница амплитуд: p = 0,005, разница ширины: p = 0,379). f Серийная зависимость наблюдалась от мишени предыдущего испытания, но не от предыдущей нецелевой (разница амплитуд: p = 0,010, разница ширины: p = 0,148). Исходные данные представлены в виде файла исходных данных.

Удивительно, но эксперимент 3 также показал, что пространственное положение влияет на последовательную зависимость, даже когда это не имеет отношения к задаче. Этот эффект был сопоставим с экспериментом 4, где пространственное положение было релевантным для задачи.Мы наблюдали значительную последовательную зависимость между элементами с одинаковым пространственным положением (амплитуда = 2,83 °, SD = 0,561 °, нижние 95% перестановок между -2,73 ° и 1,48 °, p = 0,001 , d _est = 0,528, R ² = 0,069 ; FWHM = 40,42 °), но не между стимулами с разными пространственными положениями (амплитуда = -0,67 °, SD = 0,506 °, нижние 95% перестановок между -2,11 ° и 1,26 °, p = 0.228, d _est = −0,147 , R ² = 0,014 ; FWHM = 113,32 °). Прямое статистическое сравнение показало значительную разницу между амплитудами смещения (разность амплитуд = 3,50 °, p <0,001 , d _est = 0,670), но никакой разницы между шириной настройки ( w разница: 0,018, равна разнице на полуширине: −72,90 °, p = 0,154 , d _est = 1.146). Напротив, цвет как не имеющая отношения к задаче контекстная особенность в Эксперименте 4 не влияла на серийную зависимость. Это согласуется с результатами эксперимента 2, где цвет также не имел значения. Последовательная зависимость, когда текущий элемент имел тот же цвет, что и предыдущий стимул (амплитуда = 2,23 °, SD = 0,539 °, более низкие 95% перестановок между -2,90 ° и 1,64 °, p = 0,004 , d _est = 1,369, R ² = 0.029) было сопоставимо с тем, когда они имели разные цвета (амплитуда = 2,04 °, SD = 0,671 °, ниже 95% перестановок между -2,32 ° и 1,48 °, p = 0,007 , d _est = 0,494 , R ² = 0,021 ) (разность амплитуд = 0,18 °, p = 0,434 , d _est = 0,528). То же самое было верно для ширины настройки (тот же цвет: FWHM = 42,88 °, разные цвета: FWHM = 38,78 °, w разница = -0.003, равно разнице FWHM: 4,10 °, p = 0,284, d _est = 0,374).

В совокупности пространственное положение влияло на последовательную зависимость независимо от его актуальности для задачи, тогда как цвет имел влияние только тогда, когда он был релевантным для задачи.

Результаты экспериментов 3 и 4 также хорошо соответствовали экспериментам 1 и 2 в отношении эффекта предыдущей роли. Эксперимент 3 показал значительную серийную зависимость от предыдущих целей (амплитуда = 2.86 °, SD = 0,749 °, ниже 95% перестановок между -2,55 ° и 1,47 °, p <0,001, d _est = 0,912 , R ² = 0,058; FWHM = 31,17 °), но не из предыдущих нецелевых (амплитуда = 0,28 °, SD = 0,792 °, ниже 95% перестановок между -1,54 ° и 1,16 °, p = 0,391 , d _est = 0,112 , ² = 0,002 ; FWHM = 97.99 °). Прямое статистическое сравнение показало значительную разницу амплитуд 2,58 ° ( p = 0,003 , d _est = 0,703) и значительную разницу в ширине настройки ( w разница: 0,025, равна разнице FWHM. : −66,82 °, p = 0,012 , d _est = 0,502). Мы наблюдали аналогичную картину результатов в эксперименте 4: значительная последовательная зависимость от предыдущих целей (амплитуда = 3.06 °, SD = 0,569 °, ниже 95% перестановок между -2,59 ° и 1,54 °, p <0,001, d _est = 0,905 , R ² = 0,052; FWHM = 44,379 °), но не от предыдущих нецелевых (амплитуда = 1,26 °, SD = 0,902 °, ниже 95% перестановок между -2,51 ° и 1,54 °, p = 0,096, d _est = 0,188 , ² = 0,008 ; FWHM = 34.19 °). Прямое статистическое сравнение между целями и нецелевыми показателями показало значительную разницу амплитуд 1,79 ° ( p = 0,010 , d _est = 0,648), но не было существенной разницы в ширине настройки ( w : -0,008, равно разнице FWHM: 10,60 °, p = 0,148 , d _est = 0,806).

Мы снова исследовали возможные взаимодействия, которые не дали существенных результатов (см. Дополнительный рис.1 и дополнительные таблицы 3 и 4).

Контекстная информация поддерживает последовательную зависимость нескольких визуальных объектов от эпизодов памяти

Методы

Субъекты

Пятьдесят один субъект, набранный из Франкфуртского университета Гете и Франкфуртского университета прикладных наук Фрезениуса, не участвовал в эксперименте 2, ни один из которые участвовали в эксперименте 1. Все субъекты сообщили о нормальном зрении или зрении с поправкой на нормальное. Два субъекта были исключены из окончательного анализа из-за плохого выполнения задачи (стандартное отклонение ошибки отчета> 3 стандартное отклонение среднего значения выборки).Таким образом, мы включили 49 субъектов (19 мужчин) в возрасте от 18 до 33 лет (в среднем 23,8 года). Все субъекты дали информированное согласие и получили компенсацию в размере 10 евро в час или зачет курса. Исследование было одобрено этическим комитетом медицинского факультета Университета Гете во Франкфурте-на-Майне и, следовательно, соответствовало их этическим нормам.

Процедура и стимулы

Используемая процедура и стимулы соответствовали описанным для эксперимента 1. Было только два различия. Во-первых, подсказки теперь основывались на кодировке стимулов, а не на их цвете.Номерной знак заменил квадрат фиксации, чтобы указать, какое из представленных направлений необходимо сообщить (рис. 1b). Чтобы гарантировать, что цвет стимула не дает информации о кодирующей позиции стимула, в качестве второго изменения стимулы, представленные в одном испытании, теперь могут иметь одинаковый или разные цвета. Это привело к появлению четырех возможных цветовых комбинаций в рамках испытания (красный-красный, красный-зеленый, зеленый-зеленый, зеленый-красный). Каждая из этих цветовых комбинаций встречалась одинаково часто. В половине испытаний нужно было сообщить о первом предъявленном стимуле, а в другой половине — о втором, который был сбалансирован по различным комбинациям разницы цвета и направления.Использовались три разных монитора с соотношением сторон экрана 4: 3, два с частотой обновления 60 Гц и один с частотой обновления 75 Гц, но все параметры стимула оставались постоянными. Испытуемые снова сидели на расстоянии около 50 см.

Анализ

Все этапы проведенного анализа были такими же, как и в эксперименте 1.

Результаты

Последовательная зависимость между испытаниями

Когда два объекта были закодированы в WM, и один из них был подан для отчета по порядковой позиции, мы наблюдали значительную серийная зависимость по испытаниям с амплитудой 2.00 ° (SD = 0,200 °, нижние 95% перестановок между -0,93 ° и 0,57 °, p < .001 , d _est = 1,123 , тест перестановок (n = 49 участников) ), R ² = .118 ) и FWHM 34,63 ° с максимумом кривой, расположенным под 21,44 °.

Влияние контекстных признаков

Последовательная зависимость явно модулировалась релевантной для задачи контекстной особенностью, то есть последовательным положением (рис.3Б). Сила последовательной зависимости была увеличена, когда текущий стимул был представлен в той же последовательной позиции, что и предыдущий (амплитуда = 2,33 °, SD = 0,204 °, более низкие 95% перестановок между -1,15 ° и 0,71 °, p < .001 , d _est = 1,243 , R ² = .106 ) по сравнению с тем, когда они были представлены в различных последовательных положениях (амплитуда = 1,82 °, SD = 0.200 °, ниже 95% перестановок между -0.87 ° и 0,56 °, p < .001 , d _est = 0,881 , R ² = 0,045 ) (разница амплитуд = 0,52 °, p = .009 , d _est = 0,387 ). Кроме того, мы наблюдали более широко настроенную серийную зависимость между предметами в одной и той же серийной позиции (FWHM = 44,60 °) по сравнению с разными серийными позициями (FWHM = 26.04 °) (разница w: -0,018, равна разнице FWHM: 18,56 °, p < .001 , d _est = 0,840 ).

Рисунок 3.

Результаты эксперимента 2. Последовательная зависимость (ордината) была показана как функция разности направлений движения (абсцисса) между элементом предыдущего испытания и целью текущего испытания. Подробнее см. Рисунок 1 и Методы. а) Серийная зависимость существенно не различалась между предметами одного цвета и разных цветов.б) И амплитуда, и ширина серийной зависимости были больше между изделиями с одинаковыми порядковыми позициями, чем между изделиями с разными порядковыми позициями. c) И амплитуда, и ширина последовательной зависимости были больше для предыдущих целей, чем для нецелевых.

Напротив, цвет контекстной характеристики, не имеющей отношения к задаче, не модулировал последовательную зависимость (рис. 3A). В частности, мы наблюдали сопоставимую силу последовательной зависимости, когда текущий элемент имел тот же цвет, что и предыдущий стимул (амплитуда = 2.06 °, SD = 0,195 °, ниже 95% перестановок между -1,19 ° и 0,65 °, p < .001 , d _est = 0,674 , R ² = .076 ), как если бы они имели разные цвета (амплитуда = 1,93 °, SD = 0,275 °, ниже 95% перестановок между -1,33 ° и 0,63 °, p < .001 , d _est = 0,812 , R ² = .057 ) (разность амплитуд = 0,13 °, p = . 347 , d _est = -0,065 ). То же самое справедливо и для ширины настройки (тот же цвет: FWHM = 36,00 °, разные цвета: FWHM = 33,27 °, разность ширины = -0,0003, равна разнице FWHM: 2,73 °, p = 0,228 , d _есть < 0,001 ).

Эффекты предыдущей роли

Эксперимент 2 подтвердил, что роль предмета в предыдущем испытании, т.е.е. была ли это цель или нет, сильно модулированная серийная зависимость (рис. 3C). Опять же, мы наблюдали последовательную зависимость от предыдущих целей (амплитуда = 3,46 °, SD = 0,240 °, более низкие 95% перестановок между -1,59 ° и 0,92 °, p < .001 , d _est = 1,654 , R ² = ,176 ). Однако увеличение количества испытуемых выявило привлекательную предвзятость и по сравнению с предыдущими нецелями (амплитуда = 0.60 °, SD = 0,297 °, нижние 95% перестановок между -0,62 ° и 0,44 °, p = .009 , d _est = 0,421 , R ² = . 005 ). Важно отметить, что смещение от предыдущей цели было сильнее, чем от предыдущей нецелевой (разница амплитуд: 2,86 °, p < 0,001 , d _est = 1,192 ). Кроме того, ширина настройки серийной зависимости от предыдущих целей (FWHM = 37.98 °) был шире, чем на предыдущих нецелевых (FWHM = 22,28 °) (разница w = -0,021, равна разнице FWHM: 15,70 °, p < 0,001 , d _est = 1.070 ).

Эффекты взаимодействия релевантных для задачи и не относящихся к задаче функций контекста и предыдущей роли

Мы также исследовали возможные взаимодействия между тремя противоположностями. Ни одно из вычисленных взаимодействий не было значимым. Для амплитуд наблюдается один слабый тренд ( p = .111 , d _est = -0,140 ), что позволяет предположить, что наблюдаемое увеличение амплитуды между предметами с одинаковым порядковым положением было более заметным, когда предыдущий предмет был нецелевым (разница амплитуд: 1,12 °), чем когда это была цель (разница амплитуд: 0,48 °). Для нецелевых элементов несовпадение положения на самом деле может даже привести к изменению наблюдаемого смещения (нецелевое положение совпадающее: амплитуда 0,61 °, неконгруэнтное положение нецелевого объекта: -0.Амплитуда 51 °). Все остальные взаимодействия были далеки от достижения значимости как по амплитуде (минимум p = , 610 ), так и по ширине (минимум p = 0,464 ).

Сводка результатов

Эксперимент 2 направлен на решение двух открытых вопросов: во-первых, релевантные для задачи и не относящиеся к задаче контекстные функции по-разному модулируют последовательную зависимость содержимого объекта, и, во-вторых, возникает ли последовательная зависимость для нецелевых объектов из предыдущих испытаний. .Мы обнаружили, что цвет, который служил контекстной особенностью задачи в Эксперименте 1, но не имел отношения к задаче в Эксперименте 2, не модулировал последовательную зависимость. Точно так же релевантная для задачи серийная позиция в Эксперименте 2 влияла на амплитуду последовательной зависимости, чего не было в Эксперименте 1, где серийная позиция не имела значения для задачи. Однако, в отличие от цвета, серийное положение влияло на ширину настройки серийной зависимости независимо от того, было ли оно актуальным для задачи или нет. Что касается влияния предыдущей роли на серийную зависимость, эксперимент 2 с увеличенным числом испытуемых выявил привлекательную предвзятость также и от предыдущих нецелевых.Однако как амплитуда, так и ширина настройки последовательной зависимости была заметно меньше для предыдущих нецелевых объектов, чем для целей.

Общее обсуждение

Текущие модели предполагают, что объекты в WM состоят из связанного содержимого и контекстных функций, которые устанавливаются заново в каждом эпизоде ​​памяти. Однако недавние исследования показали, что характеристика контента одного объекта, закодированного в WM, выборочно привлекалась к аналогичной характеристике контента в прошлом представлении объекта. Это явление, получившее название серийной зависимости, вызвало большой исследовательский интерес (Kiyonaga et al., 2017). Но, поскольку мы обычно храним в WM несколько объектов, остается неясным, взаимодействуют ли несколько объектов в эпизодах памяти. Чтобы ответить на этот вопрос, мы провели два эксперимента, в которых участники запоминали два последовательно представленных направления движения (S1 и S2), которые различались по цвету. После короткой задержки цветовой сигнал (красный или зеленый; эксперимент 1) или последовательный позиционный сигнал (первый или второй стимул; эксперимент 2) указывали, какой стимул направления движения следует сообщать. Таким образом, мы могли оценить влияние трех факторов на серийную зависимость: соответствие контекстных характеристик в испытаниях (цвет или порядковое положение), релевантность задачи контекстных характеристик и роль объекта в предыдущем испытании.Мы обнаружили, что все эти факторы поддерживают последовательную зависимость в ситуациях, когда несколько объектов закодированы в WM. В частности, мы наблюдали более сильную последовательную зависимость между элементами, которые обладали одними и теми же характеристиками контекста, важными для задачи, в разных испытаниях. Более того, серийное положение отчасти способствовало серийной зависимости, даже когда это была не относящаяся к задаче контекстная особенность, тогда как нерелевантный для задачи цвет не имел такого эффекта. В-третьих, независимо от контекста, в предыдущем испытании привлекательная предвзятость была сильнее в отношении целевого элемента.В совокупности наши результаты показывают, что последовательная зависимость, основанная на подобии контента, усиливается между объектами, которые имеют одни и те же релевантные для задачи контекстные функции и которые внутренне выбраны в качестве целевых объектов.

В большинстве предыдущих исследований серийной зависимости между испытаниями в WM нужно было кодировать только один элемент на испытание. Напротив, настоящее исследование показало, что серийная зависимость также возникает, когда два элемента в испытании присутствовали и закодированы в WM, повторяя недавние результаты из нашей лаборатории (Czoschke et al., 2019). Важно отметить, что мы также повторили вывод о том, что серийная зависимость между испытаниями особенно ярко выражена для целевых элементов, которые были задокументированы для отчета в предыдущем испытании. Ретро-метки подразумевают, что цели были внутренне выбраны в фокусе внимания. Напротив, предыдущие исследования показали усиление последовательной зависимости для заранее запрограммированных целей, то есть в результате внешнего манипулирования выбором и кодированием внимания (Fischer & Whitney, 2014). Взятые вместе, эти результаты показывают, что как внешнее, так и внутреннее внимание сильно способствуют серийной зависимости.Интересно, что настоящий эксперимент 2 с увеличенным числом субъектов выявил серийную зависимость также и для нецелевых, хотя и с явно уменьшенной амплитудой по сравнению с целями. Поскольку как цели, так и нецелевые из предыдущего испытания не имели отношения к текущему испытанию, этот результат указывает на то, что приоритезация внимания в предыдущем испытании сильно модулирует величину серийной зависимости, не являясь необходимым предварительным условием для ее возникновения.

Помимо влияния внимания, еще одним ключевым свойством последовательной зависимости является то, что она действует избирательно между объектами со схожим содержанием, что отражается в стереотипном профиле настройки, наблюдаемом для ряда различных функций контента, таких как ориентация (Fischer & Whitney, 2014), лица (Либерман и др., 2014), пространственное положение (Bliss et al., 2017), ансамблевые представления (Manassi et al., 2017) или направление движения (Czoschke et al., 2019). Основываясь на этом свойстве, Фишер и Уитни (2014) предположили, что последовательная зависимость уменьшает небольшие различия между последовательными функциями контента, чтобы поддерживать впечатление согласованной среды. Новым открытием настоящего исследования было то, что, помимо сходства содержания, контекстные особенности также оставляют следы в WM и, таким образом, помогают связать соответствующие объекты в эпизодах памяти.В частности, мы наблюдали более сильную и более широко настроенную последовательную зависимость между направлениями движения с одинаковым цветом (эксперимент или последовательное положение (эксперимент 2). Предыдущие исследования с использованием только одного стимула на испытание дали противоречивые результаты относительно роли контекстных характеристик, таких как пространственное положение для серийной зависимости (Fischer & Whitney, 2014; Fritsche et al., 2017). Настоящий дизайн, требующий выборочного отчета по одному из двух пунктов за испытание, должен был усилить связь между функциями контента и контекста, тем самым усилив влияние контекста по серийной зависимости.Этот вывод подтверждает предположение, что последовательная зависимость указывает на непрерывность поля в изменяющейся среде, которая способствует стабильности представлений объекта во времени.

Наблюдаемая модуляция последовательной зависимости как сходством содержания, так и соответствием контекста предполагает, что отдельные особенности объекта представлены в WM как связанные до некоторой степени. Это соответствует структурам, которые предполагают организацию WM со встроенными многофункциональными объектами (Brady et al., 2011; Удача и Фогель, 1997; Оберауер и Лин, 2017). Определение элемента WM как комбинации содержимого и функций контекста близко соответствует концепции объектных файлов (Kahneman, Treisman, & Gibbs, 1992; Treisman, 1986). Объектный файл содержит различные функции объекта, которые образуют временное представление, что позволяет нам отслеживать объект во времени. Идентификация объекта должна оставаться стабильной и защищенной от небольших изменений внешнего вида объекта, вызванных, например, движением или изменением условий освещения.Хотя первичные исследования показали, что особенности объекта распознаются быстрее для ранее представленных объектов (Noles, Scholl, & Mitroff, 2005), механизм, позволяющий отслеживать объекты во времени, остается неизвестным. Фишер и Уитни (2014) предложили серийную зависимость как механизм, лежащий в основе непрерывности объектов. Однако между эпизодами памяти с множеством релевантных объектов последовательная зависимость будет служить временной интеграции только в том случае, если она работает в режиме объектного файла, связывая соответствующие пакеты содержимого и контекстных функций.Наши результаты показывают, что контекстное соответствие объектов явно способствует последовательной зависимости, таким образом подтверждая интерпретацию, что последовательная зависимость является механизмом, подходящим для временной интеграции представлений объектов во времени.

В то время как контекст, релевантный задаче, постоянно усиливает последовательную зависимость, эффект нерелевантного контекста различается в разных экспериментах. В эксперименте 1 мы обнаружили, что не относящаяся к задаче порядковая позиция изменяет ширину настройки последовательной зависимости.Напротив, в эксперименте 2 не было такого эффекта для цвета, не имеющего отношения к задаче. Одно из объяснений может заключаться в том, что серийное положение в большей степени автоматически интегрируется в представление объекта, чем цвет, хотя последний является более заметной визуальной особенностью. Это связано с важностью пространственно-временной информации для определения объекта (Treisman, 1986). Кроме того, он отражает важность последовательной позиции как контекстной особенности, независимо от ее актуальности для задачи. Последовательный порядок событий, т.е.е., предъявление стимулов, определяет порядковое положение предмета и, таким образом, определяет временную структуру испытания. Следовательно, временная информация может иметь решающее значение для представления предметов, особенно в случае последовательно представленных предметов в одной и той же пространственной позиции (Schneegans & Bays, 2018). Взятые вместе, будущие исследования должны исследовать роль временного положения для представлений WM более глубоко.

Кроме того, мы наблюдали различные эффекты релевантности задачи на амплитуду смещения для обеих характеристик контекста.Что касается цвета, наши результаты показывают, что последовательная зависимость была подавлена ​​между предметами разного цвета, когда она была релевантной задаче (амплитуда = 0,87 °), по сравнению с тем, когда она была несущественной для задачи (амплитуда = 1,93 °), тогда как она была довольно похожей для предметов из того же цвета, когда он был релевантным или не относящимся к задаче (амплитуда 2,32 ° и 2,06 °, соответственно). Для серийной позиции, напротив, актуальность задачи увеличивала амплитуду последовательной зависимости между предметами с одинаковой серийной позицией (амплитуда = 2.33 °), в отличие от того, когда он не относился к задаче (амплитуда = 1,56 °), и был аналогичным для предметов с разными порядковыми позициями, когда он был релевантным или нерелевантным для задачи (амплитуда 1,82 ° и 1,76 °, соответственно). Это указывает на то, что актуальность задачи увеличивала амплитуду между предметами с одинаковым порядковым положением, тогда как она подавляла амплитуду между предметами разного цвета. Это еще больше усиливает интерпретацию того, что цвет и порядковое положение могут быть двумя качественно разными контекстными характеристиками.

Большое количество исследований WM показало, что, когда зонд не входил в состав набора, запомненного в настоящее время, а из набора, представленного в предыдущем испытании, время реакции было больше, а точность распознавания снижалась (см. Jonides & Nee, 2006 , для обзора). Это явление называется проактивным вмешательством и чаще всего исследуется с использованием вербальных стимулов (например, Jonides, Smith, Marshuetz, Koeppe & Reuter-Lorenz, 1998; Keppel & Underwood, 1962). Проактивное вмешательство наблюдалось также для визуальных элементов, таких как цвета или формы.Здесь это было особенно заметно, когда прошлые и текущие предметы были представлены в одном и том же пространственном месте (Makovski & Jiang, 2008). Точно так же в задачах последовательного отзыва участники часто неправильно сообщали элементы из предыдущих списков (так называемые вторжения) в одной и той же позиции отзыва в ходе испытаний (например, Henson, 1999). И проактивное вмешательство, и серийная зависимость описывают влияние предыдущих эпизодов WM на текущие, что привело к предположению, что оба могут возникать из одного и того же основного механизма (Kiyonaga et al., 2017). Наши результаты показывают, что серийная зависимость поддерживается соответствующими контекстными особенностями в разных испытаниях. Поскольку то же самое верно и для проактивного вмешательства (Henson, 1999; Makovski & Jiang, 2008), это подтверждает возможность того, что последовательная зависимость и проактивное вмешательство отражают один и тот же механизм. С другой стороны, эта гипотеза подвергается сомнению из-за важных различий между обоими явлениями. Проактивные эффекты вмешательства возникают из-за того, что предмет из предыдущего испытания ошибочно назначен набору предметов текущего испытания.Это указывает на то, что привязка между элементом и его пробным контекстом была неправильной. Напротив, последовательная зависимость описывает интеграцию предыдущего в текущую характеристику содержимого объекта, чему способствует схожесть содержимого и соответствие контекста, а не ошибочный отзыв предыдущего объекта. Более того, в большинстве исследований проактивного вмешательства наблюдаемые эффекты связаны с ранее закодированными, но не протестированными элементами, то есть нецелевыми. Bäuml и Kliegl (2013) даже показали, что элементы тестирования из предыдущего списка устраняют проактивное вмешательство в последующий список.С другой стороны, серийная зависимость в основном возникает из-за цели предыдущего исследования, как показывают наши результаты вместе с предыдущими (Czoschke et al., 2019; Fischer & Whitney, 2014). Более того, проактивное вмешательство обычно интерпретируется как неисправность, которую необходимо преодолеть, тогда как последовательная зависимость считается полезным механизмом временного сглаживания. Наши результаты подтверждают идею о том, что механизм, лежащий в основе последовательной зависимости, является полезным, поскольку он связывает объекты во времени, уменьшая небольшие различия между их представлениями.Хотя это было бы полезно в естественной среде, это может привести к вредным результатам в искусственных условиях, что приведет к систематическим ошибкам или снижению производительности в исследованиях последовательной зависимости или упреждающего вмешательства, соответственно. В частности, было обнаружено, что проактивное вмешательство отрицательно коррелирует как с мощностью WM (Mecklinger, Weber, Gunter, & Engle, 2003), так и с интеллектом (Braver, Gray, & Burgess, 2007). Если эффекты интерференции являются результатом в целом благоприятного механизма, люди с более высокими возможностями WM или подвижным интеллектом могут лучше стратегически контролировать этот механизм.Взятые вместе, проактивное вмешательство и последовательная зависимость различаются в отношении их концептуального объяснения и того, возникают ли они из предыдущих целей или нецелевых, но оба описывают влияние прошлых событий памяти на текущие, которое может модулироваться конгруэнтностью контекста объектов через время. Следовательно, необходимы дополнительные исследования, чтобы разобраться в том, проистекают ли эти явления из одного и того же основного механизма и в какой степени.

До сих пор этап обработки, на котором возникает серийная зависимость, оставался неясным.В то время как некоторые исследования предлагали стадию восприятия (Cicchini, Mikellidou, & Burr, 2017; Fischer & Whitney, 2014; Fornaciai & Park, 2018; Manassi et al., 2017; St. John-Saaltink, Kok, Lau, & de Lange) , 2016), другие предоставили доказательства процесса, связанного с памятью или решениями (Bliss et al., 2017; Fritsche et al., 2017; Papadimitriou, Ferdoash, & Snyder, 2015; Pascucci et al., 2019). Настоящие результаты подтверждают гипотезу о последовательной зависимости как о механизме, основанном на памяти или принятии решений.Мы заметили, что влияние обеих исследуемых контекстных характеристик на серийную зависимость в значительной степени зависит от актуальности этих функций для задачи. Кроме того, чисто визуальная контекстная функция, то есть цвет, в большей степени зависит от релевантности задачи, чем последовательная позиция. Важно отметить, что последняя особенность не присуща визуальному представлению стимула, а возникает только в контексте испытания. Взятые вместе, эти наблюдения выступают против исключительно перцептивной основы серийной зависимости. Будущие исследования нейронных основ этого механизма могут пролить свет на стадию обработки, на которой возникает последовательная зависимость.

Наше исследование показало, что представления в WM смещены в сторону предыдущих представлений, особенно тех, которые были целями и имели соответствующие контекстные особенности, относящиеся к задаче. Это позволяет по-новому взглянуть на организацию обработки объектов. По-видимому, привязка характеристик содержания и контекста не полностью стирается после эпизода воспоминания, но до некоторой степени переносится на последующие эпизоды, указывая на механизм, который выборочно интегрирует соответствующие представления многофункциональных объектов с течением времени.

Последовательная корреляция — обзор, использование в финансовом моделировании и пример

Что такое последовательная корреляция?

Последовательная корреляция — это статистический термин, используемый для описания взаимосвязи, в частности корреляции, между текущим значением переменной и запаздывающим значением той же переменной из более ранних периодов времени.

Последовательная корреляция, также называемая автокорреляцией Автокорреляция Автокорреляция, также известная как последовательная корреляция, относится к степени корреляции одних и тех же переменных между двумя последовательными интервалами времени., часто используется финансовыми аналитиками для прогнозирования будущих движений цены ценных бумаг, таких как акции, на основе предыдущих движений цен.

Корреляция измеряет силу взаимосвязи между переменными, а последовательная корреляция определяет взаимосвязь, если таковая имеется, между одной и той же переменной, измеренной в разные периоды времени.

Если выясняется, что текущая стоимость ценной бумаги последовательно коррелирует с ее предыдущими значениями, то эту корреляцию можно использовать для прогнозирования возможных будущих значений.

Сводка

• Последовательная корреляция измеряет взаимосвязь между текущим значением переменной и значениями той же переменной за предыдущие периоды времени.
• Исследование последовательных корреляций обычно используется финансовыми аналитиками при создании финансовых моделей, помогающих прогнозировать вероятные будущие цены на акции или другие финансовые ценные бумаги.
• Положительные последовательные корреляции указывают на то, что значения, вероятно, изменятся в будущих периодах времени таким же образом или в том же направлении, что и в недавние прошедшие периоды времени; Отрицательные последовательные корреляции указывают на то, что значения, вероятно, будут двигаться в противоположном направлении в будущих периодах времени по сравнению с тем, как значения перемещались в недавние прошлые периоды.

Измерение последовательных корреляций

Последовательные корреляции, если они существуют, могут быть либо положительными , либо отрицательными .

• Положительные последовательные корреляции указывают на то, что изменения стоимости между текущей ценой ценной бумаги Безопасность Ценная бумага является финансовым инструментом, обычно любым финансовым активом, которым можно торговать. Характер того, что можно и что нельзя называть ценной бумагой, обычно зависит от юрисдикции, в которой торгуются активы.и будущие цены, вероятно, будут аналогичны изменениям стоимости между недавними прошлыми ценами и текущей ценой.
• Отрицательная последовательная корреляция указывает на то, что изменения значений между текущей ценой и будущими ценами, вероятно, будут двигаться в противоположном направлении, поскольку значение изменяется между прошлыми ценами и текущей ценой.

Когда переменная текущей цены ценной бумаги и ее цены в предыдущий период времени демонстрируют положительную последовательную корреляцию, они показывают так называемое среднее отвращение.

Отклонение от среднего значения указывает на то, что изменения цены ценной бумаги склонны следовать трендам и что с течением времени они будут показывать более высокие стандартные отклонения, чем в случае отсутствия корреляции.

Существует множество сложных статистических формул, которые можно использовать для измерения последовательной корреляции; однако большинство формул рассчитывают последовательную корреляцию со значениями от -1 до +1.

Нулевое значение последовательной корреляции указывает на отсутствие корреляции.Другими словами, не существует наблюдаемых отношений или закономерностей между текущим значением переменной и ее значением в предыдущие периоды времени. Значения, близкие к +1, указывают на положительную последовательную корреляцию, тогда как значения между нулем и -1 указывают на отрицательную последовательную корреляцию.

Использование последовательной корреляции в финансовом моделировании

Выявление и реализация использования последовательной корреляции при построении финансовых моделей Что такое финансовая модель? Финансовая модель представляет собой представление прошлых и будущих результатов компании на основе ее активов и операций.Узнайте: что такое финансовая модель? становится все более популярным с начала широкого использования компьютерных технологий в 1980-х годах.

Инвестиционные банки и другие финансовые учреждения в настоящее время регулярно включают исследование последовательных корреляций, чтобы помочь улучшить модели прогнозирования доходности инвестиций путем выявления закономерностей, которые могут возникать в изменении цен с течением времени.

Повышая точность финансовых моделей, использование мер последовательной корреляции может помочь максимизировать отдачу от инвестиций, снизить инвестиционный риск или и то, и другое.

Изучение последовательных корреляций на самом деле зародилось не в индустрии финансовых услуг — оно зародилось в мире инженерии. Первыми исследованиями последовательных корреляций были исследования того, как сигналы, такие как сигналы радиовещания, менялись в течение последовательных периодов времени.

После того, как такие исследования оказались плодотворными, экономисты и финансовые аналитики постепенно начали рассматривать последовательные корреляции между значениями цен на ценные бумаги и различными экономическими показателями, такими как процентные ставки или валовой внутренний продукт (ВВП).

Корреляции можно измерить с помощью формулы = КОРРЕЛЬ Функция КОРРЕЛЬ Функция КОРРЕЛЬ относится к категории Статистических функций Excel. Он рассчитает коэффициент корреляции между двумя переменными. Как финансовый аналитик, функция CORREL очень полезна, когда мы хотим найти корреляцию между двумя переменными, например, корреляцию между a в Excel.

Пример — определение моментальных акций

Пример того, как серийная корреляция может использоваться для прогнозирования будущих движений цен ценной бумаги, можно найти в импульсных акциях.

Акции Momentum — это акции, которые исторически демонстрировали движения цен, которые выявляют устойчивые тенденции. То есть, как только цена акции начинает двигаться в одном направлении, она имеет тенденцию набирать обороты и продолжать движение в том же направлении в течение последовательных периодов времени.

Акции моментума могут быть идентифицированы, потому что они будут демонстрировать положительную серийную корреляцию. Можно показать, что текущая цена акции имеет положительную корреляцию с ценой акции в предыдущие периоды времени.

Инвестор может использовать эти знания для получения прибыли от покупки идентифицированных моментумных акций, как только они начинают демонстрировать ценовой тренд.

Инвестор покупает акции, исходя из предположения, что будущие изменения цен будут иметь тенденцию напоминать недавние прошлые изменения цен — другими словами, акция будет продолжать иметь тенденцию в течение по крайней мере некоторого периода времени в будущем.

Дополнительные ресурсы

CFI является официальным поставщиком сертификации коммерческого банковского и кредитного аналитика (CBCA) ™ CBCA®. Аккредитация коммерческого банковского и кредитного аналитика (CBCA) ™ является мировым стандартом для кредитных аналитиков, охватывающим финансы, бухгалтерский учет и т.д. кредитный анализ, анализ денежных потоков, моделирование ковенантов, погашение ссуд и многое другое.программа сертификации, призванная превратить любого в финансового аналитика мирового уровня.

Чтобы продолжать изучать и развивать свои знания в области финансового анализа, мы настоятельно рекомендуем дополнительные ресурсы, указанные ниже:

• DecouplingDecouplingDecoupling представляет собой создание пробелов. В финансах разделение происходит, когда разные классы активов или рынки обычно демонстрируют
• Отрицательная корреляция Отрицательная корреляция Отрицательная корреляция — это связь между двумя переменными, которые движутся в противоположных направлениях.Другими словами, когда переменная A увеличивается, переменная B уменьшается. Отрицательная корреляция также известна как обратная корреляция. См. Примеры, диаграммы и
• Множественная линейная регрессия Множественная линейная регрессия Множественная линейная регрессия относится к статистическому методу, используемому для прогнозирования результата зависимой переменной на основе значений независимых переменных
• Финансовое прогнозирование Финансовое прогнозирование Финансовое прогнозирование — это процесс оценки или прогнозирования того, как бизнес будет работать в будущем.Это руководство по построению финансового прогноза

Определение последовательной корреляции

Что такое последовательная корреляция?

Последовательная корреляция происходит во временном ряду, когда переменная и запаздывающая версия самой себя (например, переменная в моменты времени T и в момент T-1) наблюдаются коррелированными друг с другом в течение периодов времени. Повторяющиеся паттерны часто показывают последовательную корреляцию, когда уровень переменной влияет на ее будущий уровень. В финансах эта корреляция используется техническими аналитиками, чтобы определить, насколько хорошо прошлая цена ценной бумаги предсказывает будущую цену.

Последовательная корреляция похожа на статистические концепции автокорреляции или корреляции с задержкой.

Ключевые выводы

• Последовательная корреляция — это взаимосвязь между заданной переменной и отстающей версией самой себя за различные интервалы времени.
• Он измеряет взаимосвязь между текущим значением переменной с учетом ее прошлых значений.
• Переменная с последовательной корреляцией указывает на то, что она не может быть случайной.
• Технические аналитики проверяют прибыльные модели ценной бумаги или группы ценных бумаг и определяют риск, связанный с инвестиционными возможностями.

Объяснение последовательной корреляции

Последовательная корреляция используется в статистике для описания взаимосвязи между наблюдениями одной и той же переменной за определенные периоды. Если серийная корреляция переменной измеряется как ноль, корреляции нет, и каждое из наблюдений не зависит друг от друга. И наоборот, если серийная корреляция переменной смещается в сторону единицы, наблюдения последовательно коррелируются, и на будущие наблюдения влияют прошлые значения.По сути, переменная с последовательной корреляцией имеет закономерность и не является случайной.

Условия ошибки возникают, когда модель не является полностью точной и приводит к разным результатам в реальных приложениях. Когда члены ошибки из разных (обычно смежных) периодов (или наблюдений сечения) коррелированы, член ошибки последовательно коррелируется. Последовательная корреляция возникает в исследованиях временных рядов, когда ошибки, связанные с данным периодом, переносятся на будущие периоды. Например, при прогнозировании роста дивидендов по акциям завышенная оценка за один год приведет к завышению оценок в последующие годы.

Последовательная корреляция может сделать моделируемые торговые модели более точными, что помогает инвестору разработать менее рискованную инвестиционную стратегию.

Технический анализ использует меры последовательной корреляции при анализе структуры ценной бумаги. Анализ полностью основан на движении цены акции и соответствующем объеме, а не на фундаментальных показателях компании. Специалисты, занимающиеся техническим анализом, если они правильно используют последовательную корреляцию, идентифицируют и подтверждают прибыльные модели или ценные бумаги или группу ценных бумаг и возможности спотового инвестирования.

Концепция последовательной корреляции

Последовательная корреляция первоначально использовалась в технике для определения того, как сигнал, такой как компьютерный сигнал или радиоволна, изменяется по сравнению с самим собой во времени. Эта концепция приобрела популярность в экономических кругах, поскольку экономисты и практики эконометрики использовали ее для анализа экономических данных с течением времени.

Почти все крупные финансовые учреждения теперь имеют в штате количественных аналитиков, известных как кванты. Эти аналитики финансовой торговли используют технический анализ и другие статистические выводы для анализа и прогнозирования фондового рынка.Эти разработчики моделей пытаются определить структуру корреляций для улучшения прогнозов и потенциальной прибыльности стратегии. Кроме того, определение структуры корреляции улучшает реалистичность любого смоделированного временного ряда на основе модели. Точное моделирование снижает риск инвестиционных стратегий.

Кванты являются неотъемлемой частью успеха многих из этих финансовых учреждений, поскольку они предоставляют модели рынка, которые затем организация использует в качестве основы для своей инвестиционной стратегии.

Последовательная корреляция изначально использовалась в обработке сигналов и системном проектировании для определения того, как сигнал меняется с течением времени. В 1980-х годах экономисты и математики поспешили на Уолл-стрит, чтобы применить эту концепцию для прогнозирования цен на акции.

Последовательная корреляция между этими квантами определяется с помощью теста Дарбина-Ватсона (DW). Корреляция может быть как положительной, так и отрицательной. Цена акций, показывающая положительную серийную корреляцию, имеет положительный паттерн.Ценная бумага с отрицательной серийной корреляцией со временем оказывает на себя негативное влияние.

(PDF) Последовательная зависимость в визуальном восприятии

22 Светс, Дж. А. и Грин, Д. М. Последовательные наблюдения людьми-наблюдателями

сигналов в шуме. Теория информации. Лондон: Баттервортс, 221-242

(1961).

23 Малжкович В. и Накаяма К. Подготовка всплывающих окон: I. Роль функций.

Память и познание 22, 657-672 (1994).

24 Кристьянссон, Á. И Кампана, Г. Где восприятие встречается с памятью: обзор повторения прайминга в задачах визуального поиска

. Внимание, восприятие и

Психофизика 72, 5-18 (2010).

25 Трейсман, А. и Канеман, Д. Накопление информации в

объектных файлах. Бюллетень Психономического общества 21, 354-354 (1983).

26 Гибсон, Дж. И Раднер, М. Адаптация, последействие и контраст в восприятии

наклонных линий.I. Количественные исследования. Journal of Experimental

Psychology 20, 453-467 (1937).

27 Гибсон, Дж. Дж. Адаптация, последствия и контраст в восприятии

наклонных линий. II. Одновременный контраст и ограничение площади эффекта после-

. Журнал экспериментальной психологии 20, 553-569 (1937).

28 Спайви, М. и Спирн, М. Селективное визуальное внимание модулирует последействие прямого наклона.

. Внимание, восприятие и психофизика 62, 1525-1533 (2000).

29 Knapen, T., Rolfs, M., Wexler, M. & Cavanagh, P. Система отсчета

— последействие наклона. J Vis 10 (2010).

30 Маунселл, Дж. Х. и Треу, С. Основанное на особенностях внимание в зрительной коре.

Тенденции в неврологии 29, 317-322 (2006).

31 Stocker, A. & Simoncelli, E. in Advances in Neural Information Processing

Systems Vol. 18 (редакторы Y. Weiss, B. Schölkopf и J. Platt) 1291-1298 (MIT

Press, 2006).

32 Сасаки Ю., Нанез Дж. Э. и Ватанабе Т. Развитие зрительного восприятия

Обучение и пластичность. Nature Reviews Neuroscience 11, 53-60 (2009).

33 Fiser, J. z. И Аслин Р. Н. Статистическое изучение временной структуры

более высокого порядка на основе последовательностей визуальных форм. Journal of Experimental

Психология: обучение, память и познание 28, 458 (2002).

34 Шопен А. и Мамасян П. Прогностические свойства визуальной адаптации.

Current Biology 22, 622-626 (2012).

35 Канеман Д. и Трейсман А. в Разновидностях внимания (ред. Р.

,

Парусураман и Д. Р. Дэвис) 29-61 (Academic Press, 1984).

36 Канеман Д., Трейсман А. и Гиббс Б. Дж. Обзор объектных файлов

— Объектно-ориентированная интеграция информации. Когнитивная психология 24, 175-

219 (1992).

37 Нолес, Н. С., Шолль, Б. Дж. И Митрофф, С. Р. Постоянство объектного файла

представлений.