Чем отличается соединение звездой от треугольника. Как выбрать оптимальную схему подключения трехфазного двигателя. Какие преимущества и недостатки у каждого типа соединения. Как снизить пусковые токи при запуске мощных электродвигателей.
Основные схемы соединения обмоток трехфазных двигателей
Для подключения трехфазных асинхронных электродвигателей используются две основные схемы соединения обмоток статора:
- Звезда (Y)
- Треугольник (Δ)
Каждая из этих схем имеет свои особенности, преимущества и недостатки. Выбор оптимального варианта зависит от характеристик двигателя, параметров питающей сети и условий эксплуатации.
Соединение звездой: особенности и применение
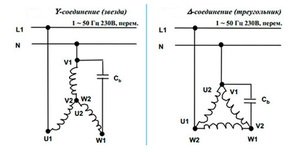
При соединении обмоток звездой все концы фазных обмоток объединяются в общую нейтральную точку. Напряжение подается на начала обмоток.
Основные характеристики соединения звездой:
- Обеспечивает более плавный пуск двигателя
- Снижает пусковые токи примерно в 3 раза
- Уменьшает пусковой момент в 3 раза
- Ограничивает мощность двигателя (примерно на 40% ниже номинальной)
Соединение звездой применяется в следующих случаях:
- Для двигателей большой мощности (свыше 5-7 кВт)
- При питании от сети 380 В
- Когда требуется снизить пусковые токи
- Для плавного пуска механизмов с большой инерционной нагрузкой
Соединение треугольником: когда оно эффективно
При соединении обмоток треугольником конец каждой обмотки соединяется с началом следующей, образуя замкнутый контур. Напряжение подается на вершины треугольника.
Ключевые особенности соединения треугольником:
- Обеспечивает полную мощность двигателя
- Создает максимальный пусковой момент
- Приводит к высоким пусковым токам (в 5-7 раз выше номинального)
- Дает более резкий пуск двигателя
Соединение треугольником эффективно в таких ситуациях:
- Для двигателей малой и средней мощности (до 5-7 кВт)
- При питании от сети 220 В
- Когда требуется максимальный пусковой момент
- Для механизмов с небольшой инерционной нагрузкой
Как выбрать оптимальную схему подключения
При выборе схемы соединения обмоток трехфазного двигателя следует учитывать несколько ключевых факторов:
- Номинальное напряжение двигателя и питающей сети
- Мощность электродвигателя
- Характер нагрузки на валу (инерционная, постоянная и т.д.)
- Требования к пусковому моменту
- Ограничения по пусковым токам
Общие рекомендации по выбору схемы:

- Двигатели до 5-7 кВт обычно подключают треугольником
- Мощные двигатели от 5-7 кВт — звездой
- При питании 220 В — треугольником
- При питании 380 В — звездой
- Для плавного пуска — звездой
- Для максимального момента — треугольником
Способы снижения пусковых токов мощных электродвигателей
Высокие пусковые токи при прямом пуске мощных двигателей могут вызвать проблемы в питающей сети. Для их ограничения применяются следующие методы:
- Пуск через автотрансформатор (снижение напряжения)
- Использование устройств плавного пуска
- Применение частотных преобразователей
- Пуск с переключением со звезды на треугольник
Последний способ является наиболее простым и экономичным. При запуске обмотки соединяются звездой, что снижает пусковой ток. После выхода на номинальные обороты происходит переключение на треугольник для работы на полной мощности.
Переключение со звезды на треугольник: принцип работы
Схема пуска двигателя с переключением со звезды на треугольник работает следующим образом:
- При запуске обмотки соединяются звездой через пускатель
- Двигатель разгоняется до 80-90% номинальной скорости
- Срабатывает реле времени (обычно 5-10 секунд)
- Происходит кратковременное отключение питания
- Обмотки переключаются на соединение треугольником
- Двигатель выходит на номинальный режим работы
Такая схема позволяет снизить пусковой ток в 3 раза по сравнению с прямым пуском. При этом обеспечивается плавный разгон и возможность работы на полной мощности.
Преимущества и недостатки переключения со звезды на треугольник
Основные плюсы данного метода пуска:
- Простота и низкая стоимость
- Значительное снижение пусковых токов
- Уменьшение нагрузки на питающую сеть
- Плавный разгон двигателя
- Возможность работы на полной мощности
К недостаткам можно отнести:
- Кратковременный провал момента при переключении
- Возможность применения только для двигателей с выведенными концами обмоток
- Необходимость использования дополнительной пусковой аппаратуры
Тем не менее, метод переключения со звезды на треугольник остается одним из самых распространенных способов пуска мощных трехфазных двигателей.
Заключение
Выбор схемы соединения обмоток трехфазного двигателя существенно влияет на его пусковые и рабочие характеристики. Правильное применение схем звезда и треугольник позволяет оптимизировать работу электропривода под конкретные условия эксплуатации. Для мощных двигателей эффективным решением является комбинированный пуск с переключением со звезды на треугольник.
Чем отличается звезда от треугольника
В трехфазных цепях обычно применяется два типа соединения обмоток трансформаторов, электрических приёмников и генераторов. Одно из этих соединений носит название звезда, другое — треугольник. Рассмотрим подробнее, что это за соединения и чем они отличаются друг от друга.
Что такое звезда и треугольник
Соединение в звезду подразумевает под собой такое соединение, в котором все рабочие концы фазных обмоток объединяются в один узел, называемый нулевой или нейтральной точкой и обозначается буквой O.
Соединение в треугольник представляет собой схему, при которой фазные обмотки генератора соединяются таким образом, что начало одной из них соединяется с концом другой.
Разница между звездой и треугольником
В чем же разница между соединением звездой и треугольником? Различие в указанных схемах состоит в соединении концов обмоток генератора электродвигателя. В схеме «звезда», все концы обмоток соединяются вместе, тогда как в схеме «треугольник»конец одной фазной обмотки монтируется с началом следующей.
Кроме принципиальной схемы сборки, электродвигатели с фазными обмотками, соединенными звездой, функционируют значительно мягче, чем двигатели, имеющие соединение фазных обмоток в треугольник. Но при соединении звездой электродвигатель не имеет возможности развивать свою полную паспортную мощность. Тогда как, при соединении фазных обмоток в треугольник двигатель всегда работает на полную заявленную мощность, которая почти в полтора раза выше, чем при соединении в звезду. Большим недостатком соединения треугольником являются очень большие величины пусковых токов.
TheDifference.ru определил, что отличие соединения звездой от соединения треугольником заключается в следующем:
- В схеме соединения звезда концы обмоток монтируются в один узел.
- В схеме соединения треугольник конец одной обмотки монтируется с началом следующей обмотки.
- Электродвигатель с обмотками, соединенными звездой работает более плавно, чем двигатель с соединением в треугольник.
- При соединении звездой мощность двигателя всегда ниже паспортной.

- При соединении в треугольник мощность двигателя почти в полтора раза выше, чем при соединении в звезду.Подробнее: http://thedifference.ru/chem-otlichaetsya-soedinenie-zvezda-ot-treugolnika/
Подключение электродвигателя звездой и треугольником (видео)
Асинхронные двигатели обладают многими преимуществами в работе. Это надёжность, большая мощность, хорошая производительность. Подключение электродвигателя звездой и треугольником обеспечивают его стабильную эксплуатацию.
В основе электромотора выделяют две основные части: крутящийся ротор и статичный статор. Оба имеют в структуре набор токопроводящих обмоток. Электрообмотки неподвижного элемента, расположены в пазах магнитного провода на расстоянии 120 градусов. Все окончания обмоток выводятся в электрораспределительный блок, там фиксируются. Контакты пронумерованы.
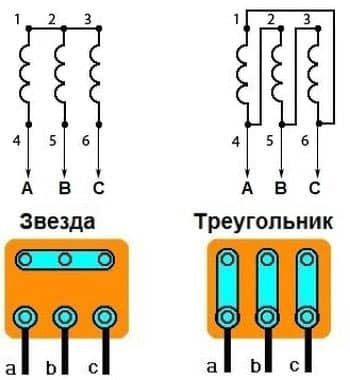
Подключения двигателей могут быть звездой, треугольником, а также всевозможные их переключения. Каждое соединение обладает своими преимуществами и недостатками.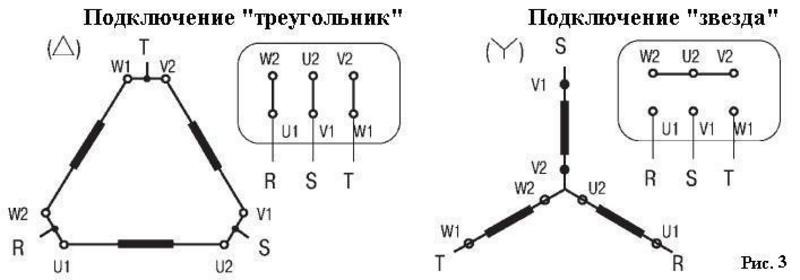
Объединение в одной общей точке: подключение звезда
Концы обмоток статора соединены вместе в одном пункте. Трехфазное напряжение поступает на начало обмоток. Значение пусковых токов при соединении треугольник более мощное. Соединение звезда означает сводку концов обмотки статора. Напряжение поступает на начала каждой обмотки.
Обмотки соединяются последовательно замкнутой ячейкой, образуют треугольное соединение. Ряды контактов с клеммами расположены параллельно по отношению друг к другу. Например, начало вывода 1 находится напротив конца 1. Питание сети подаётся на статорные обмотки, создавая вращения магнитного поля, приводящее к движению ротора. Крутящийся момент, возникающий после подключения трехфазного электродвигателя, является недостаточным для пуска.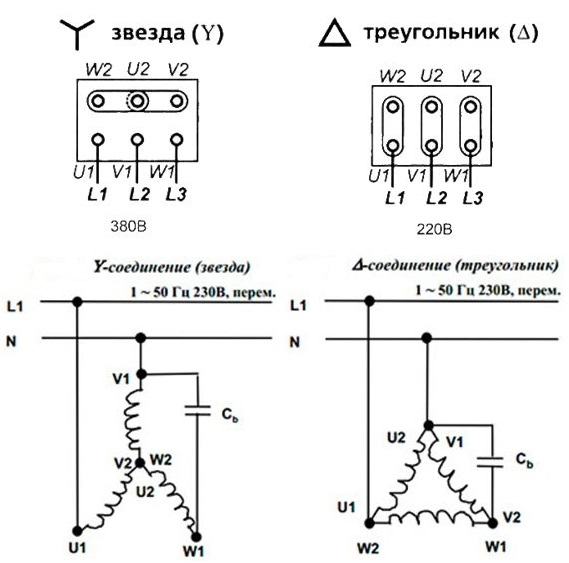
Чертеж подсоединения классического частотного преобразователя звездой
По данной схеме подсоединяются отечественные моторы 380 вольт.
Смешанный способ
Комбинированный тип подключения применим для электромоторов мощностью от 5 кВт. Схема звезда — треугольник используется при необходимости снизить пусковые токи агрегата. Принцип действия начинается со звезды, а после набора двигателем нужных оборотов, происходит автоматическое переключение на треугольник.
Схема пуска трёхфазного электродвигателя с помощью реле

Принцип работы
Пуск питания происходит с помощью второго и релейного контакта. Затем на статоре срабатывает третий пускатель, тем самым размыкая цепь, образованную катушкой третьего элемента, в нем происходит замыкание. Далее первая обмотка статора начинает работать. Затем происходит замыкание в магнитном пускателе, срабатывает временное термореле, которое в третьей точке замыкает. Далее наблюдается замыкание контакта временного термореле в электроцепи второй обмотки статора. После отсоединения обмоток третьего элемента, происходит замыкание контактов в цепочке третьего элемента.
К началу обмоток проходит ток на три фазы. Он поступает через силовые контакты магнита первого элемента. Контакты третьего пускателя включают его, замыкают концы обмоток, которые соединяются звездой.
Затем включается реле времени первого пускателя, третий выключается, а второй включается.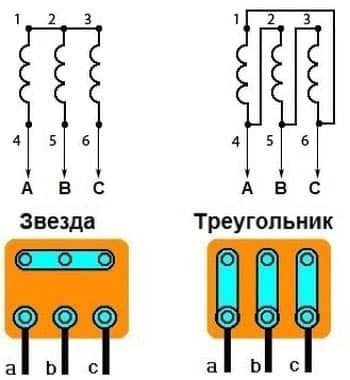 Контакты К2 замыкают, напряжение поступает на концы обмоток. Это и есть включение треугольником.
Контакты К2 замыкают, напряжение поступает на концы обмоток. Это и есть включение треугольником.
Различные производители изготавливают реле пуска, необходимое для запуска электродвигателя. Они отличаются внешне, по названию, но выполняют одинаковую функцию.
Обычно подключение к сети 220 происходит фазосдвигающим конденсатором. Питание поступает от любой электросети, вращает ротор с одинаковой частотой. Конечно, мощность от трёхфазной сети будет больше, чем от однофазной. Если трёхфазный двигатель работает от однофазной сети, теряется мощность.
Некоторые виды моторов не предназначены для работы от бытовой сети. Поэтому выбирая прибор для дома, предпочтение следует отдать двигателям с короткозамкнутыми роторами.
По номинальному питанию отечественные электродвигатели делятся на два типа: мощностью 220 — 127 вольт и 380 — 220 вольт. Первый тип электромоторов небольшой мощности применяется нечасто. Вторые устройства имеют широкое распространение.
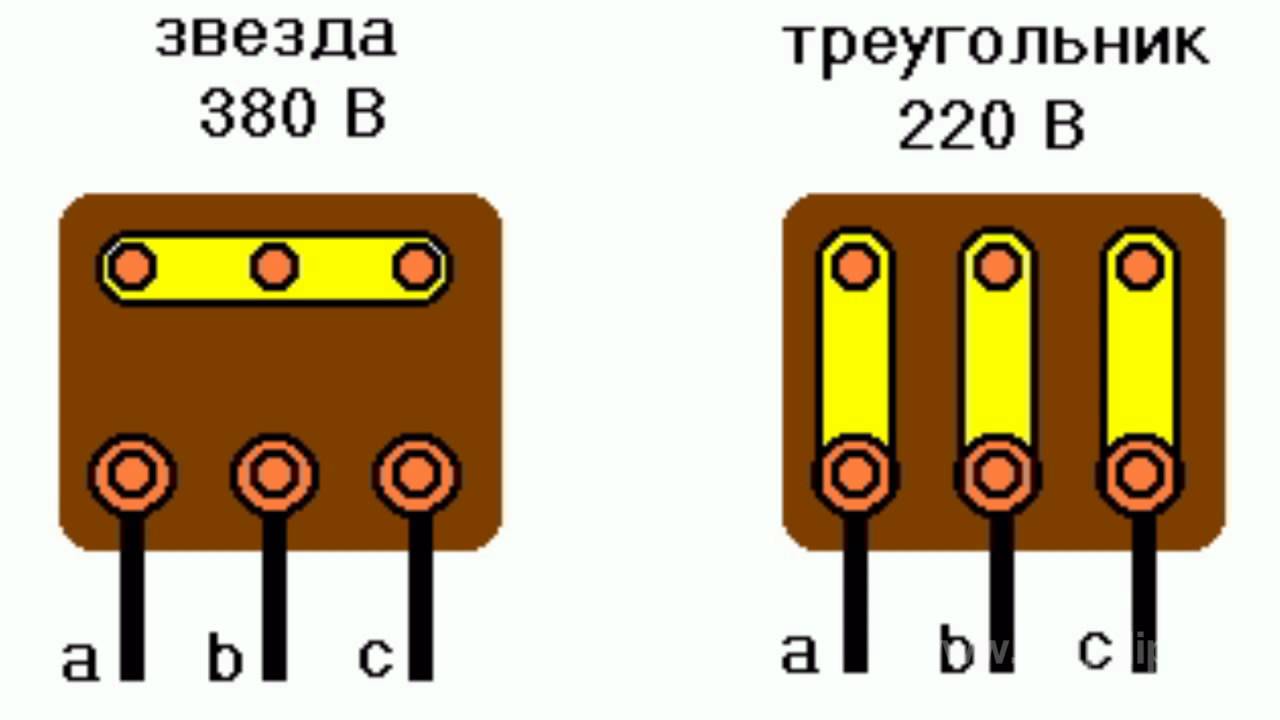
При монтаже электродвигателя любой мощности действует определенный принцип: устройства с низкой мощностью подключается по схеме треугольник, а с высокой соединяются звездой.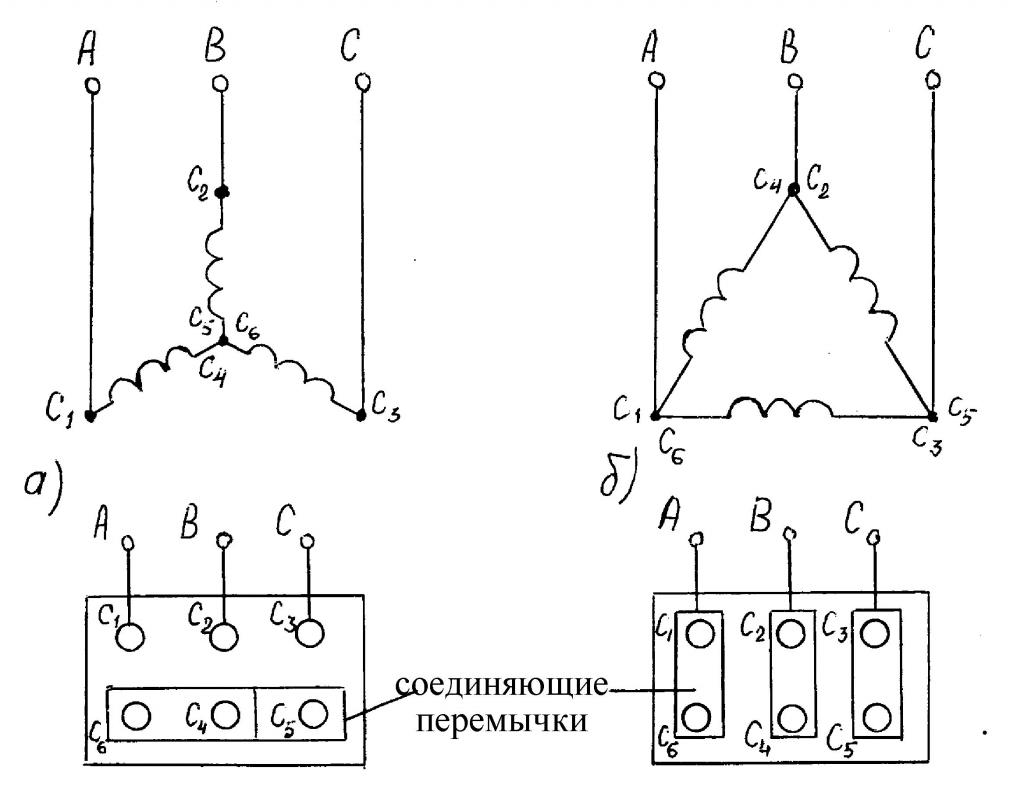 Электропитание 220 поступает на сводку треугольником, напряжение 380 идёт на соединение звездой. Это обеспечит долгую и качественную работу механизма.
Электропитание 220 поступает на сводку треугольником, напряжение 380 идёт на соединение звездой. Это обеспечит долгую и качественную работу механизма.
Рекомендованная схема для подключения двигателя значится в техническом документе. Значок △ означает соединение в этой же форме. Буква Y указывает на рекомендуемую схему подключения звездой. Характеристики многочисленных элементов обозначены цветами, в связи с их маленькими габаритами. По цвету читается, например, номинал, сопротивление. Если стоят оба знака, то соединение возможно переключением △ и Y. Когда стоит одна определенная маркировка, например, Y, то доступное подключение будет только по схеме звезда.
Схема △ даёт мощность на выходе до 70 процентов, значение пусковых токов доходит до максимальной величины. А это может испортить двигатель. Данная схема является единственным вариантом для работы от российских электросетей зарубежных асинхронных двигателей с мощностью 400 — 690 вольт.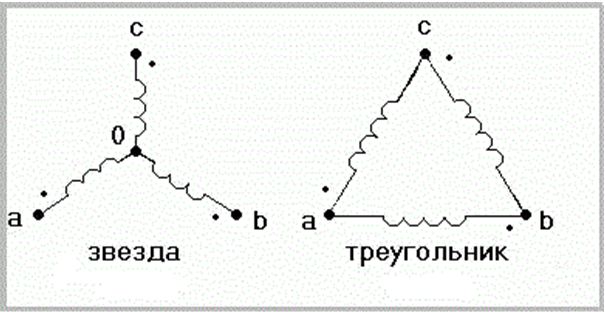
Поэтому выбирать правильное соединение или переключение, необходимо учитывая особенности электрической сети, силовой мощности электродвигателя. В каждом случае следует ознакомиться с техническими характеристиками мотора и оборудования, для которого он предназначен.
Группы соединения трансформаторов
Дата публикации: .
Категория: Электротехника.
Условия параллельной работы трансформаторов.
Большинство трансформаторов питает потребителей параллельными группами. Для включения на параллельную работу трансформаторы должны иметь:
одинаковые коэффициенты трансформации. В противном случае между их вторичными обмотками будет циркулировать уравнительный ток, который даже при небольшой разнице в коэффициентах трансформации может привести к опасному перегреву;
одинаковые напряжения короткого замыкания uк, %, иначе они не смогут делить нагрузку пропорционально своим мощностям 1.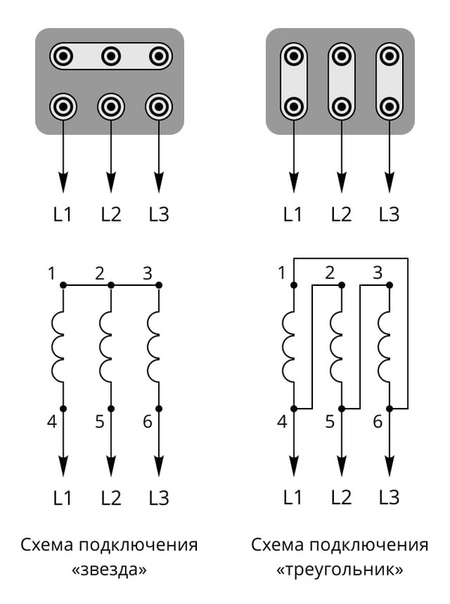 Иными словами, одни трансформаторы будут недогружены, другие – перегружены;
Иными словами, одни трансформаторы будут недогружены, другие – перегружены;
одинаковые группы соединения. Если группы соединения различны, то между соответствующими векторами вторичных напряжений трансформаторов, включаемых параллельно, образуется сдвиг фаз. Он повлечет за собой разность напряжений. А так как в одной и той же точке одновременно не могут существовать разные напряжения, то для их выравнивания между трансформаторами возникнет уравнительный ток. Как объяснено ниже, при самом малом из возможных сдвигов (при разных группах соединения) – сдвиге в 30° – уравнительный ток примерно в 5 раз превышает номинальный ток трансформатора. При самом большом сдвиге – в 180° – в 20 раз.
Что такое группа соединения?
На рисунке 1 изображены 10 трансформаторов, обмотки которых соединены по-разному, причем это далеко не все из возможных соединений. Не рассматривая пока, в чем состоят различия, обратим внимание на помещенные рядом со схемами векторные диаграммы, которые расположены в следующем порядке: слева – векторная диаграмма напряжений первичной обмотки, в середине – векторная диаграмма напряжений вторичной обмотки, справа – векторные диаграммы напряжений обеих обмоток совмещены (в часах).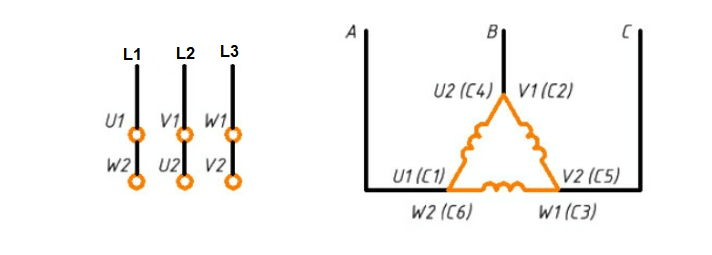 Их «центры тяжести» находятся в центре циферблата часов. Минутная стрелка часов совпадает с направлением одного из векторов напряжений первичной обмотки (на рисунке 1 с вектором B). Часовая стрелка совпадает с вектором напряжения вторичной обмотки одноименной фазы, то есть с вектором b.
Их «центры тяжести» находятся в центре циферблата часов. Минутная стрелка часов совпадает с направлением одного из векторов напряжений первичной обмотки (на рисунке 1 с вектором B). Часовая стрелка совпадает с вектором напряжения вторичной обмотки одноименной фазы, то есть с вектором b.
Рисунок 1. Примеры образования групп соединений трансформаторов.
Начала первичных обмоток обозначены A, B, C, концы X, Y, Z. Начала вторичных обмоток a, b, c концы x, y, z.
Обратите внимание на то, что сравнивается расположение векторов первичной и вторичной звезд. Поэтому в случае соединения обмотки в треугольник надо, перед тем как определять группу соединения, вписать в треугольник звезду. После этого, рассматривая звезды, стрелки направляют вдоль векторов звезд в вершины B и b (A и a, C и c).
По рисунку 1 легко убедиться в том, что несколько схем, несмотря на различие в соединениях, дают одинаковый сдвиг векторов одноименных напряжений, что отчетливо видно по соответствующим им «часам», так как они указывают одно и то же время.
Несколько схем, дающих одинаковый сдвиг, образуют группу соединения. Иными словами, вторичные напряжения одноименных фаз всех трансформаторов, имеющих одну и ту же группу соединения, совпадают по фазе. Поэтому их можно соединять параллельно, не рискуя получить уравнительный ток.
Основных групп может быть двенадцать (1 ч, 2 ч, …, 12 ч) – по числу цифр на циферблате. Это объясняется тем, что векторы первичных и вторичных напряжений в зависимости от схемы соединения обмоток и их расположения на стержнях могут иметь сдвиги, кратные 30°. Таким образом, группе 1 ч соответствует сдвиг 30°, группе 2 ч – 60°, 3 ч – 90°, 4 ч – 120° и так далее. Сдвиг в 360° (или, что то же, отсутствие сдвига, так как 360° и 0° – это одно и то же) имеет группа 12 или 0 ч. При сдвиге 6 ч векторы напряжений одноименных фаз первичных и вторичных обмоток направлены прямо противоположно.
При сдвиге 6 ч векторы напряжений одноименных фаз первичных и вторичных обмоток направлены прямо противоположно.
Четные группы (2, 4, 6, 8, 10, 12) получаются, если обе обмотки высшего напряжения (ВН) и низшего напряжения (НН) имеют одинаковые соединения – обе в звезду или обе в треугольник. Соединение одной обмотки в зигзаг – звезду при другой обмотке, соединенной в треугольник, дает четные группы.
Нечетные группы (1, 3, 5, 7, 9, 11) получаются, если одна обмотка соединена в звезду, другая – в треугольник, а также, если одна обмотка соединена в зигзаг – звезду, а другая – в звезду.
Обозначение группы соединений
состоит из двух частей: слева от черточки расположены знаки или буквы, характеризующие схему соединения обмоток, а справа – цифры, указывающие сдвиг в часовом обозначении.
Схемы соединений обозначают знаками и буквами. Приведем примеры буквенного обозначения: Y или У – звезда, Yн или Y0 или Ун или У0– звезда с выведенной нулевой точкой; Δ или Д или D – треугольник; Z – зигзаг, Zн или Z0 – зигзаг с выведенной нулевой точкой.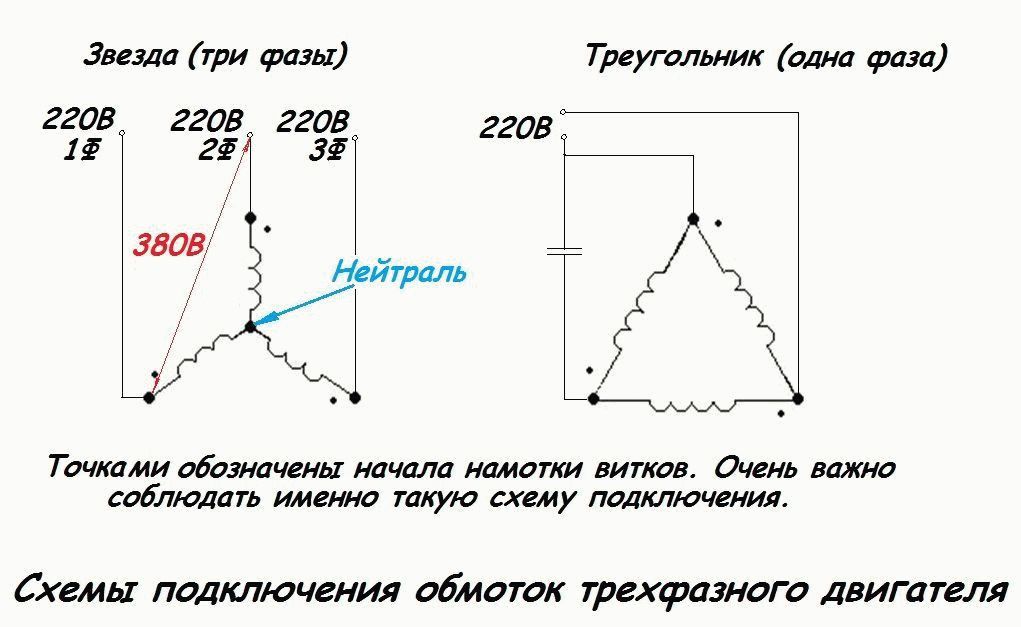
Рассмотрим один пример возможных обозначений группы соединения двухобмоточного трансформатора, у которого обмотка ВН соединена в треугольник, обмотка НН – в звезду с выведенной нулевой точкой и со сдвигом 11 ч (330°, так как 11 × 30° = 330°) между векторами первичного и вторичного напряжений одноименных фаз:
Δ / Yн — 11 или Д / Ун — 11 или Д / У0 — 11 или D / Yн — 11 или D / Y0 — 11.
Из приведенного примера легко понять систему построения обозначений групп соединения двухобмоточных трансформаторов. В левой части числитель дроби указывает схему соединения обмоток высшего напряжения, знаменатель – низшего напряжения. Цифры в правой части – это часовое обозначение группы соединений.
Трехобмоточные трансформаторы обозначаются, например, Ун / У / Д — 12 — 11 или Ун / У / Д — 0 — 11. Это значит, что обмотка ВН соединена в звезду с выведенной нулевой точкой. Обмотка среднего напряжения (СН) соединена в звезду. Соединение обмотки НН – треугольник. Первое число 12 или 0 указывает сдвиг в часовом обозначении между обмотками ВН и СН; второе число 11 – сдвиг между обмотками ВН и НН. Легко понять, что в данном примере сдвиг между СН и НН можно обозначить 11.
Количество групп соединений трансформаторов ограничено стандартами. Но в практике можно столкнуться со всеми 12 группами и даже с такими соединениями, когда направления вращения векторов ВН и НН не совпадают. Такие трансформаторы не имеют группы в часовом обозначении.
Ошибочно получить не ту группу, которая требуется, можно по многим причинам, например вследствие простой перемаркировки фаз, перекрещивания фаз и тому подобного. Поэтому всегда необходима проверка группы соединения, а это ответственная и сложная работа. У трансформаторов, как правило, имеется шесть (семь) выводов на крышке, а не двенадцать, то есть обмотки между собой соединены внутри трансформатора. В этих сложных условиях проверка группы соединения выполняется последовательными измерениями по определенной системе, которая достаточно полно описана в книге Алексенко Г.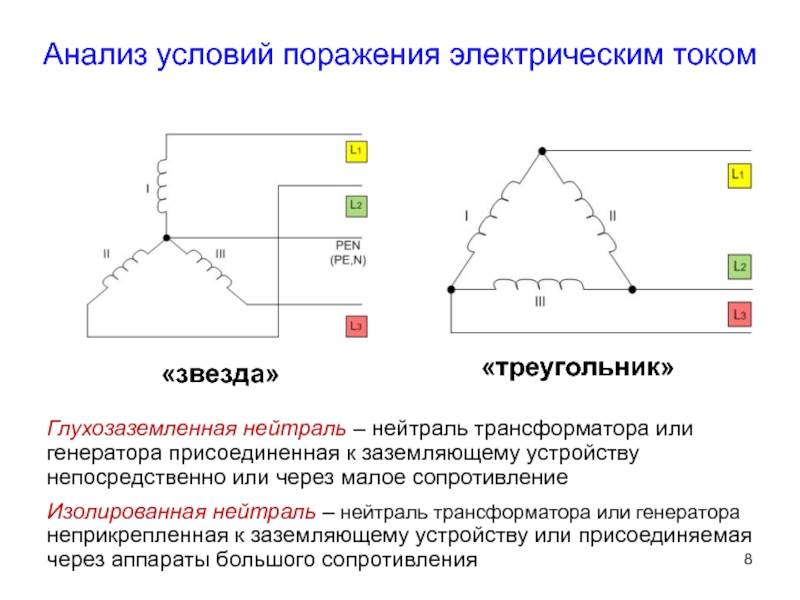 В. «Параллельная работа трансформаторов и автотрансформаторов», 1967г.
В. «Параллельная работа трансформаторов и автотрансформаторов», 1967г.
Пересоединениями на крышке трансформатора можно перевести группы одну в другую: либо группы 12, 4 и 8, либо 6, 10 и 2, либо все нечетные группы.
Приведенные здесь сведения имеют ограниченную цель – показать широкие возможности изменять группу соединения без вскрытия трансформатора. Техника пересоединений с подробными пояснениями для всех практически вероятных случаев подробно описана в вышеуказанной книге.
Техника построения векторных диаграмм, применяющаяся для определения группы соединения.
На схемах обмотки чередуют в таком порядке, как они присоединены к выводам трансформатора. Это значит, что, начиная счет с вывода A обмотки ВН и обходя трансформатор в направлении стрелки (рисунок 2, а), будем встречать его выводы в следующем порядке: A, B, C, c, b, a. Именно так их располагают и на схеме.
Начала обмоток ВН обозначают буквами A, B, C; начала обмоток НН – a, b, c. Концы обмоток ВН обозначают X, Y, Z, концы обмоток НН – x, y, z. Условимся располагать у одинаково намотанных обмоток на схемах все начала вверху, все концы внизу (рисунок 2, б). У обмоток различного направления начала будем располагать с разных сторон (рисунок 2, в).
Концы обмоток ВН обозначают X, Y, Z, концы обмоток НН – x, y, z. Условимся располагать у одинаково намотанных обмоток на схемах все начала вверху, все концы внизу (рисунок 2, б). У обмоток различного направления начала будем располагать с разных сторон (рисунок 2, в).
Рисунок 2. Система обозначений обмоток для определения группы соединений.
Векторы напряжений, относящиеся к одной и той же фазе (обмотки надеты на один стержень), параллельны. Принято строить векторные диаграммы для того момента, когда потенциалы A, a (B, b, C, c) выше потенциалов X, x (Y, y, Z, z).
Наименования фаз первичной обмотки и расположение их векторов напряжения определяются первичной сетью и потому для всех схем соединений одинаковы.
Рассмотрим несколько примеров.
1. Требуется определить группу соединений для схемы на рисунке 3, а. Первый шаг: строим векторную диаграмму обмотки ВН (рисунок 3, б). Второй шаг: строим векторную диаграмму обмотки НН (рисунок 3, в). Следуя ранее оговоренным условиям, векторы AX, BY, CZ и ax, by, cz соответственно параллельны и направлены в те же стороны, так как электродвижущие силы (э. д. с.) обмоток имеют одинаковые направления (их начала обозначены на рисунке 3, а сверху).
Требуется определить группу соединений для схемы на рисунке 3, а. Первый шаг: строим векторную диаграмму обмотки ВН (рисунок 3, б). Второй шаг: строим векторную диаграмму обмотки НН (рисунок 3, в). Следуя ранее оговоренным условиям, векторы AX, BY, CZ и ax, by, cz соответственно параллельны и направлены в те же стороны, так как электродвижущие силы (э. д. с.) обмоток имеют одинаковые направления (их начала обозначены на рисунке 3, а сверху).
Рисунок 3. Примеры определения группы соединения при включении обеих обмоток в звезду.
Третий шаг: совмещаем центр тяжести векторной диаграммы обмотки ВН с центром часов, направляя вектор одной из фаз, например фазы BY, на 12 ч. Четвертый шаг: совмещаем центр тяжести векторной диаграммы НН с центром часов и смотрим, на который час указывает вектор той же фазы, в нашем случае by.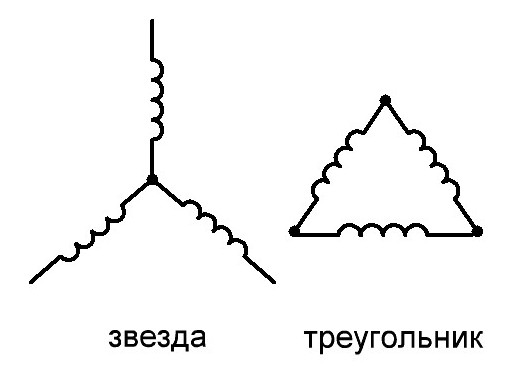 Этот час и определяет собой группу соединения, в данном примере 0 или 12 (рисунок 3, г).
Этот час и определяет собой группу соединения, в данном примере 0 или 12 (рисунок 3, г).
2. Определение группы соединения для схемы на рисунке 3, д, у которой направление обмоток различно, выполнено по тому же плану и пояснений не требует. В данном случае получается группа У / У — 6.
3. Построим векторные диаграммы для схемы на рисунке 4, а с одинаково намотанными обмотками, если обмотка НН соединена в треугольник. Векторная диаграмма обмотки ВН (рисунок 4, б) имеет такой же вид, как на рисунке 3, б. Почему? Потому что она также определяется первичной сетью. Параллельно вектору BY строим вектор by, направляя его в ту же сторону (рисунок 3, в). Затем, видя по схеме, что вывод b соединен с выводом z, ставим на векторной диаграмме рядом с буквой b букву z. А так как точка z принадлежит вектору cz, проводим через нее линию I – I параллельно вектору CZ.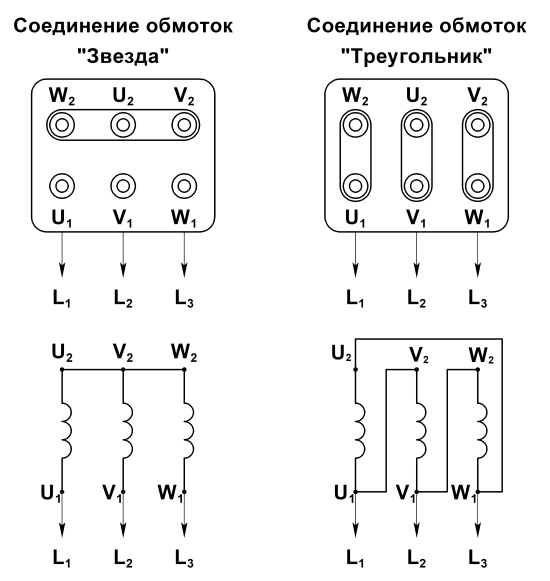 Затем, видя, что вывод y соединен с выводом a, ставим на векторной диаграмме рядом с буквой y букву a и проводим через нее линию II – II, параллельную вектору AX. Точка пересечения линий I – I и II – II образует вершину треугольника, соответствующую соединению между выводами c и x. Остается расставить стрелки у векторов cz и ax.
Затем, видя, что вывод y соединен с выводом a, ставим на векторной диаграмме рядом с буквой y букву a и проводим через нее линию II – II, параллельную вектору AX. Точка пересечения линий I – I и II – II образует вершину треугольника, соответствующую соединению между выводами c и x. Остается расставить стрелки у векторов cz и ax.
Рисунок 4. Примеры определения группы соединения при включении обмотки НН в треугольник
Теперь нужно совместить центры тяжести векторных диаграмм обмоток ВН и НН, поместить их в центр часов и определить группу соединения. В данном случае трансформатор имеет 11-ю группу, так как вектор b показывает 11 ч. Группу в данном случае определяет вектор b, а не векторы a и c, так как на 12 ч направлен вектор B, а не векторы A и C.
Поясним, как были найдены центры тяжести. Центр тяжести обмотки ВН, соединенной в звезду,– ее нулевая точка. Центр тяжести обмотки НН, соединенной в треугольник, находят следующим построением: каждую сторону треугольника делят пополам и ее середину соединяют с противолежащей вершиной. Пересечение полученных трех линий (медиан) и есть центр тяжести.
На рисунке 4, д обмотки также намотаны одинаково и тоже соединены в звезду и треугольник, но получилась группа не 11 ч, а 1 ч. Это объясняется тем, что выполняя соединения обмоток НН, мы на этот раз обходим их иначе, чем на рисунке 4, а. В первом случае конец обмотки by соединялся с началом обмотки ax, во втором – конец обмотки by соединяется с началом обмотки cz. В результате другого направления обхода треугольник повернулся.
При соединении обмоток НН в треугольник мы ориентировались по веторам обмотки ВН, причем, как уже упоминалось, они изображали напряжения питающей сети. Иными словами, вершины треугольника векторов A, B, C были заданы.
Иными словами, вершины треугольника векторов A, B, C были заданы.
При соединении обмоток ВН в треугольник это условие также необходимо соблюдать, откуда следует, что при любом соединении обмоток ВН – и в звезду (рисунок 5, а), и в треугольник (рисунок 5, б и в) – точки A, B, C на векторных диаграммах располагаются одинаково: это сеть. Однако направление векторов при соединении в треугольник может быть различно. Оно определяется порядком выполнения соединений.
Рисунок 5. Расположение векторов при соединении в треугольник обмоток ВН.
Действительно, на рисунке 5, б соединение выполнено от обмотки B к обмотке C, а от нее к обмотке A, чему и соответствует направление стрелок на векторной диаграмме.
На рисунке 5, в соединение выполнено в другом порядке: от обмотки B к обмотке A и от нее к обмотке C. Поэтому направление стрелок на векторной диаграмме изменилось на обратное.
Поэтому направление стрелок на векторной диаграмме изменилось на обратное.
1 Отношение мощностей параллельно включенных трансформаторов не должно быть больше 1 : 3. В противном случае даже небольшие абсолютные перегрузки параллельно работающих трансформаторов могут оказаться в процентном отношении для малых трансформаторов недопустимо большими.
Источник: Каминский Е. А., «Звезда, треугольник, зигзаг» – 4-е издание, переработанное – Москва: Энергия, 1977 – 104с.
Соединение обмоток электродвигателя «треугольником» и «звездой»
На сегодняшний день асинхронные электродвигатели большой мощности отличаются надежностью работы и высокой производительностью, удобством эксплуатации и обслуживания, а также приемлемой ценой. Конструкция этого типа двигателя позволяет выдерживать сильные механические перегрузки.
Как известно, из основ электротехники, основными частями любого двигателя являются статичный статор, и вращающейся внутри его ротор.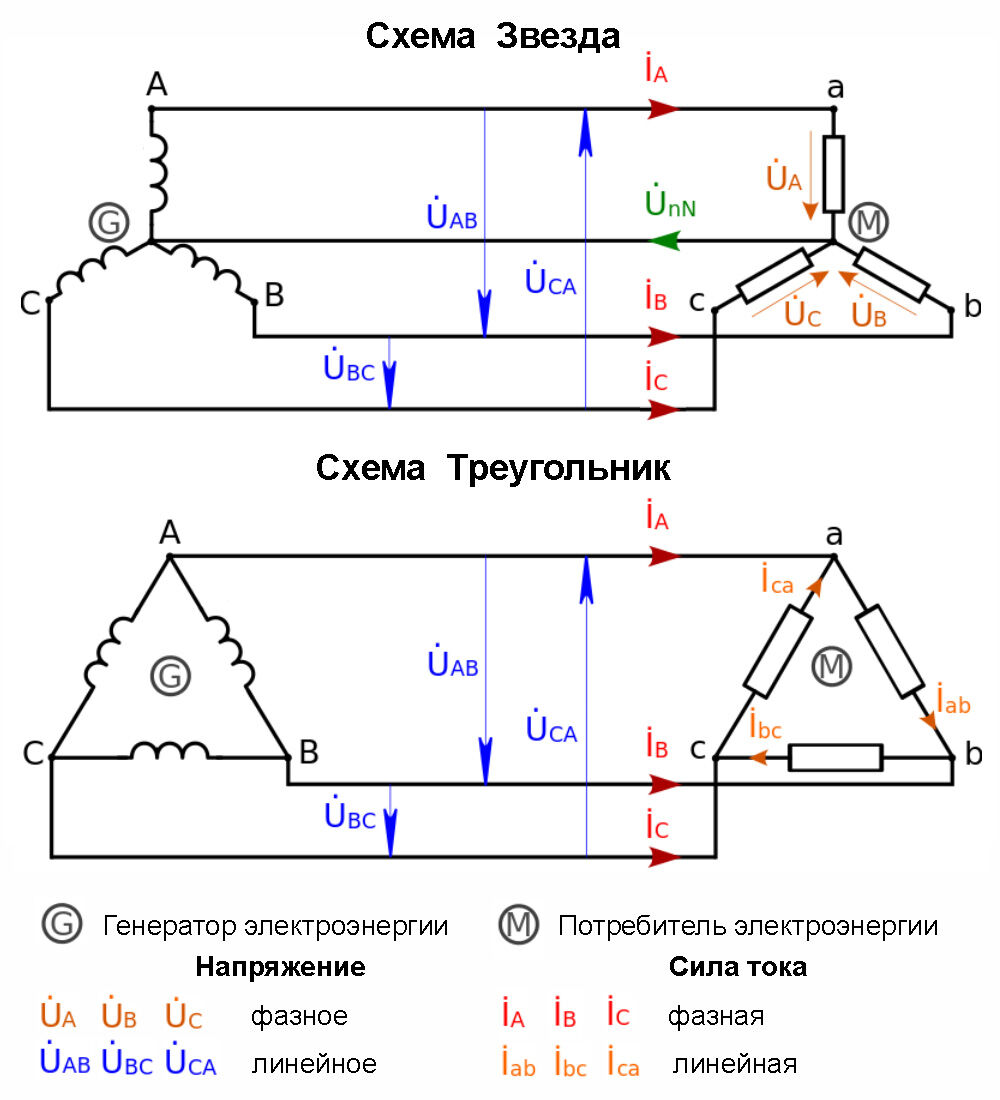
Оба эти элемента состоят из токопроводящих обмоток, при этом статорная обмотка находиться в пазах магнитопровода с соблюдением расстояния в 120 градусов. Начало и конец каждой обмотки выведены в электрическую распределительную коробку и установлены в два ряда.
При подаче напряжения от трехфазной электросети на обмотки статора создается магнитное поле. Именно оно заставляет ротор вращаться.
Как подключить электродвигатель правильно – знает опытный электрик.
Подключение асинхронного двигателя к электрической сети осуществляется только по следующим схемам: «звезда», «треугольник» и их комбинации.
Определение типа способа соединения
Выбор того или иного подсоединения зависит от:
- надежности энергосети;
- номинальной мощности;
- технических характеристик самого двигателя.
Каждое соединение имеет свои плюсы и минусы в работе. В паспорте двигателя от завода-изготовителя, а также на металлическом лейбле на самом устройстве обязательно указана схема его подключения.
При соединении «Звезда» все концы статорных обмоток сходятся водной точке, а напряжение поступает на начало каждой из них. Подключение двигателя «звездой» гарантирует плавный, безопасный пуск агрегата, но на начальном этапе наблюдается значительная потеря нагрузки.
Подключение «треугольником» подразумевает последовательное соединение обмоток в замкнутую структуру, т.е.начало первой фазы соединяют с концом второй и. т.д.
Такое соединение дает выходную мощность до 70% от номинальной, но в таком случае существенно возрастают пусковые токи, что может спровоцировать поломку электродвигателя.
Существует также комбинированное соединение «звезда-треугольник» (такой значок Y/Δ обязательно должен значиться на корпусе мотора). Представленная схема вызывает скачки тока в момент переключения, которые приводят к тому, что скорость вращения ротора быстро снижается, а потом постепенно входит в норму.
Комбинированные схемы актуальны для электромоторов мощностью свыше 5 кВт.
Зависимость выбора от напряжения
Сейчас в промышленности более применимы асинхронные трехфазные электродвигатели отечественного производства, рассчитанные на номинальное напряжение от сети220/380 В. (агрегаты на 127/220 В уже редко используются).
Схема подключения «треугольник»- единственно верная для подключения к российским энергосетям зарубежных электромоторов номинальным напряжением 400-690 В.
Подключение трехфазного двигателя любой мощности осуществляется по определенному правилу: агрегаты низкой мощности присоединяются по схеме «треугольник», а высокомощные – только «звездой».
Так электромотор прослужит долго и проработает без сбоев.
Способ «звезды» применяется при подключении трехфазных асинхронных двигателей номинальным напряжением 127/220 В к однофазным сетям.
Как снизить пусковые токи электродвигателя?
Явление значительного повышения пусковых токов при запуске высокомощных устройств, подсоединенных по схеме Δ, приводит в сетях с перегрузкой к кратковременному падению напряжения ниже допустимого значения. Все это объясняется особой конструкцией асинхронного электродвигателя, у которого ротор с большой массой обладает высокой инерционностью. Поэтому на начальном этапе работы мотор перегружается, особенно это актуально для роторов центробежных насосов, турбинных компрессоров, вентиляторов, станочного оборудования.
Все это объясняется особой конструкцией асинхронного электродвигателя, у которого ротор с большой массой обладает высокой инерционностью. Поэтому на начальном этапе работы мотор перегружается, особенно это актуально для роторов центробежных насосов, турбинных компрессоров, вентиляторов, станочного оборудования.
Чтобы снизить влияние всех этих электротехнических процессов, используют подключение электродвигателя «звездой» и «треугольником». Когда двигатель набирает обороты, ножи специального переключателя (пускателя с несколькими трехфазными контакторами) переводит обмотки статора со схемы Y на Δ.
Для реализации смены режимов кроме пускателя нужно специальное реле времени, благодаря которому происходит временная задержка 50-100 мс при переключении и защита от трехфазного короткого замыкания.
Сама процедура использования комбинированной схемы Y/ Δ эффективно помогает уменьшить пусковые токи мощных трехфазных агрегатов. Происходит это следующим образом:
При подаче напряжения 660 В по схеме «треугольник», каждая обмотка статора получает 380 В (√3 раза меньше), а, следовательно, по закону Ома, в 3 раза уменьшается сила тока. Поэтому при запуске в свою очередь в 3 раза снижается мощность.
Поэтому при запуске в свою очередь в 3 раза снижается мощность.
Но такие переключения возможны только для моторов с номинальным напряжением 660/380 В при включении их в сеть с такими же значениями напряжения.
Опасно подключать электродвигатель с номинальным напряжением 380/220 В в сеть 660/380 В, его обмотки могут быстро перегореть.
И также помните, что вышеописанные переключения недопустимо применять для электромоторов, у которых на валу размещена нагрузка без инерции, к примеру, вес лебедки или сопротивление поршневого компрессора.
Для такого оборудования устанавливают специальные трехфазные электрические двигатели с фазным ротором, где реостаты уменьшают значение токов при пуске.
Чтобы изменить направление вращения электромотора, необходимо сменить местами две любые фазы сети при любом типе подключения.
Для этих целей при эксплуатации асинхронного электродвигателя применяют специальные электроаппараты ручного управления, к которым относятся реверсивные рубильники и пакетные переключатели или более модернизированные приборы дистанционного управления — реверсивные электромагнитные пускатели (рубильники).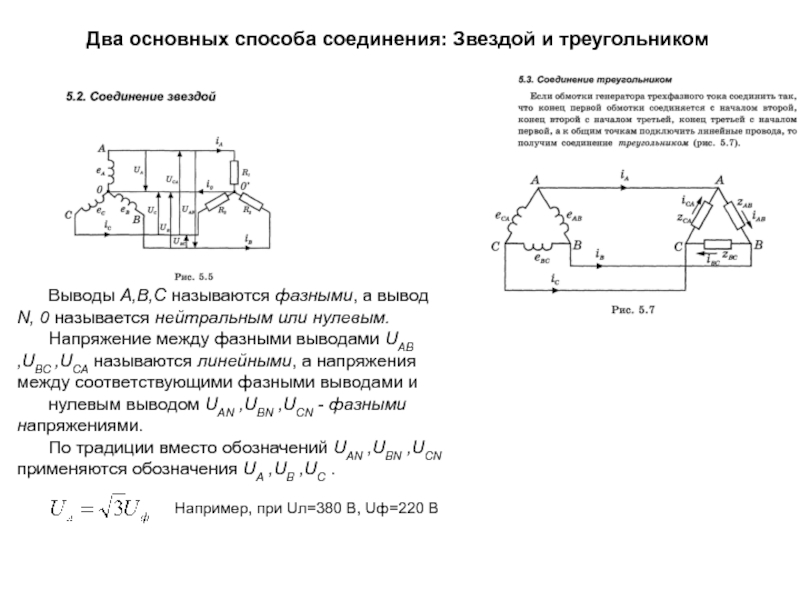 0$ относительно друг друга. В этих обмотках создается трехфазный ток. Напряжения на обмотках равно:
0$ относительно друг друга. В этих обмотках создается трехфазный ток. Напряжения на обмотках равно:
В том случае, если данный генератор использовать без связи друг с другом, то генератор трехфазного тока становится просто совокупностью отдельных генераторов однофазного тока. В том случае, если обмотки соединяются определенным способом, то у трехфазного тока возникают специальные свойства, которые используют в технике. Используют два вида соединений обмоток генератора: «звездой» и «треугольником».
Соединение «звезда»
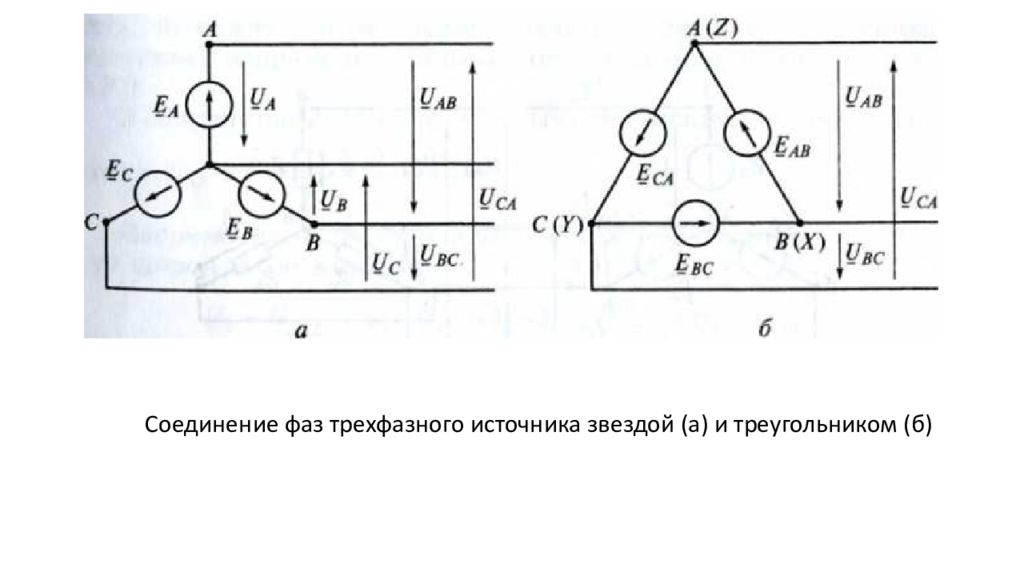
Рассмотрим схему соединения обмоток генератора «звездой». В ней концы трех обмоток соединяют в один узел, а начала служат для подключения нагрузок.
Схема соединения звездой показана на рис.1 (а). Такое соединение обмоток генератора позволяет использовать для передачи электроэнергии вместо шести проводов только четыре. Точка $O$ на схеме — точка общего потенциала (проводник, который соединен с точкой $О$ — нулевой провод). Такое соединение подобно соединению трех источников тока, которое показано на рис.1 (б).
Такое соединение подобно соединению трех источников тока, которое показано на рис.1 (б).
Рисунок 1.
При таком способе соединения напряжение между фазой и нулевым проводом называют фазным напряжением. Напряжение между фазами $A-B$, $B-C$, $C-A$ называют линейным. Для того, чтобы определить как соотносятся фазное и линейное напряжения необходимо брать геометрическую (векторную) разность.
Допустим, что генератор разомкнут, то есть $R_1=\ R_2=R_3=\infty ,\ $найдем связь между фазным напряжением (существующим в каждой из обмоток $О_1,\ О_2,О_3$) и линейными напряжениями (между проводами $0,1,2,3$). Линейное напряжение между проводом $О$ и любым другим проводом равно фазному и его амплитуда $U_m.\ $Линейное напряжение между любой парой проводов $1,2$ и $3$ будет отличаться. Найдем напряжение между проводами $1$ и $3$, которое равно разности потенциалов между свободными концами обмоток $О_1,\ О_2$:
Из формулы (2) видно, что линейное напряжение имеет такую же частоту, что и фазное. \circ \right)\ }$=-${sin \left(\omega t\right)\ }.$
\circ \right)\ }$=-${sin \left(\omega t\right)\ }.$
Мы получили, что при симметричной нагрузке сила тока в нулевом проводе всегда равна нулю. В таком случае (при симметричной нагрузке!) нулевой провод можно удалить совсем и линия будет работать (однако, надо помнить, что при этом на каждую из пар нагрузок будет действовать линейное напряжение в $\sqrt{3}$ раз больше фазного).
Соединение треугольник
Определение 1
Обмотки трехфазного генератора и трехфазные нагрузки могут соединяться еще одним способом. В этом случае конец первой обмотки соединяется с началом второй, конец второй — с началом третьей, конец третьей с началом первой. При этом узлы соединений служат отводами. Такой способ соединения называют треугольником.
Схема соединения треугольник изображена на рис.2(а). Для основной гармоники при соединении обмоток генератора по схеме треугольник ток замыкания в обмотке равен нулю. Обмотки мощных генераторов обычно по такой схеме не соединяют. Эта схема соответствует соединению источников напряжения, которая изображена на рис. 2 (б).
Эта схема соответствует соединению источников напряжения, которая изображена на рис. 2 (б).
Рисунок 2.
Если бы ток был постоянным, то все обмотки при таком соединении были бы замкнуты накоротко. Но, если мы имеем дело с переменными напряжениями, которые имеют разность фаз, то дело коренным образом изменяется. Результирующее напряжение в треугольнике (см. схему вычисления (4)) равно:
Мы получаем, что если генератор не имеет нагрузки, то в обмотках нет тока. Из рис. 2 очевидно, что линейные напряжения равны фазным напряжениям. При разомкнутом генераторе амплитуда линейных напряжений равна амплитуде напряжения в одной обмотке $U_m.$
В соединении треугольником нет нулевого провода, неравномерность нагрузки существеннее сказывается на работе генератора, чем в случае соединения звездой. Из-за этой особенности соединение треугольник чаще всего применяют в силовых установках, например, трехфазных двигателях, где можно получить близкие по величине нагрузки фаз.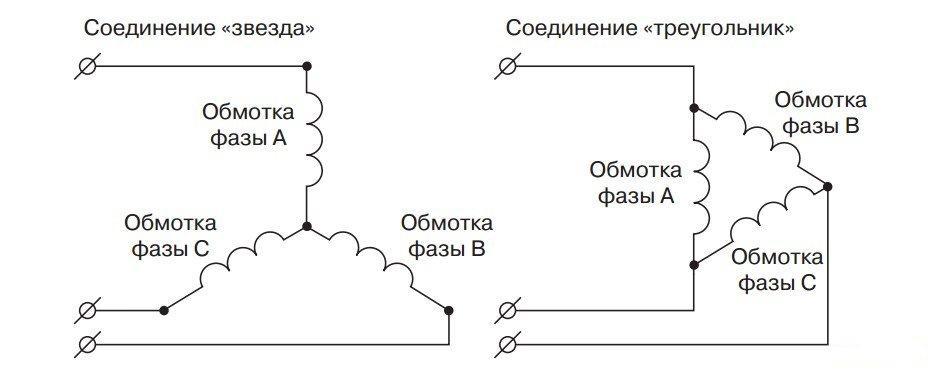
Предполагалось, что генератор и нагрузки соединялись одинаково (звездой или треугольником), конечно, возможны комбинации схем. Например, потребитель соединяется звездой, генератор треугольником.
Пример 1
Задание: Объясните, что произойдет в схеме, которая изображена на рис.1 (а), если оборван провод $1$? Что случится, если перегорел нулевой провод?
Решение:
Допустим, что в схеме соединения звезда (рис.1(а)) оборван провод $1$. Тогда нагрузка $R_1$ , будет выключена. Нагрузки $R_2\ и\ R_3$ будут нормально работать, так как на них будут присутствовать фазные напряжения.
Пусть перегорел нулевой провод. В этом случае каждая пара сопротивлений, например $R_1\ и\ R_2$ будут соединены последовательно и попадут под напряжение в $\sqrt{3}$ раз больше фазного. Это напряжение распределится в соответствии с правилами последовательного соединения, пропорционально сопротивлениям (в данном случае $R_1\ и\ R_2$). Так, если $R_1=R,\ R_2=\frac{1}{10}R$, то на ветке $R_2$ мы получим $0,1U$, а на ветке $R_1$ будет $0,9 U$, где $U$- полное напряжение.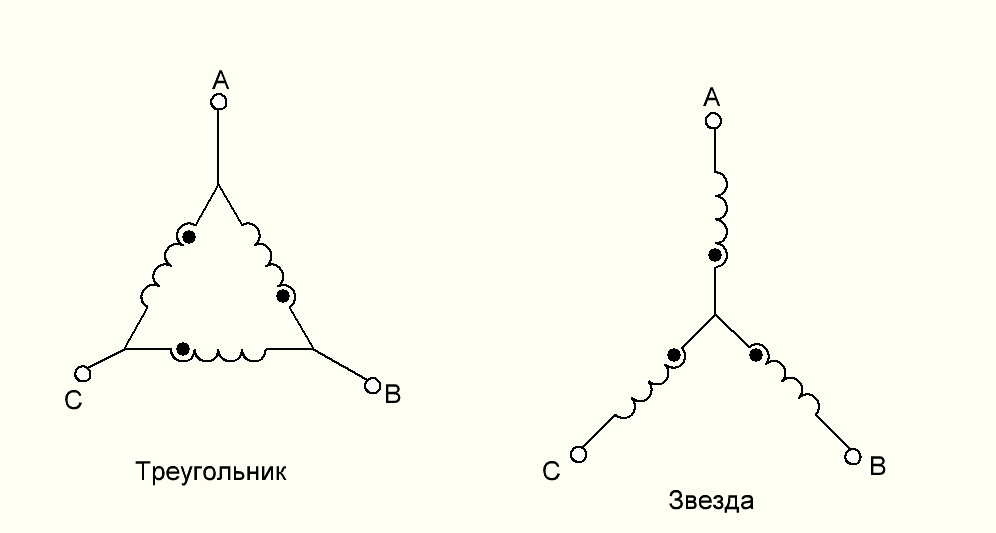 Допустим, что напряжение в сети (фазное) $220В$, тогда:
Допустим, что напряжение в сети (фазное) $220В$, тогда:
Из $380В$ на сопротивление $R_1$ придется $342 В$, тогда как на $R_2$ придется $38В$. Поэтому, если в качестве $R_1$ будет, например бытовая лампочка, она перегорит и ток в обеих ветвях прервётся.
Пример 2
Задание: Объясните, почему соединение звездой применяют в технике освещения?
Решение:
Необходимость применения соединения «звезда», которая имеет нулевой провод, существует в технике освещения, так как при работе осветительных приборов невозможно добиться симметрии в нагрузках. В таких сетях все три фазы и нулевой (нейтральный) провод подводят, например, к жилым домам, внутри дома пытаются примерно одинаково нагрузить каждую фазу, так чтобы общая нагрузка была наиболее симметричной. При этом к каждой квартире приходит нулевой провод и одна из фаз. На распределительный щит, через который проходят две или три фазы, в нулевой провод предохранитель не ставят, так как его перегорание ведет асимметрии напряжений.
Основные сведения о трехфазном токе. Соединение звездой и треугольником
Переменный ток, рассмотренный ранее, называется однофазным. Трехфазным называется ток, представляющий собой совокупность трех однофазных токов, сдвинутых друг относительно друга по фазе.
Простейший генератор трехфазного тока отличается от генератора однофазного тока тем, что имеет три обмотки. При вращении либо этих обмоток в поле постоянного магнита (рис.164), либо самого магнита (рис.165) в обмотках возникают переменные ЭДС одинаковой частоты, сдвинутые друг относительно друга по фазе так, что сумма трех фазных углов составляет .
Если амплитуды ЭДС равны, а сдвиг фаз между двумя любыми смежными ЭДС равен , то трехфазная система называется симметричной. В этом случае на обмотках возникают
одинаковые по величине, но сдвинутые по фазе напряжения: , , .
Использование несвязанных между собой обмоток эквивалентно трем отдельным генераторам и требует для передачи электроэнергии потребителю три пары проводов.
Соединение обмоток между собой позволяет уменьшить количество проводов при передаче энергии и поэтому широко используется в технике.
При соединении обмоток звездой (рис.166) они имеют одну общую точку. Напряжение на каждой обмотке называется фазным. Проводник, соединенный с точкой общего потенциала, называется нулевым проводом. Проводники, соединенные со свободными концами обмоток, называются фазными проводами.
Фазные напряжения, в этом случае, это напряжения между фазными проводами и нулевым проводом. Напряжение между фазными проводами называется линейным. Ток, текущий через обмотки, называется фазным током, а ток текущий в линии, — током линии.
Из векторной диаграммы, при соединении звездой, следует, что . Кроме того при этом фазные токи равны токам в линии.
РИС.166 РИС.167 РИС.168 РИС.169 РИС.170
Если каждую обмотку замкнуть на одинаковую нагрузку R, то суммарная сила тока по нулевому проводу , так как из векторной диаграммы .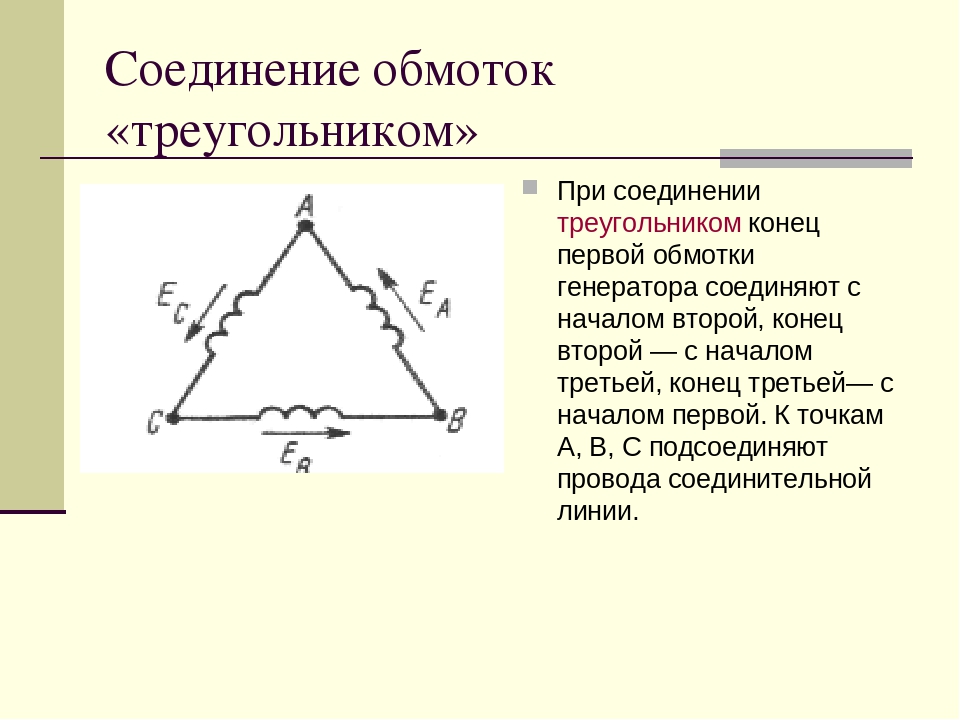
Соединение обмоток генератора звездой позволяет использовать при передаче энергии четыре провода вместо шести.
При соединении обмоток треугольником (рис.168) они образуют замкнутый контур с весьма малым сопротивлением. Линейный провод отходит от общих точек начала одной фазы и конца другой и, поэтому фазные напряжения равны линейным (рис.169).
Из векторной диаграммы токов (рис.170) следует, что
, На практике используется не только соединение обмоток генератора, но и соединение между собой нагрузок звездой или треугольником. Таких комбинаций возможного соединения генератора и нагрузок – четыре.
РИС.171 РИС.172 РИС.173 РИС.174
При соединении звезда – звезда (рис.171) на всех нагрузках разное напряжение, но если сопротивление нагрузок приблизительно равно, то ток по нулевому проводу практически равен нулю.
Тем не менее, нулевой провод нельзя убирать или ставить в него предохранители потому, что без него на каждую из пар нагрузок действует линейное напряжение, причем оно распределяется в соответствии с сопротивлением нагрузок. Получается, что напряжение, подаваемое на нагрузку, зависит от ее сопротивления, что неэффективно и опасно.
Получается, что напряжение, подаваемое на нагрузку, зависит от ее сопротивления, что неэффективно и опасно.
Если генератор и нагрузки соединены звезда – треугольник (рис.172), то на каждой нагрузке, независимо от ее сопротивления, одинаковое напряжение, равное линейному.
При соединении треугольник – треугольник (рис.173) на всех нагрузках фазное напряжение, независимо от их сопротивления.
Если генератор и нагрузки соединены треугольник – звезда (рис.174), то на каждой нагрузке напряжение равно .
Трехфазный ток используется для получения вращающегося магнитного поля. В этом случае трехфазный ток подводится к трем обмоткам, расположенным на неподвижной станине – статоре. Внутри статора помещен стальной барабан – ротор, вдоль образующих которого в пазах уложены провода, соединенные между собой на обоих торцах кольцами.
Обмотки статора создают магнитный поток одинаковой величины, но сдвинутый по фазе, т.е. он как бы вращается относительно ротора. В обмотках ротора возникают индукционные потоки, которые, в свою очередь, взаимодействуют с вращающимся магнитным потоком, что приводит ротор во вращение, т.е. получается электродвигатель достаточно простого устройства.
В обмотках ротора возникают индукционные потоки, которые, в свою очередь, взаимодействуют с вращающимся магнитным потоком, что приводит ротор во вращение, т.е. получается электродвигатель достаточно простого устройства.
При увеличении скорости ротора уменьшается относительная скорость движения его проводников относительно магнитного поля. Если бы он достиг той же скорости вращения, что и магнитный поток статора, то индукционный ток равнялся бы нулю и, соответственно, вращающий момент стал бы равным нулю.
Следовательно, при наличии тормозного момента магнитный поток и ротор не могут вращаться с той же скоростью, что и поток статора (синхронно), — скорость вращения ротора всегда несколько меньше. Поэтому двигатели такого типа называются асихронными (несинхронными).
Трехфазная система, изобретенная русским инженером М.О. Доливо-Добровольским в XIX, применяется во всем мире для передачи и распределения энергии. Доливо-Добровольский первым получил вращающееся магнитное поле с помощью трехфазного тока и построил первый асинхронный двигатель. Трехфазная система обеспечивает наиболее экономичную передачу энергии и позволяет создать надежные в работе и простые по устройству электродвигатели, генераторы и трансформаторы.
Трехфазная система обеспечивает наиболее экономичную передачу энергии и позволяет создать надежные в работе и простые по устройству электродвигатели, генераторы и трансформаторы.
На практике, например, электрические лампы изготавливаются на номинальные напряжения 127 и 220В. Способ их включения в цепь трехфазного тока зависит от величины линейного напряжения трехфазной сети.
Лампы с номинальным напряжением 127 В включаются звездой с нейтральным проводом при линейном напряжении сети 220 В или треугольником при линейном напряжении сети 127 В.
Лампы с номинальным напряжением 220 В соответственно включаются звездой в сеть с линейным напряжением 380 В и треугольником в сеть с напряжением 220 В.
Обмотки трехфазных двигателей изготавливаются на номинальные фазные напряжения 127, 220 и 380 В. Каждый трехфазный двигатель может быть включен или звездой в трехфазную сеть с линейным напряжением, превышающим его фазное в раз, или треугольником, если линейное напряжение сети равно фазному напряжению его обмотки. Обычно на паспорте двигателя указано, например: треугольник -220В, звезда – 380В.
Обычно на паспорте двигателя указано, например: треугольник -220В, звезда – 380В.
Линейные цепи. Правила Кирхгофа. Методы анализа линейных цепей. Переходные процессы в цепи с конденсатором.
Элемент электрической цепи называется линейным, если его параметры не зависят от напряжения и силы тока, т.е. вольт-амперная характеристика прямая.
Электрическая цепь называется линейной если она состоит из линейных элементов.
Применение закона Ома для расчета сложных разветвленных цепей, содержащих несколько источников довольно сложно. Для расчетов таких цепей используют два правила немецкого физика Г. Кирхгофа, первое из которых вытекает из закона сохранения заряда, а второе является обобщением закона Ома на произвольное число источников сторонних ЭДС в изолированном замкнутом контуре.
Для того чтобы использовать правила Кирхгофа необходимо ввести несколько понятий.
Электрическая схема – графическое изображение электрической цепи.
Ветвь электрической цепи – один или несколько последовательно соединенных элементов цепи, по которым течет один и тот же ток.
Узел – соединение трех или большего количества ветвей. Ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:
Например, для узла на рис.64 I1-I2+I3-I4-I5=0
Контур – любой замкнутый путь, проходящий по нескольким ветвям. Положительное направление обхода контура выбирается произвольно, но одно и то же для всех контуров электрической цепи. Токи совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода – отрицательными. ЭДС считаются положительными, если они создают ток, направленный в сторону обхода контура.
Рассмотрим цепь, содержащую три источника (рис.65). Пусть R1, R2, R3 общие сопротивления ветвей АВ, ВС, СА соответственно. Положительное направление обхода примем по часовой стрелке. Применим к каждой ветви закон Ома для неоднородного участка цепи.
Применим к каждой ветви закон Ома для неоднородного участка цепи.
Сложив почленно эти уравнения, получим
Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:
При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:
1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов выяснится при решении: если искомый ток получится положительным, то его направление было выбрано правильно, а если отрицательным, то его истинное направление противоположно выбранному;
2. Выбрать направление обхода контуров и строго его придерживаться; записывая со соответствующими знаками токи и ЭДС;
3. Составить количество уравнений равное количеству искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи).
Площадь треугольников
Есть несколько способов найти площадь треугольника.
Зная базу и высоту
Когда мы знаем основание и высоту, это легко.
Это просто половина b раз h
Площадь = 1 2 bh
(Более подробная информация на странице «Треугольники»)
Самое главное, чтобы основание и высота были под прямым углом. Поиграйте здесь:
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ bh = ½ × 20 × 12 = 120
Знание трех сторон
Существует также формула для определения площади любого треугольника, когда мы знаем длины всех трех его сторон.
Его можно найти на странице формул Герона.
Зная две стороны и угол наклона
Когда мы знаем две стороны и включенный угол (SAS), мы можем использовать другую формулу (фактически, три эквивалентные формулы).
В зависимости от того, какие стороны и углы нам известны, формулу можно записать тремя способами:
Площадь = 1 2 ab sin C
Площадь = 1 2 до н.э. sin A
Площадь = 1 2 ca sin B
Это действительно та же формула, только с измененными сторонами и углом.
Пример: Найдите площадь этого треугольника:
Прежде всего мы должны решить, что мы знаем.
Мы знаем угол C = 25º, а стороны a = 7 и b = 10.
Итак, приступим:
Площадь = (½) ab sin C
Введите известные нам значения: ½ × 7 × 10 × sin (25º)
Сделайте некоторую работу с калькулятором: 35 × 0,4226 …
Площадь = 14,8 с точностью до одного десятичного знака
Как помнить
Подумайте только о «abc»: Площадь = ½ a b sin C
Также хорошо помнить, что угол между двумя известными сторонами всегда равен , что называется «включенным углом».
Как это работает?
Мы знаем, как найти область, когда знаем базу и высоту:
Площадь = ½ × основание × высота
|
В этом треугольнике:
|
Получаем:
Площадь = ½ × (c) × (b × sin A)
Что (проще):
Площадь = 1 2 до н.э. sin A
Изменив метки на треугольнике, мы также можем получить:
- Площадь = ½ ab sin C
- Площадь = ½ ca sin B
Еще один пример:
Пример: Найдите сколько земли
Фермер Джонс владеет треугольным участком земли.
Длина забора АВ составляет 150 м. Длина забора БЦ 231 м.
Угол между ограждением AB и ограждением BC составляет 123º.
Сколько земли принадлежит фермеру Джонсу?
Прежде всего мы должны решить, какие длины и углы нам известны:
- AB = c = 150 м,
- BC = a = 231 м,
- и угол B = 123º
Итак, мы используем:
Площадь = 1 2 ca sin B
Введите известные нам значения: ½ × 150 × 231 × sin (123º) м 2
Сделайте некоторую работу калькулятора: 17,325 × 0.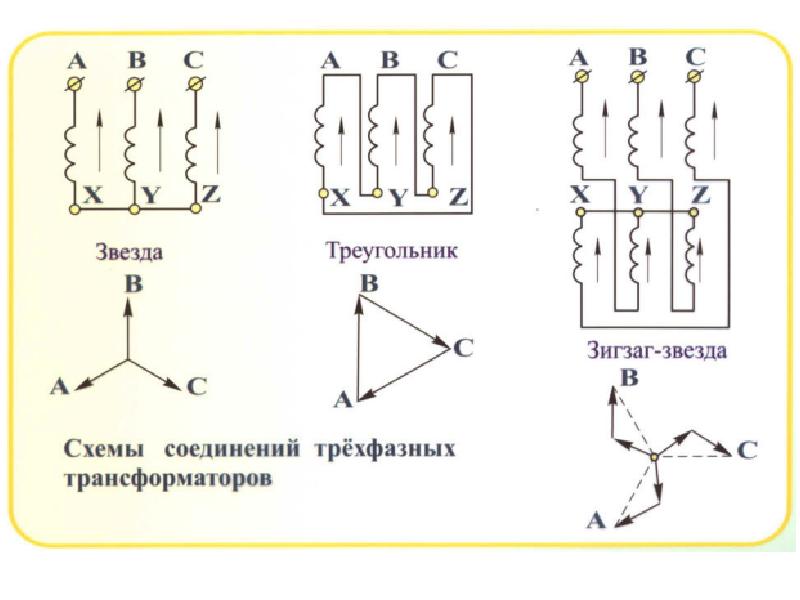 838 … м 2
838 … м 2
Площадь = 14530 м 2
Фермер Джонс владеет 14530 м 2 земли
Решение треугольников SAS
«SAS» означает «Сторона, угол, сторона»
| « SAS » — это когда мы знаем две стороны и угол между ними. |
Чтобы решить треугольник SAS
Пример 1
В этом треугольнике мы знаем:
- угол A = 49 °
- б = 5
- и c = 7
Чтобы решить треугольник, нам нужно найти сторону a и углы B и C .
Используйте закон косинусов, чтобы найти первую сторону a :
a 2 = b 2 + c 2 — 2bc cosA
a 2 = 5 2 + 7 2 — 2 × 5 × 7 × cos (49 °)
a 2 = 25 + 49-70 × cos (49 °)
а 2 = 74 — 70 × 0,6560 . ..
a 2 = 74 — 45,924 … = 28,075 …
а = √28.075 …
а = 5,298 …
a = 5,30 до 2 знаков после запятой
Теперь мы используем Закон синусов, чтобы найти меньший из двух других углов.
Почему угол меньше? Потому что функция обратного синуса дает ответы менее 90 ° даже для углов более 90 °. Выбирая меньший угол (у треугольника не должно быть двух углов больше 90 °), мы избегаем этой проблемы. Примечание: меньший угол — это угол, обращенный к более короткой стороне.
Выберите угол B:
грех B / b = грех A / a
sin B / 5 = sin (49 °) / 5,298 …
Вы заметили, что мы не использовали a = 5,30 . Это число округляется до двух знаков после запятой. Намного лучше использовать неокругленное число 5,298 … которое все еще должно быть на нашем калькуляторе после последнего расчета.
sin B = (sin (49 °) × 5) / 5,298 . ..
..
грех В = 0,7122 …
B = sin −1 (0.7122 …)
B = 45,4 ° с точностью до одного десятичного знака
Теперь мы находим угол C, который легко вычислить, добавив «углы треугольника к 180 °»:
С = 180 ° — 49 ° — 45,4 °
C = 85,6 ° с точностью до одного десятичного знака
Теперь мы полностью решили треугольник, т.е. мы нашли все его углы и стороны.
Пример 2
Это тоже треугольник SAS.
Прежде всего найдем r , используя Закон косинусов:
r 2 = p 2 + q 2 — 2pq cos R
r 2 = 6,9 2 + 2,6 2 — 2 × 6,9 × 2,6 × cos (117 °)
r 2 = 47,61 + 6,76 — 35,88 × cos (117 °)
r 2 = 54,37 — 35,88 × (-0,4539 …)
r 2 = 54,37 + 16,289 ..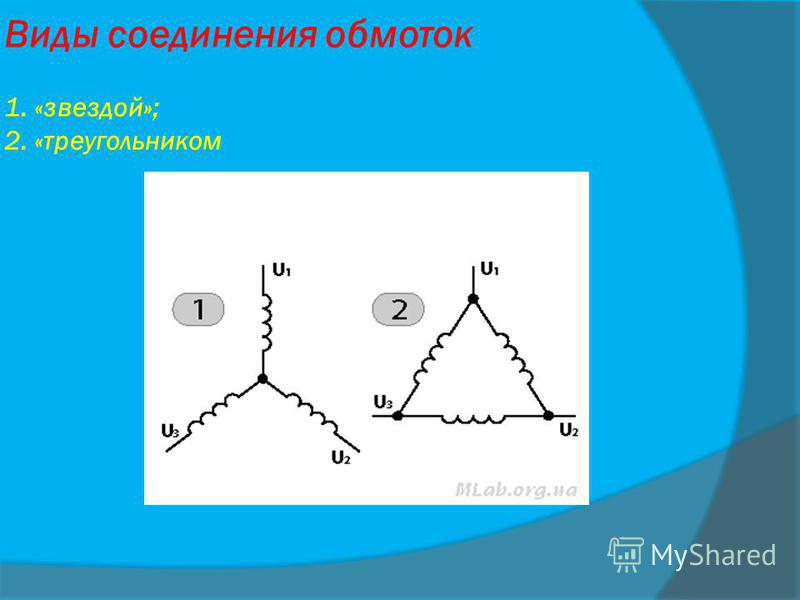 .
= 70,659 …
.
= 70,659 …
r = √70,659…
г = 8,405 … = 8,41 до 2 знаков после запятой
Теперь о законе синуса.
Выбрать меньший угол? Нам не обязательно! Угол R больше 90 °, поэтому углы P и Q должны быть меньше 90 °.
sin P / p = sin R / r
sin P / 6.9 = sin (117 °) / 8,405 …
sin P = (sin (117 °) × 6,9) / 8,405 …
sin P = 0,7313 …
P = sin −1 (0.7313 …)
P = 47,0 ° с точностью до одного десятичного знака
Теперь найдем угол Q, используя «углы треугольника добавить к 180 °»:
Q = 180 ° — 117 ° — 47,0 °
Q = 16,0 ° с точностью до одного десятичного знака
Чтобы овладеть этим навыком, нужно много практики, так что …
В чем разница между равносторонним и равнобедренным треугольниками?
Наука
- Анатомия и физиология
- Астрономия
- Астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
Это просто треугольник или что на самом деле означает символ?
Символ помогает или мешает нам думать о дизайне?
Символы важны, но что, если символ может означать несколько вещей?
Это может привести к проблемам, как мы увидим.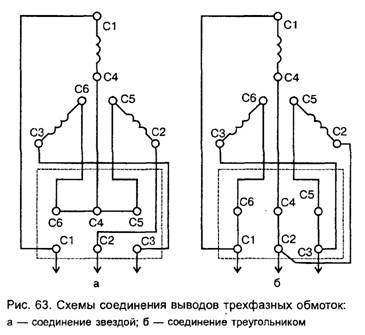 В аналоговом мире треугольник может обозначать операционный усилитель, компаратор или инструментальный усилитель. Вы можете заставить один из них выполнять функцию другого, но производительность системы не будет оптимальной. Давайте посмотрим на их различия и на то, чего следует остерегаться, чтобы мы могли проектировать вокруг них, если это возможно. Как мы увидим, бывают случаи, когда вы даже не хотите пытаться проектировать с неправильным типом детали.
В аналоговом мире треугольник может обозначать операционный усилитель, компаратор или инструментальный усилитель. Вы можете заставить один из них выполнять функцию другого, но производительность системы не будет оптимальной. Давайте посмотрим на их различия и на то, чего следует остерегаться, чтобы мы могли проектировать вокруг них, если это возможно. Как мы увидим, бывают случаи, когда вы даже не хотите пытаться проектировать с неправильным типом детали.
Глядя на рисунок 1, какой треугольник соответствует операционному усилителю? Какой треугольник является компаратором? А в каком треугольнике находится инструментальный усилитель? Ответ:
Они все!
Рисунок 1.Операционный усилитель, входной усилитель и компаратор.Итак, в чем разница и почему нас это волнует? Глядя на таблицу 1, мы видим, что есть некоторые большие различия в некоторых характеристиках, но что они означают на уровне схемы и системы?
| Операционный усилитель | Компаратор | In-Amp | |
| Обратная связь | отрицательное | Нет / положительно | внутренний |
| Усиление разомкнутого контура | От 5 тыс. До 10 миллионов | от 3k до 50k | Фиксированный 0.От 2 до 10 тыс. |
| Коэффициент усиления по замкнутому контуру | Обычно <10,000 | Фиксированный от 0,2 до 10 тыс. | |
| Входные колпачки | Никогда | Может быть | Хорошо |
| Выход | Аналоговый / линейный | Цифровой | Аналоговый / линейный |
| Важные характеристики | V OS , GBW / PM | Задержка пропуска | CMRR |
| Программирование | R или C | Нет | R, SPI, перемычки |
Посмотрим, как можно попасть в беду…
Обратная связь
Операционный усилитель имеет огромное усиление.В инженерной школе нам сказали начинать анализ с разницы между двумя входными данными, равной нулю. Но в реальной жизни это не может быть правдой. Если коэффициент усиления без обратной связи равен 1 миллиону, то для получения 5 В на выходе вам потребуется 5 мкВ на входе. Для пригодной к использованию схемы нам необходимо применить обратную связь, поэтому, когда выход пытается стать слишком высоким, управляющий сигнал возвращается на вход, противодействуя исходному стимулу, например, отрицательной обратной связи. При использовании в качестве компаратора без обратной связи выход будет ударяться по одной шине или другой; при положительной обратной связи он будет двигаться дальше в том же направлении.Итак, операционным усилителям нужна отрицательная обратная связь. Фактически, когда некоторые операционные усилители используются в качестве компараторов без обратной связи, ток питания может быть в 5-10 раз выше максимального значения, указанного в паспорте. 1
Однако для компаратора положительная обратная связь — это именно то, что нам нужно. При отсутствии обратной связи, если один вход компаратора медленно пересекает уровень другого входа, выход начнет медленно изменяться. Если в системе есть шум, такой как отскок от земли, выход может измениться, что, безусловно, нежелательно в системе управления.Но затем он начинает меняться обратно, что приводит к колебательному поведению, иногда называемому дребезжанием (см. Рисунок 5 в MT-083 2 ). Преимущества добавления положительной обратной связи, также называемой гистерезисом, подробно описаны в статье Резы Могими «Устранение нестабильности компаратора с помощью гистерезиса». 3
Рис. 2. Классический входной усилитель с 3 ОУ.Для инструментального усилителя обратная связь уже является внутренней, поэтому добавление обратной связи просто приводит к неточному усилению. Типичный способ создания инструментального усилителя с операционными усилителями показан на рисунке 2.
Примечание: есть обратная связь по каждому отдельному операционному усилителю. Начнем с использования стандартной диаграммы отрицательной обратной связи (см. Рисунок 3) с входным усилителем G, с желаемым усилением 10, что подразумевает коэффициент обратной связи 0,1. Затем выберите фиксированное усиление входного усилителя, равное 100. Используя уравнение 1, фактическое усиление замкнутого контура будет 9,09, почти 10% ошибка. Таким образом, использование треугольника в усилителе в качестве операционного усилителя и создание обратной связи не имеет смысла.
Рисунок 3. Классическая схема обратной связи.Для ОУ нам очень нужна отрицательная обратная связь; для компаратора очень нужны положительные отзывы; а для in-amp нам не нужны отзывы.
Усиление разомкнутого и замкнутого контура
Для операционных усилителей, глядя на уравнение 1, чем выше коэффициент усиления без обратной связи (A VOL ), тем точнее будет коэффициент усиления с обратной связью. Большинство операционных усилителей имеют коэффициент усиления в разомкнутом контуре от 100 000 до 10 миллионов, но некоторые из старых высокоскоростных операционных усилителей могут иметь значение всего 3000. Как показано ранее, чем выше коэффициент усиления разомкнутого контура, тем ниже ошибка усиления замкнутого контура. .
Для компаратора, если размах логики на выходе составляет 3 В, и вам нужен порог 1 мВ, то минимальное усиление должно быть 3000.Более высокое усиление даст вам меньшее окно неопределенности, но если усиление слишком велико, микровольтный шум вызовет срабатывание компаратора.
Для инструментального усилителя концепция усиления без обратной связи действительно не применима.
Входные конденсаторы
Конденсаторы часто добавляются в схемы для ограничения пропускной способности. Глядя на рисунок 4, на первый взгляд кажется, что R1 и C1 образуют фильтр нижних частот. Это не работает и может привести к колебаниям. Коэффициент обратной связи для инвертирующего усилителя равен R2 / R1, но на рисунке 4 коэффициент обратной связи равен R2 / (R1 + Xc).По мере увеличения частоты коэффициент обратной связи увеличивается, поэтому коэффициент усиления шума увеличивается до +20 дБ / декаду, в то время как коэффициент усиления разомкнутого контура операционного усилителя снижается до –20 дБ / декаду. Они пересекаются на уровне 40 дБ, что, согласно теории систем управления, гарантирует колебания. Правильный способ ограничить полосу пропускания схемы — подключить конденсатор к R2.
Рисунок 4. Попытка уменьшить полосу пропускания операционного усилителя. Компараторыобычно не имеют цепи отрицательной обратной связи, поэтому простые R и C перед компаратором на рисунке 5, образующие фильтр нижних частот, работают хорошо.R HYS должен быть намного больше, чем R7, и оба делят размах выходного сигнала, чтобы обеспечить небольшую положительную обратную связь (гистерезис). Если компаратор имеет встроенный гистерезис, такой как LTC6752 или ADCMP391, то R7 и R HYS не используются.
Рисунок 5. Компаратор с ФНЧ и гистерезисом.Для инструментальных усилителей ограничение на входах вполне приемлемо, как показано C4 на рисунке 6. Рисунок в главе 5 руководства по инструментам Analog Devices 4 показывает, что нужно делать каждый раз, когда вы используете инструментальный усилитель.Если вы разместите печатную плату с соответствующими дорожками и контактными площадками, чтобы можно было добавить два резистора и три конденсатора, вы можете начать с резисторов 0 Ом и без конденсаторов и измерить производительность системы. Регулируя значения пяти компонентов, вы можете установить спад синфазного и нормального спада независимо (подробности см. В руководстве).
Рисунок 6. Фильтр радиопомех перед инструментальным усилителем.Выходы
Операционный усилитель или инструментальный усилитель будет иметь выход, который переключается от одной шины к другой.В зависимости от того, использует ли выходной каскад конфигурацию с общим эмиттером или с общим источником, он может находиться в пределах от 25 мВ до 200 мВ для любой шины. Это будет считаться выпуском продукции с железнодорожного транспорта. Если операционный усилитель запитан от +15 В и –15 В, это неудобно для взаимодействия с цифровой схемой. Было испробовано одно плохое решение — поставить на выход диодные зажимы, чтобы защитить цифровой вход от повреждений. Вместо этого ток операционного усилителя становится заоблачным, и операционный усилитель выходит из строя. Существуют более сложные способы подключения операционного усилителя к цифровой логике, но зачем беспокоиться? Просто используйте компаратор.
Компараторымогут иметь выход CMOS с тотемным полюсом, NPN или NMOS выход с открытым коллектором или открытым стоком. Хотя выход с открытым коллектором или открытым стоком требует подтягивающего резистора, что приводит к неравному времени нарастания и спада, он дает преимущество работы компаратора на одном напряжении, скажем 5 В, и сопряжения с логикой, работающей на другом. напряжение, например 3,3 В.
Важные характеристики
Для операционного усилителя нам нужна полоса усиления, превышающая наивысшую частоту сигнала, чтобы уменьшить ошибку замкнутого контура.Глядя на уравнение 1, мы можем увидеть, где правило усиления полосы пропускания должно быть от 10 до 100 раз больше максимальной частоты сигнала. Из уравнения 1, как обсуждалось ранее, обратите внимание, что VOL является функцией частоты и влияет на точность замкнутого контура. Запас по фазе также важен и будет меняться в зависимости от емкостной нагрузки, поэтому в таблице характеристик должны быть четко указаны условия испытаний. Для обеспечения точности постоянного тока напряжение смещения должно быть низким. Для биполярного операционного усилителя с усечением хорошо подходит диапазон от 25 мкВ до 100 мкВ; для операционного усилителя с полевым транзистором хорошо подходит диапазон от 200 мкВ до 500 мкВ.Операционные усилители с автоматическим обнулением / прерыванием / дрейфом нуля почти всегда имеют максимум ниже 20 мкВ, и это выше температуры. Для примеров см. Некоторые типовые спецификации операционных усилителей, такие как OP27, AD8610 или ADA4522.
Рисунок 7. Двунаправленное измерение тока с высоким синфазным колебанием.Задержка распространения — ключевая характеристика компараторов. В отличие от операционных усилителей, которые работают медленнее при перегрузке, компараторы будут работать быстрее при перегрузке. В таблицах спецификаций иногда будет задержка распространения с небольшим перегрузом, скажем, 5 мВ, и другая задержка с большим перегрузом, равным 50 мВ или даже 100 мВ.
Спецификация номер один для инструментальных усилителей — коэффициент подавления синфазного сигнала (CMRR). Вы пытаетесь извлечь очень малый дифференциальный сигнал поверх большого синфазного напряжения. Как и во многих спецификациях, это зависит от частоты, и иногда указывается CMRR постоянного тока или CMRR на очень низкой частоте. Обычно предоставляется график зависимости CMRR от частоты. Это было бы важно, например, если бы вы пытались измерить ток в приводе с Н-мостом, как показано на Рисунке 7.
Это, вероятно, наиболее сложное применение инструментального усилителя, потому что синфазное напряжение идет от одного рельса к другому, и ток быстро меняется.Важны и ширина полосы, и скорость нарастания.
Программирование
Программирование в этом смысле не означает написание кода; это означает настройку компонента в соответствии с требованиями вашей системы (хотя некоторые усилители имеют традиционные функции программирования с портами и регистрами SPI).
Для ОУ настраиваем часть с отрицательной обратной связью. Это может быть чисто резистивный элемент, но обычно резистор используется с конденсатором, включенным параллельно, чтобы ограничить полосу пропускания.Это помогает улучшить соотношение сигнал / шум, потому что шум будет интегрирован по всему диапазону, даже если мы используем только его часть. Вы также можете использовать конденсаторы сами по себе и получить интегратор или дифференциатор.
Компараторывсегда должны иметь немного положительной обратной связи, чтобы гарантировать, что, как только вход вынуждает выход двигаться, выход усиливает движение (см. Рисунок 4 и рисунок 5). Рисунки и расчеты включены в МТ-083. Некоторые компараторы имеют внутренний гистерезис, но обычно при желании можно добавить больше.Некоторые компараторы с внутренним гистерезисом имеют штырь для добавления резистора для небольшого изменения величины.
Можно использовать операционный усилитель в качестве компаратора, но это не идеально, и есть несколько соображений. Вы должны быть хорошим аналогом, чтобы использовать его в производственной среде. Некоторые соображения содержатся в MT-083, и было написано много статей, за и против. См. Ссылки, если вы любите жить опасно.
Компараторы почти всегда программируются с помощью резисторов.Вы можете добавить резистор большого номинала, чтобы получить немного положительной обратной связи, а также можно использовать конденсатор для обратной связи по переменному току, чтобы избежать гистерезиса постоянного тока. Некоторые компараторы имеют встроенный гистерезис, но его можно увеличить, снова добавив небольшую положительную обратную связь.
Заключительные замечания
При попытке использовать операционный усилитель в качестве компаратора происходят тонкие вещи. Довольно много биполярных операционных усилителей с низким уровнем шума имеют антипараллельные диоды между входами. Диапазон синфазного входного сигнала для большинства компараторов составляет 80% или более от общего диапазона.Но некоторые биполярные операционные усилители с низким уровнем шума имеют один или два диода, включенных последовательно между входами. Это сделано для того, чтобы входной каскад не попадал на стабилитрон одного из переходов базы эмиттера, что со временем ухудшило бы шумовые характеристики.
Таким образом, операционный усилитель на 5 В, используемый в качестве компаратора с пороговым уровнем 3 В для индикатора хорошего питания в системе 3,3 В, будет иметь проблемы с 3 В на одном входе и 0 В на другом, поскольку эти диоды ограничивают максимальное дифференциальное напряжение, допустимое на входах операционного усилителя.
Сводка
Для многих приложений выбор операционного усилителя будет зависеть от того, ориентированы ли вы на точность по постоянному току, точность по переменному току, входное напряжение смещения, полосу усиления или напряжение питания. В 2020 году у вас будет более 700 на выбор. Ключевыми параметрами для компараторов обычно являются задержка распространения и напряжение питания. Выбор немного проще, на выбор 122 детали. Основным критерием для инструментальных усилителей является CMRR как функция частоты, но вблизи постоянного тока также важны напряжение смещения и точность усиления.Поскольку входные усилители являются более специализированной деталью, есть «всего» 63 варианта.
Выбор правильной детали приведет к безотказной и производственной конструкции на долгие годы.
Рекомендации
1 Гарри Холт. «Максимальный ток питания, которого не было». Analog Devices, Inc., ноябрь 2011 г.
2 MT-083 Учебное пособие: «Компараторы». Analog Devices, Inc. 2009.
3 Реза Могими.«Устранение нестабильности компаратора с помощью гистерезиса». Аналоговый диалог , Vol. 34, No. 7, November 2000.
4 Руководство разработчика инструментальных усилителей , 3 rd edition. Analog Devices, Inc. 2006.
Соотношение длин сторон и углов треугольника
Отношение длин сторон и углов треугольника — Math Open Reference В любом треугольнике:- Самая короткая сторона всегда противоположна самой маленькой внутренний угол
- Самая длинная сторона всегда противоположна наибольшему внутреннему углу
Попробуй это Перетащите оранжевые точки на треугольник ниже.
Напомним, что в неравносторонний треугольник, все стороны имеют разную длину и все внутренние углы имеют разные меры. В таком треугольнике самая короткая сторона всегда противоположна самому маленькому углу. (Они выделены жирным шрифтом выше) Точно так же самая длинная сторона противоположна наибольшему углу.
На рисунке выше перетащите любой вершина треугольника и увидишь, какая сторона самая короткая, противоположный угол тоже самый маленький. Затем нажмите «Показать самый большой» и посмотрите, как бы вы ни изменили форму треугольника, самая длинная сторона всегда противоположна наибольшему внутреннему углу.
Средние детали
Если наименьшая сторона противоположна наименьшему углу, а наибольшая — противоположна наибольшему углу, то из этого следует, что поскольку треугольник имеет только три стороны, сторона среднего размера противоположна углу среднего размера.Равносторонние треугольники
Равносторонний треугольник все стороны равны по длине и все внутренние углы равны. Следовательно, в данном случае нет «самого большого» или «самого маленького».Равнобедренные треугольники
Равнобедренные треугольники имеют две стороны одинаковой длины и два равных внутренних угла.Следовательно, могут быть две стороны и углы, которые могут быть «самыми большими» или «самыми маленькими». Если вы будете осторожны с мышью, вы можете создать такую ситуацию на рисунке выше.Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Конгруэнтность и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Неравенства и отношения в треугольнике
Много информации можно получить даже из самых простых характеристик треугольников. В этом разделе мы узнаем о неравенства и отношения внутри треугольника, раскрывающего информацию о сторонах и углах треугольника. Во-первых, давайте взглянем на два существенных неравенства. которые характеризуют треугольники.
Неравенства треугольника
Напомним, что неравенство — это математическое выражение относительного размера или заказ двух предметов. В геометрии мы видим использование неравенств, когда говорим о длине сторон треугольника, или мера углов треугольника. Начнем изучение неравенств треугольника, рассмотрев теорему о неравенстве треугольника.
Теорема о неравенстве треугольника
Сумма длин двух сторон треугольника всегда должна быть больше, чем длина третьей стороны.
Давайте посмотрим, что означает эта теорема в терминах треугольника, который мы имеем ниже.
Теорема о неравенстве треугольника дает три неравенства:
Поскольку на рисунке выполнены все неравенства, мы знаем эти три длины сторон могут образовывать треугольник.
Важно понимать, что каждое неравенство должно выполняться. Если для некоторых причина, треугольник должен был иметь одну сторону, длина которой была больше, чем сумма две другие стороны, у нас будет треугольник с отрезком, который либо слишком короткий (чтобы треугольник не был замкнут) или слишком длинный (чтобы сторона треугольник выходит слишком далеко).
Все наши неравенства не выполняются на приведенной выше диаграмме.Оригинальная иллюстрация показывает незакрашенный рисунок в результате короткого отрезка HG. Если мы повернем сегмент FG to FG ‘, так что сегмент действительно соединяется, образуя замкнутую фигуру, мы видим, что FG ‘слишком длинный.
Теперь мы рассмотрим неравенство, которое касается внешних углов.
Теорема о неравенстве внешнего угла
Размер внешнего угла треугольника больше, чем размер любого из его удаленных внутренних углов.
Для этой теоремы у нас есть только два неравенства, так как мы просто сравниваем внешний угол к двум удаленным внутренним углам треугольника.
Давайте посмотрим, что означает эта теорема с точки зрения иллюстрации, которую мы имеем ниже.
По теореме о неравенстве внешнего угла у нас есть следующие две части информации:
Мы снова воспользуемся этой теоремой в доказательстве в конце этого раздела.Теперь давай изучите некоторые отношения треугольника со стороной угла.
Отношения треугольника
Расположение сторон и углов треугольника очень важно. Мы работали с треугольниками, но одну важную деталь мы, вероятно, упустили это отношение между сторонами и углами треугольника. Эти угловые отношения характеризуют все треугольники, поэтому важно будет понять эти отношения чтобы обогатить наши знания о треугольниках.
Угловые отношения
Если одна сторона треугольника длиннее другой, то угол, противоположный более длинная сторона будет иметь больший градус, чем угол напротив более короткой боковая сторона.
Обратное также верно: если один угол треугольника имеет больший градус, чем другой угол, то сторона, противоположная большему углу, будет длиннее, чем сторона, противоположная меньшему углу.
Короче говоря, нам просто нужно понять, что большие стороны треугольника лежат напротив больших углов, и что меньшие стороны треугольника лежат напротив меньших углы. Давайте посмотрим на рисунки ниже, чтобы наглядно организовать эту концепцию.
Поскольку сегмент BC является самой длинной стороной, угол, противоположный этой стороне,? A, имеет самый большой показатель в? ABC.
Наш наименьший угол,? C, говорит нам, что отрезок AB является самой маленькой стороной? ABC.
Теперь мы можем поработать над некоторыми упражнениями, чтобы использовать наши знания о неравенстве. и отношения внутри треугольника.
Упражнение 1
.На рисунке ниже, какой диапазон длины возможен для третьей стороны, x , быть.
Ответ:
При рассмотрении длин сторон треугольника мы хотим использовать неравенство треугольника . Теорема . Напомним, что эта теорема требует от нас сравнить длину одна сторона треугольника с суммой двух других сторон. Сумма двух стороны всегда должны быть больше длины одной стороны, чтобы фигура быть треугольником.Напишем наше первое неравенство.
Итак, мы знаем, что x должно быть больше 3 . Посмотрим если наше следующее неравенство поможет нам сузить возможные значения x .
Это неравенство показало нам, что значение x может быть не более 17 .Давайте выясним наше окончательное неравенство.
Это последнее неравенство не помогает нам сузить круг возможных вариантов, потому что мы уже осознавая тот факт, что x должно быть больше 3 . Более того, длины сторон треугольников не могут быть отрицательными, поэтому этим неравенством можно пренебречь.
Объединение наших первых двух неравенств дает
Итак, использование теоремы о неравенстве треугольника показывает нам, что x должны иметь длину от 3 до 17 .
Упражнение 2
Перечислите углы в порядке от наименьшего к наибольшему.
Ответ:
В этом упражнении мы хотим использовать информацию, которую мы знаем о угловых отношениях. Поскольку нам предоставлены все длины сторон, нам просто нужно их заказать по порядку от наименьшего к наибольшему, а затем посмотрите на углы, противоположные этим сторонам.
В порядке от меньшего к большему, наши стороны: PQ , QR , и RP .Это означает, что углы, противоположные этим сторонам, будут упорядочены. от наименьшего к наибольшему. Итак, чтобы измерить угол от наименьшего к наибольшему, мы имеем ? R , ? P , а затем ? Q .
Упражнение 3
Какая сторона треугольника ниже самая маленькая?
Ответ:
Чтобы узнать, какая сторона треугольника наименьшая, мы должны сначала вычислить какой угол треугольника наименьший (потому что наименьшая сторона будет быть напротив наименьшего угла).Итак, мы должны использовать теорему о сумме углов треугольника чтобы выяснить меру недостающего угла.
Поскольку ? V имеет наименьший размер, мы знаем, что сторона, противоположная этот угол имеет наименьшую длину. Соответствующая сторона — сегмент DE , так что DE — это самая короткая сторона ? DEV .
Упражнение 4
.
Ответ:
Хотя может быть не сразу понятно, что в таблице приведены два внешних угла. диаграмме, мы должны заметить их, чтобы установить связь между углы двух треугольников. Внешний угол, на котором мы остановимся, составляет ? JKM .
Нам дано, что ? KLM и ? KMJ совпадают, что означает, что мера их углов одинакова.
Мы также знаем, что размер ? JKM больше, чем любой из выносные внутренние углы? KLM. Таким образом, мы знаем, что размер ? JKM больше чем размер ? KLM .
Мы уже установили эквивалентность мер? KLM и ? KMJ , поэтому, но подстановка, мы имеем, что мера ? JKM больше, чем размер ? KMJ . Двухколонный геометрический доказательство нашего аргумента показано ниже.
Упражнение 5 (сложное)
Ответ:
Эта проблема потребует от нас использования нескольких теорем и постулатов. мы практиковали в прошлом.Судя по тому выводу, к которому мы хотим прийти, мы скорее всего, придется также использовать теорему о неравенстве треугольника .
Начнем с того, что заметим, что сегменты AD и BE параллельны. Этот факт позволяет нам утверждать, что ? A соответствует ? E . по теореме об альтернативном внутреннем угле (с сегментом AE как трансверсаль, касающаяся множества параллельных линий).
Нам также сообщили, что C является средней точкой сегмента AE . Это говорит нам, что AC и CE равны по длине, потому что средние точки отмечают середину отрезка линии.
Далее, мы можем сказать, что ? ACD и ? ECB совпадают, поскольку это вертикальные углы.Другими словами, у них одинаковый размер угла.
Согласно постулату ASA , мы можем сказать, что ? ACD ?? ECB , поскольку у нас есть две пары конгруэнтных углов и одна пара конгруэнтных сторон.
Теперь обратим внимание на ? ACD . Теорема о неравенстве треугольника , который гласит, что сумма длин двух сторон треугольника должна быть больше чем длина третьей стороны, помогает нам показать, что сумма сегментов AC и CD больше, чем длина AD .
Мы знаем, что CD и CB равны по длине, так как они являются соответствующими частями равных треугольников, поэтому мы можем заменить CB в для CD , чтобы прийти к нашему выводу. Потому что информации много чтобы следовать, у нас есть новая иллюстрация этой проблемы ниже, которая показывает конгруэнтные стороны и углы.

