Как работает эквивалентная схема диода. Какие существуют модели для описания характеристик диодов. Чем отличаются кусочно-линейная, упрощенная и идеальная схемы замещения диода. Как рассчитать параметры эквивалентной схемы реального диода.
Что такое эквивалентная схема диода и зачем она нужна
Эквивалентная схема диода — это упрощенная модель, описывающая поведение реального полупроводникового прибора с помощью идеальных элементов. Она позволяет анализировать работу диода в электрических цепях, не прибегая к сложным физическим уравнениям.
Основные цели использования эквивалентных схем диодов:
- Упрощение расчетов электрических цепей с диодами
- Анализ работы диода в различных режимах
- Определение ключевых параметров диода
- Моделирование поведения диода в САПР
Эквивалентная схема позволяет заменить сложный полупроводниковый прибор набором простых элементов — резисторов, конденсаторов, источников тока и напряжения. При этом внешние характеристики такой схемы замещения должны максимально точно соответствовать характеристикам реального диода.
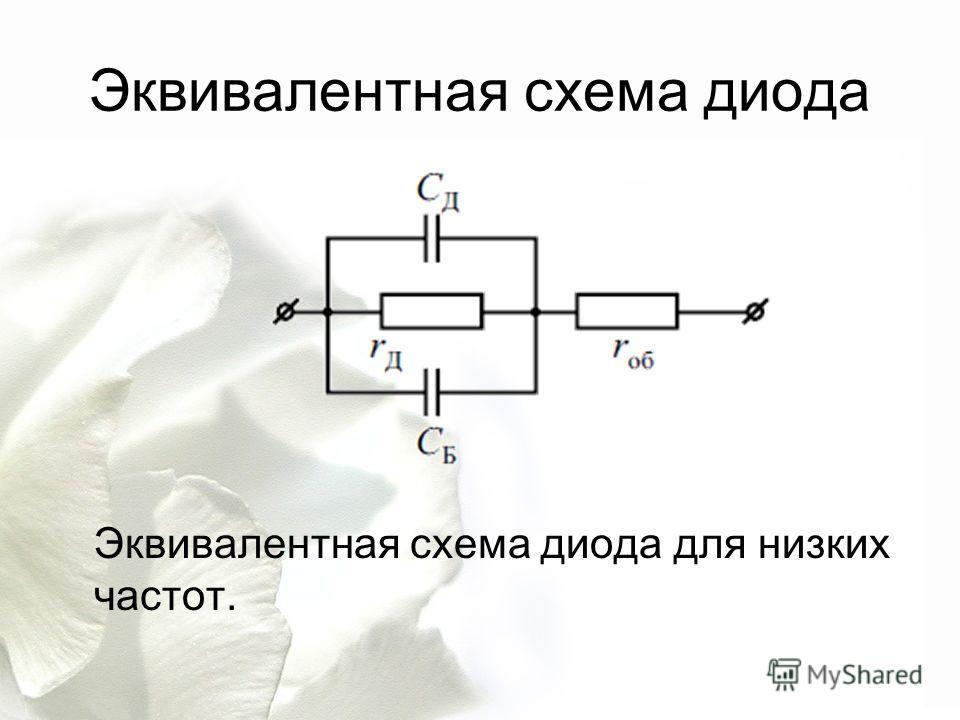
Основные модели эквивалентных схем диодов
Существует несколько основных моделей эквивалентных схем диодов, отличающихся сложностью и точностью:
1. Идеальная модель диода
Самая простая модель, представляющая диод как идеальный ключ:
- При прямом смещении — короткое замыкание (нулевое сопротивление)
- При обратном смещении — разрыв цепи (бесконечное сопротивление)
Такая модель пригодна только для приближенных расчетов в цифровых схемах.
2. Кусочно-линейная модель
Аппроксимирует вольт-амперную характеристику диода отрезками прямых линий. Обычно содержит:
- Идеальный диод
- Источник ЭДС (напряжение открытия диода)
- Резистор (дифференциальное сопротивление открытого диода)
Эта модель хорошо подходит для ручных расчетов и анализа работы диода в ключевом режиме.
3. Полная эквивалентная схема диода
Наиболее точная модель, учитывающая основные физические процессы в p-n переходе:- Нелинейное сопротивление перехода
- Барьерная и диффузионная емкости
- Объемное сопротивление полупроводника
- Генерационно-рекомбинационные процессы
Такая модель применяется для точного моделирования в САПР и расчета высокочастотных схем.
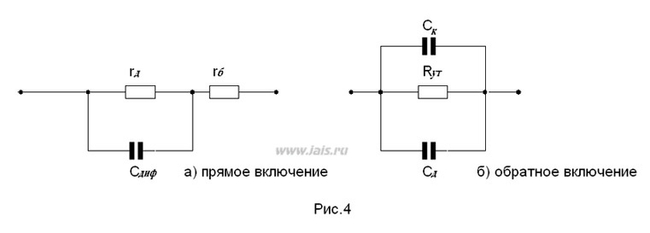
Кусочно-линейная эквивалентная схема диода
Кусочно-линейная модель является компромиссом между простотой и точностью. Она аппроксимирует реальную вольт-амперную характеристику диода тремя отрезками прямых:
- Участок обратного тока
- Участок нарастания прямого тока
- Линейный участок прямого тока
Эквивалентная схема содержит следующие элементы:
- Идеальный диод VD
- Источник ЭДС E (напряжение открытия диода, обычно 0.6-0.7 В для кремния)
- Резистор R (дифференциальное сопротивление открытого диода)
Преимущества кусочно-линейной модели:
- Простота расчетов
- Наглядность
- Достаточная точность для большинства практических задач
Недостатки:
- Не учитывает плавный изгиб ВАХ в области малых токов
- Не описывает температурную зависимость параметров
- Не применима для высокочастотного анализа
Параметры полной эквивалентной схемы реального диода
Полная эквивалентная схема учитывает основные физические процессы в p-n переходе и содержит следующие элементы:
1. Нелинейное сопротивление перехода
Моделируется экспоненциальной зависимостью тока от напряжения:
I = Is(e^(U/φт) — 1)
где:
- Is — ток насыщения
- φт — температурный потенциал (kT/q)
2. Барьерная емкость Cб
Обусловлена изменением ширины обедненного слоя при изменении напряжения. Зависит от напряжения обратно пропорционально:
Cб = C0 / (1 — U/φk)^n
где:
- C0 — емкость при нулевом смещении
- φk — контактная разность потенциалов
- n — коэффициент (0.33-0.5)
3. Диффузионная емкость Cд
Связана с накоплением неосновных носителей в базе диода при прямом смещении. Пропорциональна прямому току:
Cд = τ * (dI/dU)
где τ — время жизни неосновных носителей
4. Объемное сопротивление базы Rб
Учитывает сопротивление нейтральных областей полупроводника. Обычно составляет единицы Ом.
5. Ток утечки Iут
Моделирует генерационно-рекомбинационные процессы в обедненном слое. Имеет слабую зависимость от напряжения.
Расчет параметров эквивалентной схемы диода
Для определения параметров эквивалентной схемы реального диода используются следующие методы:
1. Анализ статической вольт-амперной характеристики
По наклону прямой ветви ВАХ в области больших токов определяется дифференциальное сопротивление Rд. Напряжение открытия Uпр соответствует точке пересечения касательной к ВАХ с осью напряжений.

2. Измерение емкости перехода
Барьерная емкость измеряется при обратном смещении диода на низкой частоте. Диффузионная емкость определяется из измерений полной емкости при прямом смещении.
3. Анализ переходных характеристик
По времени восстановления обратного сопротивления диода можно оценить время жизни неосновных носителей и диффузионную емкость.
4. Температурные измерения
Зависимость тока насыщения от температуры позволяет определить ширину запрещенной зоны полупроводника.
5. Высокочастотные измерения
По частотным зависимостям импеданса диода уточняются значения емкостей и сопротивлений эквивалентной схемы.
Полученные параметры позволяют построить точную эквивалентную схему, пригодную для моделирования работы диода в широком диапазоне режимов.
Применение эквивалентных схем диодов
Эквивалентные схемы диодов широко используются в следующих областях:
1. Расчет электронных схем
Упрощенные модели позволяют быстро рассчитать рабочие точки и основные характеристики схем с диодами.
2. Компьютерное моделирование
Точные эквивалентные схемы применяются в САПР для анализа сложных электронных устройств.
3. Разработка новых приборов
Эквивалентные схемы помогают оптимизировать параметры полупроводниковых структур.
4. Диагностика неисправностей
Сравнение измеренных характеристик с моделью позволяет выявить дефекты диодов.
5. Обучение
Эквивалентные схемы наглядно демонстрируют принципы работы полупроводниковых приборов.
Таким образом, эквивалентные схемы являются мощным инструментом анализа и расчета диодов, значительно упрощающим работу инженеров-электронщиков.
Выпрямительные диоды. Схемы замещения диода для прямого и обратного включения, страница 2
Из-за сложности аналитического представления токов и напряжений в реальных схемах с диодами на практике часто используется графоаналитический метод решения задач.
Пример: определить падение напряжения на открытом диоде VD, ток I, rДИФ в схеме, представленной на рис. 9.3.2, б. Известна ВАХ диода (рис.8.2, в), UП = 2 В, R = 1 кОм.
Рис. 8.3.2 Обозначение диода (а), схема включения диода (б), иллюстрация
графического метода определения тока через диод и напряжения на нем (в)
При решении используется 2-ой закон Кирхгофа для цепи (рис. 8.3.2, б):
(8.3.2)
Это уравнение
прямой линии (нагрузочная прямая), которая строится по двум точкам ее
пересечения с осями координат. Напряжение холостого хода UХХ – это точка
пересечения оси абсцисс и нагрузочной прямой: UХХ = UП = 2 В. Ток
короткого замыкания IКЗ – точка
пересечения прямой с осью ординат: IКЗ = U
П/R = 2 мА. Связь
между I и UПР диода
определяется ВАХ.
Напряжение холостого хода UХХ – это точка
пересечения оси абсцисс и нагрузочной прямой: UХХ = UП = 2 В. Ток
короткого замыкания IКЗ – точка
пересечения прямой с осью ординат: IКЗ = U
П/R = 2 мА. Связь
между I и UПР диода
определяется ВАХ.
Рабочая точка «А» пересечения прямой с ВАХ является графическим решением задачи: I = 1 мА; UПР = 1 В.
Для расчета дифференциального сопротивления диода нужно провести касательную к ВАХ в рабочей точке и определить значения DU и DI как проекции на соответствующие оси:
Этот метод удобно применять для сложных схем, содержащих много элементов.
В простых
задачах используются только аналитические зависимости и схемы замещения диода
для прямого включения (рис.9.3.3, а) и обратного включения (рис.9.3.3, б).
Характеристики диодов, указанные на рисунке, берутся из справочной литературы.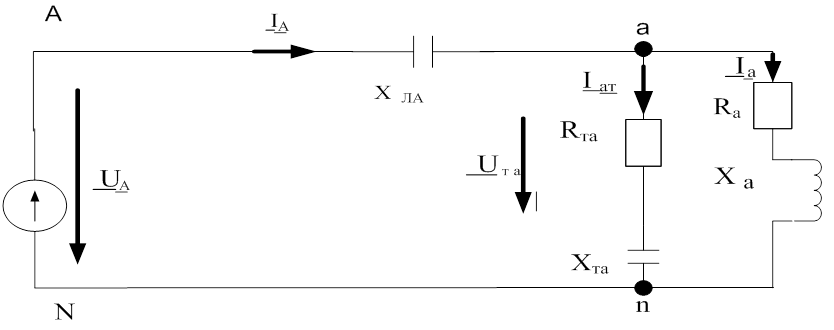
Рис. 8.3.3 Схемы замещения диода
для прямого включения (а) и обратного включения (б).
Пример: при комнатной температуре прямой ток через германиевый диод составляет I = 1А. Найти, при каком напряжении ток через диод будет равен 1% от величины I. Значение IОБР = 3 мкА.
Выражение 8.3.1 для комнатной температуры можно записать в следующем виде:
(8.3.3)
где: e – основание показательной функции.
Ответ: U = 0,2 В.
Основная зависимость обратного тока от материала полупроводника определяется шириной запрещенной зоны DW, так как она стоит в экспоненте:
(8.
Поэтому для расчета изменений обратного тока или соотношения этой величины у различных диодов достаточно использовать выражение 8.3.4.
Обозначение полупроводниковых диодов
Обозначение состоит из 6-ти элементов (ГОСТ 10862-72):
1 элемент – это буква, указывающая на основе какого материала выполнен диод (Г или 1 – германий, К или 2 – кремний, А или 3 – соединения галлия, например, арсенид галлия, И или 4 – соединения индия). Цифрами обозначаются приборы военной приемки, буквами приборы коммерческого назначения.
2 элемент – буква, обозначающая подклассы диода. Выпрямительные, высокочастотные, импульсные и универсальные – Д. А – сверхвысокочастотные. Варикапы – В. Туннельные – И. Стабилитроны – С. И – туннельные. Ф – фотодиоды. Л – светодиоды. Ц – выпрямительные столбы и блоки.
3 элемент – цифра, определяющая назначение диода. Для выпрямительных диодов: 1 – IПР.MAX ≤ 0,3А; 2 – 0,3А ≤
 MAX ≤ 10А. У стабилитронов определяет мощность
рассеяния.
MAX ≤ 10А. У стабилитронов определяет мощность
рассеяния.4 и 5 элементы – цифры, определяющие номер разработки, у стабилитронов напряжение стабилизации.
6 элемент – буква, показывающая деление технологического типа на параметрические группы (модификации диодов), у стабилитронов порядковый номер разработки.
Примеры характеристик выпрямительных диодов
|
Наименование |
UОБР., В |
IПР.max, A |
IОБР. max, мкА |
FD max, кГц |
|
КД102А |
250 |
0.1 |
0.1 |
10 |
|
КД102Б |
300 |
0. |
1 |
10 |
|
КД103А |
50 |
0.1 |
0.5 |
20 |
|
КД105В |
600 |
0.3 |
100 |
1 |
|
КД209Г |
1000 |
0.2 |
50 |
1 |
|
КД521Д |
12 |
0.05 |
1 |
100000 |
|
КД522Б |
50 |
0. |
5 |
100000 |
|
КД2997В |
50 |
30 |
200 |
100 |
Полупроводниковых диодов — Студопедия
Поделись с друзьями
Математические модели и эквивалентные схемы реальных
Математические модели и эквивалентные схемы реальных полупроводниковых диодов
Полупроводниковые диоды
ЛЕКЦИЯ 2
План лекции:
2.2. Расчёт рабочей точки полупроводникового диода в статическом режиме
2.1.1. Модель реального p-n-перехода в статическом режиме работы
В реальном p-n-переходе в обеднённом слое имеют место как генерация, так и рекомбинация носителей зарядов, т. е. первое допущение, принятое для идеализированного p-n-перехода, не выполняется. В этом случае вольтамперную характеристику диода описывают формулой, в которую вводят коэффициент , учитывающий неидеальность обеднённого слоя:
е. первое допущение, принятое для идеализированного p-n-перехода, не выполняется. В этом случае вольтамперную характеристику диода описывают формулой, в которую вводят коэффициент , учитывающий неидеальность обеднённого слоя:
Так как нелинейными свойствами обладает обеднённый слой, то собственно неидеальность p-n-перехода можно выразить как
Кроме того, электрические сопротивления и нейтральных p— и
Суммарное сопротивление , учитывающее свойства нейтральных p— и n-областей, называют базовым сопротивлением диода.
Рис. 2.1. Структура (а) и эквивалентная схема реального полупроводникового диода с p-n-переходом (б)
На базовом сопротивлении при протекании тока имеет место падение напряжения . Поэтому формула (2.1) может быть преобразована к виду
Поэтому формула (2.1) может быть преобразована к виду
Вольтамперная характеристика полупроводникового диода с реальным p-n-переходом приведена на рис. 2.2.
С ростом прямого тока падение напряжения на базовой области диода может стать сравнимым с напряжением на p-n-переходе, т.е. . При этом на ВАХ диода появится почти линейный участок. При дальнейшем увеличении прямого тока сопротивление начинает уменьшаться из-за увеличения концентрации инжектированных в базу носителей заряда. ВАХ снова начнёт отклоняться от прямой линии. Это явление называют эффектом модуляции сопротивления базы. Однако данный эффект учитывать не будем.
Рис. 2.2. Вольтамперная характеристика полупроводникового диода (1 − с идеализированным p-n-переходом, 2 – с учётом неидеальности () обеднённого слоя, 3 – с реальным p-n-переходом)
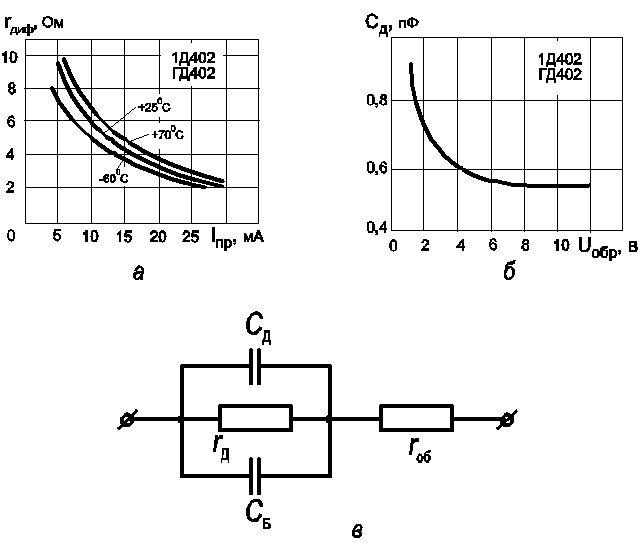
Величины и непосредственно в справочных данных не приводят. Поэтому значения этих параметров надо вычислять по формуле (2.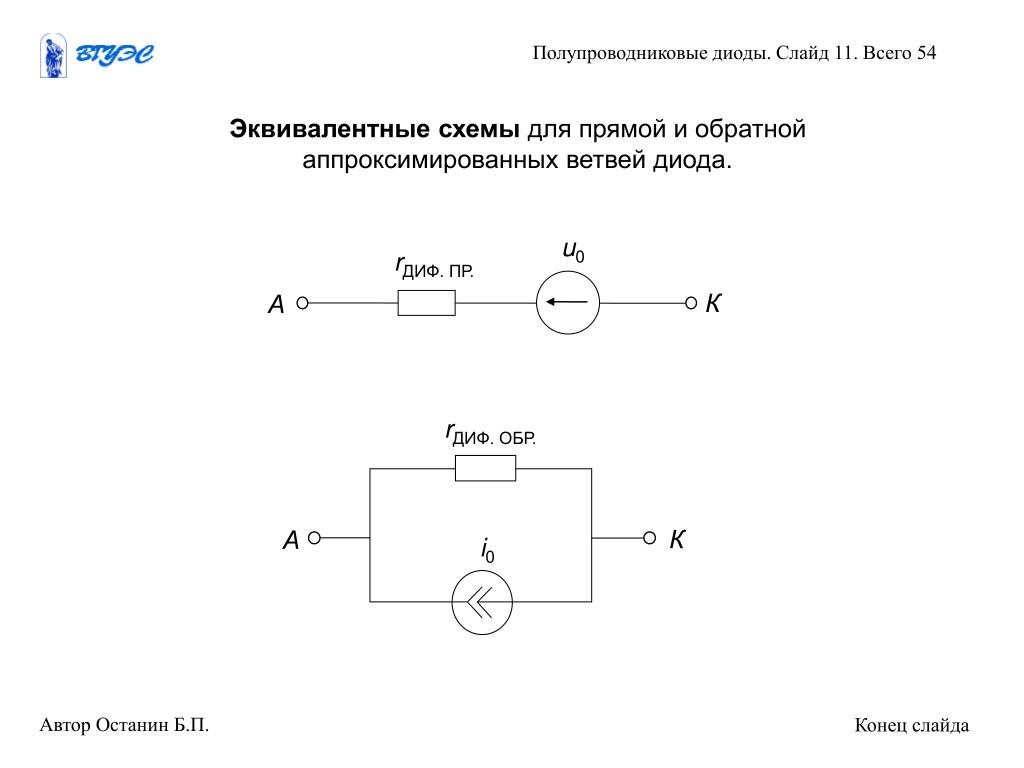 3), используя семейство характеристик , приводимых в отдельных справочниках в виде графиков для конкретного типа диода.
3), используя семейство характеристик , приводимых в отдельных справочниках в виде графиков для конкретного типа диода.
2.1.2. Модели идеализированного и реального p-n-переходов в динамическом режиме работы
В динамическом режиме работы важную роль играют дифференциальное сопротивление и ёмкость p-n-перехода.
Дифференциальное сопротивление представляет собой величину, обратную крутизне вольтамперной характеристики p-n-перехода.
Преобразуя формулу (2.1) для идеализированного p-n-перехода к виду
получаем выражение
Здесь и в дальнейшем для простоты будем обозначать как .
Для реального p-n-перехода из преобразованной формулы (2.2) имеем
и выражение
При дифференциальное сопротивление больше статического, а при имеет место обратное соотношение (рис. 2.3).
Рис. 2.3. Сравнительные характеристики статического и дифференциального сопротивлений полупроводникового диода
Границами обеднённого слоя являются равные по величине, но противоположные по знаку электрические заряды ионов акцепторов и доноров.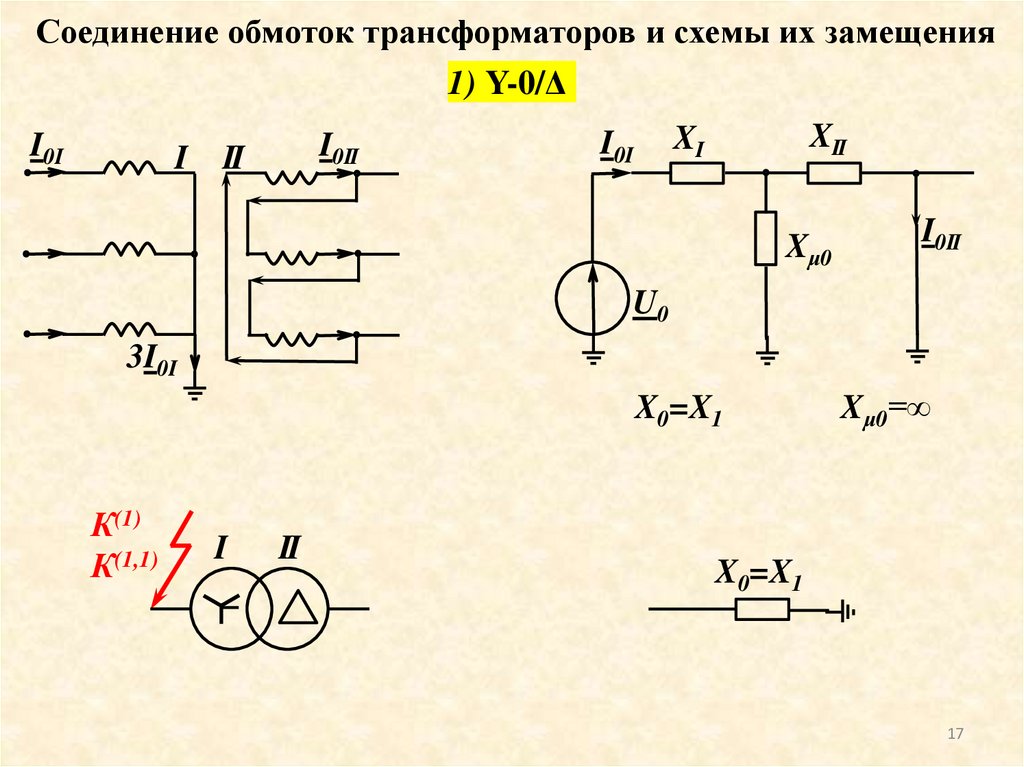 Между границами существует разность потенциалов или потенциальный барьер. Поэтому по определению эта область p-n-перехода обладает ёмкостью, называемой барьерной:
Между границами существует разность потенциалов или потенциальный барьер. Поэтому по определению эта область p-n-перехода обладает ёмкостью, называемой барьерной:
Здесь − значение барьерной ёмкости при , − контактная разность потенциалов, которую можно принять равной , для резкого p-n-перехода и для плавного p-n-перехода.
Кроме того, в реальном p-n-переходе в p— и n-областях имеются движущиеся заряды, а на сопротивлениях и имеет место падение напряжений. Следовательно, существует ещё одна ёмкость, называемая диффузионной, так как заряды в p— и n-областях движутся благодаря диффузии.
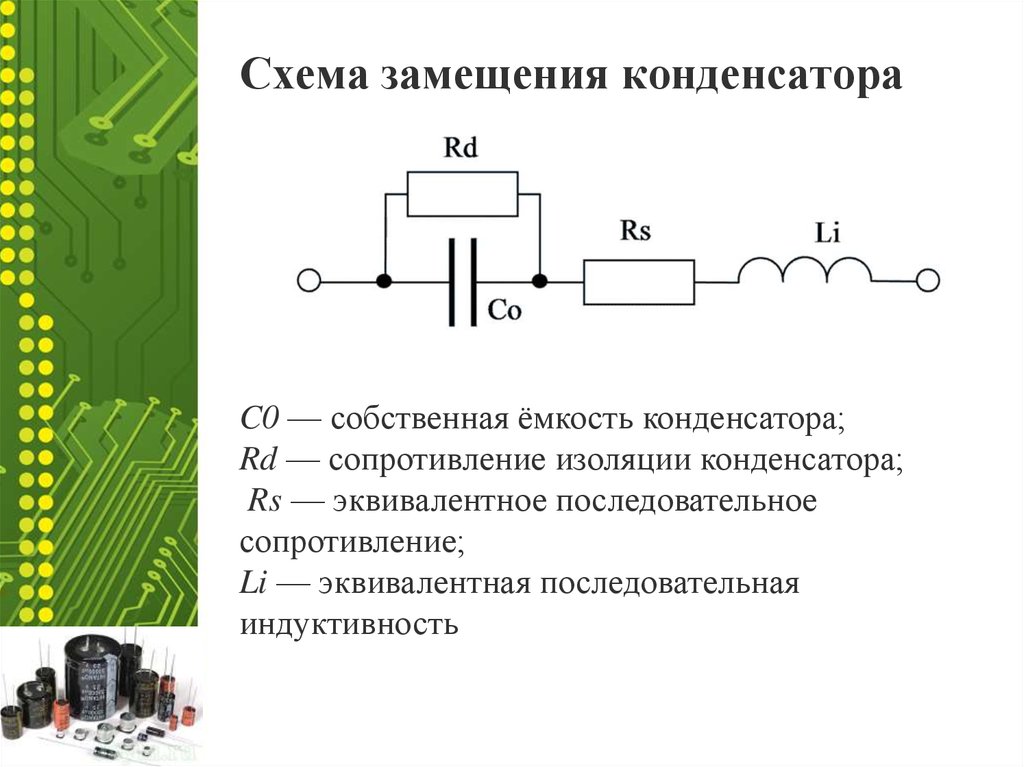
Барьерная и диффузионная емкости составляют ёмкость реального p-n-перехода, причём . Несмотря на то, что ёмкости образованы в разных частях p-n-перехода, в эквивалентной схеме они объединены в одну, параллельную реальному (неидеальному диоду) − рис. 2.4 а.
Рис. 2.4. Эквивалентные схемы реального p-n-перехода (а) и реального полупроводникового диода (б) в динамическом режиме работы (диапазон высоких частот)
Реальный диод как конструктивный элемент схемы обладает паразитной ёмкостью корпуса и паразитной индуктивностью выводов. В диапазоне высоких частот паразитной индуктивностью можно пренебречь (рис. 2.4 б), а в диапазоне сверхвысоких частот необходимо учитывать оба паразитных параметра (рис. 2.5).
В диапазоне высоких частот паразитной индуктивностью можно пренебречь (рис. 2.4 б), а в диапазоне сверхвысоких частот необходимо учитывать оба паразитных параметра (рис. 2.5).
Рис. 2.5. Эквивалентная схема реального полупроводникового диода в динамическом режиме работы (диапазон свч)
2.2. Расчёт рабочей точки полупроводникового диода в
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Эквивалентные схемы диодовЭквивалентная схема
фактические терминальные характеристики устройства. Проще говоря, это просто означает, что диод в цепи можно заменить другими элементами без существенного влияния на поведение цепи. Диод можно смоделировать тремя различными способами в зависимости от требуемой точности. Ниже перечислены три модели с возрастающей точностью:
1. Кусочно-линейная эквивалентная схема
Метод получения эквивалентной схемы для диода заключается в аппроксимации характеристик устройства отрезками прямой линии.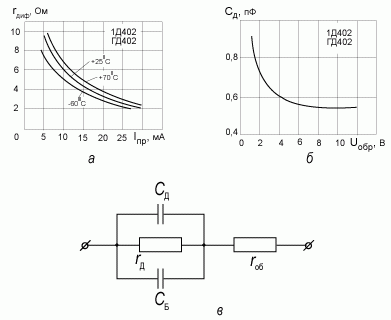 Полученная эквивалентная схема естественно называется кусочно-линейной эквивалентной схемой
Полученная эквивалентная схема естественно называется кусочно-линейной эквивалентной схемой
Понятно, что кусочно-линейные характеристики не совсем точно отражают характеристики диода, особенно вблизи колена кривой. Однако он обеспечивает хорошее первое приближение к фактическим характеристикам диода. Кусочно-линейные характеристики можно получить, заменив диод в цепи резистором, батарейкой и идеальным диодом.
2. Упрощенная эквивалентная схема
Эквивалентная модель в данном случае состоит из батареи и идеального диода. Рассмотрим горизонтальную линию от (0 до 0,7 В) на кривой. Горизонтальная линия показывает, что ток, протекающий через диод, равен нулю при напряжении от 0 до 0,7 В.
Упрощенная эквивалентная схема Чтобы смоделировать такое поведение, мы поместили батарею на 0,7 В в эквивалентную модель диода. Это не означает, что диоды являются источником напряжения. При измерении напряжения на изолированном диоде прибор покажет нулевое значение. Батарея просто указывает, что она препятствует протеканию тока в прямом направлении до 0,7 В. Когда напряжение становится больше 0,7 В, ток начинает течь в прямом направлении.
Батарея просто указывает, что она препятствует протеканию тока в прямом направлении до 0,7 В. Когда напряжение становится больше 0,7 В, ток начинает течь в прямом направлении.
3. Модель идеального диода
На рисунке показано, что падение напряжения на диоде равно нулю при любом значении тока диода. Идеальный диод не пропускает ток при обратном смещении. Ток, протекающий через диод, равен нулю при любом значении напряжения обратного смещения. Принимая это во внимание, идеальный диод можно представить как открытый или закрытый ключ в зависимости от напряжения смещения.
Идеальный диод Модель- Идеальный диод допускает протекание прямого тока при любом значении напряжения прямого смещения. Следовательно, идеальный диод можно смоделировать как замкнутый переключатель в условиях прямого смещения. Это показано на рисунке.
- Идеальный диод обеспечивает нулевой ток в условиях обратного смещения. Следовательно, его можно смоделировать как открытый переключатель.
 Это указано на рисунке.
Это указано на рисунке.
Теги: приводы, продвинутый, Arduino, основы, Конденсатор, коды, Диод, легко, электричество, Электроника для детей, Электроника, Электроника для детей, Электроника упрощенная, техника для детей, ESP, ESP32, ESP8266, google, Резистор, робототехника, Безопасность , датчики, простой, Простой Arduino, Упрощенный, Транзистор
Совместное моделирование производительности PV | Модели эквивалентных схем с одним диодом
Эквивалентные модели цепей определяют всю ВАХ ячейки, модуля или массива как непрерывную функцию для заданного набора рабочих условий. Одной из широко используемых базовых моделей эквивалентной схемы является модель с одним диодом, которая основана на физических принципах (например, Gray, 2011) и представлена следующей схемой для одиночного солнечного элемента:
Основное уравнение для этой эквивалентной схемы формулируется с использованием закона тока Кирхгофа для тока :
Здесь представляет световой ток в ячейке, представляет зависящий от напряжения ток, теряемый на рекомбинацию, и представляет ток, теряемый из-за шунтирующих сопротивлений. В этой модели с одним диодом моделируется с помощью уравнения Шокли для идеального диода:
В этой модели с одним диодом моделируется с помощью уравнения Шокли для идеального диода:
, где — коэффициент идеальности диода (безразмерный, обычно от 1 до 2 для ячейки с одним переходом), — ток насыщения, а — тепловое напряжение определяется по:
где – постоянная Больцмана, – элементарный заряд .
Запись тока шунта в виде и объединение этого и приведенного выше уравнений приводит к полному основному уравнению для модели с одним диодом:
Пять параметров в этом уравнении являются основными для всех моделей эквивалентных схем с одним диодом:
- : световой ток (А)
- : обратный ток насыщения диода (А)
- : последовательное сопротивление ()
- : шунтовое сопротивление ()
- : коэффициент идеальности диода (безразмерный)
Для фотогальванического модуля или массива, состоящего из элементов, расположенных последовательно, и при условии, что все элементы идентичны и находятся под одинаковым и одинаковым излучением и температурой (т. е. генерируют одинаковый ток и напряжение), и
е. генерируют одинаковый ток и напряжение), и
. Уравнение для одного диода для модуля или массива принимает вид ( Tian, 2012):
где и — ток и напряжение соответственно модуля или массива. Следует соблюдать осторожность при реализации параметров модели, поскольку они применимы к ячейке, модулю или массиву. Параметры для модулей или массивов строго используются с уравнением для одного диода для , которое является наиболее часто реализуемой формой.
В некоторых реализациях (например, De Soto et al., 2006) тепловое напряжение , коэффициент идеальности диода и количество последовательно соединенных элементов объединены в одну переменную, называемую модифицированным коэффициентом идеальности:
.
Содержание этой страницы предоставлено Мэтью Бойдом (NIST) и Клиффордом Хансеном (Sandia)
Описаны следующие модели эквивалентных схемных модулей. Эти модели были предложены с различными наборами вспомогательных уравнений, которые описывают, как основные параметры уравнения для одного диода изменяются в зависимости от температуры ячейки и освещенности.

 1
1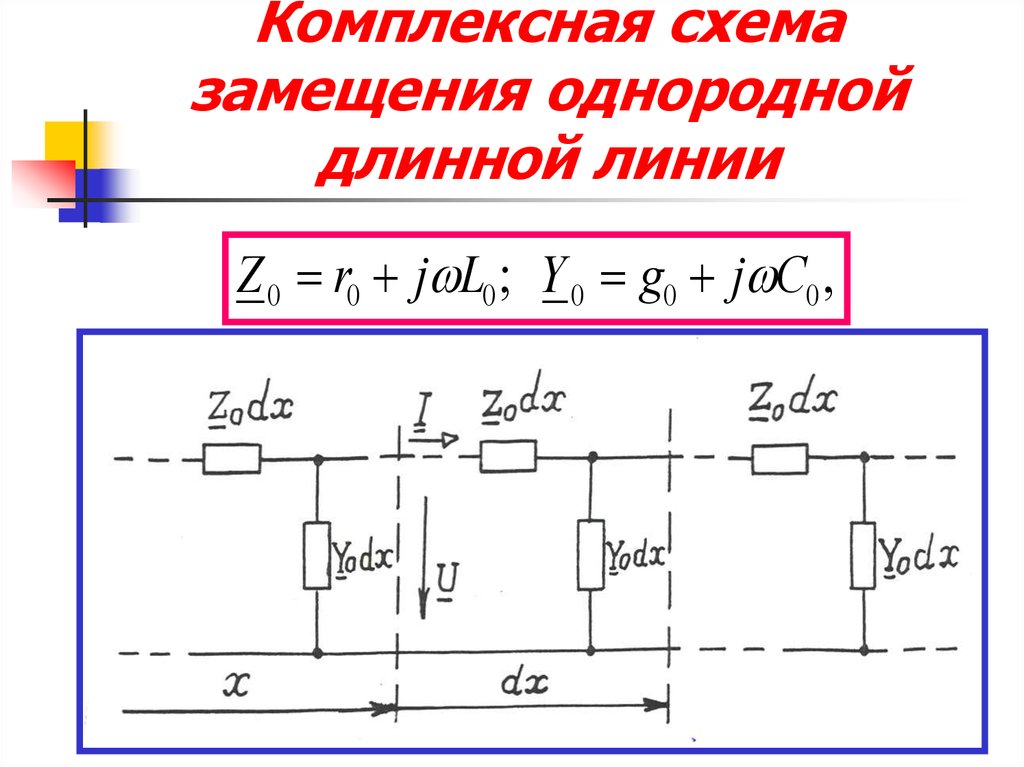 1
1