Неинвертирующий усилитель
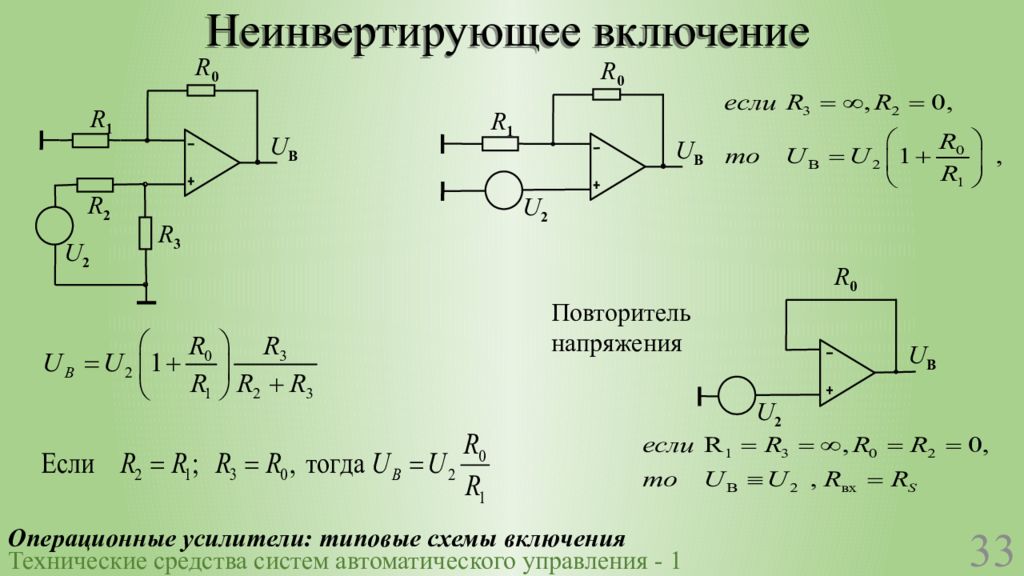
В схеме инвертирующего усилителя рис. 1.5 резисторы R1 и R2 образуют делитель, через который протекает одинаковый токИсходя из этого к инвертирующему входу ОУ приложено напряжение:
Рисунок 1.1 — Неинвертирующий усилитель
Однако, как уже отмечалось, за счет отрицательной обратной связи потенциалы инвертирующего и неинвертирующего входов будут примерно равными, т.е.
Отсюда коэффициент усиления неинвертирующего усилителя:
В отличие от инвертирующего усилителя входное сопротивление неинвертирующего усилителя определяется входным дифференциальным сопротивлением ОУ и можно считать, что
(Например, у усилителей с МОП транзисторами на входе Ом. Выходное сопротивление составляет несколько десятков-сотен Ом. Сумма сопротивлений (R1 +R2) должна быть такой, чтобы общий максимальный ток нагрузки ОУ с учетом этого сопротивления не превышал допустимого значения.
Рисунок 1.
На рис. 1.2 приведена схема неинвертирующего усилителя со 100% отрицательной обратной связью. При подаче напряжения на вход, за счет обратной связи выходное напряжение будет изменяться до тех пор, пока потенциалы инвертирующего и неинвертирующего входов не сравняются (считаем ), т.е выходное напряжение окажется приблизительно равным входному. Таким образом коэффициент усиления схемы рис. 6.7
В силу этого схема рис. 1.2 называется повторителем, так как сигнал на выходе имеет ту же амплитуду и фазу , что и входной. Повторитель часто используется в качестве буферного каскада.
При необходимости усиливать переменный сигнал можно использовать схему рис. 1.3. Для входного тока (очень небольшого) в схеме предусмотрено заземление неинвертирующего входа через резистор R. RC-цепь образует фильтр высоких частот, поэтому постоянная времени должна выбираться исходя из требуемой нижней граничной частоты пропускания усилителя.
Рисунок 1.
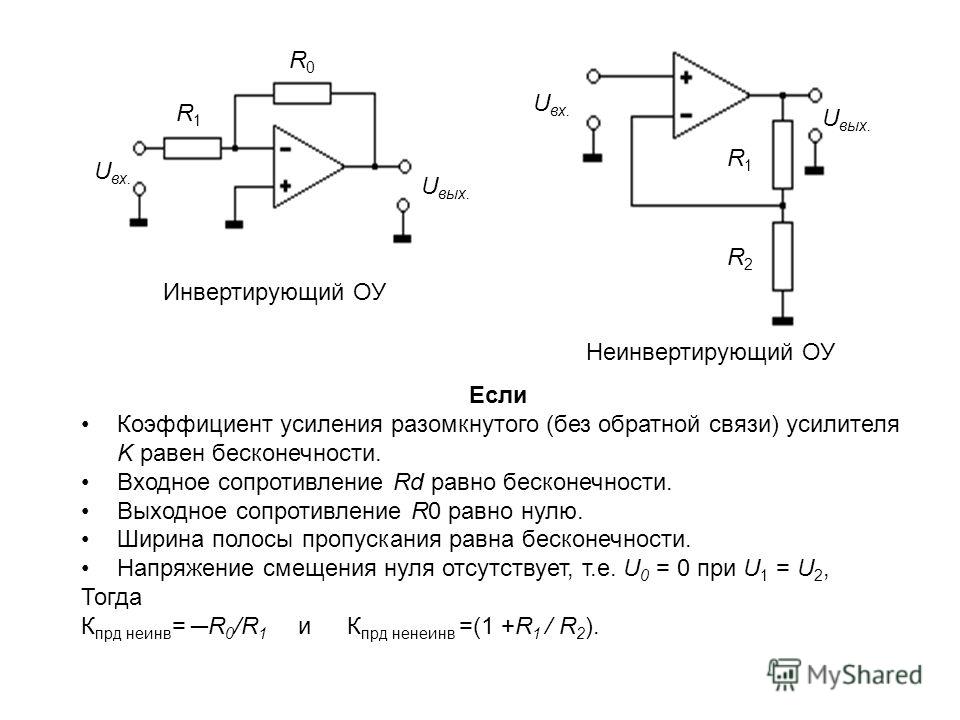3 – Усилитель переменного напряжения Аналогия для делителя в цепи обратной связи
Добавлено 23 ноября 2018 в 02:15
Сохранить или поделиться
Полезной аналогией для понимания схем усилителей с делителем напряжения в цепи отрицательной обратной связи является механический рычаг с относительным движением концов рычага, представляющих изменение входных и выходных напряжений, и опорной точкой (точкой поворота), представляющей место точки земли, реальной или виртуальной.
Возьмем, к примеру, следующую неинвертирующую схему на операционном усилителе. Из предыдущей статьи известно, что коэффициент усиления неинвертирующего усилителя никогда не может быть меньше единицы (1). Если мы нарисуем рычаг рядом со схемой усилителя, с расстояниями между точкой опоры и концами рычага, символизирующими значения резисторов, движение рычага будет означать изменение напряжения на входных и выходных клеммах усилителя:
Физики называют этот тип рычага, с входной силой (усилием), прикладываемой между точкой опоры и выходом (нагрузкой), рычагом третьего рода.
Он характеризуется смещением (движением) выхода, по меньшей мере, большим, чем смещение входа («усиление», по меньшей мере, 1), и в том же направлении. Применение положительного входного напряжения к этой схеме на ОУ аналогично смещению «входной» точки на рычаге вверх:
Из-за характеристик рычага, усиливающих смещение, точка «выхода» будет перемещаться в два раза дальше, чем точка «входа», и в том же направлении. В электронной цепи выходное напряжение будет в два раза больше входного напряжения и с той же полярностью. Применение отрицательного входного напряжения аналогично движению рычага вниз от его «нулевого» положения, что приводит к усиленному выходному смещению, которое так же отрицательно:
Неинвертирующий усилитель с отрицательным входным напряжением. Аналогия с рычагомЕсли изменить отношение резисторов R2/R1, мы изменим коэффициент усиления схемы на операционном усилителе.
В терминах рычагов это означает перемещение входной точки относительно точки опоры и конца рычага, что аналогичным образом изменяет «коэффициент усиления» смещения механизма:
Теперь любой входной сигнал будет усиливаться в четыре раза, а не в два:
Неинвертирующий усилитель, изменение коэффициента усиления по напряжению. Аналогия с рычагомПри одинаковых номиналах резисторов (равные длины рычага с каждой стороны от точки опоры) выходное напряжение (смещение) будет равным по величине входному напряжению (смещению), но противоположной полярности (направления).
Положительный входной сигнал приводит к отрицательному выходному сигналу:
Однако с инвертирующей схемой усилителя возможны коэффициенты усиления менее 1, как и у рычагов первого класса. Перемена местами номиналов R2 и R1 аналогична перемещению точки опоры в противоположное положение на рычаге относительно центра: одна треть от выходного конца. Теперь выходное смещение будет составлять половину от входного смещения.
Теги
Делитель напряженияИнвертирующий усилительКоэффициент усиления по напряжениюНеинвертирующий усилительОбучениеОтрицательная обратная связьОУ (операционный усилитель)ЭлектроникаСохранить или поделиться
8.4. Применение операционных усилителей | Электротехника
Операционный усилитель является базовым элементом устройств аналоговой обработки сигналов и применяется в самых разнообразных схемах. На основе операционных усилителей (ОУ) создаются схемы, предназначенные для выполнения математических операций над входными сигналами (сложения, вычитания, интегрирования, выделения модуля функции и т.п.). Такие схемы находят широкое применение в устройствах автоматического управления.
Наиболее распространенными являются суммирующие и интегрирующие схемы на ОУ, а также ряд схем, в которых ОУ используются в нелинейном режиме (мультивибратор, одновибратор, генератор линейно изменяющегося напряжения и т.д.).
Главным недостатком ОУ является нестабильность коэффициента усиления, который в полупроводниковых усилителях очень сильно зависит от режима работы, в первую очередь от температуры, и меняется от экземпляра к экземпляру в очень широких пределах. Кроме того, линейный участок АЧХ ограничен весьма малыми значениями входных напряжений. Поэтому ОУ используются с цепями обратной связи.
Основными схемами на ОУ являются инвертирующий и неинвертирующий усилители, режим работы которых осуществляется в пределах линейного участка передаточной характеристики. Любое схемотехническое решение с применением ОУ содержит одно из таких включений. Также весьма важны схемы компенсации напряжения сдвига
При анализе схем на ОУ обычно принимают следующие упрощающие предположения
· коэффициент усиления стремится к бесконечности;
· входы ОУ не потребляют тока;
· входное сопротивление стремиться к бесконечности;
· напряжение между входами равно нулю.
Неинвертирующий усилитель на ОУ
В неинвертирующем усилителе (рис. 8.10) коэффициент усиления всей схемы по напряжению может быть жестко задан с помощью сопротивлений R1 и Rос. В данной схеме входной сигнал подается на неинвертирующий вход ОУ. Усилитель содержит последовательную отрицательную обратную связь по напряжению, создаваемую на резисторе Rос и поданную на инвертирующий вход. Схема обладает высоким полным входным сопротивлением.
Выражение для коэффициента усиления этой схемы можно получить, используя условие равенства напряжений на входах ОУ и считая ОУ идеальным. Тогда
,
отсюда коэффициент усиления схемы равен:
.
Повторитель напряжения
Если в неинвертирующем усилителе положить Rвх равным бесконечности (Rвх = ∞), а Rо равным нулю (Rо = 0), то мы придём к схеме, изображённой на рис. 8.11.
Согласно принятым допущениям, напряжение на инвертирующем входе ОУ должно равняться входному напряжению (U вх).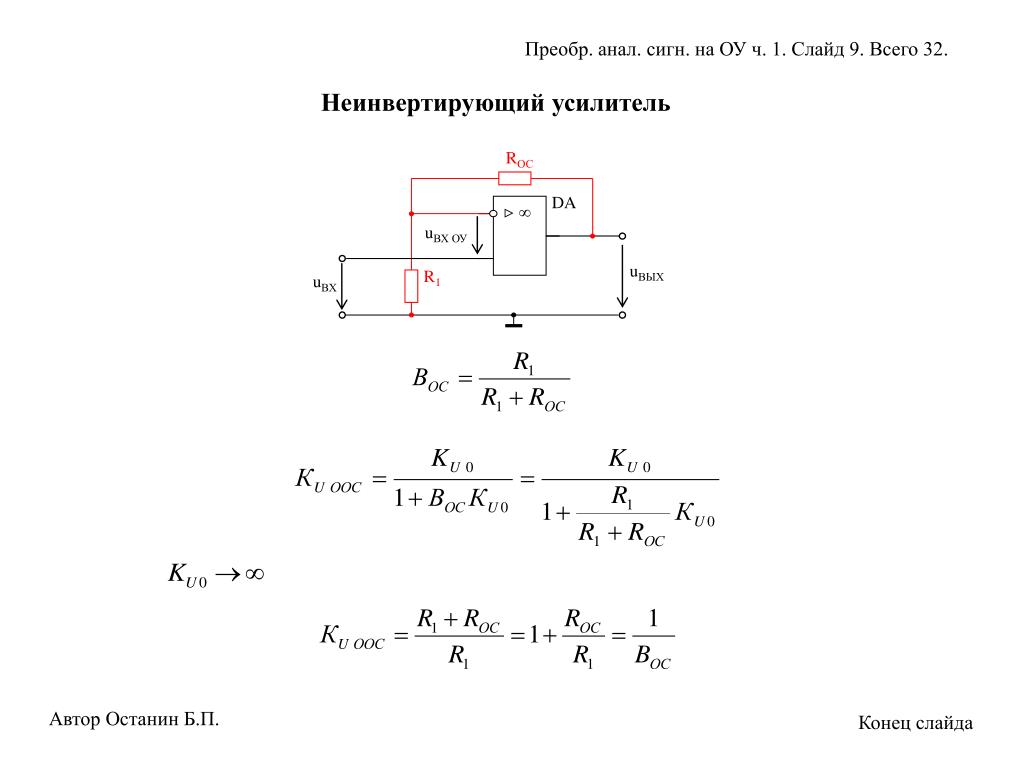
Но, с другой стороны, неинвертирующий вход соединен с выходом схемы. Следовательно, Uвых = Uвх, то есть выходное напряжение повторяет входное напряжение.
Такая схема повторителя напряжения используется в качестве усилителя с большим значением входного сопротивления, обеспечивая развязку предыдущего каскада от нагрузочного влияния следующих за ним каскадов.
Инвертирующий усилитель
В инвертирующем усилителе (рис. 8.12) входной и выходной сигналы сдвинуты по фазе на 180°. Изменение знака выходного сигнала относительно входного создается введением по инвертирующему входу ОУ с помощью резистора Rос параллельной обратной связи по напряжению. Неинвертирующий вход связан с общей точкой (заземляется). Входной сигнал подается через резистор R1 на инвертирующий вход ОУ.
Поэтому Iвх = Uвх / R1. Так как входы ОУ не потрИзмеритель напряжения и коэффициента усиления на усилителе — инструменты электротехники и электроники
Калькулятор напряжения и коэффициента усиления Op-Amp
Калькулятор для вычисления коэффициента усиления и выходного напряжения операционного усилителя
Вывод
V out
(В)
Инвертирование коэффициента усиления
(V out / V 1 )
Получите неинвертирующий
(V out / V 2 )
обзор
Этот калькулятор помогает рассчитать значения выходного напряжения и инвертирующего и неинвертирующего усиления операционного усилителя. Укажите значения резисторов, входных напряжений и напряжения питания и нажмите кнопку «рассчитать».
Операционный усилитель (op-amp) — усилитель напряжения с дифференциальным входом и односторонним выходом. Двумя основными базовыми конфигурациями ОУ являются инвертирующий усилитель и неинвертирующий усилитель.
Термины «инвертирование» и «неинвертирование» относятся к полярности выходного напряжения по отношению к входному напряжению. Инвертирующий усилитель обеспечивает выходное напряжение, которое имеет противоположную полярность по отношению к входному напряжению. Неинвертирующий усилитель не изменяет полярность входного напряжения.
Обратите внимание, что этот калькулятор может использоваться как для инвертирующей, так и для неинвертирующей конфигурации операционного усилителя. Для неинвертирующего операционного усилителя установите V2 на 0V и используйте V1 в качестве входного сигнала. Если требуется инвертирующий операционный усилитель, установите V1 на 0 В и используйте V2 в качестве входа. Используйте очень большое значение для R3 (например, 9999999999), если положительный входной сигнал операционного усилителя должен быть подключен непосредственно к земле.
уравнения
$$ V_ {out} = A V_ {input} $$
Для инвертирования операционного усилителя:
$$ A = — \ frac {R_ {2}} {R_ {1}} $$
Для неинвертирующего операционного усилителя:
$$ A = 1 + \ frac {R_ {2}} {R_ {1}} $$
Приложения
ОУ-усилитель представляет собой модуль дифференциального усилителя с высоким коэффициентом усиления, который формирует центральный компонент во множестве полезных, простых схем усилителя.
Проектирование с помощью операционных усилителей намного проще, чем создание настраиваемых усилителей из дискретных компонентов, а результирующие схемы легко настраиваются в соответствии с потребностями приложения. Основополагающим методом в реализации ОУ является использование отрицательной обратной связи. В типичных инвертирующих и неинвертирующих конфигурациях сеть обратной связи принимает форму двух резисторов. Низкочастотный коэффициент усиления готовой схемы почти полностью определяется значениями этих двух резисторов.
Дальнейшее чтение
- Учебник — Введение в операционные усилители
- Учебник — Инвертирующие и неинвертирующие операционные усилители
- Видео-лекция — характеристики Op-amp
Практическое применение операционных усилителей.Часть первая.
РадиоКот >Статьи >Практическое применение операционных усилителей.Часть первая.
Всем привет.
В этой статье мы обсудим некоторые аспекты практического применения операционных усилителей в повседневной жизни радиолюбителя.
Не растекаясь мыслею по древу и не вдаваясь в дремучие теоретические основы работы вышеозначенного усилителя, давайте все же обозначим некоторые основные термины и понятия, с которыми нам предстоит столкнуться в дальнейшем.
Итак — операционный усилитель. Далее будем называть его ОУ, а то очень лень писать каждый раз полностью.
На принципиальных схемах, чаще всего, он обозначается следующим образом:
На рисунке обозначены три самых главных вывода ОУ — два входа и выход. Разумеется, есть еще выводы питания и иногда выводы частотной коррекции, хотя последнее встречается все реже — у большинства современных ОУ она встроенная.
Два входа ОУ — Инвертирующий и Неинвертирующий названы так по присущим им свойствам. Если подать сигнал на Инвертирующий вход, то на выходе мы получим инвертированный сигнал, то бишь сдвинутый по фазе на 180 градусов — зеркальный; если же подать сигнал на Неинвертирующий вход, то на выходе мы получим фазово не измененный сигнал.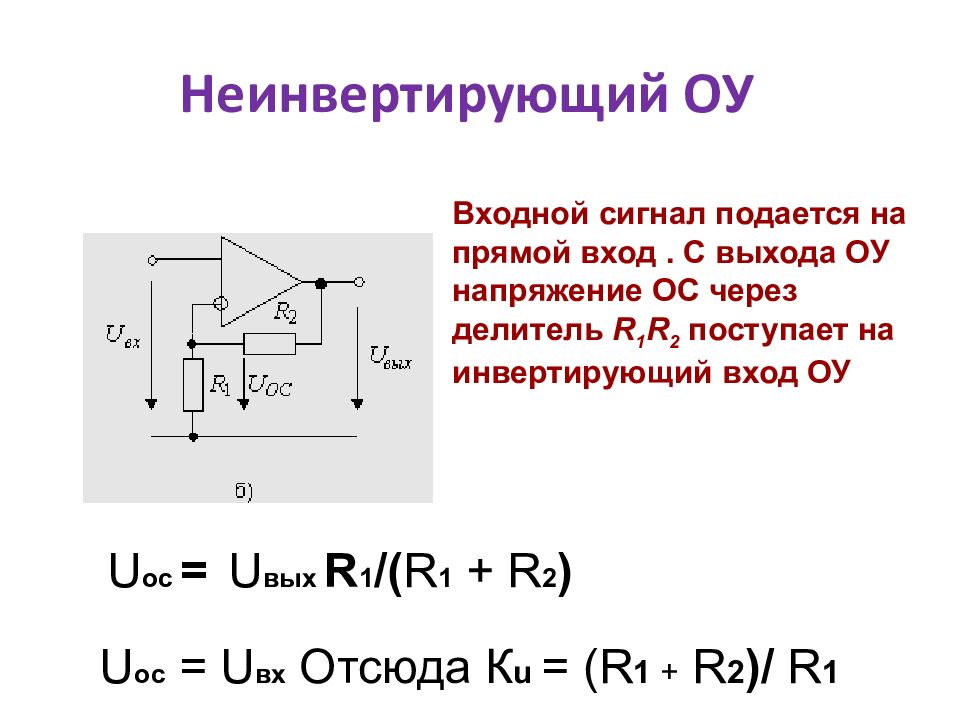
Так же как и основных выводов, основных свойств ОУ тоже три — можно назвать их ТриО (или ООО — кому как нравится): Очень высокое сопротивление входа, Очень высокий коэффициент усиления (10000 и более), Очень низкое сопротивление выхода.
Еще один очень важный параметр ОУ называется скорость нарастания напряжения на выходе (slew rate на буржуинском). Обозначает он фактически быстродействие данного ОУ — как быстро он сможет изменить напряжение на выходе при изменение оного на входе.
Измеряется этот параметр в вольтах в секунду (В/сек).
Этот параметр важен прежде всего для товарищей, конструирующих УЗЧ, поскольку, если ОУ недостаточно быстрый, то он не будет успевать за входным напряжением на высоких частотах и возникнут изрядные нелинейные искажения. У большинства современных ОУ общего назначения скорость нарастания сигнала от 10В/мксек и выше. У быстродействующих ОУ этот параметр может достигать значения 1000В/мксек.
Оценить — подходит ли тот или иной ОУ для ваших целей по скорости нарастания сигнала можно по формуле:
где, fmax — частота синусоидального сигнала, Vmax — скорость нарастания сигнала, Uвых — максимальное выходное напряжение.
Ну да не будем больше тянуть кота за хвост — приступим к главной задаче этого опуса — куда, собственно, эти клевые штуки можно воткнуть и что из этого можно получить.
Первая схема включения ОУ — инвертирующий усилитель.
Наиболее популярная и часто встречающаяся схема усилителя на ОУ. Входной сигнал подается на инвертирующий вход, а неинвертирующий вход подключается к общему проводу.
Коэффициент усиления определяется соотношением резисторов R1 и R2 и считается по формуле:
Почему «минус»? Потому что, как мы помним, в инвертирующем усилителе фаза выходного сигнала «зеркальна» фазе входного.
Входное сопротивление определяется резистором R1. Ежели его сопротивление, например 100кОм, то и входное сопротивление усилителя будет 100кОм.
Следующая схема — инвертирующий усилитель с повышенным входным сопротивлением.
Предыдущая схема всем хороша, за исключением одного нюанса — соотношение входного сопротивления и коэффициента усиления может не подойти для реализации какого-либо специфического проекта.
Ведь что получается — допустим, нам нужен усилитель с К=100. Тогда, исходя из того, что значения резисторов должны быть в разумных пределах берем R2=1Мом, а R1=10кОм. То есть, входное сопротивление усилителя будет равным 10 кОм, что в некоторых случаях недостаточно.
В этих самых случая можно применить следующую схему:
В данном случае, коэффициент усиления считается по следующей формуле:
То есть, при том же коэффициенте усиление сопротивление R1 можно увеличить, а значит и повысить входное сопротивление усилителя.
Едем дальше — неинвертирующий усилитель.
Выглядит он следующим образом:
Коэффициент усиления определяется так:
В данном случае, как видите, никаких минусов нет — фаза сигнала на входе и на выходе совпадает.
Основное отличие от инвертирующего усилителя заключается в повышенном входном сопротивлении, которое может достигать 10Мом и выше.
Если при реализации данной схемы в практических конструкциях, необходимо предусмотреть развязку с предыдущими каскадами по постоянному току — установить разделительный конденсатор, то нужно между входом ОУ и общим проводом включить резистор сопротивлением около 100кОм, как показано на рисунке.
Если этого не сделать, то ОУ перевозбудится и ничего дельного вы от него не получите. Ну кроме половины питания на выходе.
Усилитель с изменяемым коэффициентом усиления.
Примем R1=R2=R3=R. И введем некую переменную А, которая может принимать значения от 1 до 0 в зависимости от поворота движка переменного резистора R3.
Тогда коэффициент усиления можно определить так:
K=2A-1
Входное сопротивление практически не зависит от положения движка переменного резистора.
Так, с усилителями разобрались — дальше у нас по плану — фильтры.
Вопросы, как обычно, складываем тут.
Как вам эта статья? | Заработало ли это устройство у вас? |
Неинвертирующий усилитель — Большая Энциклопедия Нефти и Газа, статья, страница 4
Неинвертирующий усилитель
Cтраница 4
Из формулы (4.7) видно, что входное сопротивление неинвертирующего усилителя довольно большое. [47]
При выполнении условия ro c значение коэффициента усиления неинвертирующего усилителя (10.37) стремится к единице. [48]
При выполнении условия г г значение коэффициента усиления неинвертирующего усилителя (10.37) стремится к единице. [49]
Рассмотрим представленную на рис. 10.42, а схему неинвертирующего усилителя напряжения. [51]
Дифференциальный усилитель может быть и инвертирующим, и неинвертирующим усилителем. Инвертирующий дифференциальный усилитель получается, если вход заземлен, а неинвертирующий дифференциальный усилитель получается, если вход — заземлен. На два входа подаются сигналы, и усилитель усиливает разницу между ними. Причем, если коэффициенты усиления в обеих схемах равны, то результат будет одинаковый. [53]
Радикальное решение этой проблемы заключается в использовании повторителей или неинвертирующих усилителей для получения высокого полного входного сопротивления. [55]
Другой широко распространенный вариант включения ОУ реализуется в виде неинвертирующего усилителя, принципиальная схема которого приведена на рис. 3.47. Входной сигнал здесь поступает на неинвертирующий вход ОУ, а на инвертирующий подается сигнал обратной связи. Нетрудно показать, что в инвертирующем усилителе на ОУ имеет место последовательная ООС по напряжению. [56]
Радикальное решение этой проблемы заключается в использовании повторителя или неинвертирующего усилителя для получения высокого входного полного сопротивления. [57]
В связи с этим выясним, насколько идеальный коэффициент усиления неинвертирующего усилителя, охваченного отрицательной ОС, отличается от реального. [58]
Сравнивая (4.159) с выражением (4.148), нетрудно установить, что коэффициент усиления неинвертирующего усилителя отличается от коэффициента усиления инвертирующего усилителя не только знаком, но и численно даже при идеальных параметрах ОУ. [59]
Схема, показанная на рис. 70, б, предназначена для построения неинвертирующего усилителя с последовательной обратной связью. [60]
Страницы: 1 2 3 4
Рассчитайте коэффициент усиления неинвертирующего усилителя на ОУ, если: Rос=22 кОм; Rз=2,3
знайти потенціал сферичної краплі ртуті, що утворилась від злиття 5 однакових крапель ртуті, кожна з яких мала заряд 1 нКл і радіус r = 1 мм
Через який час t* від початку руху точка, що здійснює коливання за рівнянням х(t) = 7 cos 0,5пt, пройде шлях від стану рівноваги до максимального зміщ … ення?
Помогите решить задачу по магнетизму! Перпендикулярно к однородному электрическому полю напряженностью 80000 В/м, возбуждено однородное магнитное поле … напряженностью 4000 А/м. Пучок электронов, движущихся перпендикулярно к линиям напряженности того и другого поля, не испытывает отклонения. Найти скорость электронов. Правильный ответ= 16 Мм/с
Заряженная частица после прохождения разности потенциалов 1кВ приобретает энергию 8000кВ.Определить заряд частицы ,выразив его через заряд.
В двух вершинах одностороннего треугольника со стороной 0,5м находятся точечные заряды 3 и — 2 мк Кл.Найти потенциал электрического поля в третьей вер … шине.
соч срочно 30балов
ФІЗІКАААААААААААААААА
1.Чан высотой 50 см полностью заполнен подсолнечным маслом.Рассчитайте давление на глубине 18 см ниже верхнего уровня масла. 2.Давление,оказываемое жи … дкостью на дно,равно 1775 Па.Какая это житкость,если высота её столба 25 см? 3.Какую жидкость залили в контейнер,если её уровень 3,8 м,а давление на дно 30020 Па? 4.В сосуд налили ртуть на высоту 6 см,затем долили воду до общего уровня 20см.А когда сверху долили слой нефти,давление на дно оказалось равным 12кПа.Каково общее давление воды и нефти на ртуть? 5.С какой силой вода давит на плотину,если высота плотины до уровня воды 15 см,а ширина 200м? 6.В сосуд налиты ртуть,вода и керосин.Слой каждой жидкости имеет толщину 10см.Определите давление и силу,с которой жидкость действует на кран площадью 4 см2,находящийся на высоте 5 см от дна сосуда. Пожалуйста решите это всё!!!
Rак зависит освещённость от вида осветителя ?
За допомогою похилої площини довжиною 8 м піднімають вантаж масою 60 кг на висоту 1,6 м. Яку при цьому силу у Н застосовують? Тертям знехтуйте.
Буферный и неинвертирующий операционный усилитель
Буферный усилитель с единичным усилением реализован с использованием операционного усилителя в конфигурации с отрицательной обратной связью. Выход подключен к своему инвертирующему входу, а источник сигнала подключен к неинвертирующему входу. Хотя его коэффициент усиления по напряжению равен 1 или единице, он имеет высокое усиление по току, высокое входное сопротивление и низкое выходное сопротивление. Он используется, чтобы избежать загрузки источника сигнала.
Выходное напряжение операционного усилителя определяется уравнением: \ begin {уравнение} V_ {out} = {A_ {OL} \, (V _ {\! +} — V _ {\! -})} \ end {уравнение} где V + — напряжение на неинвертирующем выводе, V− — напряжение на инвертирующем выводе, а A OL — коэффициент усиления без обратной связи усилителя.
Переставьте уравнение \ begin {уравнение} {V_ {out} \ over A_ {OL}} = V _ {\! +} — V _ {\! -} \ end {уравнение}
Если предположить, что A OL равно ∞, \ begin {уравнение} V_- = V_ + \ end {уравнение} Только для схем операционных усилителей с отрицательной обратной связью мы используем уравнение 3, чтобы упростить анализ схем.
Для этого буферного усилителя, используя уравнение 3, при осмотре можно получить \ begin {уравнение} V_ {выход} = V_- = V_ + = V_ {дюйм} \ end {уравнение} и получить коэффициент усиления буферного усилителя операционного усилителя \ begin {уравнение} V_ {out} = V_ {in} \ end {уравнение}
Неинвертирующий операционный усилитель обеспечивает усиление по напряжению.Буферный усилитель можно рассматривать как частный случай этого усилителя с Rf = 0 и Rg = ∞.
Если мы позволим входному току на инвертирующий вход I- = 0 и подадим KVL на петли Vout, Rf и Rg \ begin {уравнение} V_- = {V_ {out}} {{R_g} \ over {R_f + R_g}} \ end {уравнение} Применяя уравнение 3, \ begin {уравнение} V_ {in} = V_ + = V_- = {V_ {out}} {{R_g} \ over {R_f + R_g}} \ end {уравнение} Измените уравнение, чтобы получить коэффициент усиления неинвертирующего усилителя операционного усилителя. \ begin {уравнение} V_ {out} = (1 + {{R_f} \ over {R_g}}) {V_ {in}} \ end {уравнение}
Поскольку доходы от рекламы падают, несмотря на рост числа посетителей, нам нужна ваша помощь в поддержании и улучшении этого сайта, что требует времени, денег и тяжелого труда.Благодаря щедрости наших посетителей, которые давали ранее, вы можете использовать этот сайт бесплатно.
Если вы получили пользу от этого сайта и можете, пожалуйста, отдать 10 долларов через Paypal . Это позволит нам продолжаем в будущее. Это займет всего минуту. Спасибо!
Я хочу дать!
© 2021 Emant Pte Ltd Co., рег. № 200210155R | Условия использования | Конфиденциальность | О нас
Операционный неинвертирующий усилитель | Книга Ultimate Electronics
Ultimate Electronics: практическое проектирование и анализ схем
Схема операционного усилителя, образующая усилитель напряжения, использующая отрицательную обратную связь для умножения входного сигнала на положительный коэффициент усиления, установленный двумя резисторами.Читать 16 мин
В предыдущих разделах мы показали, что, добавив один провод к идеальному операционному усилителю, мы можем создать буфер напряжения операционного усилителя с коэффициентом усиления 1, используя обратную связь с обратной связью. В этом разделе мы покажем, как можно добавить два резистора, чтобы создать неинвертирующий усилитель , и выбрать желаемый уровень усиления по напряжению, усиливая сигнал напряжения на Av≥1. .
В частности, мы можем подключить резистивный делитель напряжения к выходу операционного усилителя, а затем подключить средний вывод этого делителя напряжения обратно к инвертирующему входу операционного усилителя:
Как обсуждалось в разделе «Делители напряжения», резисторы R1 и R2 образуют промежуточную точку напряжения, которая пропорциональна выходному сигналу, но масштабируется на меньше на коэффициент, определяемый номиналами резисторов.
Это промежуточное напряжение Vdiv затем подключается через провод обратно к инвертирующему (-) входу операционного усилителя.
Концептуально операционный усилитель регулирует выходное напряжение до тех пор, пока два его входа не станут равными. Единственный способ уравнять два входа операционного усилителя — это пропорционально масштабировать выход на больше таким образом, чтобы нивелировать масштабирование делителя напряжения с понижением.
R1 и R2 образуют делитель напряжения, который, как мы можем предположить, не нагружен, поскольку операционный усилитель имеет нулевой входной ток.Это дает нам одно уравнение:
Vdiv = (R2R1 + R2) Vout = fVout
где f = R2R1 + R2 — доля делителя напряжения.
Для удобства, давайте определим обратную долю делителя напряжения как наше расчетное усиление k :
к = 1f = R1 + R2R2
Идеальный операционный усилитель изменяет свой выход до тех пор, пока два входа не станут равными. Когда все работает нормально, дает нам уравнение:
Вин = Vdiv
Мы можем объединить эти два уравнения, чтобы найти связь между вводом и выводом:
Вин = fVoutVout = 1fVinAv = VoutVin = 1f = k
Поскольку делитель напряжения может выдавать только дробь 0≤f≤1 , сигнал усиливается на коэффициент усиления по напряжению:
Av = 1f = k≥1
Мы можем смоделировать операционный усилитель как источник напряжения, управляемый напряжением (VCVS), как мы это делали в предыдущих разделах по операционным усилителям, чтобы мы могли провести более подробный анализ:
VCVS дает нам одно уравнение:
Vout = AOL (Vin − Vdiv)
Делитель напряжения продолжает быть разгруженным, поэтому мы все еще можем подставить в наш делитель напряжения дробь Vdiv = fVout и упростить:
Vout = AOL (Vin − fVout) Vout = AOLVin − AOLfVoutVout (1 + AOLf) = AOLVinVoutVin = AOL1 + AOLf
Для идеального операционного усилителя возьмем предел AOL → ∞ , производя списание в числителе и знаменателе:
Av = VoutVin≈1f = k
Опять же, поскольку 0≤f≤1 , поэтому k≥1 , поэтому эта схема дает усиление Av≥1 .
Мы можем сделать усилитель с коэффициентом усиления 10, установив делитель напряжения на долю f = 110 . Например:
Exercise Щелкните, чтобы открыть и смоделировать схему выше. Какая амплитуда выходного сигнала по сравнению с входным? Можете ли вы изменить R1, чтобы вместо этого усилитель имел коэффициент усиления 20?
Концептуально представьте, что мы начинаем со всех напряжений, равных нулю. Затем внезапно мы меняем вход на 1 вольт. Операционный усилитель видит большую разницу между своим неинвертирующим (+) входом при 1 В и инвертирующим (-) выходом при 0 В, поэтому (как обсуждалось в разделе об идеальном операционном усилителе) выходной сигнал начинает расти.Когда выход достигает 1 В, инвертирующий выход по-прежнему видит только 0,1 В, поэтому выход продолжает расти. Только когда выходное напряжение возрастает до 10 вольт, делитель напряжения выдает 1 вольт на инвертирующем входе, останавливая дальнейшее повышение выходного напряжения.
Мы действительно можем изучить это, посмотрев на шаговый отклик :
Exercise Щелкните, чтобы открыть и смоделировать схему выше. Какая кривая соответствует неинвертирующему входу операционного усилителя? Что соответствует инвертирующему входу? Что произойдет, если вы увеличите усиление до 100 и повторно запустите симуляцию? (Подсказка: возможно, вам придется изменить время остановки симуляции!)
Чтобы выявить это во времени, мы использовали операционный усилитель с конечным произведением коэффициента усиления и полосы пропускания GBW = 1 ГГц. .(Поистине идеальный операционный усилитель имел бы GBW = ∞ .) Результат показывает, что операционному усилителю требуется несколько наносекунд, чтобы «замкнуть контур» и уравновесить два своих входа.
В предыдущих разделах мы говорили о реальных операционных усилителях, имеющих конечное произведение коэффициента усиления и полосы пропускания (GBW). На тот момент было не совсем понятно, зачем мы умножаем (произведение) безразмерное усиление (усиление) на полосу пропускания (в Гц), но неинвертирующий усилитель прояснит это.
Это легче всего увидеть на примере моделирования, в котором мы берем операционный усилитель с GBW = 1 МГц. и настроить его как неинвертирующий усилитель с различными уровнями усиления:
Exercise Щелкните, чтобы открыть и смоделировать схему выше.Мы попросили симулятор повторно запустить эту схему для DC_GAIN = 1, 10, 100, 1000, 10000 и 100000. По мере того, как мы увеличиваем коэффициент усиления каждый раз в 10 раз (нанесено на логарифмическую шкалу децибел y- оси, поэтому они нанесены равномерно с интервалом +20 дБ шагов), что происходит с −3 дБ угловая частота отклика усилителя?
Эта симуляция показывает, что чем больше мы просим усилитель, тем медленнее становится!
Вы можете подтвердить это, запустив моделирование во временной области и посмотрев, сколько времени требуется, чтобы выходной сигнал установился в пределах, скажем, 5% от его окончательного значения.Вы увидите, что каждый раз, когда мы проектируем схему с 10-кратным усилением, на расчет также уходит в 10 раз больше времени.
Это происходит потому, что коэффициент усиления нашего операционного усилителя не соответствует AOL на высоких частотах; он уменьшается на более высоких частотах. Как было показано ранее, передаточная функция Лапласа для идеального операционного усилителя без обратной связи составляет:
G (s) = AOL1 + s (AOL2πGBW)
Это выражение включает коэффициент усиления без обратной связи AOL. который охватывает постоянный ток и низкие частоты, и он падает после произведения коэффициента усиления на полосу пропускания GBW .Мы можем заменить это на нашу модель неинвертирующего усилителя, вставив G (s) вместо AOL только для DC :
VoutVin (s) = G (s) 1 + G (s) fVoutVin (s) = AOL1 + s (AOL2πGBW) 1 + fAOL1 + s (AOL2πGBW) VoutVin (s) = AOL1 + s (AOL2πGBW) + fAOLVoutVin (s ) = 1 (f + 1AOL) + s (12πGBW)
Это говорит нам о сложной частотной характеристике неинвертирующего усилителя для синусоидального сигнала на входе с частотой s = jω = j2πfs. .
(обратите внимание на возможную путаницу: мы используем f для обозначения доли безразмерного делителя напряжения, а fs для обозначения частоты сигнала в Гц.)
Если мы посмотрим на это выражение только на DC, то s = 0 итак:
VoutVin (s = 0) = 1f + 1AOL (при постоянном токе)
Если умножить числитель и знаменатель на AOL вы увидите, что это идентично AOL1 + fAOL выражение, которое мы нашли ранее в этом разделе. И аналогично, поскольку 1AOL≪f , мы можем игнорировать 1AOL срок. (Обратите внимание, что если мы попытаемся использовать делитель напряжения, чтобы выбрать коэффициент усиления с обратной связью, который аналогичен или больше, чем коэффициент усиления разомкнутого цикла операционного усилителя, то это приближение не будет выполняться, и усилитель не будет работать так, как вы предназначено, даже в DC.)
Давайте воспользуемся этим упрощением, чтобы заменить (f + 1AOL) ≈f в знаменателе и поместите это обратно в наше предыдущее выражение:
VoutVin (s) = 1f + s (12πGBW)
А теперь вместо ссылки на делитель напряжения дробь 0≤f≤1 , обратимся к нему, расчетный коэффициент усиления напряжения k = 1f . Умножение числителя и знаменателя на k :
VoutVin (s) = k1 + s (k2πGBW)
Эту передаточную функцию с обратной связью можно разложить на произведение коэффициента усиления k и однополюсный фильтр нижних частот 11 + s (k2πGBW) .
Мы можем найти угловую частоту фильтра нижних частот, определив, где мнимая часть знаменателя равна по величине действительной части:
| 1 | = | s (k2πGBW) || 1 | = | jωc (k2πGBW) | 1 = ωc (k2πGBW) 1 = 2πfc (k2πGBW) 1 = fc (kGBW) fc = GBWk
Это последнее уравнение говорит нам, что угловая частота замкнутого контура усилителя fc равно произведению коэффициента усиления и ширины полосы частот, деленному на коэффициент усиления:
- Если коэффициент усиления k = 10 и GBW = 106 Гц , то fc = 106 Гц10 = 105 Гц .
- Если коэффициент усиления k = 100 и GBW = 106 Гц , то fc = 106 Гц 100 = 104 Гц .
- Если коэффициент усиления k = 1000 и GBW = 106 Гц , то fc = 106 Гц 1000 = 103 Гц .
Для данного операционного усилителя (то есть с фиксированным произведением коэффициента усиления и полосы пропускания) угловая частота замкнутого контура становится ниже, когда вы просите его сделать большее усиление. Существует прямой компромисс между характеристиками усилителя с точки зрения усиления и характеристиками с точки зрения полосы пропускания.
Это не чисто теоретическое.Вы, вероятно, столкнетесь с этой проблемой при разработке реальных операционных усилителей! Например, если вам нужно усиление 1000, и вам одновременно нужно обрабатывать сигналы 105 Гц , у вас есть несколько вариантов:
- Используйте более быстрый операционный усилитель. Купите операционный усилитель с более высоким значением GBW.
- Разделите общий выигрыш на несколько этапов. Используйте два или три более медленных операционных усилителя, возможно, с усилением только 10 за раз, что позволит вам получить более высокие частоты излома на каждом этапе.
Ограниченная частотная характеристика также проявляется в более медленной переходной характеристике во временной области. Смоделируйте схему выше и посмотрите, сколько времени потребуется, чтобы прийти к окончательному значению после шага ввода для различных конфигураций усиления.
Обратите внимание, что делитель напряжения уменьшает выходной сигнал на на некоторую долю 0≤f≤1 , в то время как общий эффект замкнутой цепи фактически делает выход больше , чем вход на k = 1f≥1 .
На самом деле это простой случай распространенной, но сбивающей с толку концепции в системах обратной связи: изменение пути обратной связи (например, умножение на f ) обычно вызывает обратный или обратный эффект (например, умножение на 1f ) ко всей системе после применения обратной связи с обратной связью. Это важная идея, и ее трудно понять в целом, но неинвертирующий усилитель иллюстрирует концепцию самым простым из возможных способов.
Для читателей, знакомых с передаточными функциями: это эквивалентно тому, что передаточная функция с обратной связью попадает в знаменатель ответа замкнутого контура.
В общем, мы можем взглянуть на систему обратной связи с передаточной функцией G и передаточная функция обратной связи H как изображено здесь:
Для простоты рассмотрим эти множители G и H быть константами, выполняя мультипликативное масштабирование их ввода.
Наша блок-схема имеет четыре помеченных узла для условий ввода, вывода, ошибки и обратной связи.
Три элемента блок-схемы (одно вычитание и два умножения передаточной функции) позволяют построить систему из трех уравнений:
Verr = Vin − VfbVfb = H⋅VoutVout = G⋅Verr
Мы хотели бы найти замкнутую связь между вводом и выводом без Verr или Vfb термины.Мы можем объединить приведенные выше уравнения, подставив Vfb и Верр найти:
Vout = G⋅ (Vin − H⋅Vout) Vout = G⋅Vin − GH⋅VoutVout (1 + GH) = G⋅VinVoutVin = G1 + GH
Это последнее уравнение представляет собой передаточную функцию замкнутого контура , и оно связывает вход с выходом после рассмотрения эффектов контура обратной связи. Это очень полезный общий результат!
Особенно интересным случаем является рассмотрение того, что происходит, когда | GH | ≫1 . В этом случае мы можем аппроксимировать, что 1 + GH≈GH в знаменателе, и в этом случае уравнение упрощается:
VoutVin≈GGH = 1H (если | GH | ≫1)
Это замечательный результат: если величина усиления контура | GH | велико по сравнению с 1, то передаточная функция G фактически отменяет результат замкнутого контура, и ответ замкнутого контура определяется только обратной величиной передаточной функции обратной связи, 1H .
В случае неинвертирующего усилителя на операционном усилителе на постоянном токе передаточная функция G = AOL , усиление разомкнутого контура операционного усилителя. Передаточная функция обратной связи H = f , доля делителя напряжения, так как только часть выходного сигнала возвращается на вход.
Начиная с типичных значений для AOL≫100000 и дробь 0≤f≤1 , произведение | GH | = | fAOL | ≫1 для всех, кроме очень маленьких значений f . (Мы проигнорируем этот диапазон очень малых f значений, поскольку они представляют собой условие, при котором мы пытаемся разработать неинвертирующий усилитель с усилением замкнутого контура больше, чем усиление разомкнутого контура усилителя, что не будет работать!) Таким образом, усиление замкнутого контура равно всего:
VoutVin≈1f = k
Когда мы заботимся об отклике систем с частотно-зависимым поведением, например, когда мы анализировали вышеупомянутый компромисс между коэффициентом усиления и шириной полосы, мы все равно можем применить область Лапласа к тому же общему результату с обратной связью:
Vout (s) Vin (s) = G (s) 1 + G (s) H (s)
До сих пор мы рассматривали только соотношение и номиналов резисторов в нашем резистивном делителе, поскольку это то, что определяет наше усиление.(Мы даже можем использовать потенциометр, чтобы сделать усилитель с регулируемым усилением.)
Но как нам выбрать абсолютные значения резистора ? Если мы хотим разработать усилитель с коэффициентом усиления Av = 10 , почему мы должны выбрать (R1 = 90 кОм, R2 = 10 кОм) вместо (R1 = 9 Ом, R2 = 1 Ом) , хотя оба производят одинаковый коэффициент делителя напряжения?
Ответы аналогичны компромиссам, обсуждаемым в разделе «Делители напряжения». С обеих сторон есть опасения и недостатки:
Если сопротивление слишком мало:
- Чрезмерное потребление энергии. Рассеивание мощности на резисторах становится значительным, что может привести к перегреву резисторов или даже самого операционного усилителя.
- Выходное сопротивление и пределы питающей шины. Настоящие операционные усилители имеют ненулевое выходное сопротивление. Их способность управлять большими токами особенно ограничена рядом с шинами питания. Вы можете обнаружить, что выходной диапазон скомпрометирован при использовании слишком маленьких резисторов.
Вот симуляция, показывающая последнюю проблему:
Exercise Щелкните, чтобы открыть и смоделировать схему выше.Синусоидальная волна амплитудой 1 В усиливается на k = 10 , который должен соответствовать шинам питания 10 В. Однако этот операционный усилитель имеет выходное сопротивление RO = 10 Ом. , что ограничивает его способность управлять выходом вблизи рельсов. Как выглядит результирующий сигнал? Что произойдет, если вы измените R1 и R2, чтобы они были в 2 раза меньше или больше?
Обратите внимание, что эта проблема усугубляется еще больше, если выход операционного усилителя загружен. В качестве упражнения добавьте сопротивление нагрузки к выходу и посмотрите, как изменится сигнал.
Эти проблемы вызывают нелинейное ограничение , которое разрушает информацию и вызывает искажения для всех последующих каскадов сигнала.
Если сопротивление слишком велико:
- Чрезмерный шум. Шум напряжения резистора увеличивается с увеличением сопротивления.
- Ошибка нагрузки из-за входного тока операционного усилителя. В то время как идеальный операционный усилитель имеет нулевой входной ток, реальные операционные усилители обычно имеют небольшой ток на входах. Если резисторы делителя напряжения слишком большие, это может вызвать нежелательное падение напряжения, что приведет к нежелательному смещению.
- Проблемы со стабильностью. Паразитные емкости оказывают большее влияние на узлы с высоким импедансом. При обратной связи с высоким коэффициентом усиления это становится особенно опасным. Обсудим это дальше.
В типовой конструкции обычно выбираются значения в диапазоне:
1 кОм≤ (R1 + R2) ≤1 МОм
Это уже очень широкий диапазон, поэтому не удивляйтесь, если вы увидите некоторые конструкции операционных усилителей за его пределами, но вам следует дважды проверить, могут ли они быть подвержены одной или нескольким из вышеперечисленных проблем.
Что произойдет, если возникнет непреднамеренная, но неизбежная паразитная емкость в цепи обратной связи? Давайте смоделируем это как конденсатор между инвертирующим входом и землей. Концептуально мы можем проследить идеальный операционный усилитель, увеличивая или уменьшая его выходную мощность в зависимости от непосредственной разницы на входах:
- Вход скачка напряжения на неинвертирующем выводе заставляет выход операционного усилителя начинать повышаться и повышаться.
- При нарастании выхода начинает пропускаться ток через делитель напряжения.Но из-за емкости нарастающий выходной сигнал не сразу распространяется обратно на инвертирующий вход.
- Конденсатору требуется время для зарядки, и он может заряжаться только через резисторы. На это нужно время.
- В результате выход операционного усилителя продолжает расти и расти. Если емкость достаточно велика, выходной сигнал операционного усилителя продолжает расти, намного превышая точку, в которой он должен стабилизироваться, потому что конденсатор все еще заряжается. Это называется превышением .
- В конце концов, конденсатор заряжается до точки, в которой он соответствует и даже превышает неинвертирующее входное напряжение.В этот момент операционный усилитель начинает уменьшать свою выходную мощность.
- Однако, поскольку выходная мощность все еще выше точки установившегося состояния, конденсатор все еще заряжается, все выше и выше, вызывая дальнейший выброс!
- В конце концов, мощность на выходе падает настолько, что конденсатор начинает разряжаться.
- Колебания (также называемые звонком ) в конечном итоге стабилизируются до точки установившегося состояния, когда конденсатор не заряжается и не разряжается выходом.
Фактически у нас есть две медленные вещи, преследующие друг друга:
- Операционный усилитель и его произведение с ограниченным коэффициентом усиления и полосы пропускания, и
- RC-цепь, образованная делителем напряжения плюс емкость.
В этом моделировании вы можете видеть, что, когда паразитная емкость C1 достаточно велика, напряжение конденсатора продолжает расти намного выше предполагаемого значения, не совпадая по фазе с пиком выходного напряжения:
Exercise Щелкните, чтобы открыть и смоделировать схему выше.Как паразитная емкость в несколько пикофарад влияет на переходную характеристику?
В качестве упражнения попробуйте сделать R1 и R2 в 10 раз больше. Что происходит?
Что-нибудь изменится, если C1 подключен между двумя входами операционного усилителя, а не между инвертирующим входом и землей? Почему или почему нет?
Паразитная емкость — реальная проблема высокоскоростных усилителей, и проблемы со стабильностью контура обратной связи — одна из них. Мы называем это стабильностью , потому что в крайних случаях это может стать нестабильным и постоянно колебаться, никогда не достигая окончательного значения.(Вы можете приблизиться к этому в симуляторе, сделав C1 очень большим. В симуляторе он в конечном итоге стабилизируется, но в реальном мире он может фактически постоянно колебаться из-за дополнительной задержки, вызванной скоростью света, если ничего другого!)
Есть несколько способов решить эту проблему:
- Составьте физическую схему для уменьшения паразитной емкости.
- Используйте меньшие сопротивления.
- Используйте более медленный операционный усилитель (более низкий GBW) и принимайте более медленные ответы в обмен на стабильность.
- Добавьте компенсационный конденсатор с прямой связью, как мы покажем далее.
Последний вариант решения нашей проблемы со стабильностью стоит кратко продемонстрировать. Мы можем добавить небольшой компенсационный конденсатор C2 с прямой связью параллельно с R1.
(Помните, что C1 — это не конденсаторный компонент, который мы покупаем и устанавливаем в нашу схему, а вместо этого просто паразитная емкость, которая возникает из схемы схемы. Напротив, C2 — это специально добавленный конденсатор, хотя паразитные свойства могут способствовать этому. также.)
Этот дополнительный конденсатор действительно помогает, потому что он помогает подтолкнуть увеличение выходного напряжения непосредственно с выхода к паразитной емкости C1, без задержки ожидания заряда C1 через R1.
Выбор значения для C2 сложен и включает в себя расчетное усиление усилителя, произведение коэффициента усиления операционного усилителя на ширину полосы, задействованные сопротивления и значение паразитной емкости. Тем не менее, можно выбрать путем моделирования или экспериментов.Вот пример, в котором мы тестируем различные номиналы компенсационного конденсатора:
Exercise Щелкните, чтобы открыть и смоделировать схему выше. Какую емкость лучше всего выбрать для C2 в этой ситуации?
- Если компенсационная емкость слишком мала (или равна нулю), мы будем иметь нестабильность и перерегулирование в переходной характеристике.
- Если компенсационная емкость слишком высока, она слишком сильно замедлит переходную характеристику усилителя.
- Но есть зона Златовласки посередине (около 5-6 пФ в этом примере), где ступенчатая характеристика очень хорошая, несмотря на большую паразитную емкость.
Добавление компенсационных конденсаторов — это более продвинутая часть аналоговой магии, но с пониманием того, почему возникают проблемы со стабильностью и как они могут быть исправлены, вы можете использовать моделирование и эксперименты, чтобы решить их, когда они возникнут.
Как вы, возможно, догадались по названию «неинвертирующий», существует также конфигурация инвертирующего усилителя операционного усилителя, которую мы рассмотрим далее.
Роббинс, Майкл Ф. Ultimate Electronics: Практическое проектирование и анализ схем. CircuitLab, Inc., 2021, ultimateelectronicsbook.com. Доступно. (Авторское право © CircuitLab, Inc., 2021)
4.2: Инвертирующие и неинвертирующие усилители
Как отмечалось в нашей предыдущей работе, отрицательная обратная связь может применяться одним из четырех способов. Форма параллельного ввода инвертирует входной сигнал, а форма последовательного ввода — нет. Поскольку эти формы были представлены как измерения тока и напряжения соответственно, у вас может сложиться первоначальное впечатление, что все усилители напряжения должны быть неинвертирующими.Это не тот случай. Например, простым включением одного или двух резисторов можно сделать инвертирующие усилители напряжения или неинвертирующие усилители тока. Реализуемы практически все топологии. Сначала рассмотрим формы источников управляемого напряжения (использующие отрицательную обратную связь SP и PP).
Для анализа вы можете использовать классическое лечение, данное в третьей главе; однако из-за некоторых довольно хороших характеристик типичного операционного усилителя будут показаны приблизительные значения. Эти приближения действительны только в средней полосе и ничего не говорят о высокочастотных характеристиках схемы.Поэтому они не подходят для дискретной работы общего назначения. Идеализации для приближений:
- Входной ток практически равен нулю (т.е. \ (Z_ {in} \) бесконечно).
- Разность потенциалов между инвертирующим и неинвертирующим входами практически равна нулю (т. Е. Коэффициент усиления контура бесконечен). Этот сигнал также называют сигналом ошибки.
Также обратите внимание для ясности, что соединения блока питания не показаны на большинстве схем.
4.2.1: Неинвертирующий усилитель напряжения
Неинвертирующий усилитель напряжения основан на отрицательной обратной связи SP. Пример приведен на рисунке \ (\ PageIndex {1} \). Обратите внимание на сходство с типичными схемами SP из главы 3. Вспоминая основное действие отрицательной обратной связи SP, мы ожидаем очень высокого \ (Z_ {in} \), очень низкого \ (Z_ {out} \) и уменьшения усиления по напряжению. Идеализация 1 утверждает, что \ (Z_ {in} \) должно быть бесконечным. Мы уже знаем, что у операционных усилителей низкий уровень \ (Z_ {out} \), о втором пункте позаботились.Теперь посмотрим на коэффициент усиления по напряжению.
\ [A_ {v} = \ frac {V_ {out}} {V_ {in}} \ notag \]
Потому что в идеале \ (V_ {error} = 0 \)
\ [V_ {in} = V_ {Ri} \ notag \]
Также,
\ [V_ {out} = V_ {Ri} + V_ {Rf} \ notag \]
\ [A_v = \ frac {V_ {Ri} + V_ {Rf}} {V_ {Ri}} \ notag \]
Рисунок \ (\ PageIndex {1} \): Неинвертирующий усилитель напряжения.
Расширение дает
\ [A_v = \ frac {R_i I_ {Ri} + R_f I_ {Rf}} {Ri I_ {Ri}} \ notag \]
Поскольку \ (I_ {in} = 0 \), \ (I_ {Rf} = I_ {Ri} \), и, наконец, мы приходим к
\ [A_v = \ frac {R_i + R_f} {R_i} \ text {или} \ notag \]
\ [A_v = 1+ \ frac {R_f} {R_i} \ label {4.1} \]
Вот это удобно. Коэффициент усиления этого усилителя задается соотношением двух резисторов. Чем больше \ (R_f \) относительно \ (R_i \), тем больше вы получите. Помните, это приблизительное значение. Усиление замкнутого контура никогда не может превышать усиление разомкнутого контура, и в конечном итоге \ (A_v \) будет падать с увеличением частоты. Обратите внимание, что расчет игнорирует влияние импеданса нагрузки. Очевидно, что если \ (R_l \) слишком мало, чрезмерное потребление тока приведет к обрезанию ОУ.
Пример \ (\ PageIndex {1} \)
Каковы входное сопротивление и коэффициент усиления схемы на рисунке \ (\ PageIndex {2} \)?
Во-первых, \ (Z_ {in} \) в идеале бесконечно.Теперь о приросте:
\ [A_v = 1+ \ frac {R_f} {R_i} \ notag \]
\ [A_v = 1+ \ frac {10 k} {1 k} \ notag \]
\ [A_v = 11 \ notag \]
Рисунок \ (\ PageIndex {2} \): неинвертирующая схема для примера \ (\ PageIndex {1} \).
Обратный процесс разработки усилителя столь же прост.
Пример \ (\ PageIndex {2} \)
Разработайте усилитель с коэффициентом усиления 26 дБ и входным сопротивлением 47 кОм (\ Omega \). Для усиления сначала превратите 26 дБ в обычную форму.Это коэффициент усиления по напряжению около 20.
\ [A_v = 1+ \ frac {R_f} {R_i} \ notag \]
\ [\ frac {R_f} {R_i} = A_v — 1 \ notag \]
\ [\ frac {R_f} {R_i} = 19 \ notag \]
Рисунок \ (\ PageIndex {3} \): неинвертирующий дизайн для примера \ (\ PageIndex {2} \).
На этом этапе выберите значение для одного из резисторов и решите для другого. Например, все будет действительным:
\ [R_i = 1k \ Omega, \ R_f = 19k \ Omega \]
\ [R_i = 2 k \ Omega, \ R_f = 38 k \ Omega \]
\ [R_i = 500 \ Omega, \ R_f = 9.5 к \ Омега \]
Однако большинство из них не являются стандартными значениями и потребуют небольших корректировок для производственной схемы (см. Приложение B). Разумный диапазон: \ (100 k \ Omega> R_i + R_f> 10 k \ Omega \). Точность этого усиления будет зависеть от точности резисторов. Теперь о требовании \ (Z_ {in} \). Это обманчиво просто. Предполагается, что \ (Z_ {in} \) бесконечно, поэтому все, что вам нужно сделать, это разместить 47 k \ (\ Omega \) параллельно входу. Полученная схема показана на рисунке \ (\ PageIndex {3} \).
Если конкретный \ (Z_ {in} \) не указан, параллельный входной резистор не требуется. Есть одно исключение из этого правила. Если источник возбуждения не соединен напрямую со входом операционного усилителя (например, он имеет емкостную связь), потребуется резистор для установления обратного пути постоянного тока на землю. Без обратного пути постоянного тока каскад дифференциального усилителя входной секции не будет смещен должным образом. Этот момент стоит запомнить, так как он может значительно избавить вас от головной боли в будущем. Например, в лаборатории схема, подобная показанной на рисунке \ (\ PageIndex {2} \), может нормально работать с одним генератором функций, но не с другим.Это было бы так, если бы второй генератор использовал выходной конденсатор связи, а первый — нет.
Пример \ (\ PageIndex {3} \)
Разработайте повторитель напряжения (т.е. в идеале бесконечный \ (Z_ {in} \) и коэффициент усиления по напряжению 1).
Часть \ (Z_ {in} \) достаточно проста. Что касается второй части, какое отношение \ (R_f \) к \ (R_i \) даст прирост 1?
\ [A_v = 1+ \ frac {R_f} {R_i} \ notag \]
\ [\ frac {R_f} {R_i} = A_v — 1 \ notag \]
\ [\ frac {R_f} {R_i} = 0 \ notag \]
Рисунок \ (\ PageIndex {4} \): повторитель напряжения для примера \ (\ PageIndex {3} \).
Здесь сказано, что \ (R_f \) должно быть 0 \ (\ Omega \). На практике это означает, что \ (R_f \) заменяется перемычкой. А что насчет \ (R_i \)? Теоретически подойдет практически любое значение. Пока есть выбор, считайте бесконечным. Ноль деленный на бесконечность, безусловно, равен нулю. Практическая выгода от выбора \ (R_i = \ infty \) заключается в том, что вы можете удалить \ (R_i \). Полученная схема показана на рисунке \ (\ PageIndex {4} \). Помните, что если источник не подключен напрямую, потребуется резистор возврата постоянного тока.Значение этого резистора должно быть достаточно большим, чтобы избежать нагрузки на источник.
Как видите, проектирование с операционными усилителями может быть намного быстрее, чем с его дискретным аналогом. В результате ваша эффективность как дизайнера или техника по ремонту может значительно повыситься. Теперь вы можете сосредоточиться на системе, а не на характеристиках отдельного резистора смещения. Чтобы сделать многокаскадные усилители, просто соедините отдельные каскады вместе.
Пример \ (\ PageIndex {4} \)
Каков входной импеданс схемы на рисунке \ (\ PageIndex {5} \)? Что такое \ (V_ {out} \)? Как и в любом многокаскадном усилителе, входное сопротивление первого каскада равно системе \ (Z_ {in} \).{‘} = 8 дБВ \ notag \]
Поскольку 8 дБВ соответствует примерно 2,5 В, опасности ограничения также нет.
4.2.2: Инвертирующий усилитель напряжения
Инвертирующий усилитель основан на модели отрицательной обратной связи PP. Базовая форма показана на рисунке \ (\ PageIndex {6} \). Сама по себе эта форма измерения тока, а не напряжения. Для измерения напряжения добавлен входной резистор \ (R_i \). См. Рисунок \ (\ PageIndex {7} \). Вот как работает схема: \ (V_ {error} \) практически равен нулю, поэтому инвертирующий входной потенциал должен равняться неинвертирующему входному потенциалу.Это означает, что инвертирующий вход находится на виртуальной земле. Сигнал здесь настолько мал, что им можно пренебречь. Из-за этого мы также можем сказать, что импеданс, наблюдаемый при взгляде на эту точку, равен нулю. Последний пункт может вызвать некоторую путаницу. Вы можете спросить: «Как может быть нулевое сопротивление, если ток в операционном усилителе равен нулю?» Ответ заключается в том, что весь входящий ток будет проходить через \ (R_f \), минуя инвертирующий вход.
Рисунок \ (\ PageIndex {6} \): Базовый параллельно-параллельный усилитель.
Рисунок \ (\ PageIndex {7} \): Инвертирующий усилитель напряжения.
Подробное объяснение см. На Рисунке \ (\ PageIndex {8} \). Правый конец \ (R_i \) находится на виртуальной земле, поэтому все входное напряжение падает на нем, создавая \ (I_ {in} \) входной ток. Этот ток не может попасть в операционный усилитель, а вместо этого будет проходить через \ (R_f \). Поскольку на инвертирующий вход подается положительный сигнал, операционный усилитель потребляет выходной ток, таким образом протягивая \ (I_ {in} \) через \ (R_f \).Результирующее падение напряжения на \ (R_f \) имеет ту же величину, что и напряжение нагрузки. Это верно, потому что \ (R_f \) эффективно работает параллельно с нагрузкой. Обратите внимание, что оба элемента подключены к выходу операционного усилителя и (виртуальной) земле. Произошло изменение полярности, потому что мы связываем выходной сигнал с землей. Короче говоря, \ (V_ {out} \) — это инвертированное напряжение на \ (R_f \).
Рисунок \ (\ PageIndex {8} \): Анализ инвертирующего усилителя из рисунка \ (\ PageIndex {7} \).
\ [A_v = \ frac {V_ {out}} {V_ {in}} \ notag \]
\ [V_ {in} = I_ {in} R_i \ notag \]
\ [V_ {out} = −V_ {R_f} \ notag \]
\ [V_ {Rf} = I_ {in} R_f \ notag \]
Результат замещения
\ [A_v = — \ frac {I_ {in} R_f} {I_ {in} R_i} \ notag \]
\ [A_v = — \ frac {R_f} {R_i} \ label {4.2} \]
Опять же, мы видим, что коэффициент усиления по напряжению определяется соотношением резисторов. Опять же, есть допустимый диапазон значений.
Вышеупомянутое обсуждение указывает на вывод входного импеданса.Поскольку весь входной сигнал падает на \ (R_i \), отсюда следует, что весь источник возбуждения «видит» \ (R_i \). Проще говоря, \ (R_i \) устанавливает входное сопротивление. В отличие от неинвертирующего усилителя напряжения, существует определенная взаимосвязь между \ (Z_ {in} (R_i) \) и \ (A_v (-R_f / R_i) \). Это указывает на то, что с этой схемой очень сложно достичь высокого усиления и высокого \ (Z_ {in} \).
Пример \ (\ PageIndex {5} \)
Определите входное сопротивление и выходное напряжение для схемы, показанной на рисунке \ (\ PageIndex {9} \).
Рисунок \ (\ PageIndex {9} \): Инвертирующий усилитель для примера \ (\ PageIndex {9} \).
Входное сопротивление устанавливается как \ (R_i \). \ (R_i = 5 k \ Omega \), следовательно, \ (Z_ {in} = 5 k \ Omega \).
\ [V_ {out} = V_ {in} A_v \ notag \]
\ [A_v = — \ frac {R_f} {R_i} \ notag \]
\ [A_v = — \ frac {20 k} {5 k} \ notag \]
\ [A_v = −4 \ notag \]
\ [V_ {out} = 100 мВ \ раз (−4) \ notag \]
\ [V_ {out} = -400 мВ, \ text {(т. Е.э., перевернутый)} \ notag \]
Пример \ (\ PageIndex {6} \)
Разработайте инвертирующий усилитель с коэффициентом усиления 10 и входным сопротивлением 15 кОм (\ Omega \). Входное сопротивление говорит нам, что \ (R_i \) должно быть
.\ [Z_ {in} = R_i \ notag \]
\ [R_i = 15 k \ notag \]
Зная \ (R_i \), решите относительно \ (R_f \):
\ [A_v = — \ frac {R_f} {R_i} \ notag \]
\ [R_f = R_i (−A_v) \ notag \]
\ [R_f = 15k \ раз (- (- 10)) \ notag \]
\ [R_f = 150 к \ нотаг \]
Компьютерное моделирование
Моделирование Multisim результата примера \ (\ PageIndex {6} \) показано на рисунке \ (\ PageIndex {10} \) вместе со схемой.Это моделирование использует простую модель зависимого источника, представленную во второй главе. Для простоты вход установлен на 0,1 В постоянного тока. Обратите внимание, что выходной потенциал отрицательный, что указывает на инвертирующее действие усилителя. Также обратите внимание, что приближение виртуальной земли подтверждается довольно хорошо с инвертирующим входным потенциалом, измеряемым в области \ (\ mu \) V.
Рисунок \ (\ PageIndex {10a} \): Мультимедийное моделирование простой модели операционного усилителя для примера \ (\ PageIndex {6} \). а.Схема.
Рисунок \ (\ PageIndex {10b} \): Мультимедийное моделирование простой модели операционного усилителя для примера \ (\ PageIndex {6} \). б. Выходной листинг.
Пример \ (\ PageIndex {7} \)
Схема на рисунке \ (\ PageIndex {11} \) представляет собой каскад предварительного усилителя для электронной музыкальной клавиатуры. Как и у большинства музыкальных предусилителей, этот предлагает регулируемое усиление. Это достигается за счет следования за усилителем горшком. Каковы максимальные и минимальные значения усиления?
Рисунок \ (\ PageIndex {11} \): предусилитель музыкального инструмента для примера \ (\ PageIndex {7} \).
Обратите внимание, что коэффициент усиления для предусилителя является произведением коэффициента усиления операционного усилителя и коэффициента делителя напряжения, создаваемого потенциометром. Для максимального увеличения используйте горшок в самом верхнем положении. Поскольку потенциометр действует как делитель напряжения, самое верхнее положение не обеспечивает никакого действия делителя (т.е. его коэффициент усиления равен единице). Для средних частот 20 пФ можно игнорировать.
\ [A_ {v-max} = — \ frac {R_f} {R_i} \ notag \]
\ [A_ {v-max} = — \ frac {200 k} {15k} \ notag \]
\ [A_ {v-max} = — 13.{‘} = 22,5 дБ \ notag \]
Для минимального усиления горшок установлен на землю. В этот момент действие делителя бесконечно, и поэтому минимальное усиление равно 0 (что приводит к тишине).
\ (Z_ {in} \) для системы составляет около 15 к \ (\ Omega \). Что касается дополнительных компонентов, то конденсатор емкостью 20 пФ используется для уменьшения высокочастотного усиления. Два байпасных конденсатора 0,1 мкФ на линиях электропитания очень важны. Практически во всех схемах операционных усилителей используются байпасные конденсаторы.Из-за того, что операционные усилители обладают высоким коэффициентом усиления, важно иметь хорошее заземление переменного тока на выводах источника питания. На более высоких частотах индуктивность проводки источника питания может создавать значительное сопротивление. Это сопротивление может создать петлю положительной обратной связи, которой в противном случае не существовало бы. Без байпасных конденсаторов схема может генерировать колебания или генерировать ложные выходные сигналы. Точные значения конденсаторов обычно не критичны, обычно от 0,1 до 1 \ (\ mu \) F.
4.2.3: Преобразователь тока в напряжение
Как упоминалось ранее, инвертирующий усилитель напряжения основан на отрицательной обратной связи PP с дополнительным входным резистором, используемым для преобразования входного напряжения в ток.Что произойдет, если этот дополнительный резистор не использовать и использовать схему, подобную рис. \ (\ PageIndex {6} \)? Без дополнительного резистора вход находится на виртуальной земле, таким образом устанавливая \ (Z_ {in} \) на 0 \ (\ Omega \). Это идеально подходит для измерения тока. Этот входной ток проходит через \ (R_f \) и создает выходное напряжение, как указано выше. Характеристика преобразования тока в напряжение измеряется параметром transresistance. По определению, сопротивление этой цепи равно \ (R_f \).Чтобы найти \ (V_ {out} \), умножьте входной ток на сопротивление. Эта схема также меняет полярность.
\ [V_ {out} = −I_ {in} R_f \ label {4.3} \]
Пример \ (\ PageIndex {8} \)
Разработайте схему на основе рисунка \ (\ PageIndex {6} \), если входной ток -50 \ (\ mu \) A должен давать на выходе 4 В.
Трансмиссионное сопротивление цепи \ (R_f \)
\ [R_f = — \ frac {V_ {out}} {I_ {in}} \ notag \]
\ [R_f = — \ frac {4 V} {- 50 \ mu A} \ notag \]
\ [R_f = 80 k \ notag \]
Предполагается, что входной импеданс равен нулю.
На первый взгляд, схемы применения топологии, представленной в предыдущем примере, кажутся очень ограниченными. На самом деле существует ряд линейных интегральных схем, которые выдают свои выходные данные в виде тока 1 . Во многих случаях этот сигнал необходимо преобразовать в напряжение, чтобы должным образом взаимодействовать с другими элементами схемы. Для этой цели широко используется преобразователь тока в напряжение.
4.2.4: Неинвертирующий преобразователь напряжения в ток
В этой топологии схемы используется отрицательная обратная связь SS.Он определяет входное напряжение и вырабатывает ток. Можно провести концептуальное сравнение с полевым транзистором (источником тока, управляемым напряжением). Вместо усиления схемы нас интересует крутизна. Другими словами, сколько входного напряжения требуется для получения заданного выходного тока? Схема операционного усилителя, представленная здесь, управляет плавающей нагрузкой. То есть нагрузка не привязана к земле. В одних случаях это может быть удобно, а в других — неприятно. С некоторыми добавленными схемами можно создать версию с заземленной нагрузкой, хотя пространство не позволяет нам рассмотреть ее здесь.
Типичная схема «напряжение-ток» показана на рисунке \ (\ PageIndex {12} \). Поскольку здесь используется обратная связь типа последовательного ввода, мы можем сразу предположить, что \ (Z_ {in} \) бесконечно. Отношение напряжения к току устанавливается резистором обратной связи \ (R_i \). Поскольку \ (V_ {error} \) предполагается равным нулю, все \ (V_ {in} \) падает на \ (R_i \), создавая ток \ (I_ {Ri} \). Предполагается, что операционный усилитель имеет нулевой входной ток, поэтому весь \ (I_ {Ri} \) проходит через нагрузочный резистор \ (R_l \). Регулируя \ (R_i \), можно изменять ток нагрузки.
\ [I_ {load} = I_ {R_i} \ notag \]
\ [I_ {R_i} = \ frac {V_ {in}} {R_i} \ notag \]
\ [I_ {load} = \ frac {V_ {in}} {R_i} \ notag \]
Рисунок \ (\ PageIndex {12} \): Преобразователь напряжения в ток.
По определению
\ [g_m = \ frac {I_ {load}} {V_ {in}} \ notag \]
\ [g_m = \ frac {1} {R_i} \ label {4.4} \]
Итак, крутизна схемы задается резистором обратной связи. Как обычно, существуют практические ограничения на размер \ (R_i \).Если \ (R_i \) и \ (R_l \) слишком малы, существует вероятность, что операционный усилитель «исчерпает» выходной ток и перейдет в режим насыщения. С другой стороны, произведение двух резисторов и \ (I_ {load} \) не может превышать шины питания. Например, если \ (R_i \) плюс \ (R_l \) равно 10 к \ (\ Omega \), \ (I_ {load} \) не может превышать примерно 1,5 мА, если стандартное питание \ (\ pm \) 15 В используются.
Пример \ (\ PageIndex {9} \)
При входном напряжении 0,4 В в цепи, показанной на рисунке \ (\ PageIndex {13} \), каков ток нагрузки?
\ [g_m = \ frac {1} {R_i} \ notag \]
\ [g_m = \ frac {1} {20 тыс.} \ Notag \]
\ [g_m = 50 \ mu S \ notag \]
\ [I_ {load} = g_m V_ {in} \ notag \]
\ [I_ {load} = 50 \ mu S \ times 0.4 В \ notag \]
\ [I_ {load} = 20 \ mu A \ notag \]
Рисунок \ (\ PageIndex {13} \): преобразователь напряжения в ток для примера \ (\ PageIndex {9} \).
Здесь нет опасности перегрузки по току, так как средний операционный усилитель может выдавать максимум около 20 мА. Выходной ток будет 20 \ (\ mu \) A независимо от значения \ (R_l \), вплоть до ограничения. Опасности отсечения в этой ситуации тоже нет. Напряжение на выходе операционного усилителя на землю равно
.\ [V_ {max} = (R_i + R_l) I_ {load} \ notag \]
\ [V_ {max} = (20 k + 1k) \ times 20 \ mu A \ notag \]
\ [V_ {max} = 420 мВ \ notag \]
Это намного ниже уровня отсечения.
Компьютерное моделирование
Моделирование схемы из примера \ (\ PageIndex {9} \) показано на рисунке \ (\ PageIndex {14} \). Для упрощения компоновки была выбрана идеальная модель операционного усилителя Multisim. Ток нагрузки точно такой, как рассчитанный, при 20 мкА. Здесь используется интересный трюк для построения графика тока нагрузки, поскольку многие симуляторы предлагают только график узловых напряжений. Используя постпроцессор Multisim, ток нагрузки вычисляется путем взятия разницы между напряжениями узлов по обе стороны от нагрузочного резистора и последующего деления результата на сопротивление нагрузки.
Рисунок \ (\ PageIndex {14a} \): Схема моделирования преобразователя напряжения в ток.
Рисунок \ (\ PageIndex {14b} \): Результаты моделирования.
Пример \ (\ PageIndex {10} \)
Схема на рисунке \ (\ PageIndex {15} \) может использоваться для изготовления вольтметра постоянного тока с высоким входным сопротивлением. Нагрузка в этом случае представляет собой простое движение счетчика. Этот конкретный измеритель требует 100 \ (\ mu \) A для полного отклонения. Если мы хотим измерить напряжения до 10 В, что должно быть \ (R_i \)?
Во-первых, мы должны найти крутизну.
\ [g_m = \ frac {I_ {load}} {V_ {in}} \ notag \]
\ [g_m = \ frac {100 \ mu A} {10 V} \ notag \]
\ [g_m = 10 \ mu S \ notag \]
\ [R_i = \ frac {1} {g_m} \ notag \]
\ [R_i = \ frac {1} {10 \ mu S} \ notag \]
\ [R_i = 100 к \ нотаг \]
Рисунок \ (\ PageIndex {15} \): вольтметр постоянного тока для примера \ (\ PageIndex {10} \).
Отклонение счетчика предполагается линейным. Например, если входной сигнал составляет всего 5 В, производимый ток уменьшается вдвое до 50 \ (\ mu \) A.50 \ (\ mu \) A должны давать отклонение в половину шкалы. Точность этого электронного вольтметра зависит от точности \ (R_i \) и линейности движения измерителя. Обратите внимание, что эта маленькая схема может быть очень удобна в лаборатории, питаясь от батарей. Для изменения шкалы новые значения \ (R_i \) могут быть заменены поворотным переключателем. Для шкалы 1 В \ (R_i \) равно 10 к \ (\ Omega \). Обратите внимание, что для более высоких входных диапазонов требуется какой-либо входной аттенюатор. Это связано с тем, что большинство операционных усилителей могут быть повреждены, если используются входные сигналы, превышающие длину шин питания.
4.2.5: Инвертирующий усилитель тока
Инвертирующий усилитель тока использует отрицательную обратную связь PS. Как и в преобразователе напряжения в ток, нагрузка плавающая. Базовая схема показана на рисунке \ (\ PageIndex {16} \). Из-за параллельного подключения отрицательной обратной связи на входе предполагается, что входной импеданс схемы равен нулю. Это означает, что точка входа находится на виртуальной земле. Ток в операционном усилителе незначителен, поэтому весь входной ток течет через \ (R_i \) к узлу A.Фактически, \ (R_i \) и \ (R_f \) параллельны (они оба имеют общий узел A и землю; фактически виртуальная земля для \ (R_i \)). Следовательно, \ (V_ {Ri} \) и \ (V_ {Rf} \) — одно и то же значение. Это означает, что ток течет через \ (R_f \) от земли к узлу A. Эти два тока соединяются, образуя ток нагрузки. Таким образом достигается текущий коэффициент усиления. Чем больше \ (I_ {Rf} \) относительно \ (I_ {in} \), тем больше текущий коэффициент усиления. Поскольку в операционном усилителе падает ток, это инвертирующий усилитель.
Рисунок \ (\ PageIndex {16} \): Инвертирующий усилитель тока
\ [A_i = — \ frac {I_ {out}} {I_ {in}} \ notag \]
\ [I_ {out} = I_ {Rf} + I_ {Ri} \ label {4.5} \]
\ [I_ {Ri} = I_ {in} \ notag \]
\ [I_ {Rf} = \ frac {V_ {Rf}} {R_f} \ notag \]
Поскольку \ (V_ {Rf} \) — это то же значение, что и \ (V_ {Ri} \),
\ [I_ {Rf} = \ frac {V_ {Ri}} {R_f} \ label {4.6} \]
\ [V_ {Ri} = I_ {дюйм} R_i \ label {4.7} \]
Замена \ ref {4.7} на \ ref {4.6} дает
\ [I_ {Rf} = \ frac {I_ {in} R_i} {R_f} \ notag \]
Подстановка в \ ref {4.5} дает
\ [I_ {out} = I_ {in} + \ frac {I_ {in} R_i} {R_f} \ notag \]
\ [I_ {out} = I_ {in} \ left (1+ \ frac {R_i} {R_f} \ right) \ notag \]
\ [A_i = — \ left (1+ \ frac {R_i} {R_f} \ right) \ label {4.8} \]
Как и следовало ожидать, коэффициент усиления зависит от двух резисторов обратной связи. Обратите внимание на сходство этого результата с неинвертирующим усилителем напряжения.
Пример \ (\ PageIndex {11} \)
Каков ток нагрузки на рисунке \ (\ PageIndex {17} \)?
Рисунок \ (\ PageIndex {17} \): усилитель тока для примера \ (\ PageIndex {11} \).
\ [I_ {out} = −A_i I_ {in} \ notag \]
\ [A_i = — (1+ \ frac {R_i} {R_f}) \ notag \]
\ [A_i = — (1+ \ frac {33 k} {1 k}) \ notag \]
\ [A_i = −34 \ notag \]
\ [I_ {out} = −34 \ times 5 \ mu A \ notag \]
\ [I_ {out} = −170 \ mu A \ text {(тонущий)} \ notag \]
Нам нужно убедиться, что этот ток не вызывает ограничения на выходе.Все, что вам нужно — это простая проверка по закону Ома.
\ [V_ {max} = I_ {out} R_ {load} + I_ {in} R_i \ notag \]
\ [V_ {max} = 170 \ mu A \ times 10 k + 5 \ mu A \ times 33k \ notag \]
\ [V_ {max} = 1,7 В + 0,165 В \ notag \]
\ [V_ {max} = 1,865 В \ text {(без проблем)} \ notag \]
Пример \ (\ PageIndex {12} \)
Разработайте усилитель с коэффициентом усиления по току -50. Нагрузка примерно 200 к \ (\ Омега \). Предполагая типичный операционный усилитель (\ (I_ {out-max} \) = 20 мА с \ (\ pm \) источниками питания 15 В), каков максимально достижимый ток нагрузки?
\ [A_i = — \ left (1+ \ frac {R_i} {R_f} \ right) \ notag \]
\ [\ frac {R_i} {R_f} = −Ai −1 \ notag \]
\ [\ frac {R_i} {R_f} = 50-1 \ notag \]
\ [\ frac {R_i} {R_f} = 49 \ notag \]
Следовательно, \ (R_i \) должен быть в 49 раз больше, чем \ (R_f \).Возможные решения включают:
\ [R_i = 49k \ Omega, R_f = 1 k \ Omega \ notag \]
\ [R_i = 98 k \ Omega, R_f = 2 k \ Omega \ notag \]
\ [R_i = 24,5 k \ Omega, R_f = 500 \ Omega \ notag \]
Что касается максимального тока нагрузки, он не может быть больше, чем максимальный выход операционного усилителя в 20 мА, но может быть меньше. Нам нужно определить ток при отсечении. Из-за большого сопротивления нагрузки практически весь выходной потенциал будет падать на него.Игнорирование дополнительного падения на резисторах обратной связи приведет к ошибке не более 1% (это наихудший случай, если предположить, что набор резисторов номер два).
Рисунок \ (\ PageIndex {18} \): Конструкция усилителя тока для примера \ (\ PageIndex {12} \).
С шинами 15 В обычный операционный усилитель будет ограничивать напряжение 13,5 В. Результирующий ток находится по закону Ома:
\ [I_ {max} = \ frac {13,5 V} {200 k} \ notag \]
\ [I_ {max} = 67,5 \ mu A \ notag \]
Другой способ взглянуть на это — сказать, что максимально допустимый входной ток равен 67.5 \ (\ mu \) A / 50 или 1,35 \ (\ mu \) A. Одно из возможных решений показано на рисунке \ (\ PageIndex {18} \).
4.2.6: Суммирующие усилители
В схемотехнике очень распространено объединение нескольких сигналов в один общий сигнал. Хорошим примером этого является индустрия вещания и звукозаписи. Типичная современная запись музыки потребует использования, возможно, десятков микрофонов, но конечный продукт обычно состоит из двух выходных сигналов (стерео левого и правого). Если сигналы объединяются бессистемно, это может привести к чрезмерным помехам, шумам и искажениям.Идеальный суммирующий усилитель будет представлять каждый входной сигнал с изолированной нагрузкой, на которую не влияют другие каналы.
Самая распространенная форма суммирующего усилителя на самом деле представляет собой не что иное, как расширение инвертирующего усилителя напряжения. Поскольку вход операционного усилителя находится на виртуальной земле, он представляет собой идеальный узел суммирования тока. Вместо размещения одного входного резистора в этой точке можно использовать несколько входных резисторов. Каждый входной источник управляет своим собственным резистором, и соседние входы практически не влияют на него.Виртуальная земля — это ключ. Общий суммирующий усилитель показан на рисунке \ (\ PageIndex {19} \).
Рисунок \ (\ PageIndex {19} \): Суммирующий усилитель.
Входное сопротивление для первого канала равно \ (R_ {i1} \), а коэффициент усиления по напряжению равен \ (- R_f / R_ {i1} \). Для канала 2 входной импеданс равен \ (R_ {i2} \) с усилением \ (- R_f / R_ {i2} \). В общем то для канала N имеем
\ [Z_ {in N} = R_ {i N} \ notag \]
\ [A_ {v N} = — \ frac {R_f} {R_ {i N}} \ notag \]
Выходной сигнал — это сумма всех входов, умноженная на их соответствующие коэффициенты усиления.{n} {V_ {in_i} A_ {v_i}} \ label {4.9} \]
Суммирующий усилитель может иметь одинаковое усиление для каждого входного канала. Это называется равновзвешенной конфигурацией.
Пример \ (\ PageIndex {13} \)
Каков выходной сигнал суммирующего усилителя на рисунке \ (\ PageIndex {20} \) при заданных входных напряжениях постоянного тока?
Рисунок \ (\ PageIndex {20} \): Суммирующий усилитель для примера \ (\ PageIndex {13} \).
Самый простой способ приблизиться к этому — просто рассматривать схему как три инвертирующих усилителя напряжения, а затем складывать результаты, чтобы получить окончательный выходной сигнал.
Канал 1:
\ [A_v = — \ frac {R_f} {R_i} \ notag \]
\ [A_v = — \ frac {10 k} {4 k} \ notag \]
\ [A_v = −2,5 \ notag \]
\ [V_ {out} = −2,5 \ умножить на 1V \ notag \]
\ [V_ {out} = −2,5 В \ notag \]
Канал 2:
\ [A_v = — \ frac {R_f} {R_i} \ notag \]
\ [A_v = — \ frac {10 k} {2 k} \ notag \]
\ [A_v = −5 \ notag \]
\ [V_ {out} = −5 \ times −2 V \ notag \]
\ [V_ {out} = 10 В \ notag \]
Канал 3:
\ [A_v = — \ frac {R_f} {R_i} \ notag \]
\ [A_v = — \ frac {10 k} {1 k} \ notag \]
\ [A_v = −10 \ notag \]
\ [V_ {out} = −10 \ раз.5 В \ notag \]
\ [V_ {out} = −5 В \ notag \]
Окончательный результат находится путем суммирования:
\ [V_ {out} = −2,5 В + 10 В + (- 5 В) \ notag \]
\ [V_ {out} = 2,5 В \ notag \]
Если бы входы были сигналами переменного тока, суммирование не было бы таким простым. Помните, что сигналы переменного тока разной частоты и фазы не складываются когерентно. Вы можете выполнить расчет, аналогичный предыдущему, чтобы найти пиковое значение, однако для эффективного значения требуется расчет RMS (т.е., квадратный корень из суммы квадратов).
Для использования в вещательной и звукозаписывающей индустрии суммирующие усилители также потребуют некоторой формы регулировки громкости для каждого входного канала, а также основного регулятора громкости. Это позволяет правильно сбалансировать уровни различных микрофонов или инструментов. Теоретически регулировку усиления для отдельного канала можно произвести, заменив каждый входной резистор потенциометром. Регулируя \ (R_i \), можно напрямую изменять усиление. На практике с такой компоновкой возникает несколько проблем.Во-первых, невозможно полностью выключить канал. Требуемое значение для \ (R_i \) будет бесконечным. Во-вторых, поскольку \ (R_i \) устанавливает входное сопротивление, изменение усиления приведет к изменению \ (Z_ {in} \). Это изменение может привести к перегрузке или изменению характеристик источника возбуждения. Одно из возможных решений — сохранить фиксированное значение \ (R_i \) и поместить перед ним потенциометр, как показано на рисунке \ (\ PageIndex {21} \). Банк производит усиление от 1 до 0. Комбинация \ (R_f / R_i \) затем устанавливается на максимальное усиление.Пока \ (R_i \) в несколько раз больше, чем значение потенциометра, входное сопротивление канала будет оставаться относительно постоянным. Эффективный \ (Z_ {in} \) для канала равен \ (R_ {pot} \) параллельно с \ (R_i \), как минимум, до \ (R_ {pot} \).
Рисунок \ (\ PageIndex {21} \): Аудиомикшер.
Что касается общего регулятора громкости, можно использовать потенциометр для \ (R_f \). Однако без ограничивающего резистора очень низкое задающее усиление может привести к перегрузке операционного усилителя из-за небольшого эффективного значения \ (R_f \).Этот метод также вызывает изменения в потенциалах смещения и полосе пропускания цепи. Техника, которая обеспечивает более высокую производительность, включает использование этапа с фиксированным значением \ (R_f \), за которым следует горшок, как на рисунке \ (\ PageIndex {21} \).
Еще одним применением суммирующего усилителя является устройство сдвига уровня. Сдвигатель уровня представляет собой суммирующий усилитель с двумя входами. Один вход — это желаемый сигнал переменного тока, а второй вход — значение постоянного тока. Правильный выбор значения постоянного тока позволяет разместить сигнал переменного тока с желаемым смещением постоянного тока.У такой схемы есть много применений. Одним из возможных приложений является управление смещением постоянного тока, доступное на многих генераторах сигналов.
4.2.7: Неинвертирующий суммирующий усилитель
Помимо инвертирующей формы, суммирующие усилители могут быть изготовлены и в неинвертирующей форме. Неинвертирующее лето обычно демонстрирует лучшие высокочастотные характеристики по сравнению с инвертирующим типом. Одна из возможных схем показана на рисунке \ (\ PageIndex {22} \). В этом примере показаны три входа, хотя можно добавить и другие.С каждым входом связан входной резистор. Обратите внимание, что невозможно просто соединить несколько источников вместе в надежде суммировать их соответствующие сигналы. Это связано с тем, что каждый источник будет пытаться привести свой вывод к желаемому значению, которое будет отличаться от значений, созданных другими источниками. Возникающий дисбаланс может вызвать чрезмерные (и, возможно, повреждающие) токи источника. Следовательно, каждый источник должен быть изолирован от других через резистор.
Рисунок \ (\ PageIndex {22} \): Неинвертирующий суммирующий усилитель.
Чтобы понять работу этой схемы, лучше всего разбить ее на две части: часть входного источника / резистора и часть неинвертирующего усилителя. Входные сигналы объединяются для создания общего входного напряжения \ (V_t \). При осмотре вы должны увидеть, что выходное напряжение схемы будет в \ (V_t \) раз больше неинвертирующего усиления, или
.\ [V_ {out} = V_t \ left (1+ \ frac {R_f} {R_i} \ right) \ notag \]
Осталось только определить \ (V_t \).Каждый из входных каналов вносит вклад в \ (V_t \) аналогичным образом, поэтому достаточно получить вклад от одного канала.
Рисунок \ (\ PageIndex {23} \): Эквивалентная схема входа канала 1.
В отличие от инвертирующего лета, неинвертирующее лето не использует преимущества узла суммирования виртуальной земли. В результате отдельные каналы будут влиять друг на друга. Эквивалентная схема для канала 1 перерисована на рисунке \ (\ PageIndex {23} \).Используя суперпозицию, мы сначала заменим входные генераторы каналов 2 и 3 на короткие замыкания. В результате получается простой делитель напряжения между \ (V_1 \) и \ (V_ {t1} \).
\ [V_ {t 1} = V_1 \ frac {R_2 || R_3} {R_1 + R_2 || R_3} \ notag \]
Аналогичным образом мы можем получить части \ (V_t \) из-за канала 2
\ [V_ {t 2} = V_2 \ frac {R_1 || R_3} {R_2 + R_1 || R_3} \ notag \]
и по 3 каналу
\ [V_ {t 3} = V_3 \ frac {R_1 || R_2} {R_3 + R_1 || R_2} \ notag \]
\ (V_t \) — это сумма этих трех частей.
\ [V_t = V_ {t 1} + V_ {t 2} + V_ {t 3} \ notag \]
Таким образом, объединив эти элементы, находим, что выходное напряжение равно
\ [V_ {out} = \ left (1+ \ frac {R_f} {R_i} \ right) \ left (V_1 \ frac {R_2 || R_3} {R_1 + R_2 || R_3} + V_2 \ frac {R_1 ») || R_3} {R_2 + R_1 || R_3} + V_3 \ frac {R_1 || R_2} {R_3 + R_1 || R_2} \ right) \ notag \]
Для удобства и равного взвешивания входные резисторы часто устанавливаются на одно и то же значение. В результате получается схема, которая усредняет вместе все входы.{n} {V_n}} {n} \ label {4.10} \]
, где \ (n \) — количество каналов.
Одна проблема все еще остается с этой схемой, и это межканальная изоляция или перекрестные помехи. Этого можно избежать путем индивидуальной буферизации каждого ввода, как показано на рисунке \ (\ PageIndex {24} \).
Рисунок \ (\ PageIndex {24} \): Буферизованный и изолированный неинвертирующий суммирующий усилитель.
Пример \ (\ PageIndex {14} \)
Неинвертирующее лето, такое как показанное на рисунке \ (\ PageIndex {22} \), используется для объединения трех сигналов.\ (V_1 \) = 1 В постоянного тока, \ (V_2 \) = -0,2 В постоянного тока и \ (V_3 \) представляет собой синусоидальную волну с пиковым напряжением 2 В и частотой 100 Гц. Определите выходное напряжение, если \ (R_1 = R_2 = R_3 = R_f \) = 20 к \ (\ Omega \) и \ (R_i \) = 5 к \ (\ Omega \).
Поскольку все входные резисторы равны, мы можем использовать общую форму уравнения суммирования.
\ [V_ {out} = \ left (1+ \ frac {R_f} {R_i} \ right) \ frac {V_1 + V_2 + \ dpts + V_n} {\ text {Количество каналов}} \ notag \]
\ [V_ {out} = \ left (1+ \ frac {20 k} {5 k} \ right) \ frac {1 VDC + (- 0.2 В постоянного тока) +2 \ sin2 \ pi 100 t} {3} \ notag \]
\ [V_ {out} = 5 \ frac {0,8 В постоянного тока + 2 \ sin2 \ pi 100 t} {3} \ notag \]
\ [V_ {out} = 1,33 В постоянного тока + 3,33 \ sin2 \ pi 100 t \ notag \]
Итак, мы видим, что на выходе получается пиковая синусоидальная волна 3,33 В при смещении 1,33 В постоянного тока.
4.2.8: Дифференциальный усилитель
Пока операционный усилитель основан на дифференциальном входном каскаде, ничто не мешает вам сделать с ним дифференциальный усилитель. Применение блока на базе операционного усилителя такое же, как и у дискретной версии, рассмотренной в первой главе.По сути, конфигурация дифференциального усилителя представляет собой комбинацию инвертирующего и неинвертирующего усилителей напряжения. Кандидат показан на рисунке \ (\ PageIndex {25} \). Анализ идентичен анализу двух базовых типов, и для объединения результатов используется суперпозиция. Очевидная проблема для этой схемы состоит в том, что при использовании более низких значений возникает большое несоответствие между коэффициентами усиления. Помните, что для инвертирующего входа величина усиления равна \ (R_f / R_i \), тогда как неинвертирующий вход видит \ (R_f / R_i \) + 1.Для правильной работы коэффициенты усиления двух половинок должны быть одинаковыми. Неинвертирующий вход имеет немного большее усиление, поэтому для компенсации можно использовать простой делитель напряжения. Это показано на рисунке \ (\ PageIndex {26} \). Соотношение должно быть таким же, как соотношение \ (R_f / R_i \). Целевое усиление равно \ (R_f / R_i \), текущее усиление равно 1 + \ (R_f / R_i \), которое может быть записано как \ ((R_f + R_i) / R_i \). Для компенсации используется коэффициент усиления \ (R_f / (R_f + R_i) \).
Рисунок \ (\ PageIndex {25} \): кандидат в дифференциальный усилитель.{‘} \) равный \ (R_i \). Это позволит поддерживать примерно равное входное сопротивление между двумя половинами, если используются два разных источника входного сигнала.
После добавления делителя выходное напряжение определяется умножением дифференциального входного сигнала на \ (R_f / R_i \).
Пример \ (\ PageIndex {15} \)
Разработайте простой дифференциальный усилитель с входным сопротивлением 10 кОм на ножку и коэффициентом усиления по напряжению 26 дБ.
Прежде всего, преобразование 26 дБ в обычную форму дает 20.{‘} = 9,52 тыс. \ Notag \]
Окончательный результат показан на рисунке \ (\ PageIndex {27} \). Как вы увидите позже в шестой главе, дифференциальный усилитель занимает видное место в другой полезной схеме — инструментальном усилителе.
Рисунок \ (\ PageIndex {27} \): Разностный усилитель для примера \ (\ PageIndex {15} \).
4.2.9: Сумматор / вычитатель
Если инвертирующий и неинвертирующий суммирующие усилители комбинируются с использованием топологии дифференциального усилителя, получается сумматор / вычитатель.Обычно все резисторы в сумматоре / вычитателе имеют одинаковое значение. Типичный сумматор / вычитатель показан на рисунке \ (\ PageIndex {28} \).
Рисунок \ (\ PageIndex {28} \): Сумматор-вычитатель.
Число инвертирующих входов от 1 до \ (m \) и количество неинвертирующих входов от \ (m + 1 \) до \ (n \). Схема может быть проанализирована путем объединения предыдущих доказательств уравнений от \ ref {4.9} до \ ref {4.11} с помощью теоремы суперпозиции. Детали оставлены в качестве упражнения ( Задача 4.{m} {V_ {i n_j}} \ label {4.12} \]
По сути, вы можете думать о выходном напряжении в терминах вычитания инвертирующего входного суммирования из неинвертирующего входного суммирования.
4.2.10: Регулируемый инвертор / неинвертор
Уникальный усилитель с регулируемым коэффициентом усиления показан на рисунке \ (\ PageIndex {29} \). Что делает эту схему интересной, так это то, что коэффициент усиления непрерывно изменяется от инвертирующего до неинвертирующего максимума. Например, усиление может быть установлено максимум на 10.Полный оборот потенциометра изменит коэффициент усиления от +10 до -10. Точная средняя установка даст усиление 0. Таким образом, одна ручка управляет как фазой, так и величиной усиления.
Рисунок \ (\ PageIndex {29} \): Регулируемый инвертор / неинвертор.
Для анализа схемы см. Рисунок \ (\ PageIndex {30} \).
Рисунок \ (\ PageIndex {30} \): инверторный / неинверторный анализ.
Как и следовало ожидать, коэффициент усиления схемы определяется как отношение выходного напряжения к входному.Важно отметить, что в отличие от обычного инвертирующего усилителя величина выходного напряжения не обязательно равна напряжению на \ (R_2 \). Это связано с тем, что инвертирующий вывод операционного усилителя обычно не является виртуальной землей. Вместо этого также необходимо учитывать напряжение на \ (R_3 \). Поскольку два входа операционного усилителя должны иметь примерно одинаковый потенциал (т.е. \ (V_ {error} \) должен быть 0), напряжение на инвертирующей клемме должно быть таким же, как напряжение, снимаемое с потенциометра.Представляя коэффициент делителя напряжения потенциометра как \ (k \), находим:
\ [V_ {out} = k V_ {i n} -V_ {R2} \ label {4.13} \]
Падение на \ (R_2 \) просто \ (I_2 R_2 \). \ (I_2 \) находится по закону тока Кирхгофа и соответствующей замене резистора напряжения:
\ [I_2 = I_1 — I_3 \ notag \]
\ [I_2 = \ frac {V_ {i n} −k V_ {i n}} {R_1} — \ frac {k V_ {i n}} {R_3} \ notag \]
\ [I_2 = V_ {i n} \ left (\ frac {1 − k} {R_1} — \ frac {k} {R_3} \ right) \ notag \]
Таким образом, V_ {R2} оказывается равным
.\ [V_ {R2} = V_ {i n} \ left ((1 − k) \ frac {R_2} {R_1} — k \ frac {R_2} {R_3} \ right) \ label (4.14) \]
Комбинируя уравнения \ ref {4.13} и \ ref {4.14} и затем решая для усиления, находим
\ [A_v = k− \ left ((1 − k) \ frac {R_2} {R_1} −k \ frac {R_2} {R_3} \ right) \ notag \]
\ [A_v = k− \ left (\ frac {R_2} {R_1} −k \ frac {R_2} {R_1} −k \ frac {R_2} {R_3} \ right) \ notag \]
\ [A_v = — \ frac {R_2} {R_1} + k \ left (1+ \ frac {R_2} {R_1} + k \ frac {R_2} {R_3} \ right) \ notag \]
Значение \ (R_3 \) выбрано так, чтобы \ (R_1 = R_2 || R_3 \). Это означает, что
\ [R_3 = \ frac {1} {\ frac {1} {R_1} — \ frac {1} {R_2}} \ notag \]
Подставляя это в наше уравнение усиления и упрощая, дает
\ [A_v = \ frac {R_2} {R_1} (2k − 1) \ notag \]
По сути, резисторы \ (R_1 \) и \ (R_2 \) устанавливают максимальное усиление.Потенциометр устанавливает \ (k \) от 0 до 1. Если \ (k = 1 \), то \ (A_v = R_2 / R_1 \) или максимальное неинвертирующее усиление. Когда \ (k = 0 \), то \ (A_v = — R_2 / R_1 \) или максимальное усиление инвертирования. Наконец, когда потенциометр установлен в среднюю точку, \ (k = 0,5 \) и \ (A_v = 0 \).
Список литературы
1 В первую очередь, операционные усилители крутизны и цифро-аналоговые преобразователи, которые мы рассмотрим в главах шестой и двенадцатой соответственно.
Усилитель, аттенюатор или оба? | Analog Devices
ВОПРОС:
Могу ли я использовать усилитель в качестве аттенюатора?
Ответ:
Интересный вопрос.На первый взгляд это кажется нелогичным, но на самом деле есть несколько очень веских причин, по которым кто-то может захотеть это сделать. Одна очень полезная функция операционного усилителя — это преобразование импеданса. Использование пассивного аттенюатора перед операционным усилителем или использование самого усилителя в качестве аттенюатора позволяет в полной мере использовать эту функцию. Однако следует принять некоторые меры предосторожности.
При использовании усилителя в качестве аттенюатора коэффициент усиления усилителя меньше единицы (G <1). Поэтому предполагается, что усилитель должен быть сконфигурирован как инвертор.Это связано с тем, что уравнение инвертирующего усиления имеет вид G = –RF / RG, а уравнение неинвертирующего усиления - G = (RF / RG) +1. Быстрый осмотр показывает, что единственной жизнеспособной конфигурацией усилителя / аттенюатора должна быть инвертирующая. Ну не обязательно; как упоминалось ранее, пассивный аттенюатор перед неинвертирующим усилителем будет работать и обеспечивать неинвертированный выходной сигнал. Вы также можете использовать дифференциальный усилитель или дифференциальный усилитель; оба используют уравнение усиления G = RF / RG. Таким образом, в качестве аттенюаторов можно использовать как инвертирующие, так и неинвертирующие конфигурации операционных усилителей... или как усилители.
Я упомянул, что необходимо соблюдать некоторые меры предосторожности при использовании усилителей в качестве аттенюаторов. Первый — когда используются очень большие значения сопротивления обратной связи. Это имеет несколько последствий: больший системный шум, большие напряжения смещения и стабильность. Большие резисторы обратной связи, наряду с входом усилителя и паразитной емкостью, могут вносить полюс в отклик обратной связи усилителя, что вызывает дополнительный фазовый сдвиг, который снижает запас по фазе усилителя и может привести к нестабильности.
Более важным фактором является усиление шума и его отношение к стабильности усилителя. Помните, что именно усиление шума, а не усиление сигнала определяет стабильность усилителя. Коэффициент усиления шума, который одинаков как для инвертирующей, так и для неинвертирующей конфигураций усилителя, равен уравнению для неинвертирующего усиления. Например, если инвертирующий усилитель имеет коэффициент усиления сигнала -0,5, он все равно имеет коэффициент усиления шума 1,5. После определения коэффициента усиления шума его можно перенести на график усиления и фазы без обратной связи для проверки запаса по фазе и стабильности.Если при выбранном коэффициенте усиления шума имеется запас по фазе не менее 45 °, усилитель будет работать нормально, если менее 45 °, могут возникнуть проблемы. Существуют и другие способы увеличения усиления шума при сохранении низкого усиления сигнала, но для этого придется подождать до следующего RAQ.
Неинвертирующий усилитель — обзор
Разработайте схему неинвертирующего усилителя с коэффициентом усиления 500.
Разработайте инвертирующий усилитель с регулируемым коэффициентом усиления от 50 до 250.
Какова ширина полосы у следующего неинвертирующего усилителя? Если бы та же самая сеть обратной связи использовалась для разработки инвертирующего усилителя, какой была бы полоса пропускания этой схемы?
Усилитель имеет коэффициент усиления 10 МГц. Он используется в неинвертирующем усилителе, где β = 0,01. Какой коэффициент усиления у усилителя? Какая пропускная способность?
LF 356 используется для реализации усилителя с регулируемым усилением в Примере 15.3. Каковы полосы пропускания этой схемы при двух крайних значениях усиления?
Конденсатор емкостью 0,001 мкФ добавлен в цепь обратной связи следующей схемы инвертирующего операционного усилителя. Можно предположить, что до добавления конденсатора сдвиг фазы из-за усилителя при Avβ = 1 составлял 120 градусов. (Напомним, критерий стабильности заключается в том, что фазовый сдвиг, вызванный операционным усилителем и цепью обратной связи, должен быть меньше 180 градусов, когда Avβ = 1.) Каков фазовый сдвиг ОУ плюс цепь обратной связи после добавления конденсатора на частоте, где Avβ = 1? Следуйте примеру, приведенному в разделе о стабильности.
Для следующей схемы предположим, что R 1 = 500 кОм, R f = 1,0 МОм и R eq = параллельная комбинация R 1 и R f .Какое полное напряжение смещения на выходе? Насколько увеличивается это напряжение смещения, если R eq заменяется коротким замыканием?
Выведите передаточную функцию следующей схемы сумматора. Используйте KVL, примененный к узлу A.
Найдите общий шум на выходе следующей схемы. Определите основной источник (и) шума. Каким будет выходной шум, если резистор заземления 50 кОм на положительной клемме заменить коротким замыканием? (Обратите внимание, что этот резистор увеличивает как шум Джонсона от резисторов, так и шум напряжения, создаваемый шумовым током операционного усилителя.)
Какой минимальный сигнал для схемы из Задачи 9 может быть обнаружен при ОСШ 10 дБ? Какое будет напряжение такого сигнала при В на выходе ?
Шумовой ток операционного усилителя составляет 0,1 пА√Гц. Этот операционный усилитель используется как усилитель крутизны (рисунок 15.31). Каким должно быть минимальное значение сопротивления обратной связи, чтобы вклад шума резистора был меньше, чем вклад шума операционного усилителя?
Разработайте однополюсный фильтр нижних частот с полосой пропускания 1 кГц. Предположим, у вас есть конденсаторы емкостью 0,001, 0,01, 0,05 и 0,1 мкФ и широкий диапазон резисторов.
Разработайте двухполюсный фильтр нижних частот с частотой среза 500 Гц и коэффициентом демпфирования 0,8. Предположим, что тот же компонент доступен, что и в Задаче 15.
Разработайте двухполюсный фильтр верхних частот с частотой среза 10 кГц и коэффициентом демпфирования 0.707. (Схема для фильтра верхних частот такая же, как и для фильтра нижних частот, за исключением того, что конденсаторы и резисторы поменяны местами, как показано на следующем рисунке.)
Разработка инструментального усилителя с переключаемым усилением 10, 100 и 1000. (Подсказка: включите или отключите необходимые резисторы в цепи по мере необходимости.)
Как получить передаточную функцию неинвертирующего усилителя — Освоение конструкции электроники
Один из наиболее распространенных усилителей в аналоговой конструкции — это неинвертирующий усилитель.
Рисунок 1
Его передаточная функция
| (1) |
Как получить эту функцию?
Прежде всего отметим, что этот операционный усилитель можно считать идеальным. Таким образом, ток на инвертирующем входе равен нулю (I = 0A, см. Рисунок 2), а токи через R1 и R2 равны.
| (2) |
Рисунок 2
Затем мы можем написать уравнение для цикла, созданного Vout, R2, V и Vin.
| (3) |
Из уравнения (3) выражение I2 равно
| (4) |
Аналогичным образом мы можем определить выражение для I1. Уравнение (5) является уравнением петли для R1, V1 и Vin.
| (5) |
и
| (6) |
Будучи идеальным операционным усилителем, мы можем считать, что неинвертирующий вход имеет тот же потенциал, что и инвертирующий вход, поэтому V = 0 В.Это связано с высоким коэффициентом усиления идеального операционного усилителя. Когда выход находится на уровне нескольких вольт, дифференциальный вход может быть на уровне нескольких десятков микровольт. Следовательно, V очень близко к нулю.
Заменив I1 и I2 в уравнении (2) и исключив V, мы можем записать это уравнение:
| (7) |
Следовательно, передаточная функция неинвертирующего усилителя равна
| (8) |
Q.E. D.
Инвертирующий и неинвертирующий усилители и их различия
Термин «операционный усилитель» или операционный усилитель в основном означает устройство усиления напряжения. Он использует внешние компоненты обратной связи между своими входами, а также выходные клеммы, такие как резисторы и конденсаторы. Идеальный операционный усилитель имеет разные характеристики, включая бесконечное усиление разомкнутого контура, бесконечное входное сопротивление, нулевое сопротивление o / p, нулевое смещение и высокую полосу пропускания. Операционный усилитель включает в себя три терминала, а именно два входа и один выход.Две входные клеммы инвертируют и не инвертируют, а третья клемма — выход. Эти усилители широко используются для выполнения математических операций и преобразования сигналов, поскольку они почти идеальны для усиления постоянного тока. В этой статье обсуждается основное различие между инвертирующим и неинвертирующим усилителями.
Что такое инвертирующий и неинвертирующий усилитель?
Чтобы знать, что такое инвертирующие и неинвертирующие усилители, прежде всего, мы должны знать их определения, а также различия между ними.Разница между этими двумя в основном состоит в следующем.
Что такое инвертирующий усилитель?
В этом типе усилителя сигнал открытия сдвинут по фазе ровно на 180 градусов по отношению к входному сигналу. Когда напряжение + Ve приложено к цепи, то o / p схемы будет –Ve. Принципиальная схема инвертирующего усилителя представлена ниже.
инвертирующий усилительЕсли этот усилитель считается идеальным, мы должны применить концепцию виртуального короткого замыкания на клеммах i / p операционного усилителя.Таким образом, напряжение на двух клеммах эквивалентно.
Применить KCL (закон тока Кирхгофа) в инвертирующем узле схемы усилителя
(0-Vi) / Ri + (0-Vo) / Rf = 0
Упростив приведенные выше термины, мы получим следующее формула.
Коэффициент усиления по напряжению (Av) = Vo / Vi = –Rf / Ri
Коэффициент усиления инвертирующего усилителя составляет Av = –Rf / Ri
Что такое неинвертирующий усилитель?
В усилителях этого типа выход точно совпадает по фазе с входом.Когда к цепи приложено напряжение + Ve, то положительный сигнал будет положительным. O / p не инвертируется по фазе. Принципиальная схема неинвертирующего усилителя показана ниже.
неинвертирующий усилительКак только операционный усилитель считается идеальным, мы должны использовать концепцию виртуального короткого замыкания. Таким образом, напряжения на двух клеммах эквивалентны друг другу.
Примените KCL в инвертирующем узле в схеме
(Vi-Vo) / R2 + (Vo-0) / R1 = 0
Изменив приведенные выше термины, мы можем получить следующую формулу.
Av (усиление по напряжению) = Vo / Vi = (1 + Rf / Ri)
Коэффициент усиления неинвертирующего усилителя составляет Av = (1 + Rf / Ri)
Разница между инвертирующим и неинвертирующим -инвертирующий усилитель
Инвертирующий усилитель | Неинвертирующий усилитель |
| Тип обратной связи, используемой в этом усилителе, — это шунтирующая обратная связь по напряжению или отрицательная обратная связь. | В данном усилителе используется обратная связь последовательного типа или отрицательная обратная связь. |
| Входное и выходное напряжения этого усилителя синфазны. | Входные и выходные напряжения этого усилителя не совпадают по фазе. |
| Выход этого усилителя инвертирован. | Выход этого усилителя синфазен входному сигналу.
|
| В этом усилителе опорное напряжение может подаваться на инвертирующий вывод | В этом усилителе опорное напряжение может подаваться на неинвертирующий вывод |
| Коэффициент усиления этого усилителя Av = — Rf / Ri | Коэффициент усиления неинвертирующего усилителя Av = (1+ Rf / Ri). |
| Сопротивление i / p уменьшается из-за обратной связи –Ve. | Сопротивление i / p увеличивается из-за обратной связи –Ve. |
| Коэффициент усиления по напряжению этого усилителя может быть изменен, если он меньше, больше или равен 1 | Коэффициент усиления по напряжению этого усилителя> 1 |
| Импеданс i / p равен R1 | i / p сопротивление очень велико |
Часто задаваемые вопросы
1). Что такое инвертирующий и неинвертирующий усилитель?
Усилитель, у которого выходной сигнал сдвинут по фазе на 180 градусов по отношению к входу, известен как инвертированный усилитель, тогда как усилитель, у которого есть фаза o / p относительно i / p, известен как неинвертирующий усилитель.
2). Какова функция инвертирующего усилителя?
Этот усилитель используется для удовлетворения критериев Баркгаузена в схемах генератора для генерации устойчивых колебаний.
3). Для чего используются неинвертирующие усилители?
Неинвертирующие усилители в основном используются там, где требуется высокий импеданс i / p.
4). Какова функция неинвертирующего усилителя?
Используется для обеспечения высокого входного сопротивления
5).Какая обратная связь используется в инвертирующем усилителе?
Этот усилитель использует обратную связь -Ve для точного управления усилением усилителя, однако вызывает падение усиления в усилителях.
6). Что такое инвертирующий вход?
Операционный усилитель имеет три клеммы, например, два входа и один выход, причем один из входов известен как инвертирующий вход и отмечен знаком минус (-)
7). Какое усиление по напряжению у инвертирующего усилителя?
Коэффициент усиления напряжения (A) = Vout / Vin = — Rf / Rin
8).Каков коэффициент усиления по напряжению неинвертирующего усилителя?
Коэффициент усиления напряжения (A) = Vout / Vin = (1+ Rf / Rin)
9). Как влияет отрицательная обратная связь на неинвертирующий усилитель?
- Входное сопротивление будет увеличено, а выходное сопротивление уменьшено.
- Полоса пропускания будет увеличена
- Выходной шум усилителя будет уменьшен
- Воздействие шума будет уменьшено.
Таким образом, в этом вся разница между инвертирующим усилителем и неинвертирующим усилителем .
