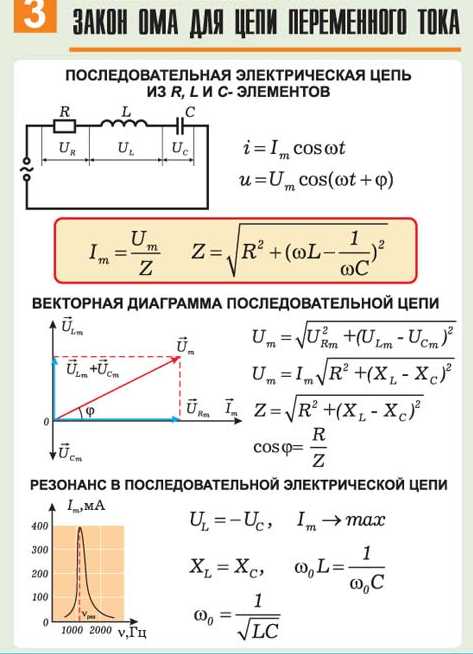
Что представляет собой цепь переменного тока с R, L и C элементами. Как рассчитать полное сопротивление такой цепи. Какие процессы происходят при прохождении тока через активное, индуктивное и емкостное сопротивления. Как построить векторную диаграмму напряжений и токов для цепи с R, L и C. Что такое резонанс напряжений и при каких условиях он возникает.
Структура и компоненты цепи переменного тока с R, L и C
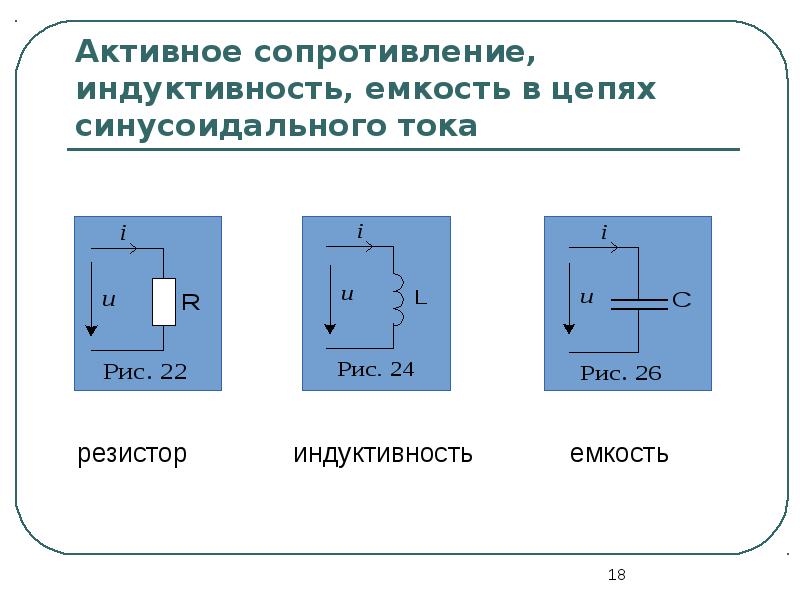
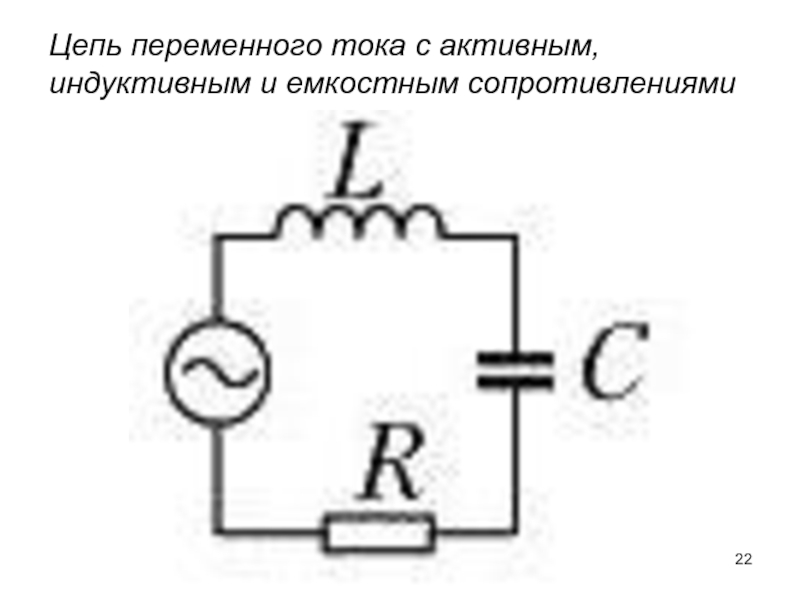
Цепь переменного тока с активным сопротивлением, индуктивностью и емкостью представляет собой последовательное соединение трех основных элементов:
- Резистор R — активное сопротивление
- Катушка индуктивности L
- Конденсатор C
Такая цепь является обобщенным случаем и позволяет изучить все основные процессы, происходящие в цепях переменного тока. Рассмотрим подробнее характеристики каждого элемента.
Резистор R — активное сопротивление
Резистор обладает активным сопротивлением R, на котором происходит необратимое преобразование электрической энергии в тепловую. Напряжение и ток на резисторе совпадают по фазе:

- uR = i * R
- φR = 0
Катушка индуктивности L
Индуктивность создает реактивное индуктивное сопротивление XL. Напряжение на катушке опережает ток на 90°:
- XL = ωL = 2πfL
- uL = i * XL
- φL = +90°
Конденсатор C
Емкость создает реактивное емкостное сопротивление XC. Напряжение на конденсаторе отстает от тока на 90°:
- XC = 1 / (ωC) = 1 / (2πfC)
- uC = i * XC
- φC = -90°
Расчет полного сопротивления цепи переменного тока
Полное сопротивление цепи Z, называемое также импедансом, рассчитывается по формуле:
Z = √(R2 + (XL — XC)2)
Где:
- R — активное сопротивление
- XL — индуктивное сопротивление
- XC — емкостное сопротивление
Разность XL — XC называется реактивным сопротивлением цепи X:
X = XL — XC = ωL — 1/(ωC)
Таким образом, полное сопротивление можно выразить через активное и реактивное:
Z = √(R2 + X2)
Векторная диаграмма напряжений и токов
Для анализа фазовых соотношений между током и напряжениями на элементах цепи удобно использовать векторную диаграмму. Порядок построения:
- Вектор тока I направляем по действительной оси
- Вектор UR совпадает по направлению с током
- Вектор UL опережает ток на 90°
- Вектор UC отстает от тока на 90°
- Вектор полного напряжения U получается сложением UR, UL и UC
Угол φ между векторами U и I определяет сдвиг фаз между напряжением и током в цепи:
tg φ = (XL — XC) / R = X / R
Мощность в цепи переменного тока
В цепи переменного тока различают следующие виды мощности:
Активная мощность P
Характеризует скорость преобразования электрической энергии в другие виды:
P = I2R = U2/R = UI cos φ
Реактивная мощность Q
Характеризует амплитуду колебаний энергии между источником и реактивными элементами:
Q = I2X = U2/X = UI sin φ
Полная мощность S
Определяет полную нагрузку цепи:
S = UI = √(P2 + Q2)
Резонанс напряжений в цепи с R, L и C
Резонанс напряжений — это режим работы цепи, при котором напряжение на индуктивности равно напряжению на емкости:
UL = UC
Условие резонанса:
XL = XC или ωL = 1/(ωC)
Резонансная частота:
ω0 = 1/√(LC)
При резонансе:
- Реактивное сопротивление X = 0
- Полное сопротивление Z = R
- Ток максимален I = U/R
- Угол сдвига фаз φ = 0
Особенности цепи переменного тока с R, L и C
Основные особенности цепи переменного тока с последовательным соединением активного сопротивления, индуктивности и емкости:
- Полное сопротивление цепи зависит от частоты тока
- Между напряжением и током существует сдвиг по фазе
- Напряжения на реактивных элементах могут превышать напряжение источника
- Возможен резонанс напряжений при определенной частоте
- Активная мощность выделяется только на активном сопротивлении
- Реактивная мощность колеблется между индуктивностью и емкостью
Применение цепей переменного тока с R, L и C
Цепи с последовательным соединением R, L и C находят широкое применение в электротехнике и электронике:
- Частотные фильтры для выделения или подавления определенных частот
- Резонансные контуры в радиоприемниках и передатчиках
- Компенсация реактивной мощности в электрических сетях
- Цепи коррекции частотных характеристик усилителей
- Генераторы синусоидальных колебаний
Понимание процессов в таких цепях важно для анализа и проектирования различных электротехнических устройств.
Методы расчета цепей переменного тока
Для анализа цепей переменного тока с R, L и C элементами применяются различные методы расчета:
Метод комплексных амплитуд
Основан на представлении синусоидальных величин в виде комплексных чисел. Позволяет применять методы расчета цепей постоянного тока к цепям переменного тока.
Символический метод
Использует алгебраическую форму записи комплексных чисел. Удобен для расчетов с применением правил Кирхгофа.
Метод векторных диаграмм
Позволяет наглядно представить соотношения между токами и напряжениями. Эффективен для простых цепей.
Топографический метод
Основан на построении векторной диаграммы потенциалов узлов схемы. Применяется для сложных разветвленных цепей.

Выбор метода зависит от сложности схемы и требуемой точности расчетов. Для простых цепей часто достаточно применения закона Ома в комплексной форме.
Влияние частоты на параметры цепи
Частота переменного тока оказывает существенное влияние на характеристики цепи с R, L и C элементами:
- С ростом частоты увеличивается индуктивное сопротивление XL = ωL
- При повышении частоты уменьшается емкостное сопротивление XC = 1/(ωC)
- Изменение реактивных сопротивлений влияет на полное сопротивление цепи Z
- От частоты зависит угол сдвига фаз φ между током и напряжением
- При определенной частоте наступает резонанс напряжений
Учет частотных зависимостей важен при проектировании и эксплуатации устройств переменного тока.
Цепь с активным сопротивлением — Знаешь как
Содержание статьи
Напряжение и ток
Цепь, изображенная на рис. 5-17, обладает активным сопротивлением г и индуктивностью L. Примером такой цепи может служить катушка любого электромагнитного прибора или аппарата.
При прохождении переменного тока i в цепи будет индуктироваться э. д. с. самоиндукции eL.
Согласно второму правилу Кирхгофа u + eL = ir
откуда напряжение на зажимах цепи
и = it — eL = ir + L (di/dt)= ua + u
Первая слагающая uа = ir называется активным напряжением, мгновенное значение которого пропорционально току, а вторая uL = — eL = L(di/dt) реактивным напряжение м, мгновенное значение которого пропорционально скорости изменения тока.
Если ток изменяется по закону синуса
i — I
м sin ωtто активное напряжение
uа = ir = Iмr sin ωt = Uа м sin ωt
Рис. 5-17, Цепь с активным сопротивлением и индуктивностью.
Оно изменяется также синусоидально, совпадая по фазе с током.
Амплитудное значение активного напряжения
Uа м = Iмr,
а действующее значение
Uа = Ir,
Реактивное напряжение
uL = L di/dt = ωLIM cos ωt = ULм sin(ωt + π/2)
Оно изменяется синусоидально, опережая по фазе ток на 90°.
Амплитудное значение реактивного напряжения
ULм = ωLI
 а действующее значение
а действующее значение
UL = ωLI = xLI
Напряжение на зажимах цепи
и= иa + uL = Uа м sin ωt + ULM sin (ωt + π/2) = UMsin (ωt + φ).
Напряжение на зажимах изменяется синусоидально, опережая ток по фазе на угол φ.
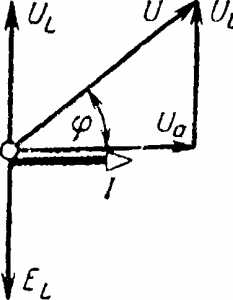
На рис. 5-18 показаны графики; i, иa, uL и и, а на рис. 5-19 — векторная диаграмма цепи. На диаграмме векторы напряжений U, Ua и UL образуют прямоугольный треугольник напряжений, из которого непосредственно следует соотношение, связывающее эти величины:
U=√(U2a + U2L ) .
Аналогичная зависимость имеет место и для амплитудных значений
Угол сдвига фаз между напряжением на зажимах
Рис 5-18. Графики тока и напряжения в цепи с активным сопротивлением и индуктивностью.
Рис 5-19. Векторная диаграмма цепи с активным сопротивлением и индуктивностью.
цепи и током в ней находится из треугольника напряжений по одной из формул
cos φ = Ua/U и tg φ = UL/Ua
 Чем больше реактивное напряжение по сравнению с активным, тем на больший угол ток отстает по фазе от напряжения на зажимах цепи.
Чем больше реактивное напряжение по сравнению с активным, тем на больший угол ток отстает по фазе от напряжения на зажимах цепи.
Сопротивления цепи
Уравнение (5-30) можно переписать в следующем виде
U = √(Ir)2 + (IxL)2 = I√r2 + x2L
откуда ток в цепи
I = U/z = U / √(r2 + x2L)
Величина
z = √(r2 + x2L) = √(r2 + ωL)2
называется полным сопротивлением цепи.
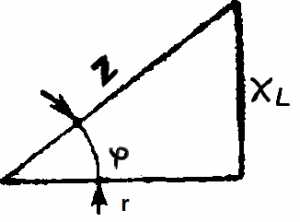
Сопротивления r, xL и z графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20), который можно получить из треугольника напряжений, уменьшив каждую из его сторон в I раз.
Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z и r, можно определить через
cos φ = Ua /U
Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью
Мощности
Мгновенное значение мощности р = ui = Uм sin (ωt + φ) Iм sin ωt = UмIм sin (ωt + φ) sin ωt Учитывая, что
sin (со/ + φ) sin ωt = 1/2 cos φ — 1/2 cos (2ωt + φ)
а также (5-28), можно написать другое выражение ной мощности
Р = UI cos φ — UI cos (2ωt + φ)
Написанное выражение состоит из двух членов: постоянного, независимого от времени UI cos φ и переменного си-
нусоидального UI cos (2ωt + φ). Среднее значение мощности за период, которым обычно пользуются при расчете цепей переменного тока, будет равно постоянному члену UI cos φ, так как среднее значение за период синусоидальной функции равно нулю.
Таким образом, среднее значение мощности цепи равно произведению действующих значений напряжения и тока, умноженному на cos φ, т.е.
P = UI cos φ.
Так как U cos φ = U r/z = Ir = Ua,
то
P = UаI = I2r
Следовательно, средняя мощность цепи равна среднему значению мощности в активном сопротивлении. Поэтому среднюю мощность любой цепи называют; еще и активной мощностью.

Реактивная мощность цепи:
Q = ULI= I2xL = I2z sin φ = UI sin φ
т.е. реактивная мощность цепи равна произведению действующих значений напряжения и тока, умножен ному на sin φ.
Рис.5-21. Треугольник мощностей
Полной мощностью цепи называется произведение действующих значений напряжения и тока, т. е.
S = UI
Учитывая, что sin2 φ + cos2 φ = 1 можно написать: (UI cos φ)2 + (UI sin φ)2 = (UI)2
или, что то же,
P2 + Q2 = S2,
следовательно,
S = √(P2 + Q2)
Мощности Р, Q и S графически можно изобразить сторонами прямоугольного треугольника — треугольника мощностей (рис 5-21), который можно получить из треугольника напряжений, умножая на I все его стороны.
т.е отношение активной мощности к полной называется коэффициентом мощности.
Единица полной мощности с называется вольт-ампер (в •а).
Необходимость применения понятия полной мощности обусловлена тем, что конструкция, габариты, вес и стоимость машины или аппарата определяются их номинальной полной мощностью Sн = UнIн а полная мощность S при том или ином режиме работы их определяет степень их использования.
Статья на тему Цепь с активным сопротивлением
znaesh-kak.com
3.4.7. Цепь с активным сопротивлением, индуктивностью и емкостью
Цепь с активным сопротивлением, индуктивностью и емкость, представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 51).
Рис. 51 Рис. 52 Рис. 53
Снова принимаем фазу тока нулевой: . Тогда напряжение на активном сопротивлениинапряжение на индуктивностинапряжение на емкости. Построим векторную диаграмму при условии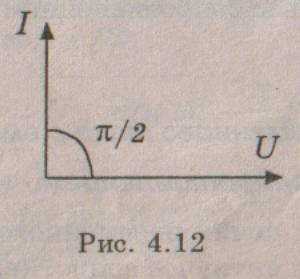 т. е..
т. е..
Вектор
результирующего напряжения
 замыкает многоугольник векторов
замыкает многоугольник векторов ,
, и
и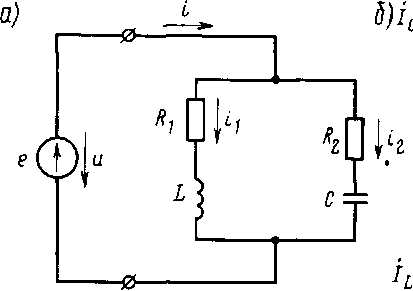 (рис. 52). Вектор
(рис. 52). Вектор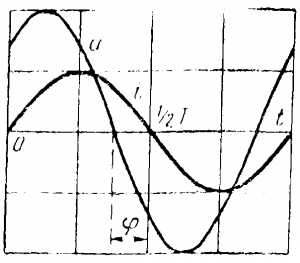 +
+
определяет напряжение на индуктивности
и емкости. Как видно из диаграммы это
напряжение может быть меньше напряжения
на каждом из участков в отдельности.
Это объясняется процессом обмена
энергией между индуктивностью и емкостью.
Выведем закон Ома для рассматриваемой
цепи. Так как модуль вектора
определяет напряжение на индуктивности
и емкости. Как видно из диаграммы это
напряжение может быть меньше напряжения
на каждом из участков в отдельности.
Это объясняется процессом обмена
энергией между индуктивностью и емкостью.
Выведем закон Ома для рассматриваемой
цепи. Так как модуль вектора
 +
+ определяют как разность действующих
значений
определяют как разность действующих
значений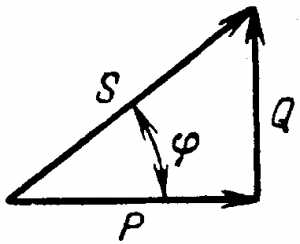
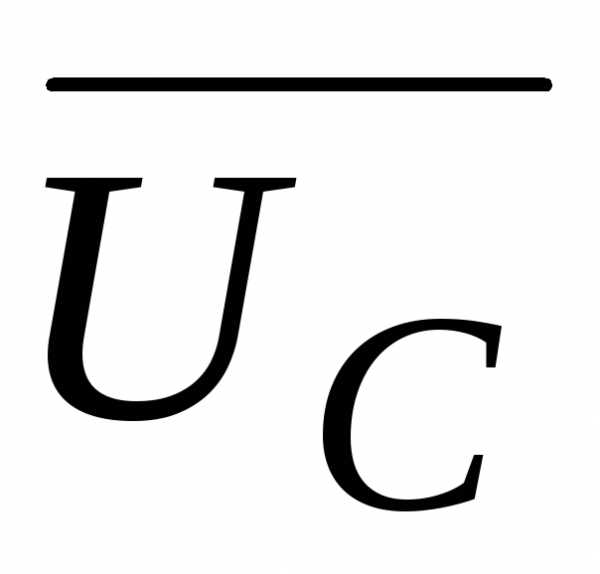 ,
из диаграммы рис. 52 ,что.
,
из диаграммы рис. 52 ,что.
Но
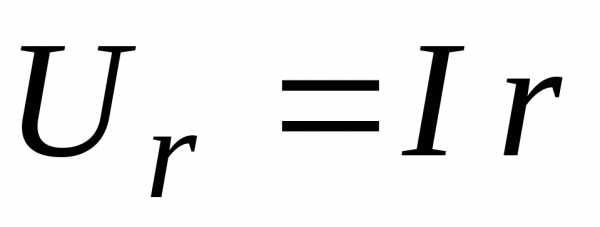 ;
;
,
следовательно,
;
;
,
следовательно,
,
откуда
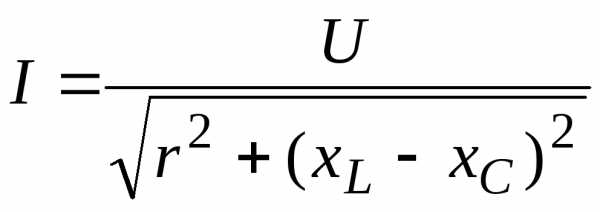 .
(3.37)
.
(3.37)
Вводя обозначения , гдеz — полное сопротивление цепи, получим
. (3.38)
Разность
между индуктивным и емкостным
сопротивлениями
называют реактивным сопротивлением
цепи. Учитывая это, получим треугольник
сопротивлений для цепи сr,
L
и С
(рис.53). При
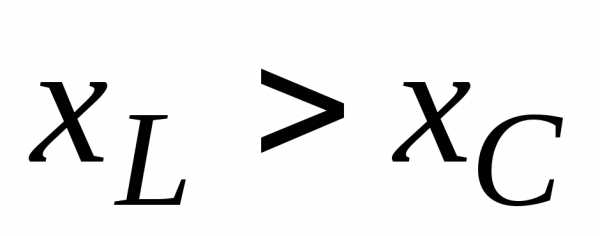 реактивное сопротивление положительно
и сопротивление цепи носит
активно-индуктивный характер.
реактивное сопротивление положительно
и сопротивление цепи носит
активно-индуктивный характер.
При
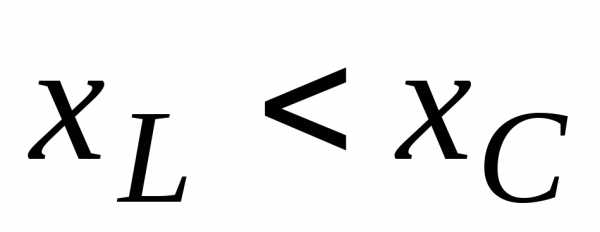 реактивное сопротивление отрицательно
и сопротивление цепи носит активно-емкостный
характер. Знак угла сдвига фаз между
током и напряжением получаем автоматически,
так как реактивное сопротивление —
величина алгебраическая:
реактивное сопротивление отрицательно
и сопротивление цепи носит активно-емкостный
характер. Знак угла сдвига фаз между
током и напряжением получаем автоматически,
так как реактивное сопротивление —
величина алгебраическая:
. (3.39)
Таким
образом, при
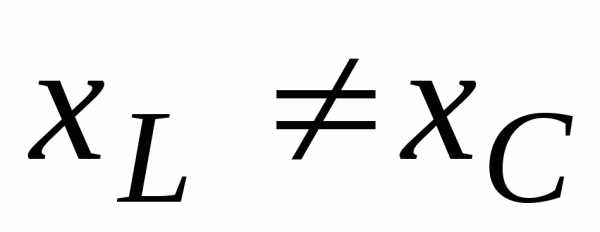 преобладает или индуктивное, или
емкостное сопротивление, т, е. с
энергетической точки зрения цепь сr,
L
и С
сводится к цепи с r,
L
или с с r,
С. Тогда
мгновенное значение мощности
преобладает или индуктивное, или
емкостное сопротивление, т, е. с
энергетической точки зрения цепь сr,
L
и С
сводится к цепи с r,
L
или с с r,
С. Тогда
мгновенное значение мощности
,
причем знак φ определяется по формуле (3.39). Соответственно активная, реактивная и полная мощности определяются выражениями.
; ..
3.4.8. Резонанс напряжений
Резонансом напряжения называется явление в цепи с последовательным колебательным контуром, когда ток в цепи совпадает по фазе с напряжением источника.
На рис.54 показана схема последовательного колебательного контура.
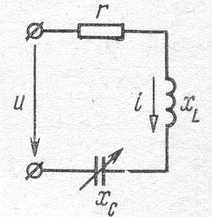
Рис. 54
Найдем условие резонанса напряжений. Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление к цепи должно равняться нулю, так как .
Таким
образом, условием резонанса напряжений
является х
= 0 или
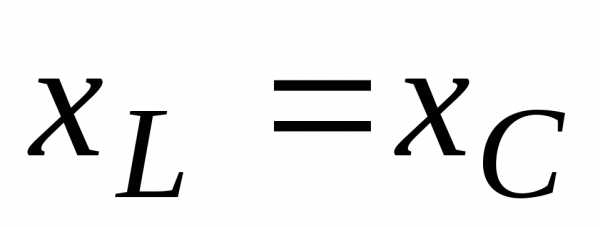 .
Но
,
а,
гдеf
— частота источника питания.
.
Но
,
а,
гдеf
— частота источника питания.
В результате можно записать
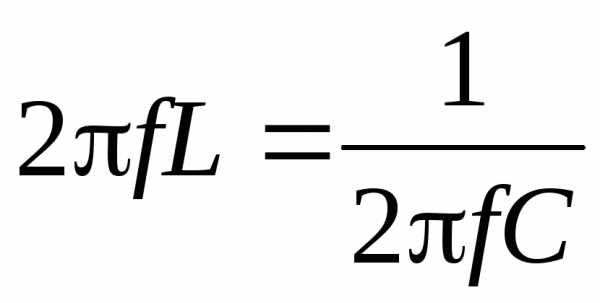 .
.
Решая это уравнение относительно f , находим
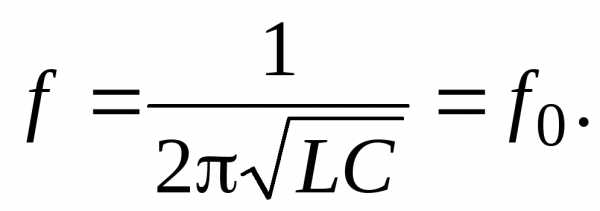 (3.40)
(3.40)
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Выражение
(3.40) является формулой Томсона, определяющей
зависимость собственной частоты
колебаний контура
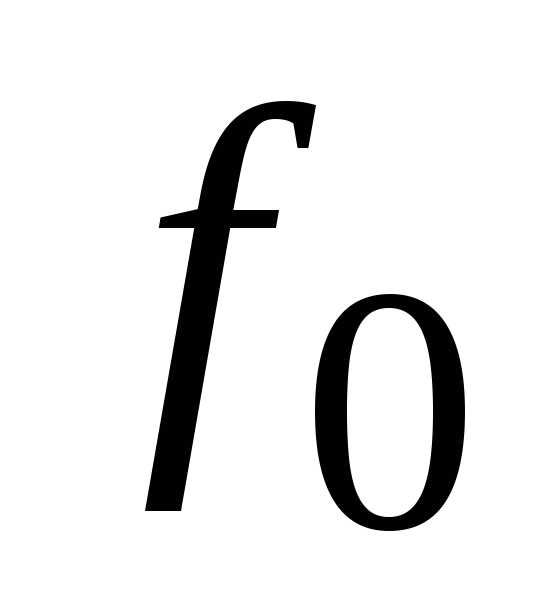 ,
от параметровL
и С.
Следует вспомнить, что если конденсатор
контура зарядить от источника
постоянного тока, а затем замкнуть его
на индуктивную катушку, то в контуре
возникнет переменный ток частоты
,
от параметровL
и С.
Следует вспомнить, что если конденсатор
контура зарядить от источника
постоянного тока, а затем замкнуть его
на индуктивную катушку, то в контуре
возникнет переменный ток частоты
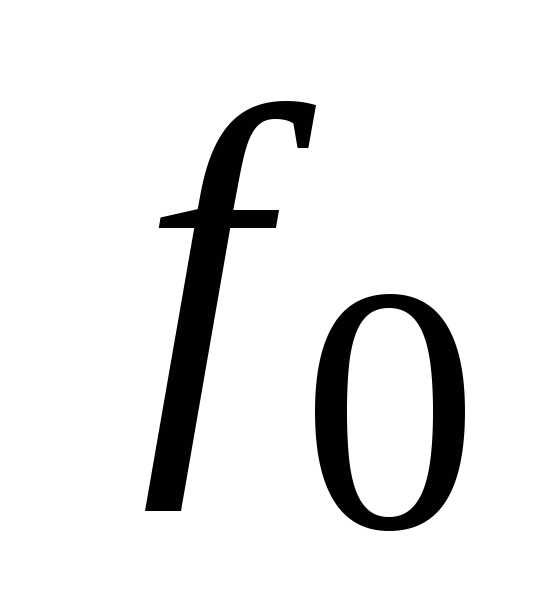 .
Вследствие потерь колебания в контуре
будут затухать, причем время затухания
зависит от величины потерь.
.
Вследствие потерь колебания в контуре
будут затухать, причем время затухания
зависит от величины потерь.
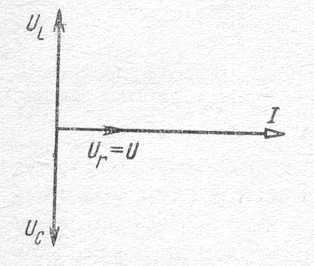
Рис. 55
Резонансу напряжений соответствует векторная диаграмма, приведенная на рис.55. На основании этой диаграммы и закона Ома для цепи с r, L и С сформулируем признаки резонанса напряжений:
а)
сопротивление всей цепи
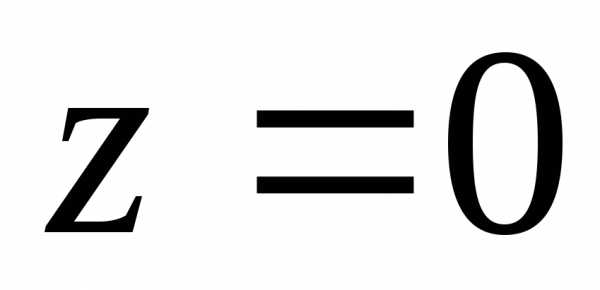 минимальное и чисто активное;
минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
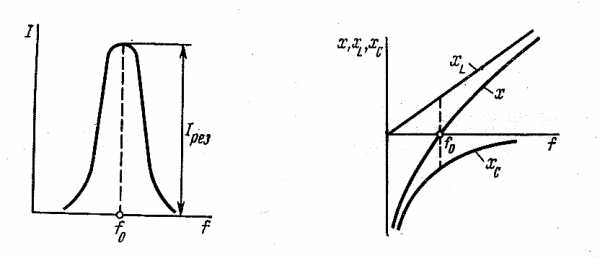
Рис. 56 Рис. 57
в) напряжение на индуктивной катушке равно напряжению на емкости и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряжение на индуктивности и емкости обусловлено накопленной в них энергией, величина которой тем больше, чем меньше потери в цепи. Количественно указанное явление характеризуется добротностью контура Q, которая представляет собой отношение напряжения на катушке или емкости к напряжению на зажимах цепи при резонансе;
. (3.41)
При резонансе Величина называется волновым сопротивлением контура. Таким образом,
(3.42)
Способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот характеризуется резонансной кривой (рис. 56).
Резонансная кривая показывает зависимость действующего значения тока в контуре от частоты источника при неизменной собственной частоте контура.
Эта зависимость определяется законом Ома для цепи с r, L и С. Действительно, I = U/z, где
(3.43)
На
рис. 57 показана зависимость реактивного
сопротивления
от частоты источника. Анализ этого
графика и выражения (3.43) показывает, что
при низких и высоких частотах реактивное
сопротивление велико и ток в контуре
мал. При частотах, близких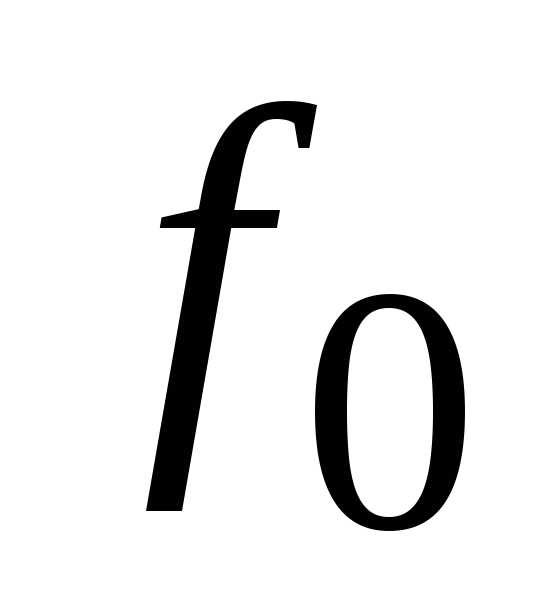 реактивное сопротивление мало и ток
контура велик. При этом, чем больше
добротность контураQ
, тем острее
резонансная кривая контура.
реактивное сопротивление мало и ток
контура велик. При этом, чем больше
добротность контураQ
, тем острее
резонансная кривая контура.
studfiles.net
1.2. Цепь с активным сопротивлением и емкостью
Методика изучения цепи с R и С (рис. 4,а) аналогична методике изучения цепи с R и L. Задаемся током . Тогда напряжение на активном сопротивлении. Напряжение на емкости отстает по фазе от тока на уголπ/2: . На основании приведенных выражений построим векторную диаграмму для этой цепи (рис. 4,б).
а) б) в)
Рис. 4. К анализу цепи с последовательным соединением R и С
Закон Ома для цепи с R и С.
где – полное сопротивление цепи.
Треугольник сопротивлений для рассматриваемой цепи показан на рис. 4, в. Расположение его сторон соответствует расположению сторон треугольника напряжений на векторной диаграмме рис. 3,б. Сдвиг фаз φ в этом случае отрицателен, так как напряжение отстает по фазе от тока:
;
Мощности:
.
Реактивная мощность характеризует интенсивность обмена энергией между емкостью и источником .
Так как φ<0, то реактивная мощность Q<0. Физически это означает, что когда емкость отдает энергию, то индуктивность ее потребляет, если они находятся в одной цепи.
Треугольник мощностей для данной цепи приведен на рис. 6.
Рис. 6. Треугольник мощностей для цепи с R и С
1.3. Цепь с активным сопротивлением, индуктивностью и емкостью
Цепь с R, L и С представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 5,а). Принимаем фазу тока нулевой: .
а) б) в)
Рис. 5. Схема цепи переменного тока с R и L,
ее векторная диаграмма, треугольник сопротивлений
Тогда напряжение на активном сопротивлении , напряжение на индуктивности , напряжение на емкости. Построим векторную диаграмму при условииXL> Хс, т.е. UL = IXL> UC = IXC.
Вектор результирующего напряжения U замыкает многоугольник векторов UR, UL и UС (рис. 5,б). Вектор UL + Uc определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессом обмена энергией между индуктивностью и емкостью.
Закон Ома для цепи с R, L и С.
где – полное сопротивление цепи;
–реактивное сопротивление цепи, Ом.
При XL> Xc реактивное сопротивление положительно и сопротивление цепи носит активно-индуктивный характер, при XL< Xc реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостной характер.
Таким образом, при XL≠XC преобладает или индуктивное, или емкостное сопротивление, т. е. с энергетической точки зрения цепь с R, L и С сводится к цепи с R, L или с R, С.
Мощности:
Знак сдвига фаз φ определяется по формуле
Ответьте на следующий вопрос:
Полное сопротивление Z приведенной цепи при Ом иОм составляет…
50 Ом
100 Ом
400 В
50 Гц
Вывод по первому вопросу: процессы, протекающие в однофазных цепях переменного тока со смешанным последовательным соединением приемников, характеризуются появлением понятий полного сопротивления, полной мощности, треугольников сопротивлений и мощностей, повторяющих треугольник напряжений. В них также необходимо учитывать взаимные фазовые сдвиги напряжений и токов. Умение анализировать однофазные цепи со смешанным соединением резисторов является важным при изучении трехфазных цепей, принципа действия и устройства электрических машин.
studfiles.net
31. Цепь тока с активным сопротивлением.
Цепь переменного тока, содержащая омическое сопротивление R, не представляет особенностей. В ней выполняется закон Ома, который может быть применен как к мгновенным, так и эффективным значениям напряжения и тока: .
Сопротивление R в цепи переменного тока называется активным, так как при прохождении тока в нем происходит необратимая потеря энергии, которая переходит в теплоту.
Колебания напряжения и тока в цепи с чисто активным сопротивлением находятся в фазе.
32. Цепь с индуктивным сопротивлением.
Рассмотрим явления, происходящие в цепи переменного тока с индуктивностью. Подключим к переменному напряжению U = Um sint катушку с индуктивностью «L«, активным сопротивлением которой за малостью можно пренебречь.
В цепи образуется переменный ток и в катушке возникает э.д.с. самоиндукции, равная. Сила тока «I» в цепи определяется из условия: ,(так как сопротивлением «R» пренебрегаем) или .
Преобразуем или.
Интегрируем это уравнение
, где .
Постоянная интегрирования принимается С = 0, так как не имеет постоянной составляющей. Уравнение показывает, что ток в цепи, подобно напряжению, имеет синусоидальный характер, но по фазе запаздывает на угол .Сопоставляя максимальное значение токас формулой закона Ома, видим, что в цепи с индуктивностью значение сопротивления имеет величина «L«, которая обозначается XL..Величина XL = L = 2L называется индуктивным сопротивлением цепи и измеряется в Омах, при подстановке L — в Генри и — в Герцах.Физический смысл индуктивного сопротивления состоит в том, что оно учитывает влияние на силу тока в цепи э.д.с. самоиндукции, противодействующей приложенному напряжению, и поэтому зависит от тех же величин, что и э.д.с. самоиндукции: индуктивности «L» и частоты = 2, обусловливающей скорость изменения мгновенных значений тока.Э.д.с. самоиндукции, противодействующая изменению тока в цепи, вызывает запаздывание колебаний тока, по отношению к колебаниям напряжения. При чисто индуктивной цепи запаздывание происходит на угол, равный .Графики напряжения и тока в цепи с индуктивностью показаны на рисунке. На векторной диаграмме показано фазовое соотношение векторов амплитуд токаIL и напряжения UL: ток отстает на угол (углы отсчитываются по направлению против часовой стрелки).В цепи, содержащей индуктивное и активное сопротивление, угол запаздывания тока по фазе будет меньше и в зависимости от соотношения между ними может иметь значения в пределах от 0 до.В чисто индуктивном сопротивлении потерь энергии не происходит, в связи с чем оно называется реактивным.
33. Цепь с емкостным сопротивлением.
Определим характер переменного тока «I» в цепи с конденсатором, к которой приложено переменное напряжение U = Um sint.
Мгновенные значения заряда «q» на пластинах конденсатора
q = cU = cUm sin t.
Дифференцируем
где Im = cUm. Это уравнение показывает, что ток в цепи, подобно напряжению, имеет синусоидальный характер (смотри рисунок), причем упреждает напряжение по фазе на угол.Сопоставляя максимальное значение токаIm = cUmс формулой закона Ома, видим, что в цепи с емкостью значение сопротивления имеет величина , которая обозначаетсяXc.Величина называется емкостным сопротивлением цепи и измеряется в Омах, еслис — в Фарадах и — в Герцах. Физический смысл емкостного сопротивления можно объяснить так: ток «I» в цепи конденсатора пропорционален заряду «q» и частоте «» смены процессов заряда и разряда конденсатора. Заряд «q» при данном приложенном напряжении «U» пропорционален емкости «с» конденсатора, а = 2. Поэтому ток «I» в цепи пропорционален произведению «c«, которое, следовательно, имеет значение проводимости цепи. Величина, ей обратная, то есть , имеет значение сопротивления цепи.В цепи, содержащей емкость и активное сопротивление, угол сдвига фазы тока будет меньше и в зависимости от соотношения между ними может иметь значения от 0 до 900.В чисто емкостном сопротивлении потерь энергии не происходит, в связи с чем оно называется реактивным.
34. Полное сопротивление цепи переменного эл.тока. Импеданс. . Рассм. цепь, состю из последю соед-ных резистора R, катушки индук-тивности L и конденсатора С. Если на нее подать перемен. напряж-е , то ток в цепи будет изм-ся по закону: ,где- разность фаз напр-я и силы тока. Такая цепь им. как актив., так и реактивное сопр-я. => ее сопр-е наз. импедансом и обозначаютZ. Импеданс равен отношению амплитуд. значения переем. напр-я на концах цепи к амплитуд. Знач-ю силы тока в ней:
Элементы(R,L,С)полной цепи перем. тока на рис. соединены последо-вательно. => по ним протекает одинак. ток, а напрсклад-ся из напр-ний на отдел. участках цепи:Для сложения напр-ний исп. след. графич. прием. На вектор.диаграмме отклад-сякак векторы все 3 ампл-ды напр-ний Тогда сумма этих векторов дает вектор напряж-я в цепи. Вел-на и направл-е вектора дают амплитуду напр-ния в сети и фазовый угол между током и напряжением. Из рис. по т. Пифагора имеем: Подставляя выражения этих амплитуд из и учит. закон Ома, находим:Дальше пол. выр-е для определения импеданса:
studfiles.net
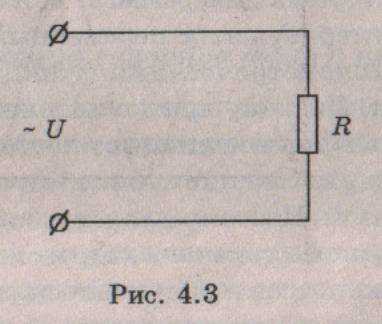
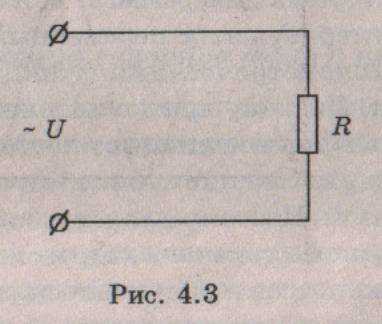
Цепь переменного тока с активным сопротивлением Рассмотрим цепь (рис, 4,3), в которой к активному сопротивлению (резистору) приложено синусоидальнее напряжение
Цепь переменного тока с активным сопротивлением
Рассмотрим
цепь (рис, 4,3), в которой к активному
сопротивлению (резистору) приложено
синусоидальнее напряжение:
(4.6)
Тогда
по закону Ома ток в цепи будет
равен:
(4.7)
Мы
видим, что ток и напряжение совпадают
по фазе. Векторная диаграмма для этой
цепи приведна на рис. 4.4, а зависимости
тока и напряжения от времени (временная
диаграмма) — на рис. 4.5:
Выясним,
как изменяется со временем мощность в
цепи переменного тока с резистором.
Мгновенное
значение мощности равно произведению
мгновенных значений тока и напряжения:
(4.8)
Из
этой формулы мы видим, что мгновенная
мощность всегда положительна и пульсирует
с удвоенной частотой (рис 4.5).
I,U,p
Рис.
4.5
Это
означает, что электрическая энергия
необратимо превращается в теплоту
независимо от направления тока в цепи.
Те
элементы цепи, на которых происходит
необратимое преобразование электрической
энергии в другие виды энергии (не только
в теплоту), называются активными
сопротивлениями.
Поэтому резистор представляет собой
активное сопротивление.
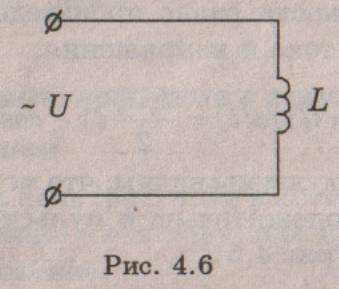
Цепь переменного тока с индуктивностью
Рассмотрим цепь (рис. 4.6), в которой к катушке индуктивности L, не обладающей активным сопротивлением (R = 0), приложено синусоидальное напряжение (4.6).
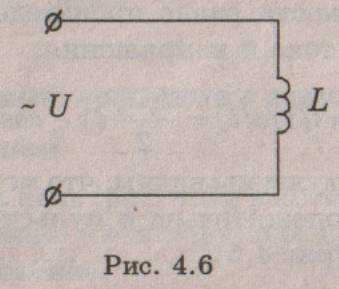
Протекающий
через катушку переменный ток создает
в ней ЭДС самоиндукции
,
которая в cооветствии с правилом Ленца
направлена таким образом, что препятствует
изменению тока. Другими словами, ЭДС
самоиндукции направлена навстречу
приложенному напряжению. Тогда в
соответствии со вторым правилом Кирхгофа
можно записать:
(4.9)
Согласно
закону Фарадея ЭДС самоиндукции
(4.10)
Подставив
(4.10) в (4.9), получим:
Решение
этого дифференциального уравнения
имеет вид:
(4.12)
где
(4.13)
Деля
обе части равенства (4.13) на
,
получим для действующих значений
(4.14)
Соотношение
(4.14) представляет собой закон Ома для
цепи с идеальной индуктивностью, а
величина
называется
индуктивным
сопротивлением.
Индуктивное сопротивление измеряется
в омах.
Из
формулы (4.12) мы видим, что в рассмотренной
цепи ток отстает по фазе от напряжения
на ?
/ 2.
Векторная диаграмма для этой цепи
изображена на
рис.
4.7, а временная — на рис. 4.8.
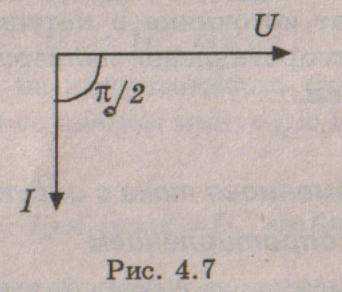
Мгновенная
мощность в цепи с чисто индуктивным
сопротивлением равна:
(4.15)
Мы видим,
она изменяется по закону синуса с
удвоенной частотой (рис. 4.8).
Положительные
значения мощности соответствуют
потреблению энергии катушкой, а
отрицательные — возврату запасенной
энергии обратно источнику. Средняя за
период мощность равна нулю. Следовательно,
цепь с индуктивностью мощности не
потребляет — это чисто реактивная
нагрузка. В этой цепи происходит лишь
перекачивание электриче
I,U,p
Рис.
4.8
кой
энергии от источника в катушку и обратно.
Индуктивное сопротивление является
реактивным сопротивлением.
Цепь переменного тока с индуктивностью и активным сопротивлением
Реальные
цепи, содержащие индуктивность, всегда
имеют и активное сопротивление:
сопротивление провода обмотки и
подводящих проводов. По
этому
рассмотрим электрическую цепь (рис.
4.9), в которой через катушку индуктивности
L,
обладающую активным сопротивлением R,
протекает переменный ток
(4.16)
Через
катушку и резистор протекает один и же
ток, поэтому в качестве основного выберем
век-
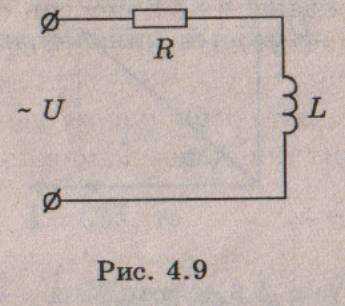
Рис.4.9
тор
тока и будем строить вектор напряжения,
приложенного к этой цепи.
Напряжение,
приложенное к цепи, равно векторной
сумме падений напряжений на катушке
индуктивности и на резисторе:
(4.17)
Напряжение
на резисторе, как было показано выше,
будет совпадать по фазе с
током:
(4.18)
а
напряжение на индуктивности будет равно
ЭДС самоиндукции со знаком минус (по
второму правилу Кирхгофа):
.
(4.19)
Мы
видим, что напряжение на индуктивности
опережает ток на угол ?/2. Построив векторы
и
,
и воспользовавшись формулой (4.17), найдем
вектор
Векторная
диаграмма показана на рис. 4.10. Мы видим,
что в рассматриваемой цепи ток I
отстает по фазе от приложенного напряжения
U, но не на ?
/ 2,
как в случае чистой индуктивности, а на
некоторый угол
.
Этот угол может принимать значения от
0 до ?
/ 2
и при заданной индуктивности зависит
от значения активного сопротивления:
с увеличением R угол уменьшается
I
Рис.4.10
Как
видно из векторной диаграммы, модуль
вектора
равен
,
(4.20)
где
величина
(4.21)
называется
полным сопротивлением цепи.
Сдвиг
по фазе
между
током и напряжением данной цепи также
определяется из векторной
диаграммы:
(4.22)
Цепь переменного тока с емкостью
Рассмотрим
электрическую цепь, в которой переменное
напряжение (4.6) приложено к емкости С
(рис.
4.11).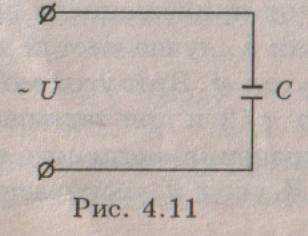
Мгновенное
значение тока в цепи с емкостью равно
скорости изменения заряда на обкладках
конденсатора:
(4.23)
но
поскольку q = СU,
то
(4.24)
где
(4.25)
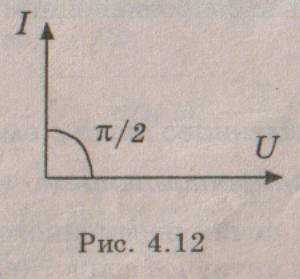
Мы
видим, что в этой цепи ток опережает
напряжение на ?/2.
Переходя в формуле (4.25) к действующим
значениям
переменного тока
)
получим:
(4.26)
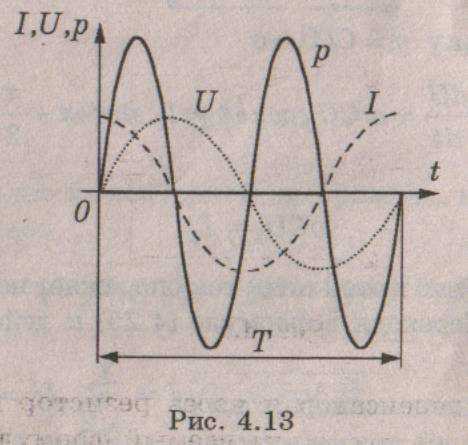
Это закон Ома для цепи переменного тока с емкостью, а величина — называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 4.12, а временная – на рис. 4.13
Мгновенная
мощность в цепи, содержащей емкость:
(4.27)
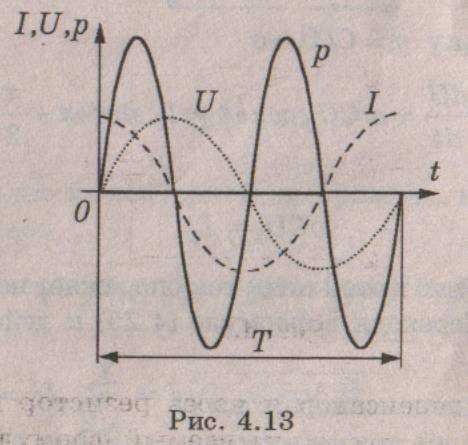
Мы
видим, что мгновенная мощность изменяется
с удвоенной частотой (рис. 4.13). При этом
положительные значения мощности
соответствуют заряду конденсатора, а
отрицательные — его разряду и возврату
запасенной энергии в источник. Средняя
за период мощность здесь равна нулю,
поскольку в цепи с конденсатором активная
мощность не потребляется, а происходит
обмен электрической энергией между
конденсатором и источником. Следовательно,
конденсатор так же, как и индуктивность,
является реактивным сопротивлением.
Цепь переменного тока с емкостью в активным сопротивлением
В реальных
цепях переменного тока с емкостью всегда
имеется активное сопротивление —
сопротивление проводов, активные потери
в конденсаторе и
т.д.
Поэтому реальную цепь с емкостью следует
рассматривать состоящей из последовательно
соединенных активного сопротивления
R и конденсатора С
(рис.
4.14)
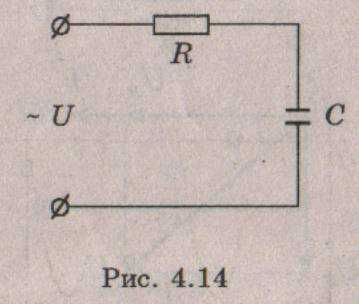
Через
конденсатор и через резистор протекает
один и тот же ток, описываемый формулой
(4.16), поэтому в качестве основного выберем
вектор тока и будем строить вектор
напряжения, приложенного к этой цепи.
Напряжение, приложенное к цепи, равно
векторной сумме падений напряжений на
конденсаторе и на
резисторе:
(4.28)
Напряжение
на резисторе, как было показано выше,
будет совпадать по фазе с током:
(4.29)
а
напряжение на конденсаторе будет
отставать по фазе от тока на угол
?/2:
(4.30)
Построив
векторы
,
и воспользовавшись формулой (4.28), найдем
вектор
.
Векторная диаграмма показана на рис.
4.15.
Из
векторной диаграммы следует, что в
рассматриваемой цепи ток I опережает
по фазе приложенном напряжение,
но
не на ?/ 2, как в случае чистой емкости, а
на некоторый угол
.
Этот угол может принимать значения от
0 до ?
/
2 и при заданной емкости С зависит от
значения активного сопротивления: с
увеличением Rугол
уменьшается.
Рис.
4.15
Как
видно из векторной диаграммы, модуль
вектора
равен
(4.31)
где
величина
(4.32)
называется
полным сопротивлением цепи.
Сдвиг
по фазе
между
током и напряжением данной цепи
определяется из векторной диаграммы:
(4.33)
gigabaza.ru
2.4. Цепь переменного тока с ёмкостным сопротивлением.
Как известно из физики, два проводника, разделённых слоем диэлектрика, образуют электрический конденсатор, обладающий определённой электрической емкостью.
Рассмотрим цепь переменного тока, в которую включен конденсатор емкостью С (рис. 2.8).
Рис. 2.8 Цепь переменного тока с ёмкостной нагрузкой.
К зажимам цепи подведено синусоидальное напряжение, мгновенное значение которого равно (2.14)
Под действием этого напряжения в замкнутой цепи возникает ток, мгновенное значение которого равно:
(2.15)
где q – количество электрических зарядов, измеряемое в кулонах.
Этот ток вызывает падение напряжения между пластинами конденсатора uc. В любой момент времени напряжение между пластинами конденсатора уравновешивает напряжение, приложенное к зажимам цепи, т.е.
(2.16)
Количество электрических зарядов на пластинах конденсатора в любой момент времени определяется по формуле
(2.17)
Подставляя (2.17) и (2.16) в (2.15), получим
(2.18)
Подставляя (2.14) в (2.18), получаем
(2.19)
где — амплитудное значения тока
(2.20)
Разделив обе части уравнения (2.20) на получим, закон Ома для цепи переменного тока с конденсатором.
(2.21)
Рассмотрим размерность знаменателя выражения (2.21)
Обозначим и назовем емкостным сопротивлением конденсатора. Емкостное сопротивление зависит от емкости конденсатора и частоты тока.
Сравнивая между собой выражения (2.14) и (2.19) делаем вывод: в цепи переменного тока с конденсатором напряжение отстаёт от тока по фазе на 90°.
Мгновенная мощность цепи с конденсатором равна
(2.22)
Построим векторную и волновую диаграммы цепи с емкостным сопротивлением (рис. 2.9).
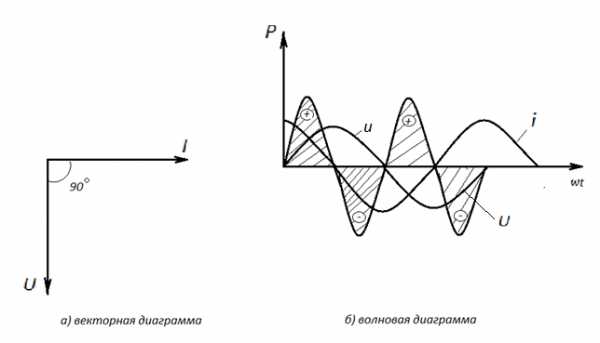
Рис. 2.9 Волновая и векторная диаграммы цепи переменного тока с емкостным сопротивлением.
Из выражения (2.22) и векторной диаграммы видно, что мгновенная мощность в цепи с конденсатором изменяется во времени с удвоенной частотой, по отношению к частоте тока. В течении 1 и 3 четвертей периода при изменении напряжения от нуля до амплитудного значения мощность положительна. Это означает, что энергия посылаемая во внешнюю цепь источником запасается в конденсаторе в виде энергии электрического поля . В течение второй и четвёртой четвертей периода, при изменении напряжения от амплитудного значения до нуля мощность отрицательна. Это означает, что конденсатор возвращает запасенную энергию обратно источнику.
Таким образом в цепи переменного тока с конденсатором происходит периодический обмен энергией между внешним источником и электрическим полем конденсатора. Средняя мощность, потребляемая конденсатором за период, равна нулю, т.е. в такой цепи источник не расходует энергию и, следовательно, в конденсаторе не происходит необратимого преобразования электрической энергии в другие виды энергий.
Мощность цепи с конденсатором оценивается по величине емкостной мощности, измеряемой, как и индуктивная мощность, в вольт-ампер реактивных и характеризующей интенсивность обмена энергией между генератором и электрическим полем конденсатора
[ВАр]
Индуктивная и емкостная мощности называются реактивными мощностями. Емкостная мощность конденсатора не может быть использована в практических целях.
studfiles.net
18.Цепи синусоидального тока с отдельными элементами (активным, индуктивным и емкостным сопротивлением), векторные изображения этих величин.
Простейшие цепи – цепи, содержащие один элемент.
1) Участок цепи, содержащий активное сопротивление (рис. 2.6).
Рис. 2.6
Зададимся изменением тока в резисторе по синусоидальному закону
i(t) = ImR sin(ωt + ψi).
Воспользуемся законом Ома для мгновенных значений тока и напряжения
u(t) = R i(t)
и получим
(2.13)
u(t) = R ImR sin(ωt + ψi).
Формальная запись синусоидального напряжения имеет вид
(2.14)
u(t) = UmR sin(ωt + ψu)
Соотношения (2.13) и (2.14) будут равны если будут выполнены условия равенства амплитуд и фаз
(2.15)
UmR = R ImR,
(2.16)
ψu = ψi.
Соотношение (2.15) может быть записано для действующих значений
(2.17)
UR = R IR.
Соотношение (2.16) показывает, что фазы напряжения и тока в резисторе совпадают. Графически это представлено на временной диаграмме (рис. 2.7) и на комплексной плоскости (рис. 2.8).
Рис. 2.7 и 2.8
2) Участок цепи, содержащий идеальную индуктивность (рис 2.9)
Рис. 2.9
Зададим изменение тока в индуктивности по синусоидальному закону
i(t) = ImL sin(ωt + ψi).
Используем уравнение связи между током и напряжением в индуктивности
uL = L · di / dt
и получим
uL(t) = ωL · ImL cos(ωt + ψi).
Заменим cos на sin и получим
(2.18)
uL(t) = ωL · ImL sin(ωt + ψi + 90°).
Формальная запись синусоидального напряжения имеет вид
(2.19)
uL(t) = UmL sin(ωt + ψu).
Соотношения (2.18) и (2.19) будут равны если выполняется условие равенства амплитуд и фаз
(2.20)
UmL = ωL · ImL,
(2.21)
ψu = ψi + 90°.
Уравнение (2.20) можно переписать для действующих значений
(2.22)
UL = ωL · IL.
Уравнение (2.21) показывает, что фаза тока в индуктивности отстает от фазы напряжения на 90°. Величину XL = ωL в уравнении (2.20) называют индуктивным сопротивлением. Единицей его измерения является Ом. Графически электрические процессы в индуктивности представлены на рис. 2.10, 2.11.
Рис. 2.10 и 2.11
3) Участок цепи, содержащий ёмкость (рис. 2.12)
Рис. 2.12
Зададим изменение тока в емкости по синусоидальному закону
i(t) = ImC sin(ωt + ψi).
Используем уравнением связи между током и напряжением в емкости
uC = 1 / C · ∫ i dt,
и получим
uC = 1 / (ωC) · ImC (-cos(ωt + ψi)).
Заменим –cos на sin
(2.23)
uC = 1 / (ωC) · ImC sin(ωt + ψi — 90°).
Формальная запись синусоидального напряжения имеет вид
(2.24)
uC = UmC sin(ωt + ψu).
Соотношения (2.23) и (2.24) будут равны если выполняется условие равенства амплитуд и фаз
(2.25)
UmC = 1 / (ωC) · ImC,
(2.26)
ψu = ψi — 90°.
Уравнение (2.25) можно переписать для действующих значений
(2.27)
UC = 1 / (ωC) · IC.
Уравнение (2.26) показывает, что фаза напряжения в емкости отстает от фазы тока на 90°. Величину XC = 1 / (ωC) в уравнении (2.25) называют емкостным сопротивлением цепи и измеряют его в Омах. Графически электрические процессы в емкости представлены на рис. 2.13, 2.14.
19. Последовательное соединение активного и индуктивного сопротивления. Реальная и идеальная катушка индуктивности.
Рисунок последовательного соединения активного и индуктивного сопротивления.
Векторная диаграмма для этого соединения.
Рисунок треугольника сопротивлений при последовательном соединении активного и индуктивного сопротивления.
Формула:
Где: Z — полное сопротивление цепи (Ом)
R — активное сопротивление цепи (Ом)
XL — индуктивное сопротивление цепи (Ом).
Идеальная катушка индуктивности – это элемент электрической цепи, запасающий электрическую энергию в магнитном поле, которую может полностью возвратить в последующем. Поэтому идеальная катушка индуктивности активную энергию не потребляет, и её активная мощность равна нулю. (P = 0 — для идеальной катушки).
Математическая модель идеальной катушки индуктивности отражает то, что приложенное к ней напряжение uL уравновешивается ЭДС самоиндукции e.
uL = – e = L ,где L –индуктивность катушки,измеряемая в Генри (Гн).
На переменном токе катушка обладает индуктивным сопротивлением: XL = ωL = 2πfL
Реальная катушка отличается от идеальной тем, что переменный ток в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид.
В цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью. В реальной катушке имеют место оба процесса, т.е. ее активная и реактивная мощности отличны от нуля. Поэтому в схеме замещения реальная катушка должна быть представлена активным и реактивным элементами.
studfiles.net